简介
判断点与多边形位置关系算法是几何算法中最基础的算法之一,包括布尔运算在内的非常非常多的算法都会用到它。它的稳定是算法库稳定的关键。
下面我们从一个边都是直线的多边形开始了解射线法的原理。然后看看引入曲线后会带来哪些问题,以及在实际应用还有哪些其他问题。最后看看如何实现一个稳定的,支持曲线边多边形的点与多边形位置关系算法。
射线法
讲射线法的资料很多,用AI也能轻松查到详细内容,所以我们只简单介绍一下重点,为后面内容做个铺垫。
射线法的实现思路是以被检测点为起点做一条射线,看和多边形有几个交点,奇数个交点说明在内部,偶数个交点说明在外部(0算偶数)。
实际中往往以x轴正方向做射线,这样计算比较简单。
交点计数时,要考虑各种相交类型,例如射线和边重合,射线过顶点等。
有一个已经总结好的的原则可以直接使用(以x轴正方向射线为例):
当边的一个顶点的y大于参考点的y,另一个顶点的y不大于参考点的y(等于或小于),且边与x轴交点的x大于参考点的x时计数加一。
如何判断点是否在多边形上呢?因为一般这个判断都需要带一个精度,所以直接用上面介绍方法中的得到的边与x轴交点到参考点x的距离是不准确的。
我见过两种方式:
一种是单独判断点是否在边上。
另一种是点加上精度会得到一个Box,用这个Box的顶点分别做射线法,如果有些顶点为内部,有些顶点为外部则认为是点在多边形上边。
两种方法适用的是不同的场景,大家按需选择。
曲线边给基础射线法稳定性带来的挑战
首先曲线与射线相交可能会有多个交点,我们就不能只拿曲线的两个端点来判断了,而是要根据交点位置曲线是否穿过射线来判断是否计数加一。
是否穿过一般用交点处的切线方向来判断。但如果曲线和切线相切时,就需要根据二阶导数甚至更高阶导数来判断穿过关系了。
但相切本身就是个带精度判断的问题。一阶导数小于多少用二阶导数,二阶导数小于多少用三阶导数。这个没有唯一的结论。一个场景对了,另一个场景可能就不对了。
另外,相切时,因为精度的问题,我们几乎不可能计算到恰巧相切的点。不是偏左点就是偏右点,甚至参数域上偏很多都有可能。如果曲线曲率很大,这个偏差也可能对切线方向带来比较大的影响,从而影响稳定性。
还有就是,边都是直线时,我们可以保证各边之间无缝连接。是曲线时就很难保证无缝连接了。原因是因为曲线的表示方式导致的。
例如画图时我们用三点定义圆弧,但圆弧在内存中存储时用圆心半径和角度。那么我们根据三点计算出的圆心半径和角度再反算回三点时,在特殊场景中是存在误差的。这个误差就会导致边连接处存在一个小小的缝隙,这个小小的缝隙出现在射线附近时就有可能导致错误。
有些算法库,多边形是其他运算的结果(例如布尔运算),本身可能就带符合误差要求的缝隙(因为有可能基于效率原因考虑不做缝隙修复)。
上面提到的情况绝对不是危言耸听,都是我们在实际项目中碰到过的。算法本身不难,难的是如何在各种场景下都能表现的稳定。
为了给大家对上面说的有个更直观的认识,我画了个草图放到下面。

稳定的射线法
基于前面的讨论,相切或接近相切时,从理论上就是不能解决的。
一个最简单的解决思路是,检测上述情况,发现出现了就再换一条射线。
从概率上,这种算法没问题。但多边形复杂时,有可能需要换好几次射线才能得出结果。另外,如果射线不是x轴或y轴方向时,直线和曲线求交的效率也会下降。
下面介绍一下我们设计的算法思路。
-
y轴正方向做射线,计算所有交点。
-
根据交点统计计数和可信度,可信度符合要求则直接返回结果。
-
如果多边形有顺逆时针方向,根据第一个交点的穿过形式和可信度判断内外,可信度满足要求直接返回结果。
-
y轴负方向做射线,计算所有交点。
-
根据交点统计计数和可信度,可信度符合要求则直接返回结果。
-
如果多边形有顺逆时针方向,根据第一个交点的穿过形式和可信度判断内外,可信度满足要求直接返回结果。
-
利用交点把多边形打断成片段,这些片段是被y轴正负方向射线分开的。
-
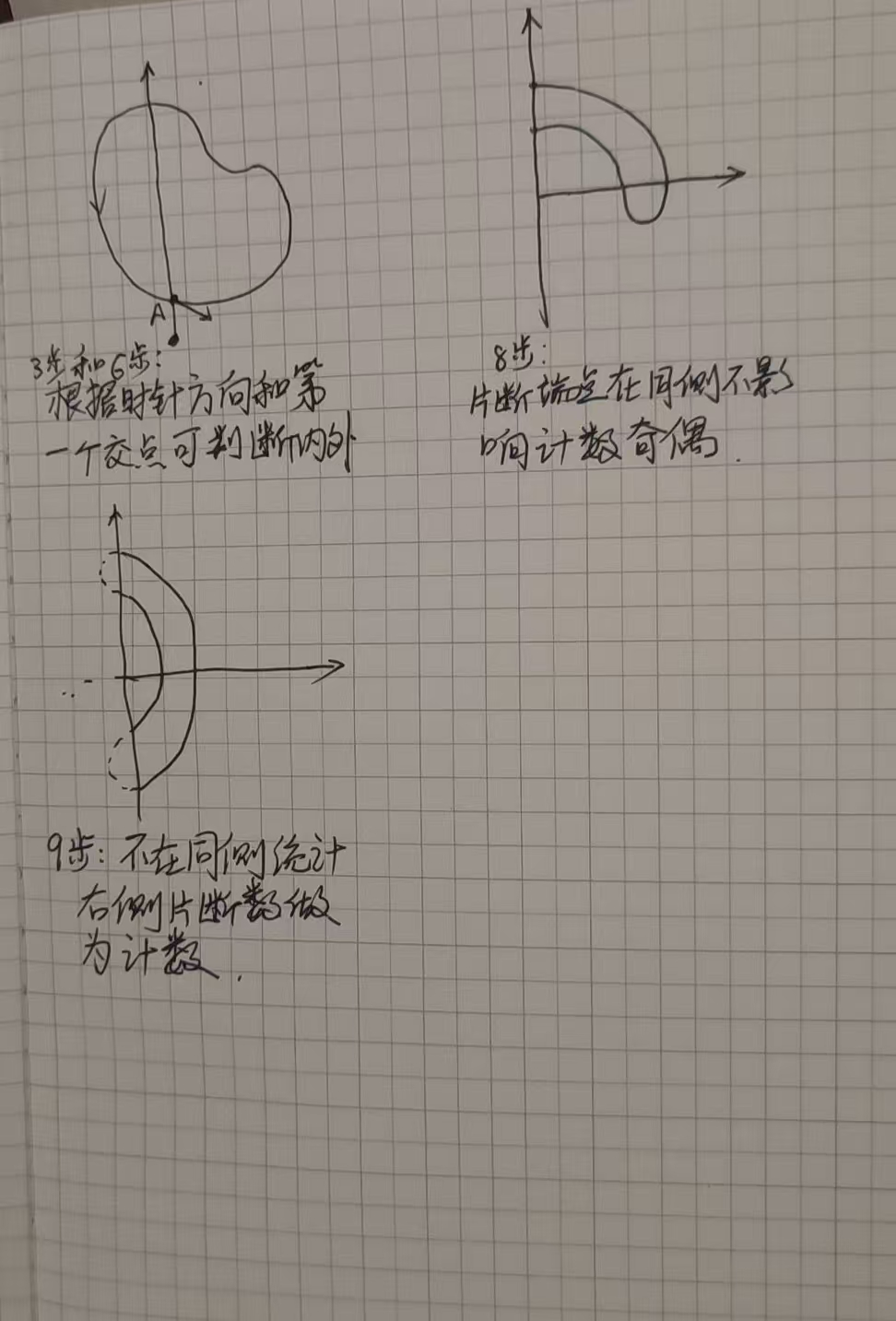
判断片段的两个端点是否在x轴方向射线同侧,如果在同侧不影响计数,直接不用考虑。
-
如果不在同侧,统计在y轴正方向射线的右侧片段数,这个片段数就是判断内外的计数。这步可以通过采用的方式判断是否在右侧。
如下图所示:
总结
这可能就是书本中的算法和在大厂中实际跑的算法的区别。书本中的算法追求理论可行,实际应用的算法追求实践可行。
虽然我以前写过好多版这个算法了,但为了写这篇文章,我又把它实现了一遍,源码放到星球里了。为了省时间目前只做了直线求交,但算法本身是支持曲线的。
星球中的Demo可直接调试运行,学源码能看到很多细节,欢迎加入我们的星球,支持一下作者。**现有源码已经很值得加入了。**后续算法源码还会不断在星球中发布。
