信奥赛C++提高组csp-s之拓扑排序详解

一、拓扑排序基本概念
拓扑排序(Topological Sort)是对有向无环图(DAG)的一种线性排序,使得对于图中的每一条有向边(u, v),u在排序中总是位于v的前面。
基本性质:
- 只有有向无环图(DAG)才有拓扑排序
- 一个DAG可能有多个拓扑排序结果
- 拓扑排序不唯一
二、拓扑排序算法实现
Kahn算法(基于入度)
算法步骤:
-
计算所有节点的入度
-
将所有入度为0的节点加入队列
-
当队列不为空时:
- 取出队首节点u,加入结果
- 移除u的所有出边,即u的邻接节点v的入度减1
- 如果v的入度变为0,将v加入队列
-
如果结果包含所有节点,则成功;否则图中存在环
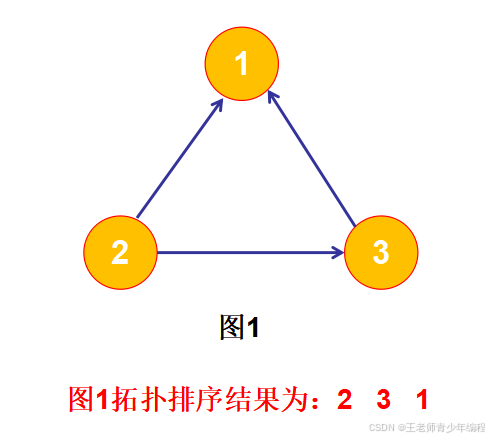

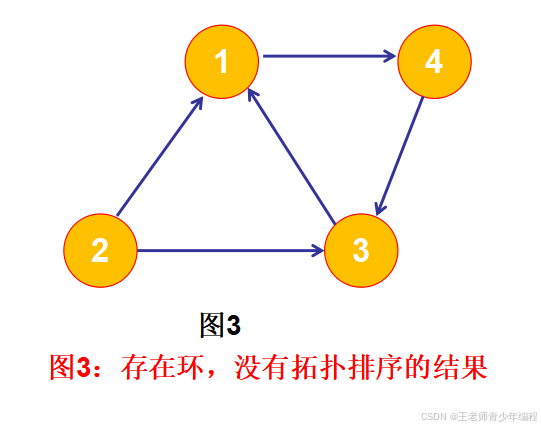
三、研究案例:判环
题目描述
一个图,有n个节点,及m条有向边,判断该图是否有环。
输入格式
第一行两个整数n和m,表示节点数和边数。
接下来m行,每行两个整数u和v,表示一条有向边从u指向v(节点编号从1开始,或者0开始,这里我们假设从1开始)。
输出格式
如果存在环,输出"存在环",否则输出拓扑排序的结果(任意一种即可)。
数据规模
- 节点数:1 ≤ n ≤ 10 5 10^5 105
- 边数:0 ≤ m ≤ 10 5 10^5 105
输入输出样例
样例1:无环图
输入:
5 5
1 2
1 3
2 4
3 4
4 5输出:
1 2 3 4 5 样例2:有环图
输入:
3 3
1 2
2 3
3 1输出:
存在环代码实现:
cpp
#include<bits/stdc++.h>
using namespace std;
int n, m; // n: 节点数, m: 边数
int main() {
// 输入节点数和边数
cin >> n >> m;
// 邻接表存储图结构,g[i]存储节点i指向的所有节点
vector<vector<int>> g(n + 1);
// 入度统计数组,d[i]表示节点i的入度(指向该节点的边数)
vector<int> d(n + 1, 0);
// 读入所有边并构建图
for (int i = 1; i <= m; i++) {
int u, v;
cin >> u >> v; // 读入一条从u到v的有向边
g[u].push_back(v); // 将v添加到u的邻接表中
d[v]++; // v节点的入度增加
}
queue<int> q; // 用于拓扑排序的队列(存储当前入度为0的节点)
vector<int> topo; // 存储拓扑排序结果
// 将所有初始入度为0的节点加入队列
for (int i = 1; i <= n; i++) {
if (d[i] == 0) {
q.push(i);
}
}
// 拓扑排序核心过程(Kahn算法)
while (!q.empty()) {
int u = q.front(); // 取出一个入度为0的节点
q.pop();
topo.push_back(u); // 加入拓扑序列
// 遍历当前节点的所有后继节点
for (int v : g[u]) {
d[v]--; // 移除u->v边,v的入度减1
if (d[v] == 0) { // 如果v的入度变为0
q.push(v); // 将v加入队列
}
}
}
// 判断是否存在环
if (topo.size() != n) {
// 拓扑序列长度不足n,说明存在环
cout << "存在环";
} else {
// 输出拓扑排序结果
for (int node : topo) {
cout << node << " ";
}
}
return 0;
}功能分析:
该程序实现了有向图环检测与拓扑排序 功能,使用经典的Kahn算法:
-
图表示与初始化:
- 使用邻接表
g存储图结构(空间效率高,适合稀疏图) - 使用入度数组
d记录每个节点的入度值
- 使用邻接表
-
拓扑排序过程:
- 初始化:将所有入度为0的节点加入队列
- 循环处理 :
- 从队列取出节点加入拓扑序列
- 将该节点的所有后继节点入度减1
- 若减1后入度变为0,则加入队列
- 终止条件:队列为空
-
环检测:
- 拓扑序列长度 = n → 无环,输出拓扑序列
- 拓扑序列长度 < n → 存在环(剩余节点形成环)
-
算法特性:
- 时间复杂度:O(n+m)(每个节点和边各处理一次)
- 空间复杂度:O(n+m)(存储图结构和辅助数据结构)
- 结果特性:拓扑排序结果不唯一(与入度为0节点的处理顺序有关)
算法原理图解:
样例1:无环图 (5节点)
1 → 2 → 4 → 5
1 → 3 → 4
入度初始化:
节点: 1 2 3 4 5
入度: 0 1 1 2 1
处理过程:
1. 节点1入度0 → 加入队列
2. 处理节点1 → 2、3入度减1 → 2入度0入队,3入度0入队
3. 处理节点2 → 4入度减1(1) → 不入队
4. 处理节点3 → 4入度减1(0) → 入队
5. 处理节点4 → 5入度减1(0) → 入队
6. 处理节点5
结果: [1,2,3,4,5](或[1,3,2,4,5])
样例2:有环图 (3节点)
1 → 2 → 3 → 1
入度初始化:
节点: 1 2 3
入度: 1 1 1
处理过程:
所有节点入度>0 → 队列始终为空
拓扑序列长度0 ≠ 3 → 存在环四、拓扑排序常见应用场景
- 任务调度:确定任务执行的先后顺序
- 课程安排:解决课程先修关系问题
- 依赖解析:如软件包依赖、编译顺序等
- 死锁检测:通过检测环来判断系统是否会出现死锁
- 关键路径:在AOE网中计算关键路径
各种学习资料,助力大家一站式学习和提升!!!
cpp
#include<bits/stdc++.h>
using namespace std;
int main(){
cout<<"########## 一站式掌握信奥赛知识! ##########";
cout<<"############# 冲刺信奥赛拿奖! #############";
cout<<"###### 课程购买后永久学习,不受限制! ######";
return 0;
}- 一、CSP信奥赛C++通关学习视频课:
- C++语法基础
- C++语法进阶
- C++算法
- C++数据结构
- CSP信奥赛数学
- CSP信奥赛STL
- 二、CSP信奥赛C++竞赛拿奖视频课:
- 信奥赛csp-j初赛高频考点解析
- CSP信奥赛C++复赛集训课(12大高频考点专题集训)
- 三、csp高频考点知识详解及案例实践:
- CSP信奥赛C++之动态规划
- CSP信奥赛C++之标准模板库STL
- 信奥赛C++提高组csp-s知识详解及案例实践
- 四、考级、竞赛刷题题单及题解:
- GESP C++考级真题题解
- CSP信奥赛C++初赛及复赛高频考点真题解析
- CSP信奥赛C++一等奖通关刷题题单及题解
详细内容:
1、csp/信奥赛C++,完整信奥赛系列课程(永久学习):
https://edu.csdn.net/lecturer/7901 点击跳转



2、CSP信奥赛C++竞赛拿奖视频课:
https://edu.csdn.net/course/detail/40437 点击跳转

3、csp信奥赛高频考点知识详解及案例实践:
CSP信奥赛C++动态规划:
https://blog.csdn.net/weixin_66461496/category_13096895.html点击跳转
CSP信奥赛C++标准模板库STL:
https://blog.csdn.net/weixin_66461496/category_13108077.html 点击跳转
信奥赛C++提高组csp-s知识详解及案例实践:
https://blog.csdn.net/weixin_66461496/category_13113932.html
4、csp信奥赛冲刺一等奖有效刷题题解:
CSP信奥赛C++初赛及复赛高频考点真题解析(持续更新):https://blog.csdn.net/weixin_66461496/category_12808781.html 点击跳转
CSP信奥赛C++一等奖通关刷题题单及题解(持续更新):https://blog.csdn.net/weixin_66461496/category_12673810.html 点击跳转
5、GESP C++考级真题题解:

GESP(C++ 一级+二级+三级)真题题解(持续更新):https://blog.csdn.net/weixin_66461496/category_12858102.html 点击跳转

GESP(C++ 四级+五级+六级)真题题解(持续更新):https://blog.csdn.net/weixin_66461496/category_12869848.html 点击跳转
· 文末祝福 ·
cpp
#include<bits/stdc++.h>
using namespace std;
int main(){
cout<<"跟着王老师一起学习信奥赛C++";
cout<<" 成就更好的自己! ";
cout<<" csp信奥赛一等奖属于你! ";
return 0;
}