第十四届蓝桥杯青少组C++选拔赛[2023.2.12]第二部分编程题（5、机甲战士）

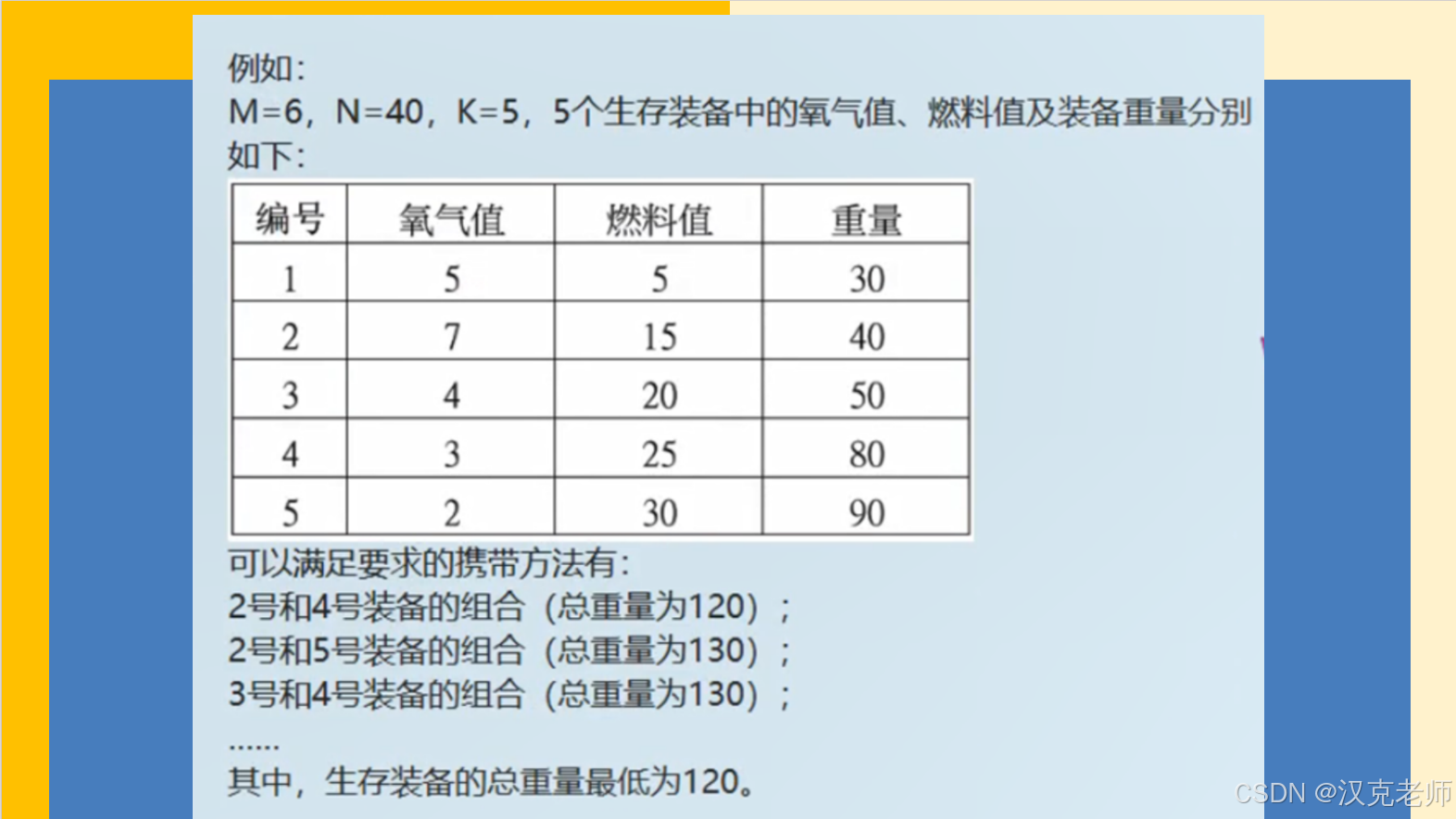
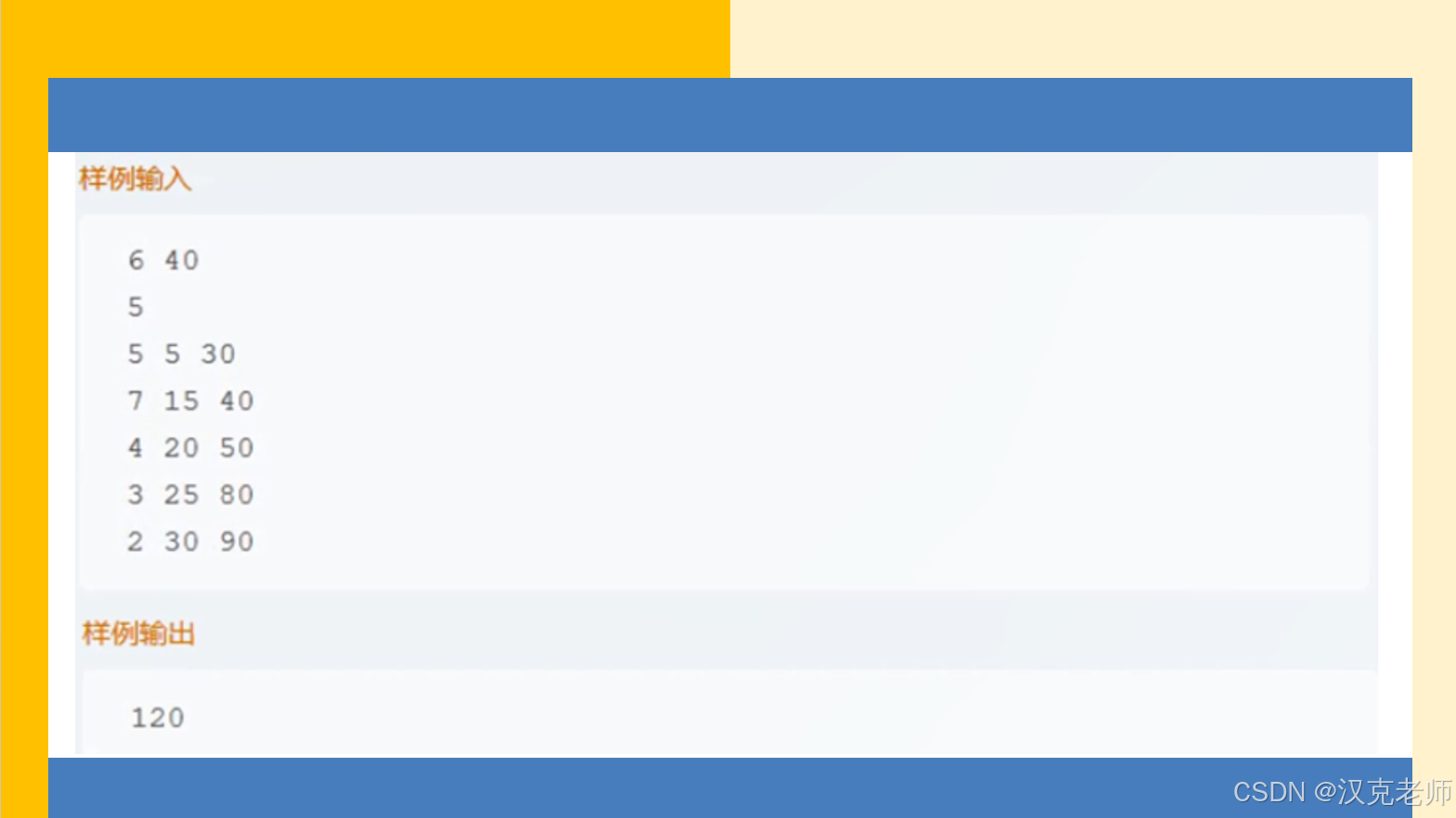
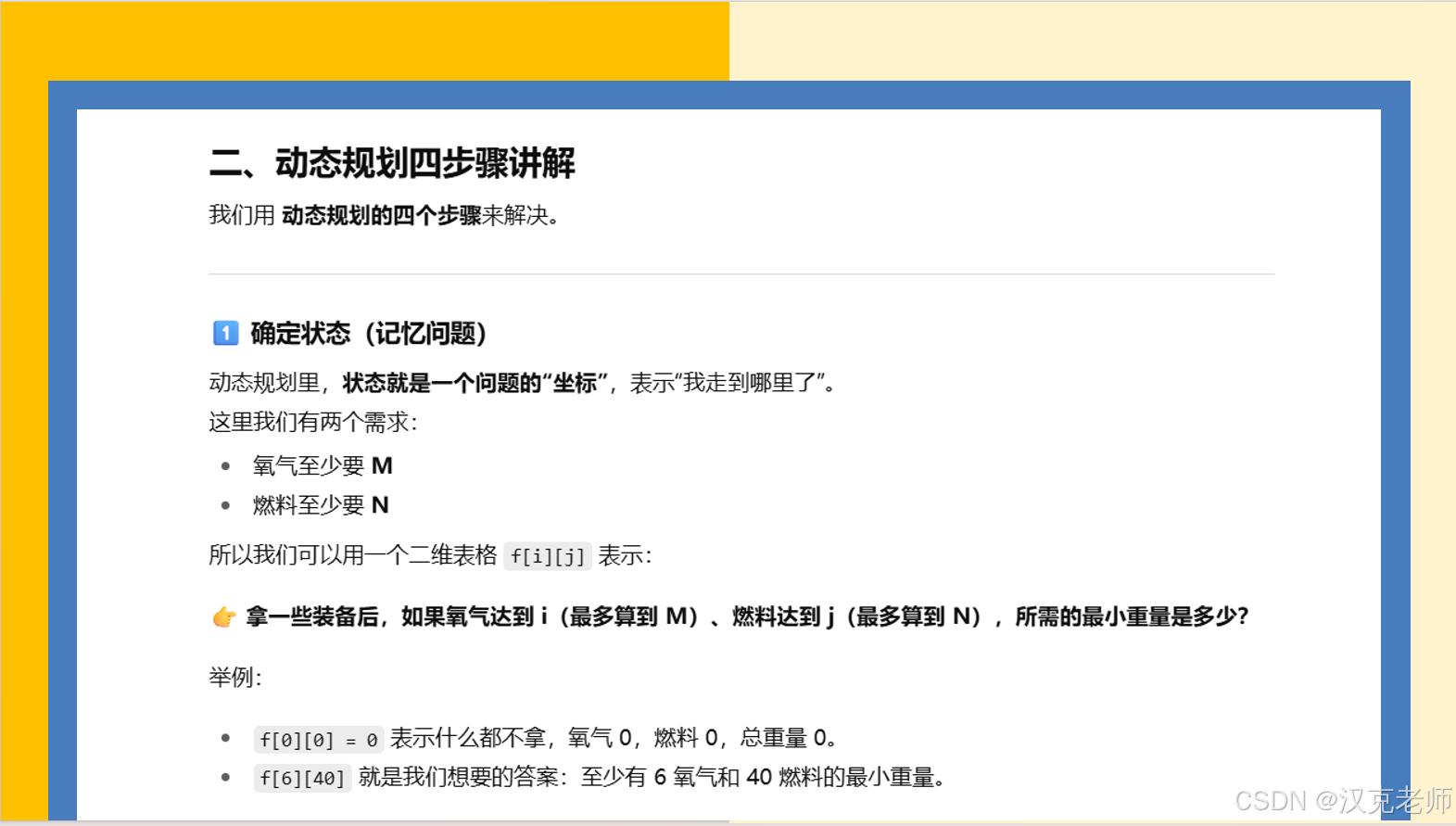
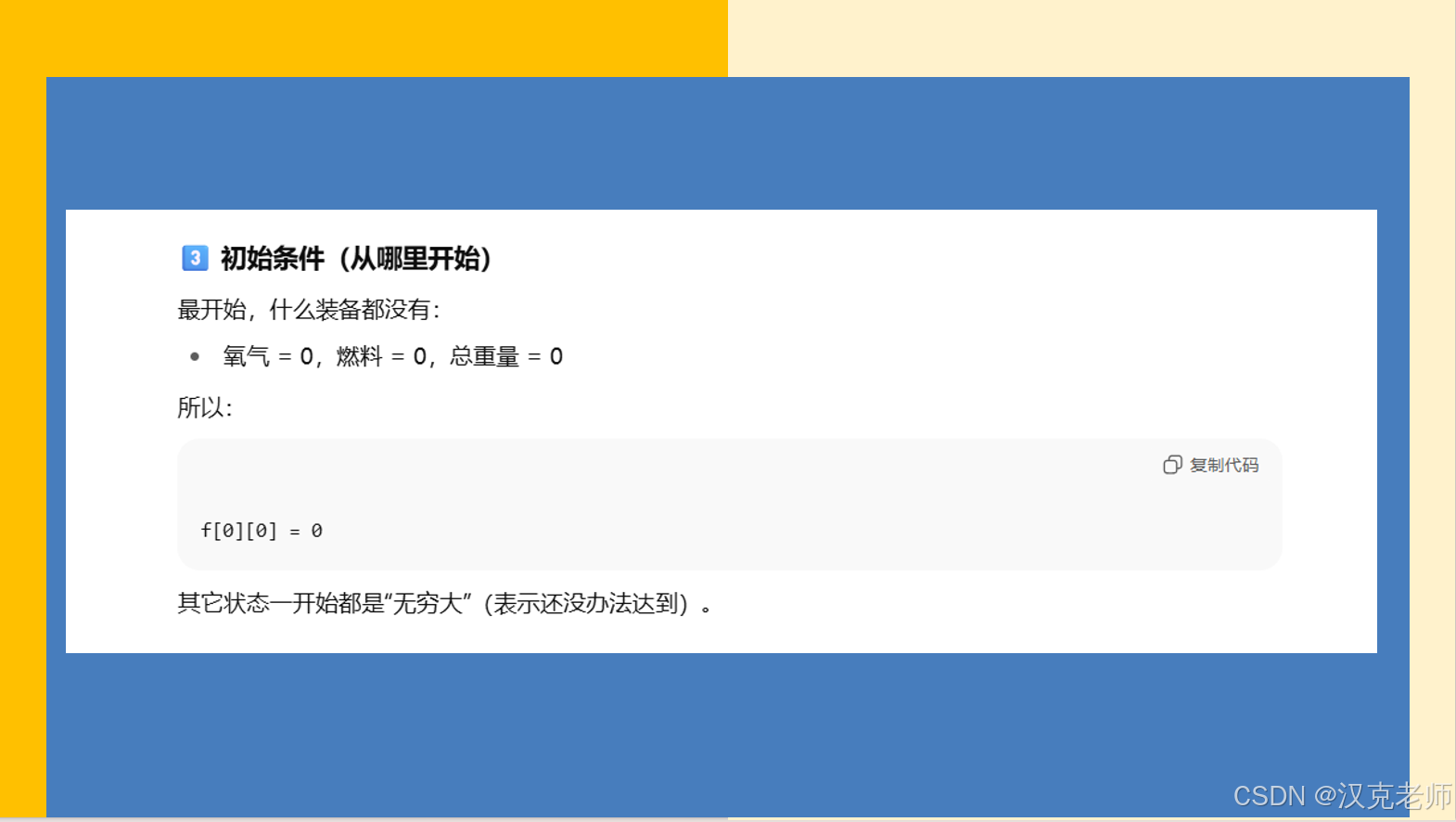
参考程序：

#include<iostream>
#include<algorithm>
using namespace std;

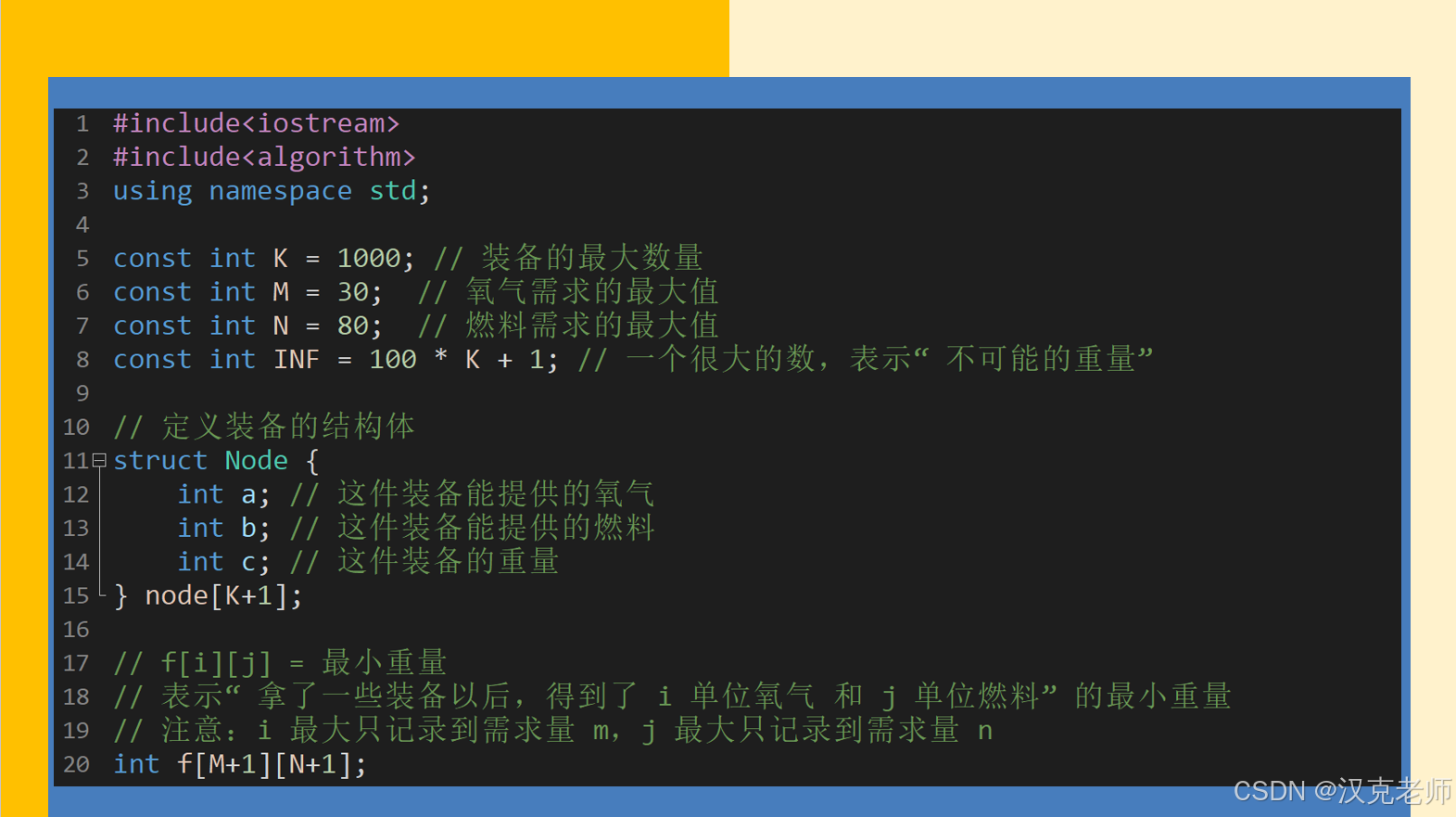
const int K = 1000; // 装备的最大数量
const int M = 30;  // 氧气需求的最大值
const int N = 80;  // 燃料需求的最大值
const int INF = 100 * K + 1; // 一个很大的数，表示"不可能的重量"

// 定义装备的结构体
struct Node {
    int a; // 这件装备能提供的氧气
    int b; // 这件装备能提供的燃料
    int c; // 这件装备的重量
} node[K+1];

// f[i][j] = 最小重量
// 表示"拿了一些装备以后，得到了 i 单位氧气 和 j 单位燃料"的最小重量
// 注意：i 最大只记录到需求量 m，j 最大只记录到需求量 n
int f[M+1][N+1];

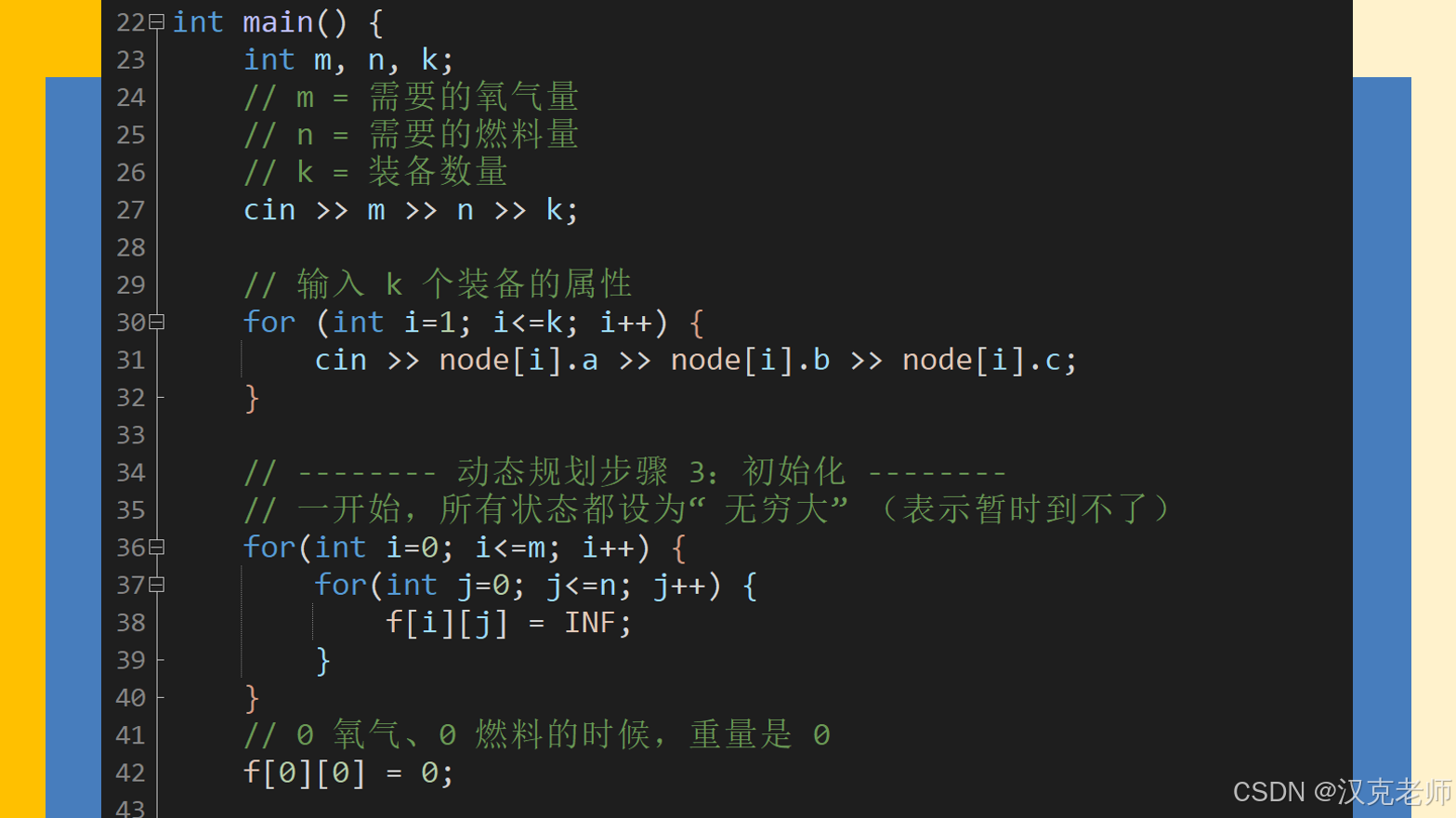
int main() {
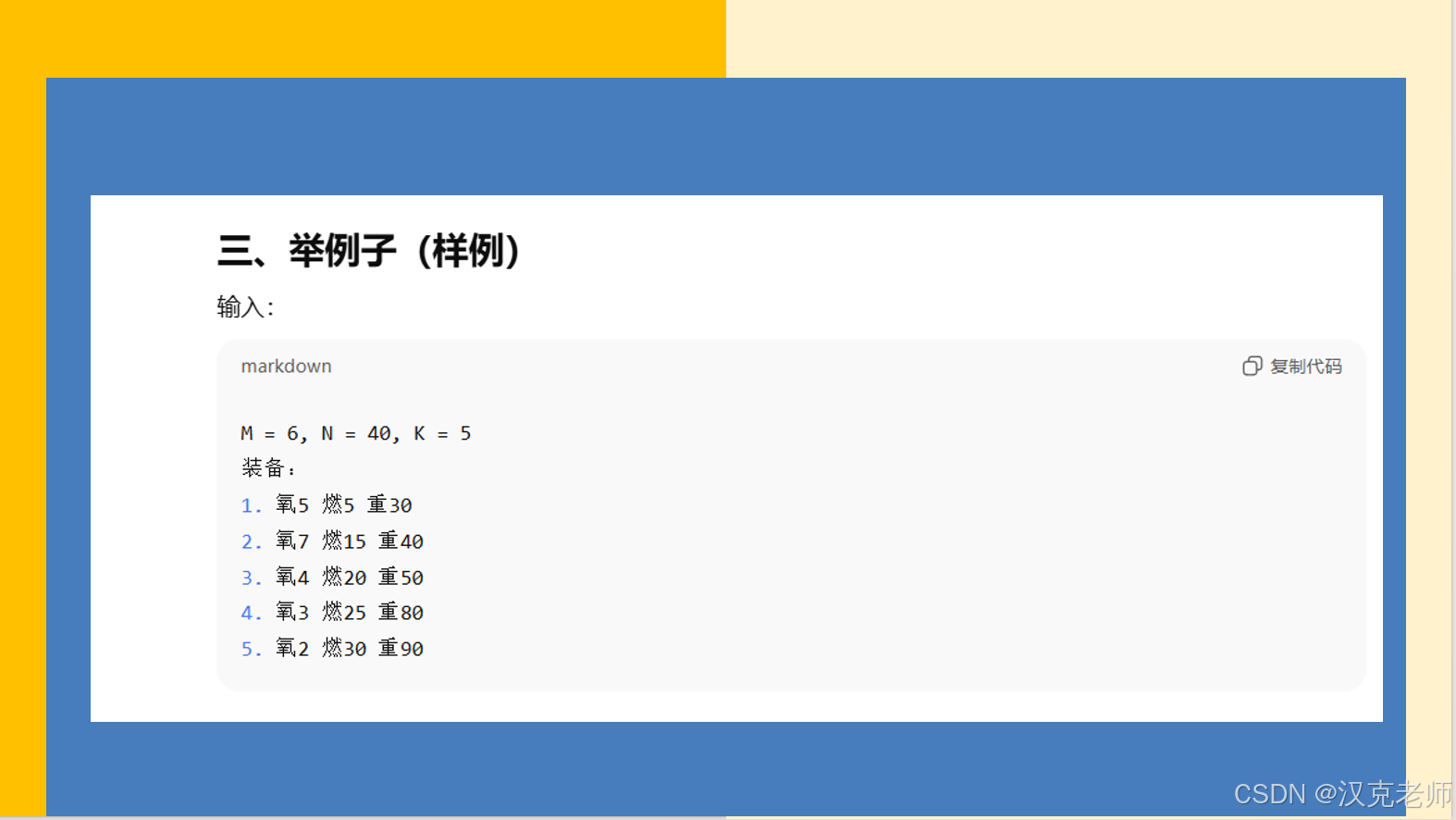
    int m, n, k; 
    // m = 需要的氧气量
    // n = 需要的燃料量
    // k = 装备数量
    cin >> m >> n >> k;

    // 输入 k 个装备的属性
    for (int i=1; i<=k; i++) {
        cin >> node[i].a >> node[i].b >> node[i].c;
    }

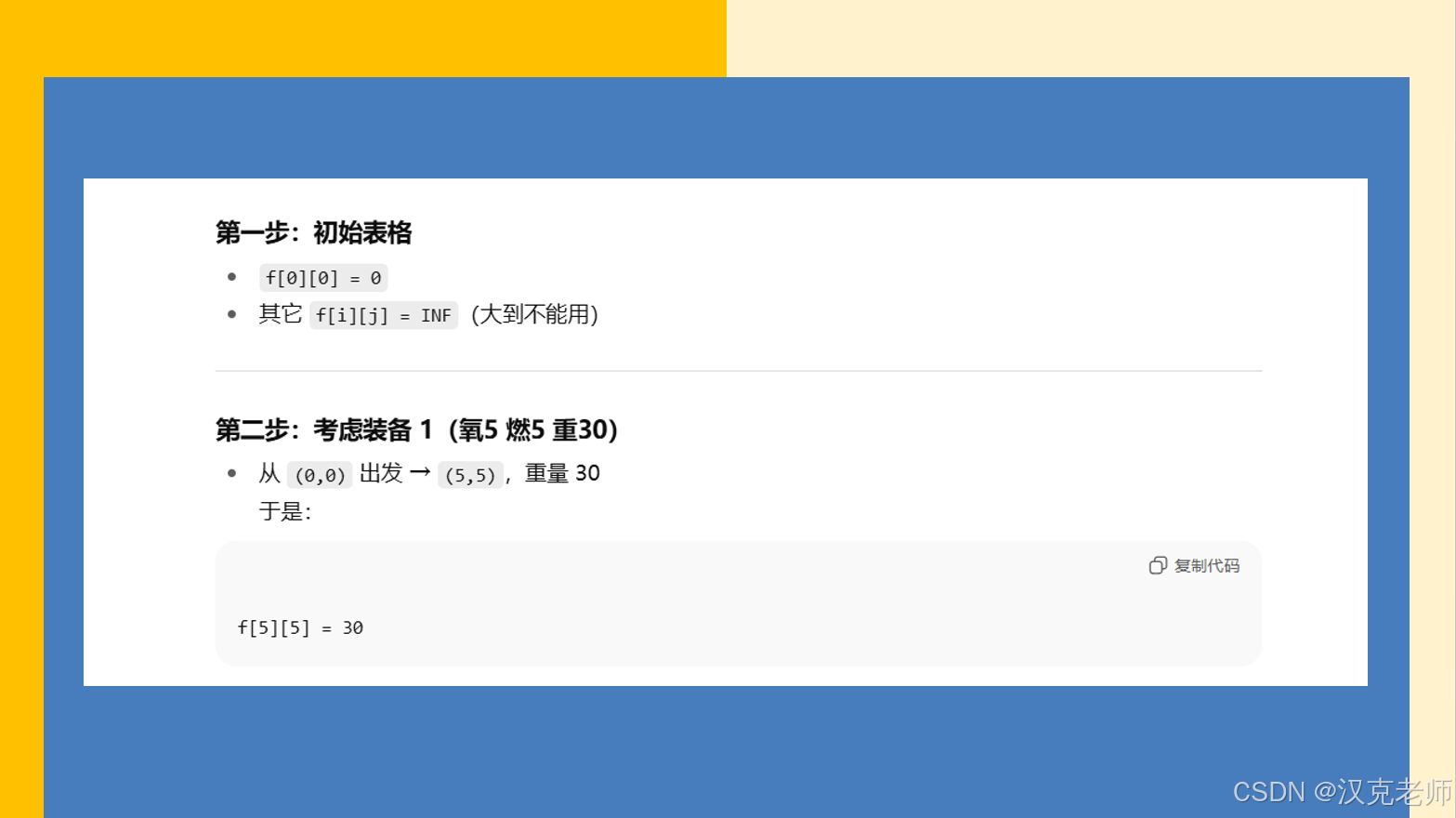
    // -------- 动态规划步骤 3：初始化 --------
    // 一开始，所有状态都设为"无穷大"（表示暂时到不了）
    for(int i=0; i<=m; i++) {
        for(int j=0; j<=n; j++) {
            f[i][j] = INF;
        }
    }
    // 0 氧气、0 燃料的时候，重量是 0
    f[0][0] = 0;

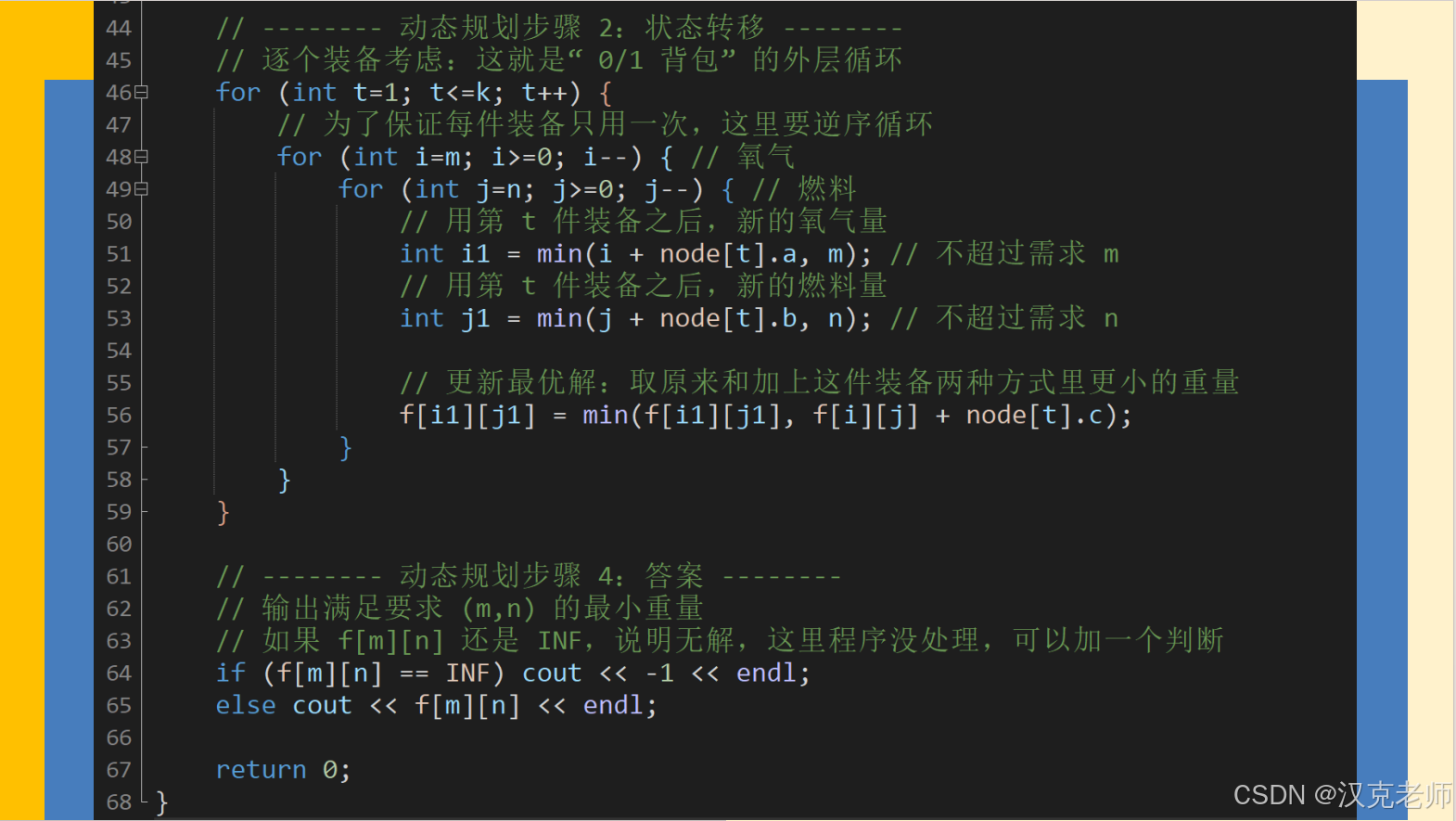
    // -------- 动态规划步骤 2：状态转移 --------
    // 逐个装备考虑：这就是"0/1 背包"的外层循环
    for (int t=1; t<=k; t++) {
        // 为了保证每件装备只用一次，这里要逆序循环
        for (int i=m; i>=0; i--) { // 氧气
            for (int j=n; j>=0; j--) { // 燃料
                // 用第 t 件装备之后，新的氧气量
                int i1 = min(i + node[t].a, m); // 不超过需求 m
                // 用第 t 件装备之后，新的燃料量
                int j1 = min(j + node[t].b, n); // 不超过需求 n

                // 更新最优解：取原来和加上这件装备两种方式里更小的重量
                f[i1][j1] = min(f[i1][j1], f[i][j] + node[t].c);
            }
        }
    }

    // -------- 动态规划步骤 4：答案 --------
    // 输出满足要求 (m,n) 的最小重量
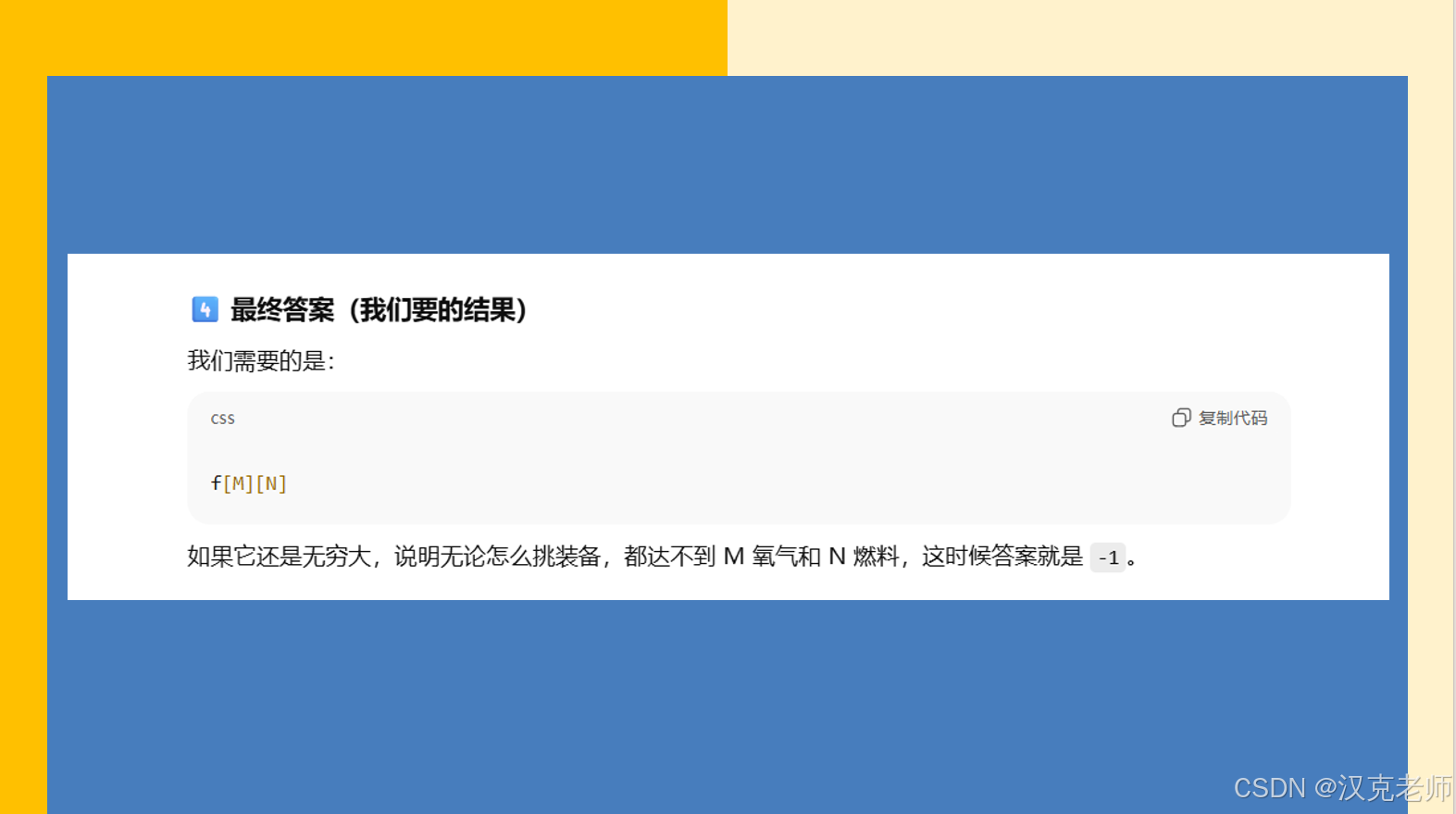
    // 如果 f[m][n] 还是 INF，说明无解，这里程序没处理，可以加一个判断
    if (f[m][n] == INF) cout << -1 << endl;
    else cout << f[m][n] << endl;

    return 0;
}