【LeetCode刷题】杨辉三角

给定一个非负整数 numRows， 生成「杨辉三角」的前 *numRows*行。

在**「杨辉三角」**中，每个数是它左上方和右上方的数的和。

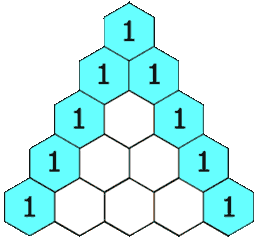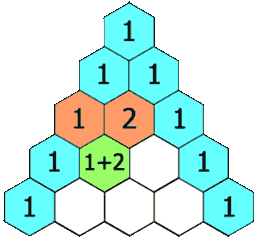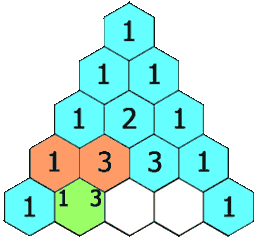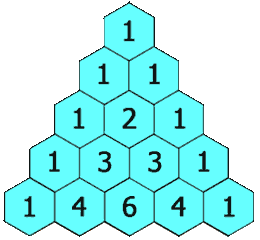
示例 1:

复制代码

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2:

复制代码

输入: numRows = 1
输出: [[1]]

提示:

1 <= numRows <= 30

算法思路：

初始化与边界处理 ：若numRows=0，直接返回空列表；否则先将第一行[1]加入结果列表。
逐行构建：
- 对于第i行（从第 2 行开始），先获取上一行prev_row；
- 当前行的首尾元素固定为1；
- 中间元素通过遍历上一行的索引1到len(prev_row)-1，计算prev_row[j-1] + prev_row[j]得到。
结果返回 ：循环结束后，result中存储了杨辉三角的前numRows行，直接返回即可。

Python代码：

python 复制代码

from typing import List


class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        """
        生成杨辉三角的前numRows行
        :param numRows: 要生成的行数，非负整数
        :return: 二维列表，每个子列表对应杨辉三角的一行
        """
        # 初始化结果列表，用于存储最终的杨辉三角
        result = []

        # 边界条件1：如果要求生成0行，直接返回空列表
        if numRows == 0:
            return result

        # 边界条件2：第一行固定为[1]，先加入结果列表
        result.append([1])

        # 从第2行开始循环构建（i表示当前行的索引，从1到numRows-1）
        for i in range(1, numRows):
            # 获取上一行的元素，用于计算当前行
            prev_row = result[i - 1]
            # 初始化当前行，第一个元素固定为1
            current_row = [1]

            # 填充当前行的中间元素（j从1到上一行长度-1）
            # 中间元素 = 上一行第j-1个元素 + 上一行第j个元素
            for j in range(1, len(prev_row)):
                current_row.append(prev_row[j - 1] + prev_row[j])

            # 当前行最后一个元素固定为1
            current_row.append(1)

            # 将当前行加入结果列表
            result.append(current_row)

        return result


# 本地测试用例（直接运行代码即可验证）
if __name__ == "__main__":
    solution = Solution()
    # 测试示例1：生成5行杨辉三角
    print("生成5行杨辉三角：")
    print(solution.generate(5))  # 预期输出：[[1], [1,1], [1,2,1], [1,3,3,1], [1,4,6,4,1]]

    # 测试示例2：生成1行杨辉三角
    print("\n生成1行杨辉三角：")
    print(solution.generate(1))  # 预期输出：[[1]]

    # 测试示例3：生成0行杨辉三角
    print("\n生成0行杨辉三角：")
    print(solution.generate(0))  # 预期输出：[]

LeetCode提交代码：

python 复制代码

class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        # 存储杨辉三角的结果列表
        result = []
        # 处理numRows为0的情况
        if numRows == 0:
            return result
        
        # 第一行固定为[1]
        result.append([1])
        
        # 从第2行开始构建（索引从1到numRows-1）
        for i in range(1, numRows):
            # 获取上一行的元素
            prev_row = result[i-1]
            # 当前行的第一个元素固定为1
            current_row = [1]
            
            # 填充中间元素：等于上一行对应位置的左上方+右上方元素
            for j in range(1, len(prev_row)):
                current_row.append(prev_row[j-1] + prev_row[j])
            
            # 当前行的最后一个元素固定为1
            current_row.append(1)
            
            # 将当前行加入结果列表
            result.append(current_row)
        
        return result

程序运行截图展示：

总结

该算法用于生成杨辉三角的前numRows行。杨辉三角的每个数是其左上方和右上方数的和。算法步骤包括：

（1）初始化结果列表，处理numRows=0的边界情况；

（2）首行固定为[1]；

（3）从第2行开始逐行构建，每行的首尾元素为1，中间元素通过上一行相邻元素相加得到。

时间复杂度为O(numRows²)，空间复杂度为O(1)（不考虑输出存储）。Python实现通过双层循环完成，适用于1≤numRows≤30的输入。测试验证了5行、1行及0行的输出正确性。