1 正运动学分析简介
对于机器人系统,驱动关节及其联动机构是运动系统的重要组成部分。通过对各个关节进行运动控制,可以使机器人或其执行器沿着各种轨迹运动或进行复杂精密的操作。因此,对机器人进行运动学分析显得尤为必要。
机器人运动学主要关注机器人的运动情况及其位姿,而不考虑引起这些运动的力和力矩。其中,有一种机器人运动学问题是:对于一个给定的机器人,已知各个杆件的几何参数和关节变量,求机器人末端执行器相对于参考坐标系的位置和姿态。这个问题,描述的就是机器人正运动学问题,即给定杆件几何参数和关节变量求解末端执行器的位姿。
正运动学分析通过建立关节变量与末端执行器位姿的数学映射关系,为机器人提供精确的运动学模型。例如,采用Denavit-Hartenberg(DH)法构建连杆坐标系,并结合各连杆参数与关节变量的几何关系,为后续设计提供理论框架。这一模型是机器人结构设计、运动仿真及控制算法开发的底层支撑。
具体到机器人系统的设计与开发上,通过正运动学分析还可以计算其他性能指标或验证机构设计合理性。比如对机械臂进行正运动学分析可以计算其工作空间,即通过给定连杆参数和关节变量范围计算机械臂末端执行器的运动范围或在空间中可达到的所有位置点的集合。进一步验证关节配置和连杆参数是否满足任务需求(如覆盖目标作业区域),避免设计过度冗余或不能达到相应指标。也可以辅助运动精度校验,通过比较理论计算出来的末端执行器位置和实际给定关节变量输出的位置,分析末端位姿误差,优化关节/连杆结构或参数,改进控制算法,提升机器人末端执行器的定位精度。
2 DH参数法
DH参数法是进行机器人正运动学分析的经典方法,其采用一种广义的矩阵代数的系统描述机器人相对于固定参考系的空间几何,这种方法采用4x4齐次变换矩阵来描述两个相互连接的刚性构件的空间关系,将正运动学问题简化为寻求等价的4x4齐次变换矩阵,将执行器的坐标系与参考坐标系进行关联。
使用DH参数法进行机器人正运动学分析主要有如下几个步骤:
1.对机器人系统简化。为了便于后续正运动学分析,对要分析的机器人系统或其中的驱动机构进行结构等效或简化(可以采用抓大放小的思路),使其能用一系列的"连杆"构成的系统来描述。其中,两连杆之间连接且可运动的部分称之为"关节"。
2.确定DH参数。每个连杆可用四个运动学参数来描述,即a,α,d,θ。
a(连杆长度):一个连杆两端之间的距离,即连杆两端关节轴公垂线的长度。
α(连杆转角):一个连杆的两端关节轴轴线间的夹角。
d(偏距):两个相邻连杆(杆两端关节轴公垂线)在公共轴线方向上的距离。
θ(关节角):两个相邻连杆(杆两端关节轴公垂线)绕公共轴线旋转的夹角。
其中a和α两个参数用于描述连杆本身,是连杆本身固有的属性。另外两个参数d和θ用于描述连杆之间的连接关系(关节属性),可以作为关节变量。当为旋转关节时,关节角θ为变量;当为位移关节时,偏距d为变量。
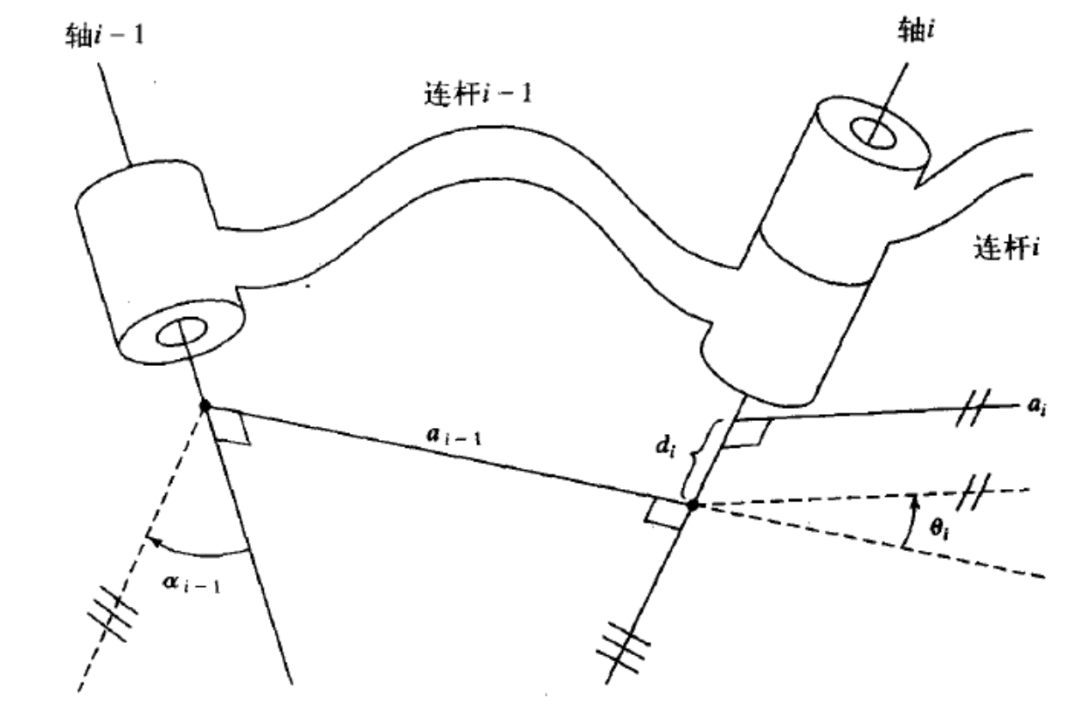
3.构建连杆坐标系。在正运动学分析中,坐标系需要构建在各个关节上。可以通过某种方式来确定坐标系的x,y,z轴的方向。如图是采用Craig DH法(改进DH法)建立连杆坐标系。
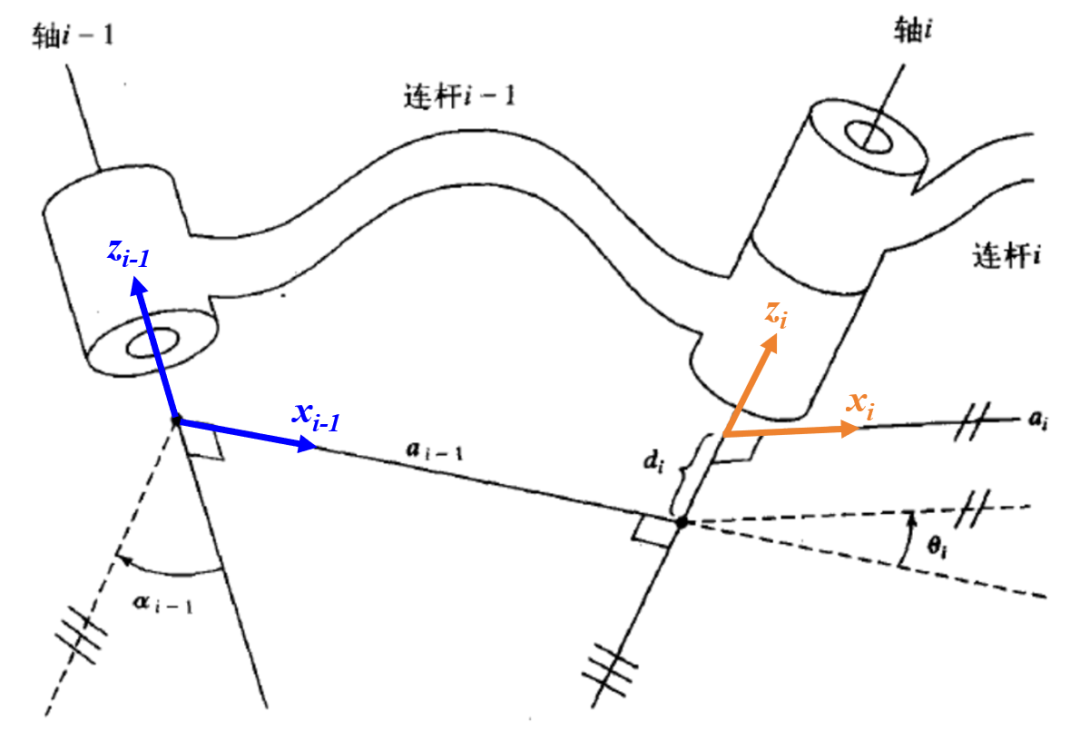
这种方法的特点是每一个连杆坐标系的z轴和原点固连在该连杆与前一个连杆连接处(关节)的轴线上(连杆首端轴线上)。比如对于坐标系{i},其z轴就在连杆i和连杆i-1关节处的轴线上(这里默认向上,具体方向根据实际情况为准)。对于其原点,不仅在这条轴线上,更是这条轴线和关节轴i与关节轴i+1的公垂线的交点。其x轴,位于关节轴i与关节轴i+1的公垂线上,方向由i指向i+1,继而可以通过右手定则确定y轴。对坐标系{i-1},坐标系{i+1}等的建立同理。
4.坐标变换。正运动学分析的目的是为了确定末端执行器的姿态,因此还需要通过坐标变换将末端关节的坐标系映射到基坐标系,以反映末端执行器相对于基座处于什么样的一个状态。而这一映射过程就需要进行坐标变换。
根据坐标变换中的内容,若想将坐标系{i-1}变换到坐标系{i},既需要进行旋转变换,还需要位移变换。
对于示例中的连杆结构较为复杂,不能相对直观地通过几何分析的方式直接推算出齐次变换矩阵。因此,可以采用"拆分"的方式,将整个变换过程拆解成若干个基本的旋转变换以及位移变换,最后组合成一个完整的变换。具体拆解方式如图所示。
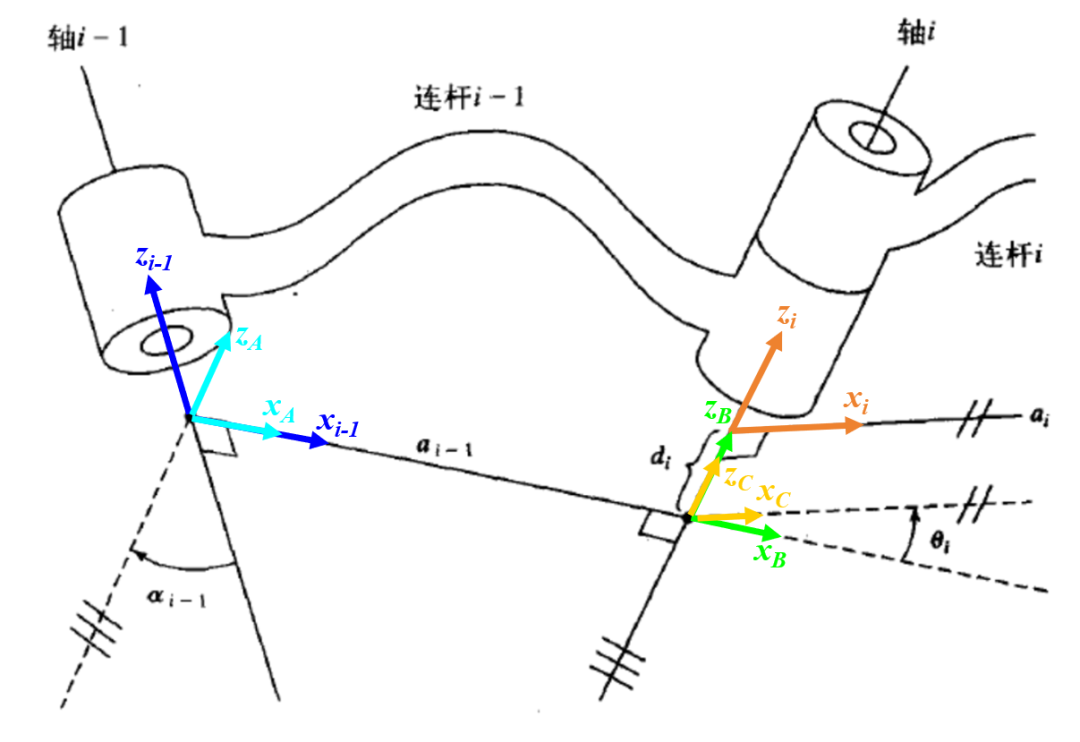
具体的变换步骤是:
(1) 将坐标系{i-1}绕xi-1 轴旋转αi-1 角,使坐标系{i-1}变换到坐标系{A},此时zA 与zi方向一致。
(2) 将坐标系{A}沿着xA 轴移动ai-1 距离,使坐标系{A}变换到坐标系{B},此时zB 与zi 方向一致,并与关节轴线i重合。
(3) 将坐标系{B}绕zB 轴旋转θi 角,使坐标系{B}变换到坐标系{C},此时xC 与xi方向一致。
(4) 将坐标系{C}沿着zC 轴移动di距离,使坐标系{C}变换到坐标系{i},此时已完成从坐标系{i-1}到坐标系{i}的变换。
因此,从坐标系{i-1}变换到坐标系{i}的齐次变换矩阵就可以通过各个基本的旋转变换和位移变换组合出来:
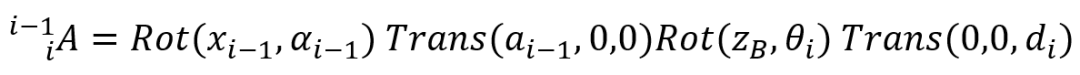
由矩阵乘法可得一般表达式:
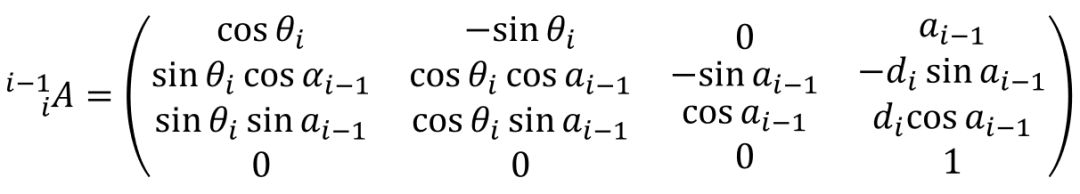
由此,得出连杆坐标系两相邻连杆的坐标变换的齐次变换矩阵。这样就可以通过这个齐次变换矩阵根据相应的关节变量,进行正运动学分析,进而对末端执行器的位姿进行分析。
3 案例分析
如果对一个2自由度的机械臂进行正运动学分析,首先需要将其转换成用连杆表示的系统。
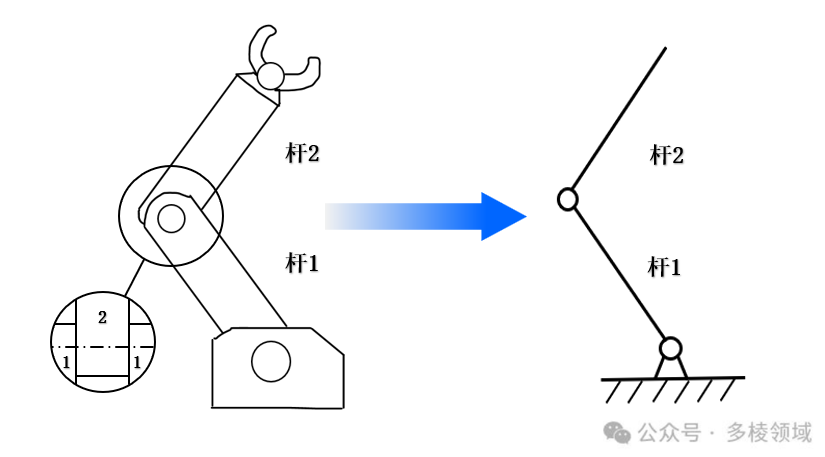
接着,确定DH参数。对于连杆长度a,杆1和杆2分别是连杆长度为l1 和l2。由于两个连杆为直杆,两端并没有形成角度,所以两个杆的连杆转角α为0;两个杆为旋转关节,所以关节角θ为变量,而且两个连杆之间没有偏置,故两连杆偏置为0。
继续建立坐标系,若根据"逐步拆解"的思想,将整个变换过程分解成若干个基本变换。如下图所示,设机械臂的基座坐标系为坐标系{0},对于杆1两端的坐标系分别设置为{1}和{2}(对应连接基座端和连接杆2端,即连杆1的首末端),杆2两端的坐标系分别设置为{3}和{4}(对应连接杆1端和末端执行器,即连杆2的首末端)。其中,坐标系z轴方向默认朝向屏幕外。
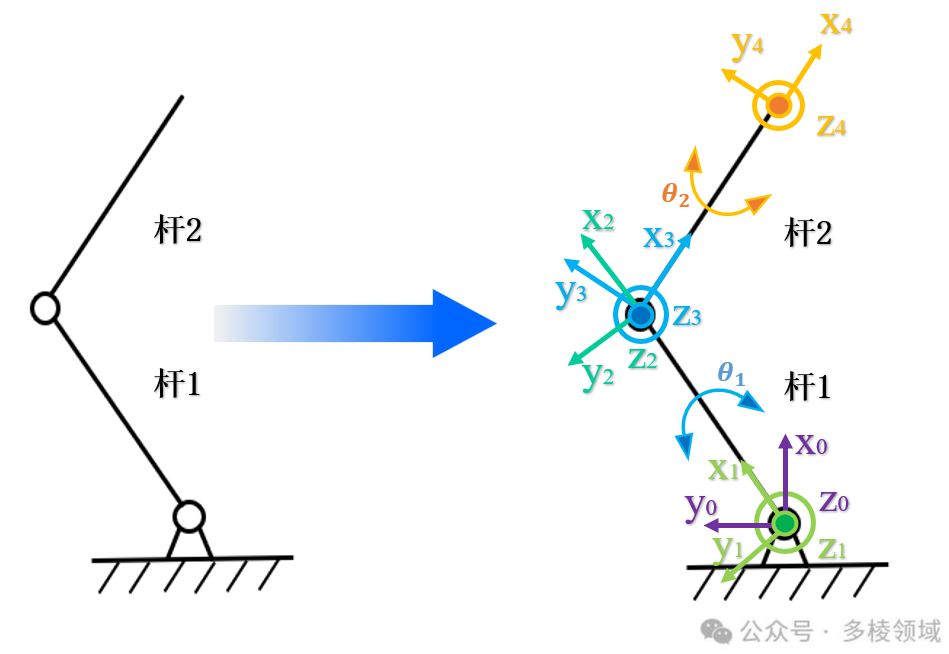
具体需要经过的基本变换过程依次为:坐标系{0}绕着z0旋转θ1角变换到坐标系{1},坐标系{1}沿着x1移动为l1 距离变换到坐标系{2},坐标系{2}绕着z2旋转θ2角变换到坐标系{3},坐标系{3}沿着x3移动l2距离变换到坐标系{4}。那么最终可以列出由坐标系{0}变换到坐标系{4}的齐次变换矩阵。
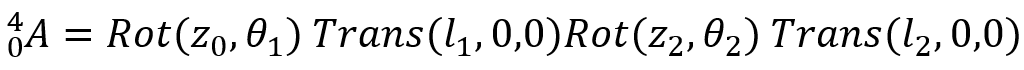
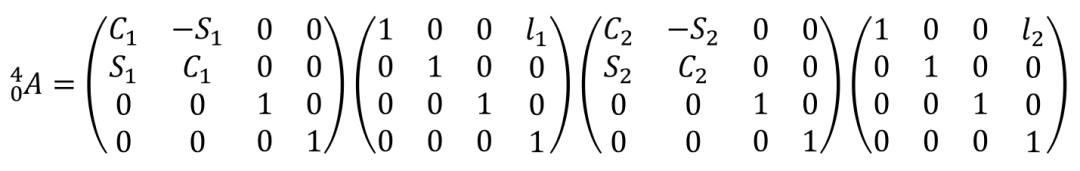
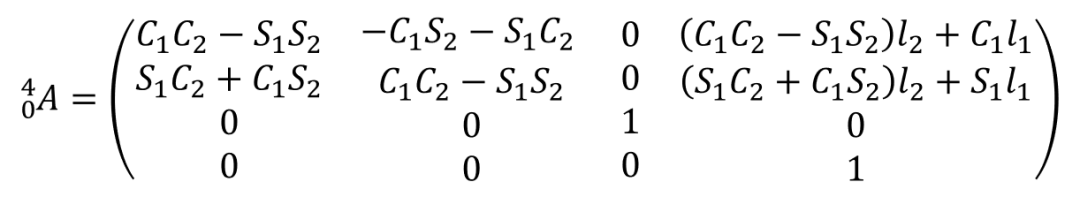
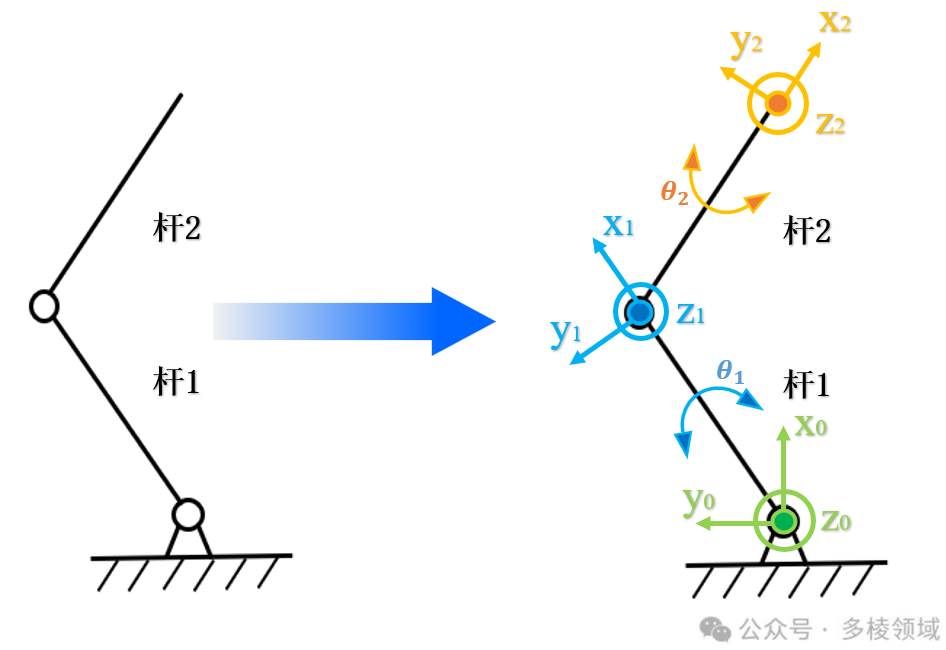
如果采用Craig DH法(改进DH法)建立连杆坐标系。建立坐标系如下图所示。设置基座坐标系为{0},杆1坐标系为{1},杆2坐标系为{2},末端执行器坐标系为{3}。
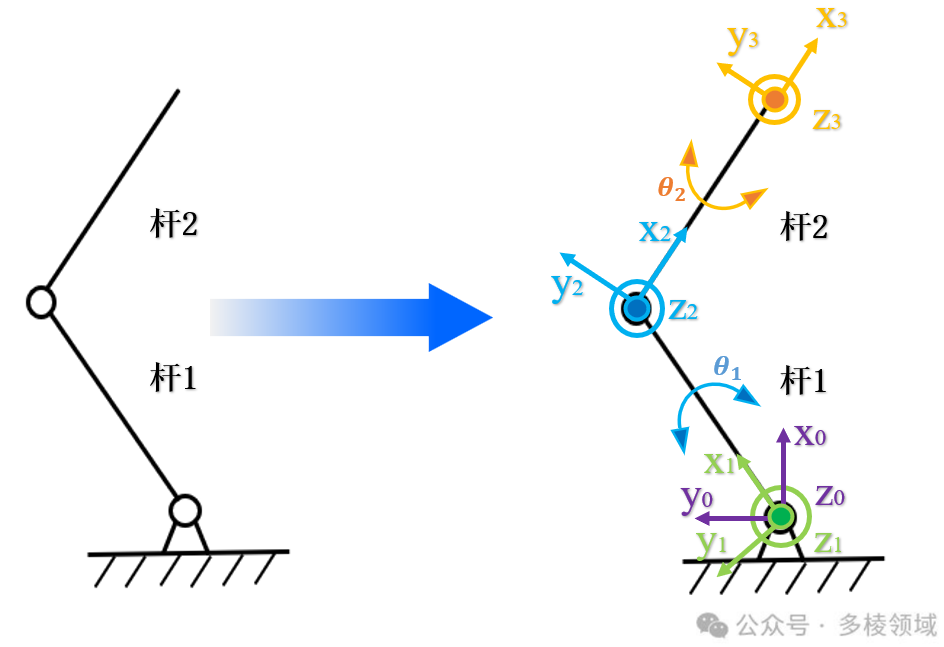
由此,变换流程为基座坐标系{0}→杆1坐标系{1}→杆2坐标系{2}→末端执行器坐标系{3}。那么最终可以列出由坐标系{0}变换到坐标系{3}的齐次变换矩阵。
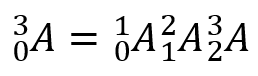
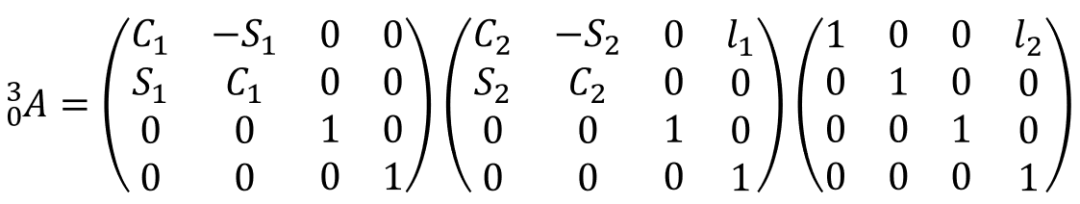
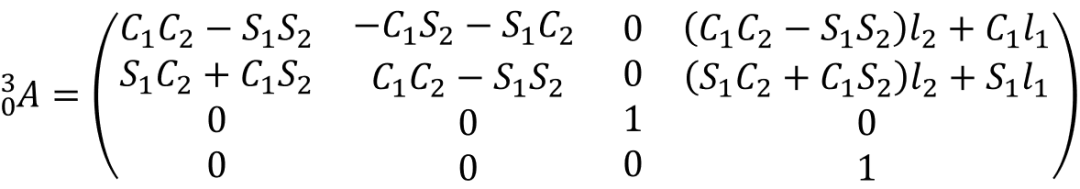
进一步的,如果把坐标系原点设置在连杆的末端,即采用Standard DH法(标准DH法),如下图所示。设置基座坐标系为{0},杆1末端坐标系为{1},杆2末端(末端执行器)坐标系为{2}。由于此时坐标系建立在连杆末端,所以可以直接描述连杆末端的位姿,因此坐标系x轴设置为与当前连杆共线。
由此,变换流程为基座坐标系{0}→杆1末端坐标系{1}→杆2末端坐标系(末端执行器)坐标系{2}。需要注意的是,从坐标系{0}变换到坐标系{1}中的位移变换是沿着杆1方向进行的,因此坐标系{1}的原点在坐标系{0}上来看坐标点是(l1 C1,l1 S1,0),故此位移变换向量为(l1 C1,l1S1,0)。坐标系{1}变换到坐标系{2}同理。那么最终可以得出由坐标系{0}变换到坐标系{2}的齐次变换矩阵。
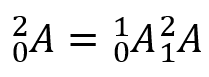
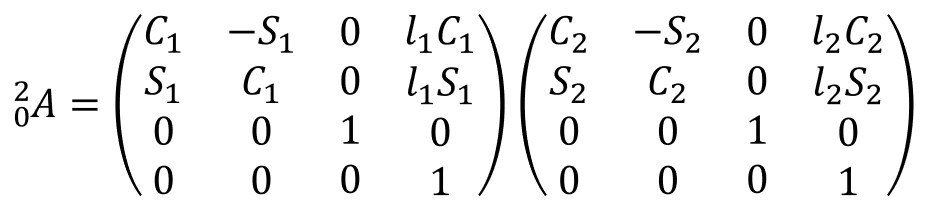
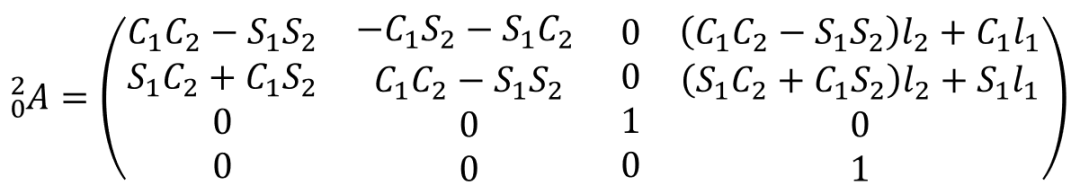
可以看到,上面三种建立坐标系的方法最终都能得到同样的齐次变换矩阵,其中Standard DH法和Craig DH法的建立坐标系区别也只是前者在杆件末端建系,后者在杆件首端建系。因此,进行正运动学分析的本质就是探寻末端执行器坐标系相对于基坐标系的齐次变换矩阵,而其中不同的建系方法及坐标变换只是探寻这个齐次变换矩阵的数学工具。
当然,上述只是采用DH法进行正运动学分析的步骤示例,有时会先进行坐标系建立后再确定DH参数,具体流程根据实际情况而定。
还有,本例中基坐标系默认z轴在关节轴线上且指向屏幕外,x轴向上。在建立坐标系时,需要结合实际应用情况,比如,根据厂家机器人手册中规定的坐标轴方向建立坐标系。
结语
本文介绍了机器人的正运动学分析,可以为**机器人结构设计、运动仿真及控制算法开发提供一定的支撑。**如果本文对您有所帮助,欢迎点赞,留言,转发,最后也欢迎您的关注,共同学习与进步!