有一个大小为 k 的滑动窗口,它从数组的最左边移动到最右边。
你只能在窗口中看到 k 个数字。
每次滑动窗口向右移动一个位置。
例如:该数组为
[1 3 -1 -3 5 3 6 7],k 为 3。则有:
窗口位置 最小值 最大值 [1 3 -1] -3 5 3 6 7 -1 3
你的任务是确定滑动窗口位于每个位置时,窗口中的最小值。
输入格式
输入包含两行。
第一行包含两个整数 n 和 k,分别代表数组长度和滑动窗口的长度。
第二行有 n 个整数,代表数组的具体数值。
同行数据之间用空格隔开。
例如输入:8 3
1 3 -1 -3 5 3 6 7
输出:
-1 -3 -3 -3 3 3 解题思路:
首先,对于这种滑动窗口的题目,我们通常是使用队列来处理,因为窗口滑动中,在窗口进出的元素完美符合 队列FIFO(先进先出)的特性,在此基础上,如果我们要求滑动窗口中的最大/最小值,可以进一步使用 单调队列(在每一次的窗口内,其中的元素都保持单调有序)
单调队列,顾名思义,就是队列中的元素全部都保持同一种单调性,例如单调递增,那么我们为什么要在这题中实现单调队列呢?
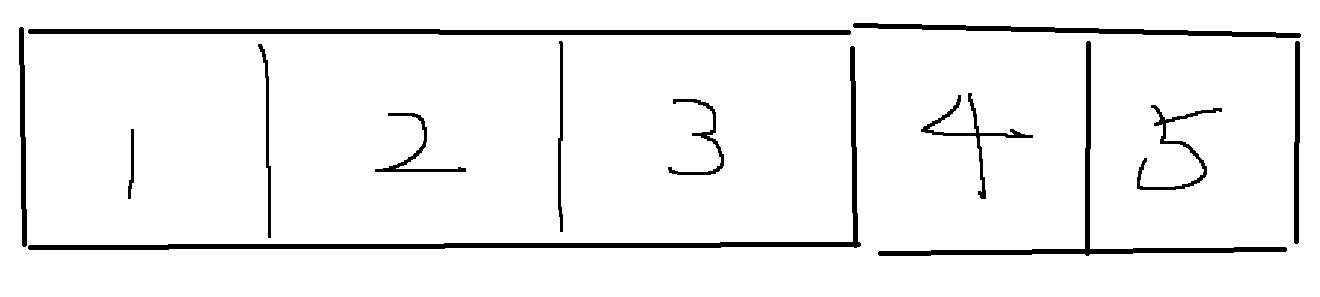
题目要求我们求出每次滑动窗口中最小的值,首先对于这样一个数组 ,我们的滑动窗口不断向右滑动,在每次移动的过程中,我们的队尾元素(3是队尾,4是即将入队的元素序列):
加入此时滑动窗口 的队尾 元素序列是3,那么下一次要增加的队尾元素序列就是4,如果在3这个位置元素 = 10, 而 4这个位置元素 = 5 ,显然3号位 > 4号位 ,如果我们将 4号入队,那么根据题意求窗口中的最小值(假如k=3),在4号位加入窗口中后,3号位随着窗口的右移,是永远不会成为窗口中的最小值的(因为3号位元素 > 4号位元素),而且3号位元素 出队的时间也要快于4号位,也就是说:
只要4号位进入窗口的那一刻,这个三号位在滑动窗口中就毫无意义了,根本就用不到他。
这种当前队尾元素 > 即将入队的元素的情况,我们可以直接将无用元素删去:
cpp
while(队尾元素>当前索引元素){
tt--; //队尾指针--
}
q[++ tt] = i; //重新赋值队尾元素为对应的当前索引i> 这里的q[tt]存储的是原数组的下标位置
按这种模式,每一次的窗口滑动,当前最小值的下标,永远都只会是 滑动窗口队列中的队头元素,因为我们入队的最小值一直在向前移动(tt--)
这样,当前每一次的滑动窗口队列就是单调递增,我们要取最小值,只需要取当前窗口队列中的队头元素就可以了,时间复杂度仅为O(1)
接下来我们再来处理细节问题:
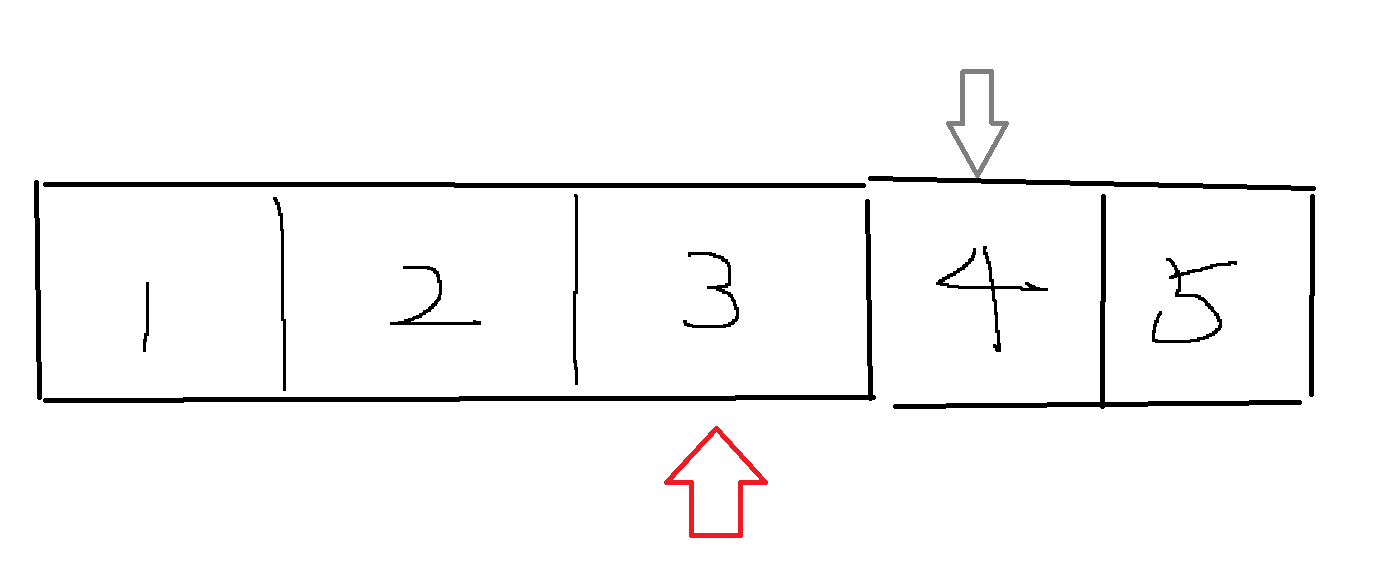
1、窗口的移动:队头应该及时更新位置:
如果队头hh < 队尾tt (这里指的是队列的性质 ) 同时 当前队头在原数组中的序列位置 < 当前索引i -k+1(也就是窗口长度),这表示窗口已经走过了上次的队头了,所以队头hh++,将下一个元素作为窗口新队头。
cpp
//当前索引为i
if(hh<=tt && q[hh] < i-k+1) hh++; 这里的hh++,对应的是我们放到队列中的队头的下一个元素,例如现在队列中如果对应的是【1,2,3】
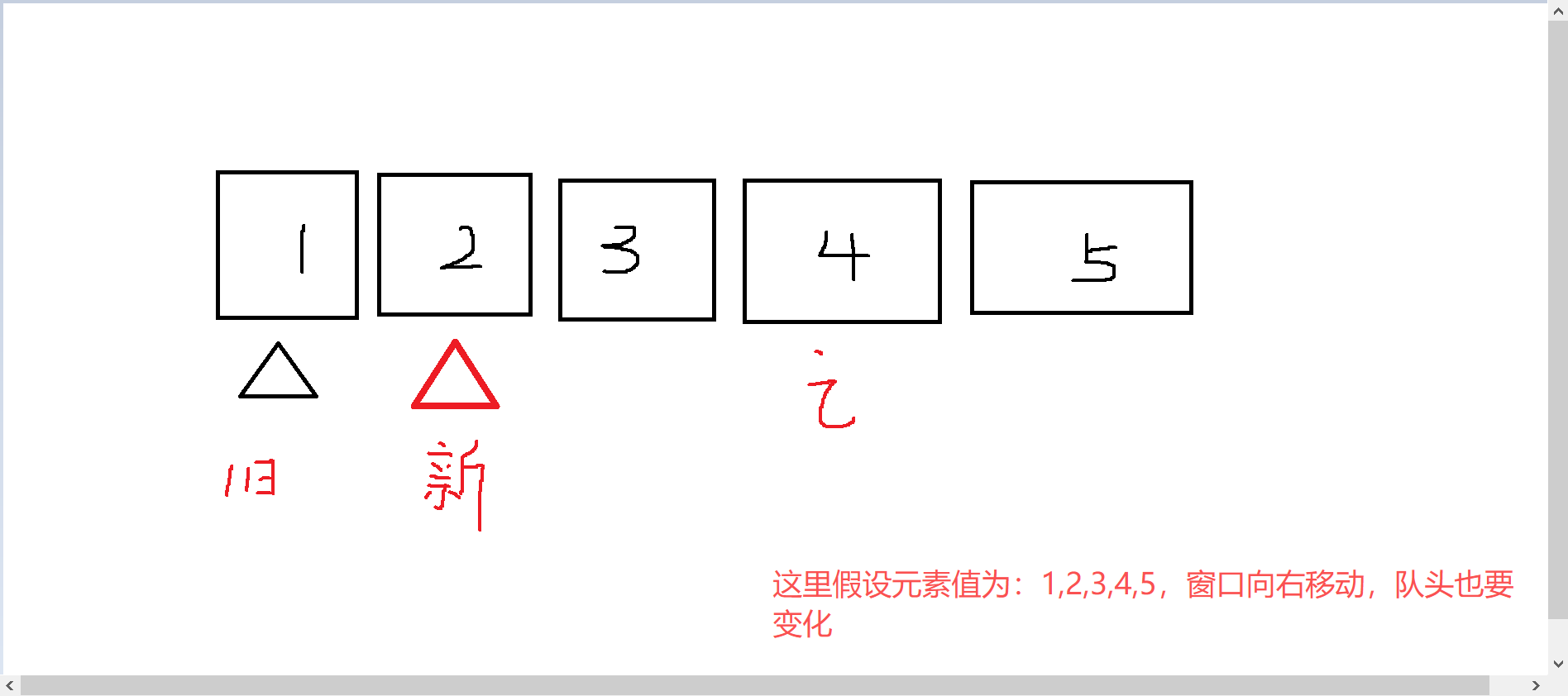
注意,这个【1,2,3】不是滑动窗口包含的值,不是[1 3 -1] -3 5 3 6 7这样的,而是我们自己创建的队列,这个队列元素里包含的信息,就是原数组的元素下标。
在这个队列中,1表示队头,3表示队尾,q[0] = 1,q[1] = 2,q[2] = 3,这表明这个数组 [1 3 -1] -3 5 3 6 7此时窗口内的最小值下标就是q【0】,这个元素值就是a【q【0】】
此时hh就是1的位置,tt就是3所在的位置,接下来4来了,当我们的当前窗口的左边界,走出了这个q【0】的位置,不论这个4对应的元素大小如何,我们都不能让【1,2,3】中的这个【1】继续进来比较了,所以hh++,移动到了2的位置,此时队头就是2,对应q【0】 = 2;现在队列对应的就是【2,3,4】(这是每次入队元素都大于队头元素的情况,其他情况原理一样)
此时新队头在原数组中的序列就是q[hh++]
cpp
#include <iostream>
using namespace std;
const int N = 1e6+10;
int a[N],q[N]; //a[N]原数组;q[N]单调队列,存储元素索引
//注: q[N] 存储的是数组 a 的元素索引(而非值)
int main()
{
int n,k; //n是数组长度,k是窗口大小
scanf("%d%d",&n,&k);
for(int i =0;i<n;i++)
scanf("%d",&a[i]);
//以上是输入操作
//求最小值
int hh = 0; //队头
int tt = -1; //队尾
for(int i =0;i<n;i++)
{
if(hh<=tt && q[hh] < i-k+1) hh++; //如果队头不在当前滑动窗口里面,就出队删除这个队头
while(hh<=tt && a[q[tt]] >= a[i]) tt--; //删掉单调队列中的这个队尾元素
q[++ tt] = i; //重新赋值队尾元素为对应的当前索引i
//单调递增的,所以最小值一定是在队头的位置
//i > k-1 是为了保证滑动窗口完整出现
if(i >= k - 1) printf("%d ", a[q[hh]]);
}
return 0;
}举个实际的例子吧:
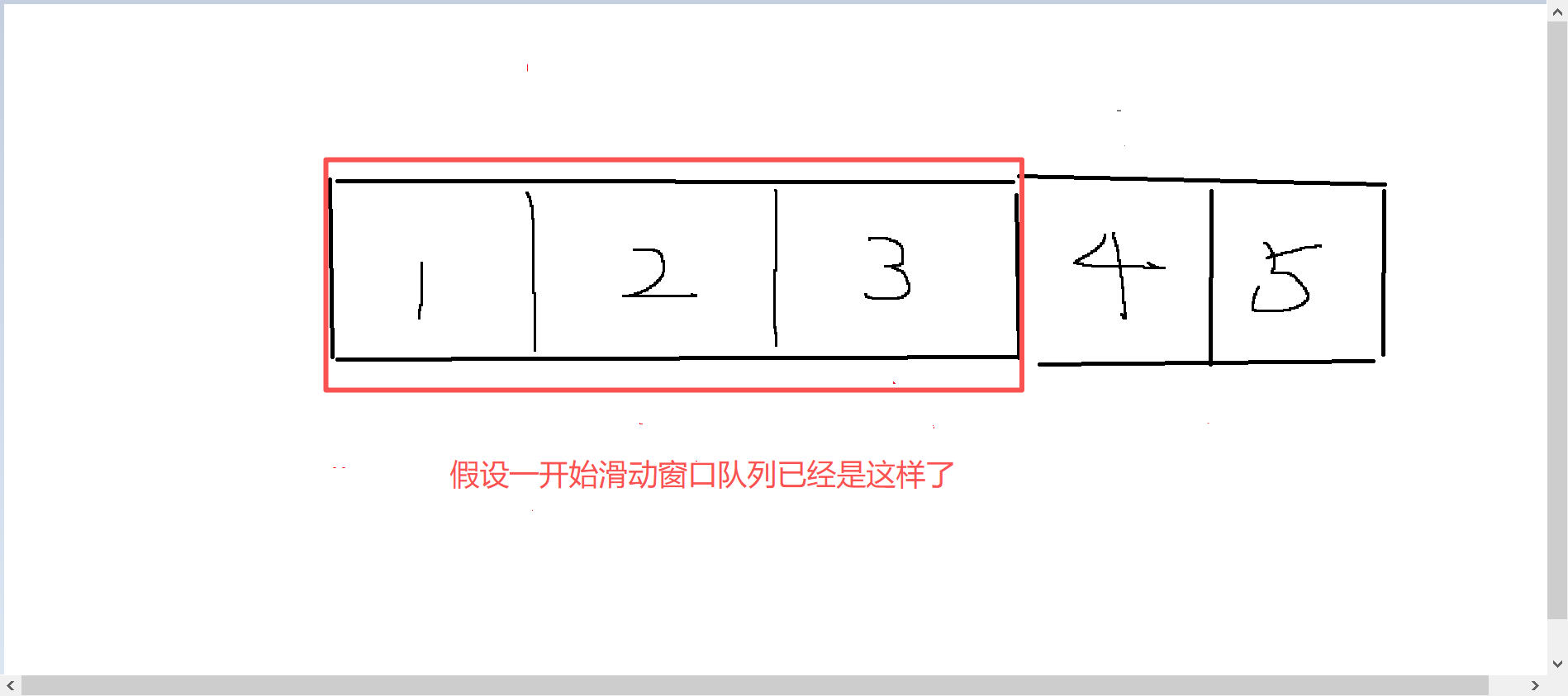 要注意,我们的q[tt]中记录的是序列i的值,这是通过一开始q[++tt] = i 得出来的
要注意,我们的q[tt]中记录的是序列i的值,这是通过一开始q[++tt] = i 得出来的
首先窗口右移,我们的hh队头自然也要往右移动hh++,这个时候q[hh]自然就 == 1,但此时tt依旧还在原来的位置
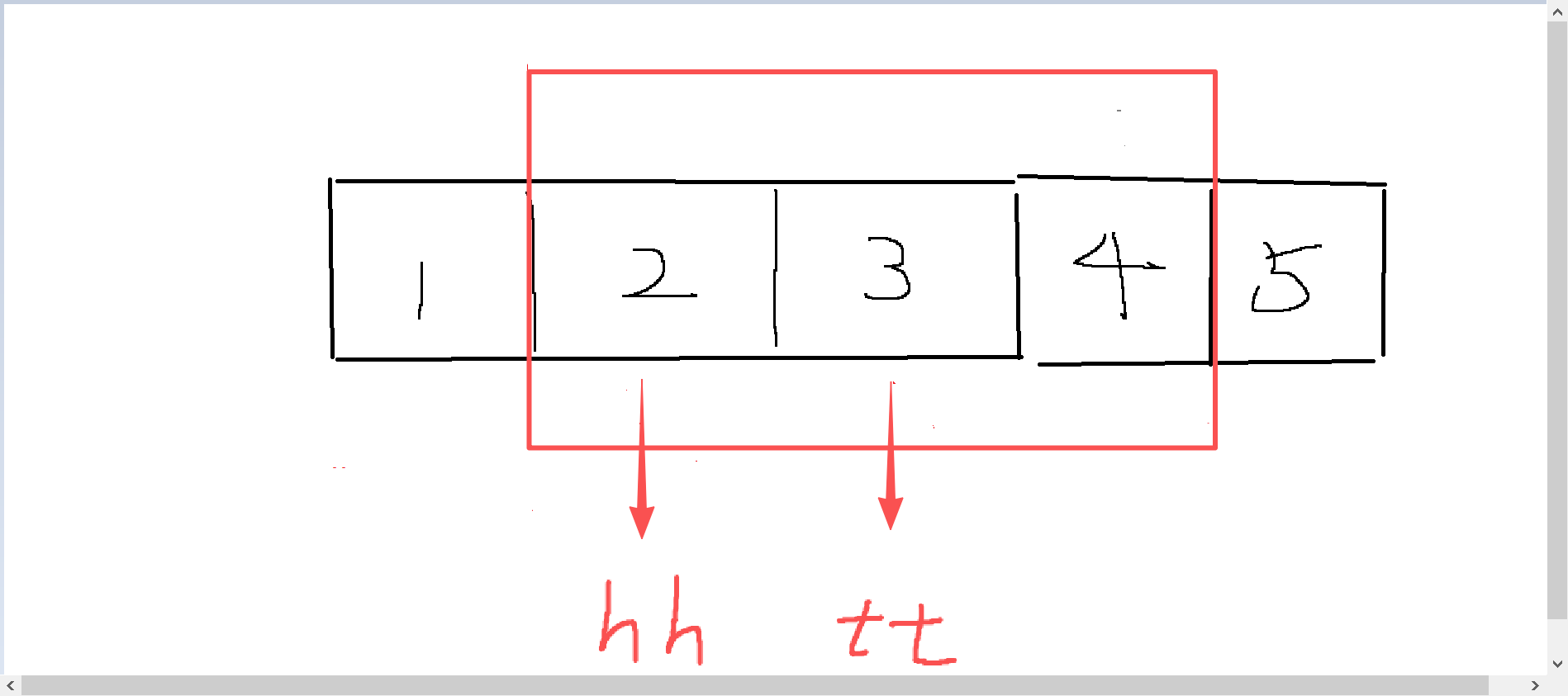
用tt对应在原数组的元素与新入队的元素比大小,假如新入队元素很小,那么tt--,一直tt--到不满足while条件,那就执行q[++tt] = i;
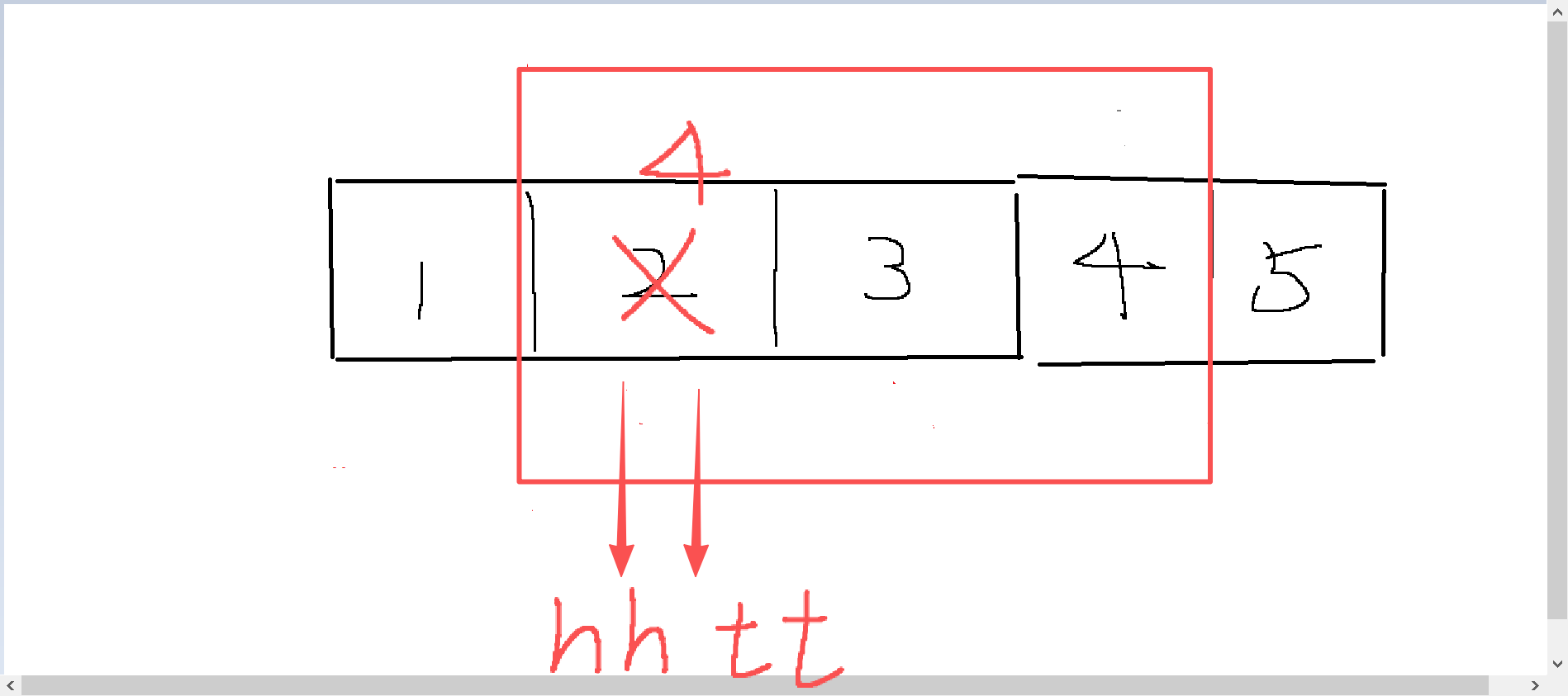
其实这个时候窗口队列中只剩下:

此时这个窗口队列中的hh == tt , 而q[hh] = q[tt] =3(数组从0序列开始) , 此时窗口队列中只有一个元素 【3】,如果此时要输出最小值,那么就是直接打印a[q[hh]],也就是a[3]
接下来 i 继续往下走,对于 if(hh<=tt && q[hh] < i-k+1) hh++; 我们可以看到,现在的q[hh] ==3,不会满足这个q[hh] < i-k+1的条件
如果比较完后依旧最小,那么就取代原来的tt:
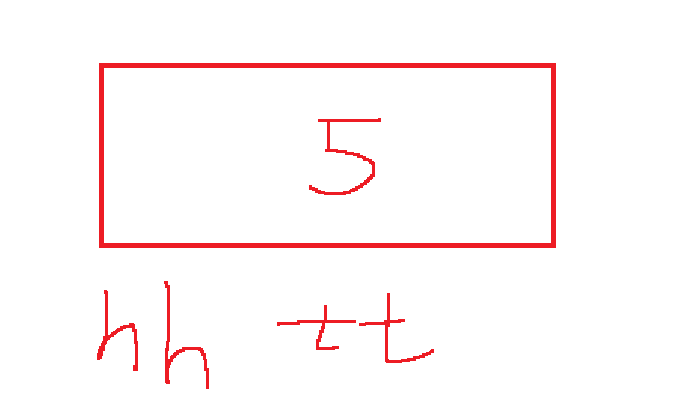
此时q[hh] =q[tt] =4,整个窗口队列中只有一个元素[5]
同时如果新元素比较后不是最小的,那么就让新元素的序列入队:q[++tt] = i
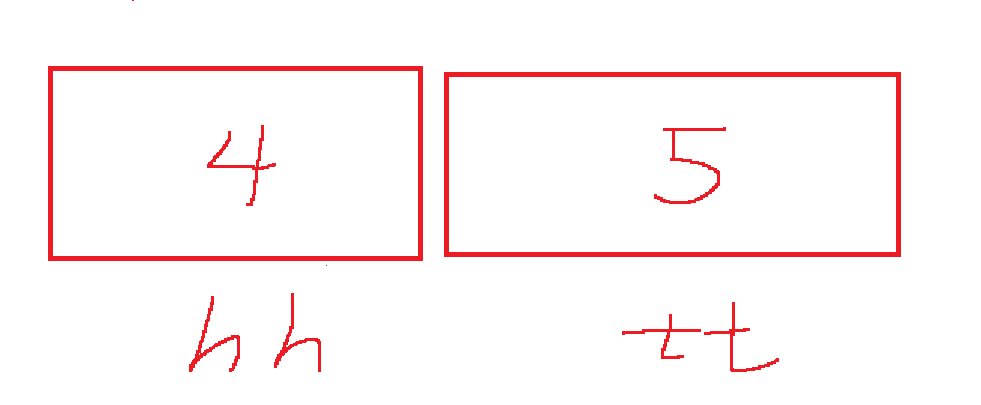
这个时候输出对应的最小值,就是输出a【q【hh】】,也就是a【3】
如果下一个元素再来,这个4 依旧还是最小的,那么最小值依旧输出a【q【hh】】,也就是a【3】
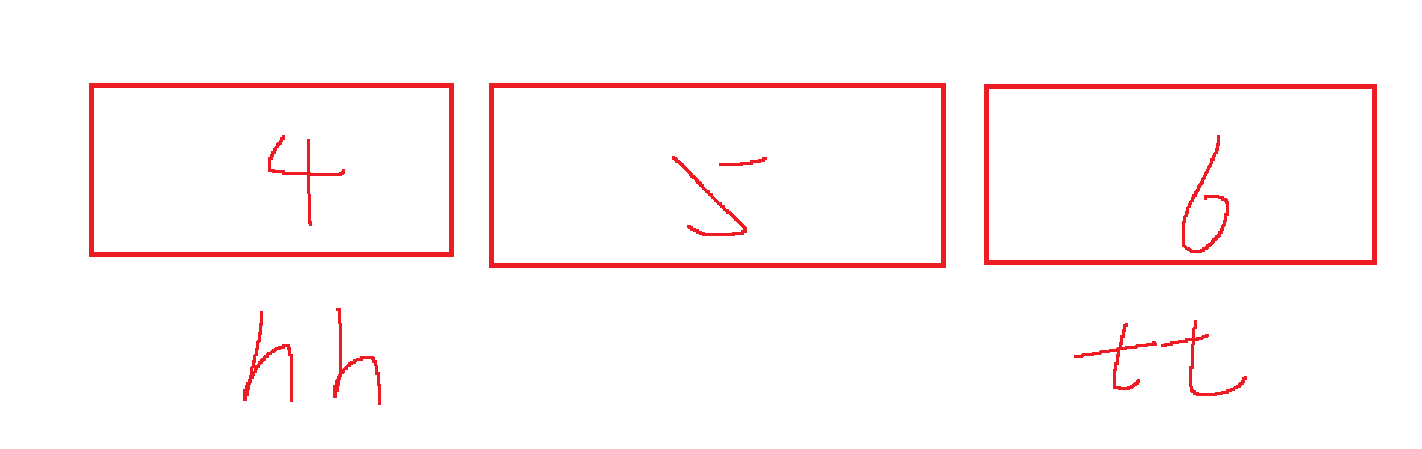
可以看到,如果这个4一直最小,在他进入这个窗口的那一刻起,他最多可以输出3次最小值,直到他被踢出窗口,也就是if(hh<=tt && q[hh] < i-k+1) hh++; //如果队头不在当前滑动窗口里面,就出队删除这个队头
(下图加入7对应的元素依旧大)这个时候这个5就是最小值
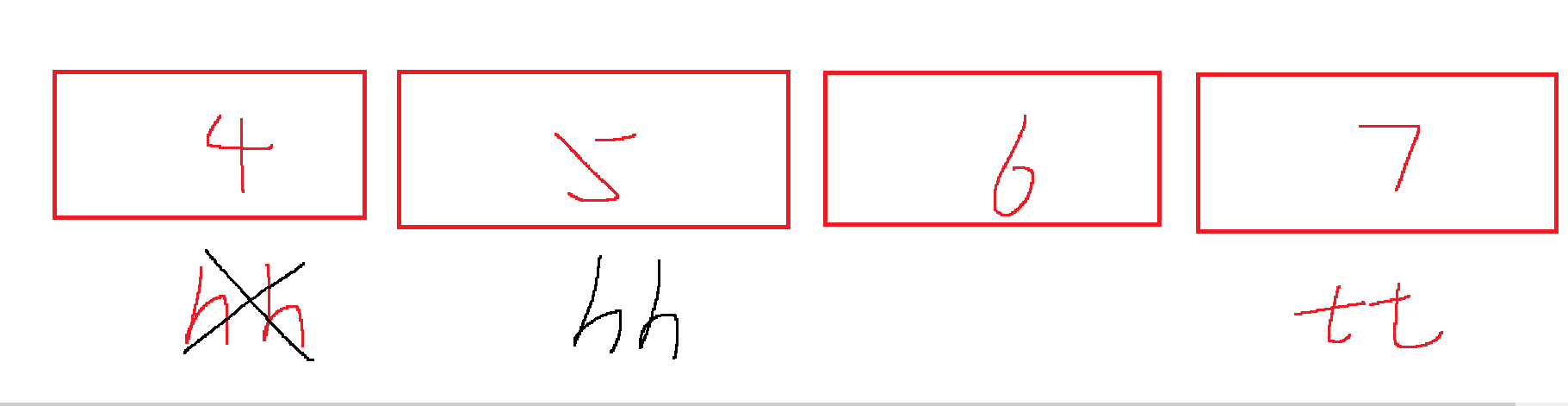
可以看出,我们这个窗口队列从【1,2,3】直接转变为了【4】,然后是【4,5】【4,5,6】【5,6,7】
在这个窗口中,我们始终保持这是一个单调递增的元素关系,每次只需要拿去队列中的队头序列,然后a【q【hh】】就是这个窗口中的最小值。