题目
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交:
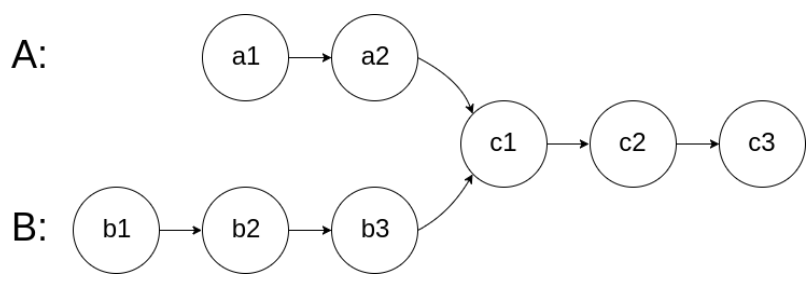
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
自定义评测:
评测系统 的输入如下(你设计的程序 不适用 此输入):
intersectVal - 相交的起始节点的值。如果不存在相交节点,这一值为 0
listA - 第一个链表
listB - 第二个链表
skipA - 在 listA 中(从头节点开始)跳到交叉节点的节点数
skipB - 在 listB 中(从头节点开始)跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构,并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点,那么你的解决方案将被 视作正确答案 。
数据范围
listA 中节点数目为 m
listB 中节点数目为 n
1 <= m, n <= 3 * 104
1 <= Node.val <= 105
0 <= skipA <= m
0 <= skipB <= n
如果 listA 和 listB 没有交点,intersectVal 为 0
如果 listA 和 listB 有交点,intersectVal == listA[skipA] == listB[skipB]
测试用例
示例1
java
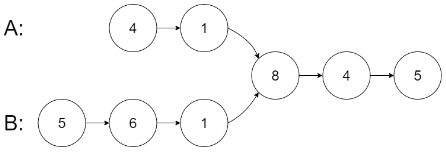
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at '8'
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
--- 请注意相交节点的值不为 1,因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说,它们在内存中指向两个不同的位置,而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点,B 中第四个节点) 在内存中指向相同的位置。示例2
java
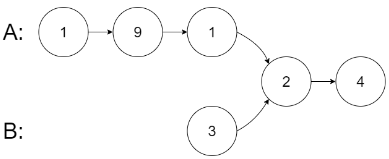
输入:intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Intersected at '2'
解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [1,9,1,2,4],链表 B 为 [3,2,4]。
在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。示例3
java
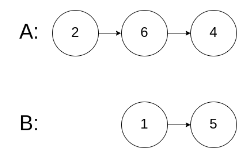
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:No intersection
解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。
由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
这两个链表不相交,因此返回 null 。题解(双指针)
java
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if(headA==null||headB==null){
return null;
}
ListNode a=headA,b=headB;
while(a!=b){
a= a==null?headB:a.next;
b= b==null?headA:b.next;
}
return a;
}
}思路
这道题用空间复杂度为n的解法很简单,一个哈希数组就行了,但我们追求的肯定不止这样。
另一种双指针的空间复杂度为1的解法就比较考验积累和数学功底了,大家背下来的就行了。
大致逻辑为,两个双指针从两条链表开头同时遍历,谁先到达表尾就将这个指针指向另一个链表的开头。这样操作,两个指针最终会汇聚到相交位置,或确定不相交,具体推到我就引用官解了,官解讲得很好。
下面提供双指针方法的正确性证明。考虑两种情况,第一种情况是两个链表相交,第二种情况是两个链表不相交。
情况一:两个链表相交
链表 headA 和 headB 的长度分别是 m 和 n。假设链表 headA 的不相交部分有 a 个节点,链表 headB
的不相交部分有 b 个节点,两个链表相交的部分有 c 个节点,则有 a+c=m,b+c=n。
如果 a=b,则两个指针会同时到达两个链表相交的节点,此时返回相交的节点;
如果 a =b,则指针 pA 会遍历完链表 headA,指针 pB 会遍历完链表 headB,两个指针不会同时到达链表的尾节点,然后指针 pA 移到链表 headB 的头节点,指针 pB 移到链表 headA 的头节点,然后两个指针继续移动,在指针 pA 移动了 a+c+b 次、指针
pB 移动了 b+c+a 次之后,两个指针会同时到达两个链表相交的节点,该节点也是两个指针第一次同时指向的节点,此时返回相交的节点。
情况二:两个链表不相交
链表 headA 和 headB 的长度分别是 m 和 n。考虑当 m=n 和 m =n 时,两个指针分别会如何移动:
如果 m=n,则两个指针会同时到达两个链表的尾节点,然后同时变成空值 null,此时返回 null;
如果 m =n,则由于两个链表没有公共节点,两个指针也不会同时到达两个链表的尾节点,因此两个指针都会遍历完两个链表,在指针 pA 移动了 m+n 次、指针 pB 移动了 n+m 次之后,两个指针会同时变成空值 null,此时返回 null。