
💡Yupureki:个人主页
🌸Yupureki🌸的简介:

目录
[1. 在排序数组中查找元素的第一个和最后一个位置](#1. 在排序数组中查找元素的第一个和最后一个位置)
[2. 牛可乐和魔法封印](#2. 牛可乐和魔法封印)
[3. 烦恼的高考志愿](#3. 烦恼的高考志愿)
[1. 木材加工](#1. 木材加工)
[2. EKO / 砍树](#2. EKO / 砍树)
[3. 跳石头](#3. 跳石头)
前言
当我们的解ret具有二段性时,可以使用二分算法。其中ret是题目的最优解,例如较小值中的最大值,较大值中的最小值。
二分查找
1. 在排序数组中查找元素的第一个和最后一个位置
题目链接:

算法原理
题目的关键是非递减顺序
那么在[1,2,4,4,5,6,7,8]我们单独看4,我们会发现4之前的数字全部小于或等于4,之后的数字全部大于或等于4大。那么如何找出第一次出现的4?
我们可以发现,如果看5这个数字,那么5之后的不用看了,因为一定大于4,只用看之前的数字
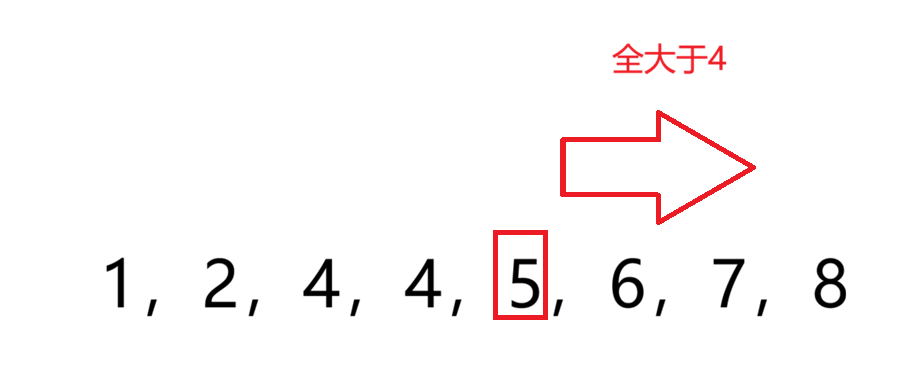
如果看2这个数字,那么2之前的也不用看了,因为一定小于4,只用看2后面的数字。

因此我们单独看一个某数字,作比较就能忽略之前或之后的某一个区间,因为数组是非递减的,具有单调性。这里我们选择left和right,为数组的下标,初始left为0,right为数组的最大下标
表示在[left,right]区间(注意是闭区间)中找数字target,通过之前的分析,我们选择mid为[left,mid]这个区间的中间,即mid = (left + mid)/2 或者(left + right + 1)/2,(我们后面讲如何选择),target = 4
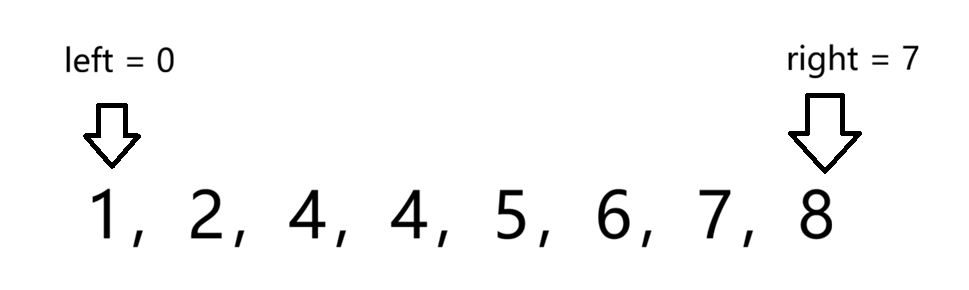
如果v[mid]>=4,那么mid后面的区间不用看了,肯定全部大于4,所以我们只需要看[left,mid],即令right = mid;如果v[mid] < 4,那么mid前面的区间不用看了,肯定全部小于4,所以我们只需要看[mid + 1,right],即令left = mid + 1。

直到left = right,此时找到的是第一个4
那么代码可以这样写
cpp
int l = 1, r = n;
while(l < r)
{
int mid = (l + r) / 2;
if(v[mid] >= 4) r = mid;
else l = mid + 1;
}当然二分的模板肯定不只这一个

选择哪个模板取决于问题是什么,我们的check如何设计的。例如上个问题是找到第一个4

那么我们让check为v[mid] >= 4,这样我们就会找到一个区间,这个区间全都是大于或等于4的数字,而区间的左端点正好就是第一个4
那么为什么是r = mid 而不是r = mid -1? 因为我们判断的check是大于或等于4,因此如果mid正好落到了第一个4那里,我们让r = mid - 1,就会跳过第一个4
那如果check判断条件不包含=的情况,即v[mid] > 4,那么是不是r = mid - 1?很可惜,这样是错误的,这里不做推导。只需要记住check一定得包含=的情况即可
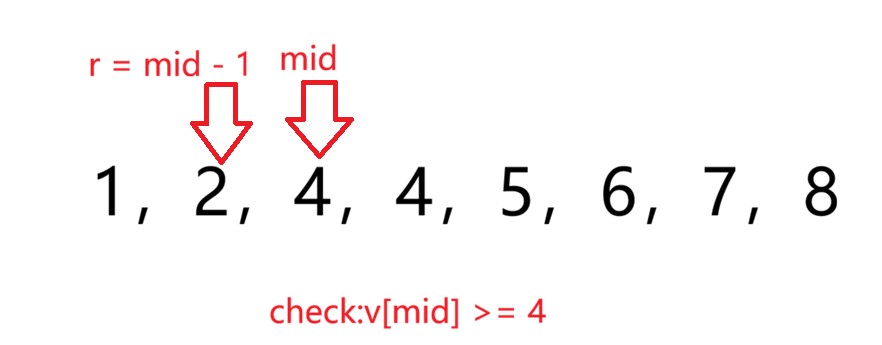
相反l = mid + 1就是对的而不是l = mid,因为会死循环,这里不做推导,记住即可
这是查找区间左端点的模板,那么何时使用查找区间右端点的模板?
例如我们要找最后一个出现的4的位置
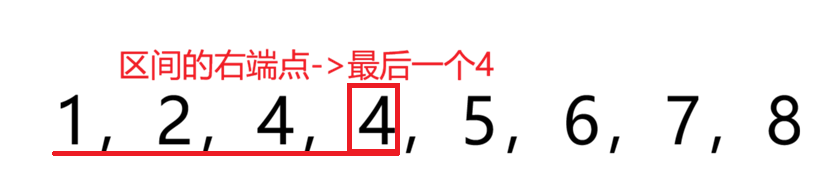
我们同样可以找到一个区间,这个区间全都是小于或等于4的数字,那么区间的右端点就是最后一个4
这里我们的check选择的是v[mid]<=4,而上面的模板是v[mid]>=4,为什么不一样?
因为我们要在小于或等于4的区间内找他的右端点,那肯定是v[mid]<=4
这里mid = (l + r + 1)/2,为什么不是(l + r)/2?因为会死循环,记住即可
然后就跟上面同理l = mid,r = mid - 1
实操代码
cpp
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
if(nums.size() == 0)
return {-1,-1};
int l = 0,r = nums.size() - 1;
while(l < r)
{
int mid = (l + r)/2;
if(nums[mid] >= target)
r = mid;
else
l = mid + 1;
}
if(nums[l] != target)
{
return {-1,-1};
}
int ret = l;
l = 0;r = nums.size() - 1;
while(l < r)
{
int mid = (l + r + 1)/2;
if(nums[mid] <= target)
l = mid;
else
r = mid - 1;
}
return {ret,l};
}
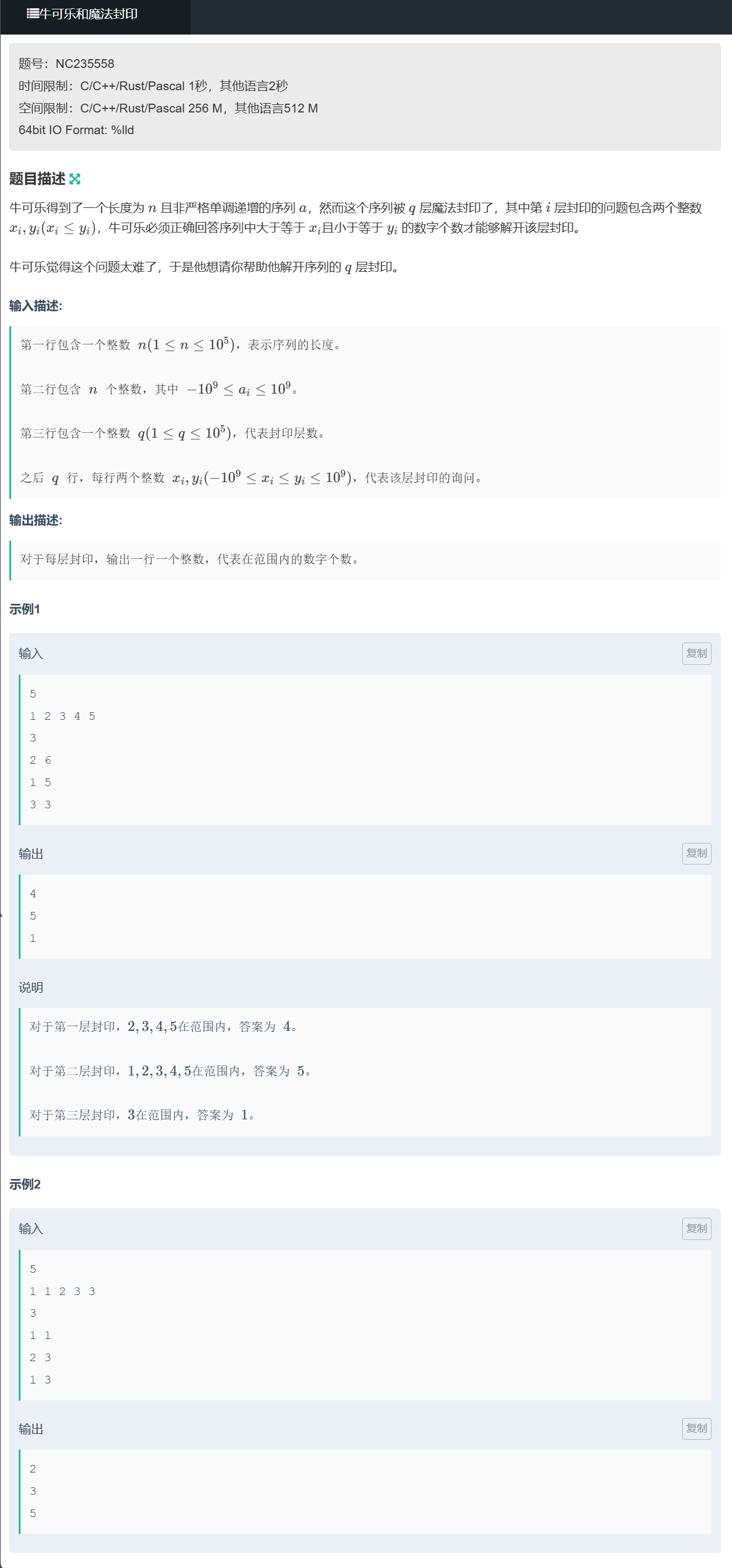
};2. 牛可乐和魔法封印
题目链接:
算法原理
由于是找到大于等于x且小于等于y的数字个数
我们可以看作在数组中找到第一个出现的x的位置,和最后一个出现的y的位置
这里我们引入两个接口,lower_bound和upper_bound

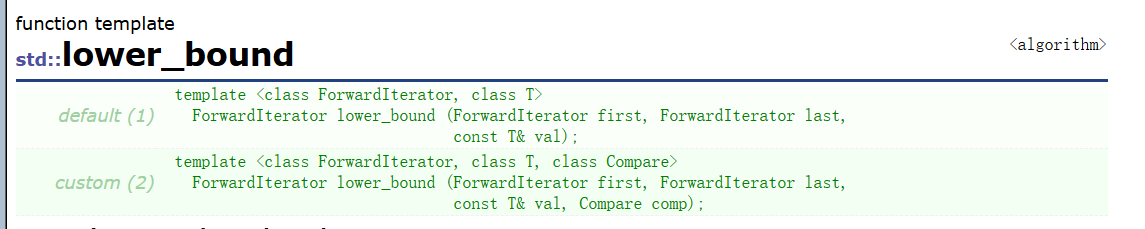
lower_bound表示在一个有序的容器内找到第一个大于或等于val的元素
upper_bound则表示找到第一个大于val的元素
因此我们可以利用lower_bound找到第一个大于或等于x的元素
利用upper_bound找到第一个大于val的元素
由于两个函数返回的都是迭代器,相减就能得到区间的长度
实操代码
cpp
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
int n;cin>>n;
vector<int> v;
while(n--)
{
int num;cin>>num;
v.push_back(num);
}
int m;cin>>m;
while(m--)
{
int left,right;cin>>left>>right;
cout<< upper_bound(v.begin(),v.end(),right) - lower_bound(v.begin(),v.end(),left) <<endl;
}
return 0;
}3. 烦恼的高考志愿
题目链接:

算法原理
本题其实就是在一个数组中找离n最近的一个数字
我们用lower_bound帮我们找大于或等于n的第一个数字m
- 如果n == m,那么毋庸置疑,离n最近的数字肯定就是n本身
- 如果m > n,那么要看n左右的数字,例如有2 3 5三个数字,5是大于或等于3的第一个数字,但实际上2离3才是最近的
实操代码
cpp
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
int n, m; cin >> n >> m;
vector<int> v;
while (n--)
{
int num; cin >> num;
v.push_back(num);
}
long long ret = 0;
sort(v.begin(), v.end());
while (m--)
{
int num; cin >> num;
auto it = lower_bound(v.begin(), v.end(), num);
if (it == v.end())
{
it--;
ret += num - *it;
}
else if (it != v.begin())
{
int n1 = *it - num;
it -= 1;
int n2 = num - *it;
ret += n1 > n2 ? n2 : n1;
}
else
ret += *it - num;
}
cout << ret;
return 0;
}二分答案
1. 木材加工
题目链接:

算法原理
我们要找到符合条件的最大长度
什么时候符合条件?能够切割l长度的段数一定要大于或等于k
那么我假设最大长度为lmax,那么我切1cm肯定符合条件,切2cm也符合条件,切lmax/2也符合条件,lmax也符合条件,直到lmax + 1就不够k段了。并且超过了lmax,不论多大,就是lmax * 1000也一定不符合条件
因此我们发现,如果把长度l作为一个数组,那么小于或等于lmax一定符合条件,大于lmax一定不符合
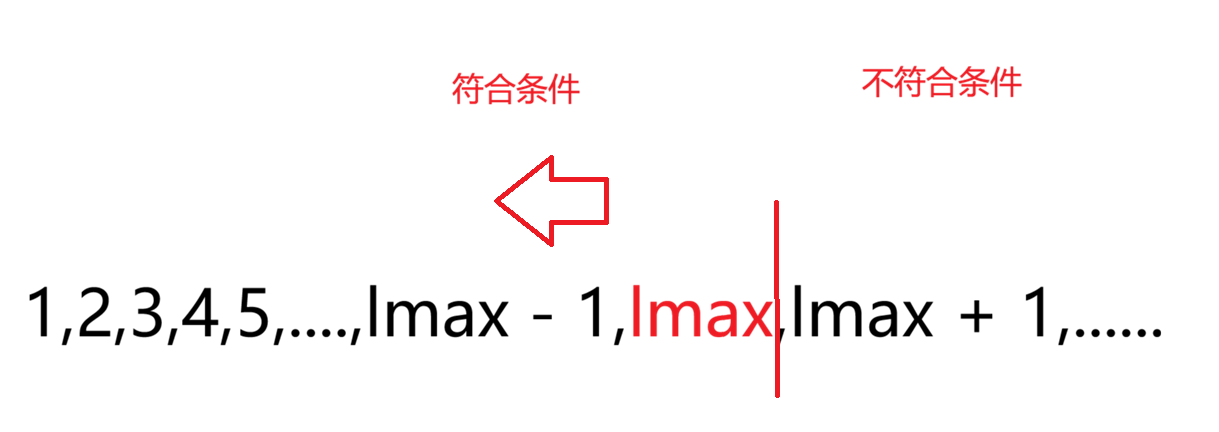
这其实就是个二分,我们找到[1,lmax]的右端点即可,此时一定是能够切割的最大长度
只是我们在答案中二分而已
实操代码
cpp
#include <iostream>
#include <vector>
using namespace std;
vector<int> v;
long long check(int k)
{
long long sum = 0;
for (auto& it : v)
{
sum += it / k;
}
return sum;
}
int main()
{
long long n, k; cin >> n >> k;
int max = 0;
for (int i = 0; i < n; i++)
{
int num; cin >> num;
v.push_back(num);
if (num > max)
max = num;
}
if (check(1) < k) {
cout << 0;
return 0;
}
int left = 1, right = max;
while (left < right)
{
int mid = (left + right + 1) / 2;
if (check(mid) >= k)
left = mid;
else
right = mid - 1;
}
cout << left;
return 0;
}2. EKO / 砍树
题目链接:

算法原理
这也是答案中的二分
假设我们无脑砍树,从高度为0开始砍,那肯定能够。如果从1开始,也够。直到h就不够了,并且h往上也肯定不够
实操代码
cpp
#include <iostream>
#include <vector>
using namespace std;
vector<int> v;
long long func(int n)
{
long long sum = 0;
for(auto & it : v)
{
int num = it - n;
if(num > 0)
sum += num;
}
return sum;
}
int main()
{
int n,k;cin>>n>>k;
int max = 0;
for(int i = 0;i<n;i++)
{
int num;cin>>num;
v.push_back(num);
if(num > max)
max = num;
}
int left = 0,right = max;
while(left < right)
{
int mid = (left + right + 1)/2;
if(func(mid) >= k)
left = mid;
else
right = mid-1;
}
cout<<left;
return 0;
}3. 跳石头
题目链接:
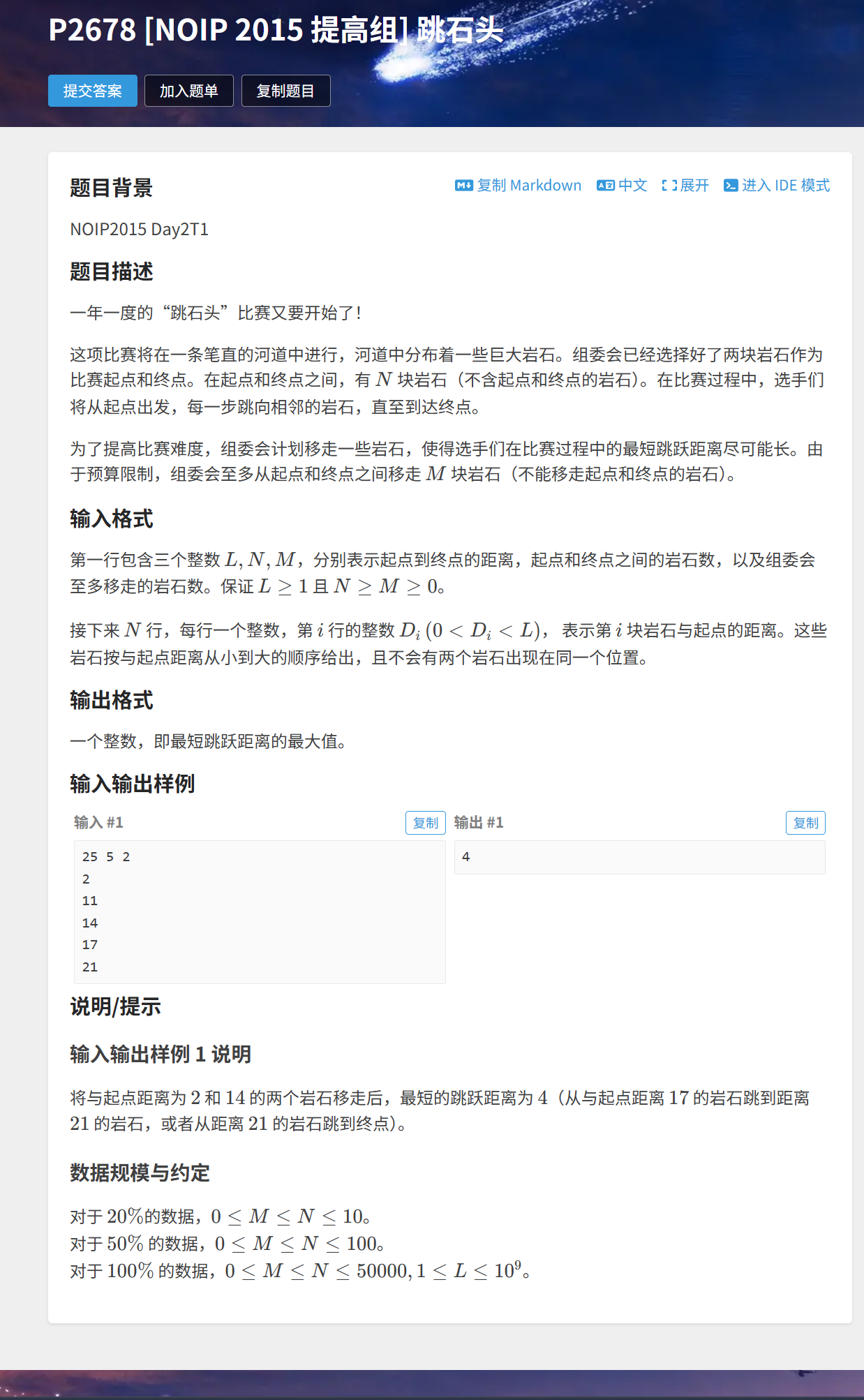
算法原理
我们先不找最大的最短跳远距离,我们先看哪些最短跳远距离符合条件
即移动的石头小于最大的移动次数
假设最短跳远距离很短,那就不会移动石头;如果很大,那么可能要移动很多石头,甚至全移走了都不够。因此最短跳远距离只会在左区间内产生,即保证移动的石头数小于最大次数。然后右端点就是最大的最短跳远距离
实操代码
cpp
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector<long long> v;
int L, N, M;
bool check(int d)
{
int count = 0;
int pos = 0;//上一个石头
for (int i = 1; i < v.size() - 1; i++)
{
if (v[i] - v[pos] < d)//距离小于最短跳远距离,则移动i号石头
count++;
else
pos = i;//大于最短跳远距离,则更新上一个跳远的石头
}
if (v.back() - v[pos] < d)
count++;
return count <= M;//判断移走石头的数量是否符合条件
}
int main()
{
cin >> L >> N >> M;
v.push_back(0);
for (int i = 0; i < N; i++) {
int num;
cin >> num;
v.push_back(num);
}
v.push_back(L);
sort(v.begin(), v.end());
int left = 1, right = L;
while (left < right)
{
int mid = left + (right - left + 1) / 2;//查找右端点
if (check(mid))
left = mid;
else
right = mid - 1;
}
cout << left;
return 0;
}