机器学习超参数调优全方法介绍指南

悟乙己2025-09-12 17:45

本篇文章Master Hyperparameter Tuning in Machine Learning适合希望深入了解超参数调优的读者。文章的亮点在于介绍了多种调优方法，如手动搜索、网格搜索、随机搜索、贝叶斯优化和元启发式算法，并通过实际案例展示了这些方法在复杂模型（如CNN）和简单模型（如SVM）中的应用效果。

文章目录

  • [1. 引言](#1. 引言)
  • [2. 什么是超参数调优](#2. 什么是超参数调优)
  • [3. 手动搜索](#3. 手动搜索)
    • [3.1 模拟](#3.1 模拟)
      • [3.1.1 构建和评估模型](#3.1.1 构建和评估模型)
      • [3.1.2 准备数据集](#3.1.2 准备数据集)
      • [3.1.3 搜索超参数](#3.1.3 搜索超参数)
      • [3.1.4 结果](#3.1.4 结果)
  • [4. 网格搜索](#4. 网格搜索)
    • [4.1 搜索空间](#4.1 搜索空间)
    • [4.2 模拟](#4.2 模拟)
    • [4.3 结果](#4.3 结果)
  • [5. 随机搜索](#5. 随机搜索)
    • [5.1 搜索空间](#5.1 搜索空间)
    • [5.2 模拟](#5.2 模拟)
    • [5.3 结果](#5.3 结果)
  • [6. 贝叶斯优化](#6. 贝叶斯优化)
    • [6.1 选择代理模型](#6.1 选择代理模型)
    • [6.2 高斯过程的数学形式](#6.2 高斯过程的数学形式)
    • [6.3 在搜索空间中寻找下一个评估点](#6.3 在搜索空间中寻找下一个评估点)
    • [6.4 搜索空间](#6.4 搜索空间)
    • [6.5 模拟](#6.5 模拟)
    • [6.6 结果](#6.6 结果)
  • [7. 元启发式算法](#7. 元启发式算法)
    • [7.1 元启发式算法如何工作](#7.1 元启发式算法如何工作)
    • [7.2 元启发式算法的类型](#7.2 元启发式算法的类型)
    • [7.3 搜索空间](#7.3 搜索空间)
    • [7.4 模拟](#7.4 模拟)
      • [7.4.1 步骤 1. 初始化：创建种群](#7.4.1 步骤 1. 初始化：创建种群)
      • [7.4.2 步骤 2. 评估：计算适应度分数](#7.4.2 步骤 2. 评估：计算适应度分数)
      • [7.4.3 步骤 3: 迭代](#7.4.3 步骤 3: 迭代)
      • [7.4.4 步骤 4 & 5: 选择最佳参数](#7.4.4 步骤 4 & 5: 选择最佳参数)
    • [7.5 结果](#7.5 结果)
  • [8. 泛化能力和时间效率的最终评估](#8. 泛化能力和时间效率的最终评估)
    • [8.1 泛化能力](#8.1 泛化能力)
    • [8.2 时间效率](#8.2 时间效率)
  • [9. 针对表格数据上训练的简单模型](#9. 针对表格数据上训练的简单模型)
    • [9.1 表格数据](#9.1 表格数据)
    • [9.2 搜索空间](#9.2 搜索空间)
    • [9.3 评估模型](#9.3 评估模型)
    • [9.4 结果](#9.4 结果)
      • [9.4.1 手动搜索](#9.4.1 手动搜索)
      • [9.4.2 网格搜索](#9.4.2 网格搜索)
      • [9.4.3 随机搜索](#9.4.3 随机搜索)
      • [9.4.4 贝叶斯优化 (Scikit-Optimize)](#9.4.4 贝叶斯优化 (Scikit-Optimize))
      • [9.4.5 遗传算法](#9.4.5 遗传算法)
  • [10. 结论](#10. 结论)

1. 引言

超参数调优是影响传统机器学习和深度学习模型性能的关键步骤。

虽然存在许多技术，但选择最佳调优方法取决于以下因素：

  • 模型复杂性：更复杂的模型自然会导致更大的搜索空间。
  • 数据复杂性：数据集的特性会影响调优难度。
  • 对模型的熟悉程度：我们对模型行为的理解可以指导调优选择并定义搜索空间。

在本文中，我将演示在不同场景下，如何使用五种关键调优方法来调优模型，包括：

  • 手动搜索 (Manual Search)
  • 网格搜索 (Grid Search)
  • 随机搜索 (Random Search)
  • 贝叶斯优化 (Bayesian Optimization)
  • 元启发式算法 (Metaheuristic Algorithm)

这些方法将应用于处理高维图像数据的卷积神经网络 (CNN) 和处理简单表格数据的核支持向量机 (Kernel SVM)。

2. 什么是超参数调优

超参数调优 是一个技术过程，用于在模型训练之前 调整机器学习模型的配置设置，这些设置被称为超参数。

与训练期间学习到的模型参数 （例如，权重和偏差）不同，超参数不是从数据中估计出来的，并且大多数机器学习模型都依赖于许多超参数。

例如，在卷积神经网络 (CNN) 的情况下，输入层形状 、卷积层设置 （如滤波器数量、滤波器大小、步长、填充）、输出层大小 以及编译器设置（如优化器、损失函数和评估指标）都确实是超参数。

因此，调优这些超参数是提高模型性能同时实现计算效率的关键步骤。

存在各种方法来处理这个调优过程。主要的方法，按复杂性和智能程度排序，包括：

  1. 手动搜索 (Manual Search)
  2. 网格搜索 (Grid Search)
  3. 随机搜索 (Random Search)
  4. 贝叶斯优化 (Bayesian Optimization)
  5. 元启发式算法 (Metaheuristic Algorithm)

每种方法在计算成本、搜索效率以及找到真正最优 配置（全局最优）的可能性之间提供了不同的权衡。

那么，让我们看看如何利用每个方法来解决一个真实世界的案例。

真实世界案例：工厂主的挑战

让我们想象一个场景，一位工厂主正在对用于高精度装配的小齿轮进行检查。

手动目视检查既慢又容易出错。

因此，工厂主计划开发一个基于 AI 的检查系统，使用 CNN 执行回归任务，从高分辨率相机捕获的图像中估计连续的半径值。

目标

我们这个项目的最终目标是找到 CNN 的最佳超参数组合并最小化泛化误差。

我将使用平均绝对误差 (MAE) 作为评估指标，因为它可以评估像素的精确度。

实际上，可以根据项目的目标设置适当的指标。

现在，让我们看看每种方法是如何工作的。

3. 手动搜索

手动搜索是最基本的方法，人类手动尝试不同的超参数值，训练模型，并评估其性能。

它通常由直觉、领域专业知识和先验经验驱动。

最佳使用场景：

  • 初步探索：刚开始使用新模型或数据集，需要大致了解超参数的影响。
  • 小搜索空间：适用于超参数很少或取值范围很窄的模型。
  • 有限的计算资源：计算能力非常有限，只能负担少量试验。

局限性：

  • 极其耗时，高度主观。
  • 对于复杂模型很少能找到真正最优的解决方案。

3.1 模拟

由于这是我们的第一次尝试，我将设置数据集以及用于评估模型的函数。

3.1.1 构建和评估模型

build_cnn_model 函数通过接受 hparams（一个超参数集合字典）作为参数来构建各种模式的 CNN。所有模型默认都将 MAE 作为其评估指标。

然后，evaluate_model 函数使用验证数据集构建、训练和评估每个模型。此函数返回训练好的模型和关键的评估指标：

  • eval_count：在调优过程中训练和评估的不同超参数集的数量，
  • total_time：从搜索开始到结束的总时间（秒），以及
  • mae：搜索期间生成的最佳 MAE 分数。
python 复制代码 
import tensorflow as tf  
from tensorflow import keras  
from keras import models, layers, optimizers, metrics, losses, backend, callbacks

def build_cnn_model(hparams: dict, input_shape=X_train.shape[1:]):  
      
    inputs = layers.Input(shape=input_shape)

      
    x = layers.Conv2D(hparams['filters_0'], (3, 3), activation='relu')(inputs)  
    if hparams.get('batch_norm_0', False): x = layers.BatchNormalization()(x)  
    x = layers.MaxPooling2D((2, 2))(x)

          
    for i in range(1, hparams.get('num_conv_layers', 1)):  
        if f'filters_{i}' in hparams:  
            x = layers.Conv2D(hparams.get(f'filters_{i}', 16), (3, 3), activation='relu')(x)  
            if hparams.get(f'batch_norm_{i}', False): x = layers.BatchNormalization()(x)  
            x = layers.MaxPooling2D((2, 2))(x)  
    x = layers.Flatten()(x)  
    x = layers.Dense(hparams['dense_units'], activation='relu')(x)  
    if hparams['dropout'] > 0: x = layers.Dropout(hparams['dropout'])(x)

      
    outputs = layers.Dense(1)(x)

      
    model = models.Model(inputs=inputs, outputs=outputs)  
    model.compile(  
        optimizer=optimizers.Adam(learning_rate=hparams['learning_rate']),  
        loss=losses.MeanSquaredError(),  
        metrics=[metrics.MeanAbsoluteError(name='mae')]  
    )  
    return model

def evaluate_model(hparams: dict, eval_count: int = 0, total_time: float = 0.0) -> tuple:  
    eval_count += 1  
    start_time = time.time()

          
    model = build_cnn_model(hparams)

      
    early_stopping = callbacks.EarlyStopping(  
        monitor='val_mae',  
        patience=5,  
        restore_best_weights=True,  
        verbose=1  
    )  
    model.fit(  
        X_train, y_train,  
        epochs=hparams.get('epochs', 100),  
        validation_data=(X_val, y_val),  
        batch_size=16,  
        callbacks=[early_stopping],  
        verbose=0  
    )

          
    _, mae = model.evaluate(X_val, y_val, verbose=0)

       end_time = time.time()  
    total_time += (end_time - start_time)

      
    backend.clear_session()

        return eval_count, total_time, mae, model

注意：由于其复杂性，CNN 很容易在训练数据集上过拟合。在回调中添加早停设置至关重要。

3.1.2 准备数据集

我从 1,000 张合成的 28 × 28 像素图像创建了训练、验证和测试数据集：

python 复制代码 
import numpy as np  
from sklearn.model_selection import train_test_split  
import numpy as np  
from sklearn.model_selection import train_test_split

img_height, img_width = 28, 28  
min_radius, max_radius = 1, 10  
n_samples = 1000  
images, targets = [], []

for i in range(n_samples):  
    img, target = generate_image_and_target(img_height, img_width, min_radius, max_radius, noise_level)  
    images.append(img)  
    targets.append(target)

X = np.array(images)  
X = X.reshape(n_samples, img_height, img_width, 1)  
y = np.array(targets)

X_tv, X_test, y_tv, y_test = train_test_split(X, y, test_size=200, random_state=42, shuffle=True)  
X_train, X_val, y_train, y_val = train_test_split(X_tv, y_tv, test_size=200, random_state=42, shuffle=True)

print(X_train.shape, y_train.shape, X_val.shape, y_val.shape, X_test.shape, y_test.shape)

(600, 28, 28, 1) (600,) (200, 28, 28, 1) (200,) (200, 28, 28, 1) (200,)

现在，让我们开始手动搜索。

3.1.3 搜索超参数

我随机定义了三种超参数组合，并选择了 MAE 最好的一个：

python 复制代码 
hparam_options = [  
    {  
        'num_conv_layers': 1,  
        'filters_0': 16,  
        'batch_norm_0': False,  
        'dense_units': 16,  
        'dropout': 0.0,  
        'learning_rate': 0.001,  
        'epochs': 50  
    },  
    {  
        'num_conv_layers': 1,  
        'filters_0': 16,  
        'batch_norm_0': False,  
        'dense_units': 16,  
        'dropout': 0.0,  
        'learning_rate': 0.001,  
        'epochs': 200  
    },  
    {  
        'num_conv_layers': 2,  
        'filters_0': 32,  
        'batch_norm_0': True,  
        'filters_1': 64,  
        'batch_norm_1': True,  
        'dense_units': 32,  
        'dropout': 0.1,  
        'learning_rate': 0.001,  
        'epochs': 100  
    },  
]

eval_count = 0  
total_time = 0.0  
best_mae = float('inf')  
best_hparams = None  
best_model = None

for item in hparam_options:  
    eval_count_returned, total_time_returned, current_mae, model = evaluate_model(hparams=item)  
    eval_count += eval_count_returned  
    total_time += total_time_returned

          
    if current_mae < best_mae:  
        best_mae = current_mae  
        best_hparams = item  
        best_model = model

return best_mae, eval_count, total_time, best_hparams, best_model

3.1.4 结果

  • 最佳 MAE：0.3663 像素（占总范围的 4.07%）
  • 执行时间：4.9146 秒
  • 评估总数：3
  • 最佳超参数集 ：
    num_conv_layers: 1, filters_0: 16, batch_norm_0: False, dense_units: 16, dropout: 0.0, learning_rate: 0.001, epochs: 200

hparam_options 中的第二个选项 被证明是最好的，MAE 为 0.3663 像素。

考虑到目标半径范围在 1 到 10 之间，预测误差约为总范围的 4.07% ([0.3663 / (10 - 1) \approx 0.04070])。

这将作为我的阈值。

4. 网格搜索

网格搜索系统地探索预定义、离散值集合（网格）内的所有可能的超参数组合。

例如，如果我们将学习率定义为在 [0.01, 0.001] 处测试，批量大小定义为在 [32, 64] 处测试，网格搜索将测试所有四种组合：[0.01/32, 0.01/64, 0.001/32, 0.001/64]。

最佳使用场景：

  • 明确定义的超参数空间：可以根据领域专业知识或先验经验，以合理的方式设置适度的超参数选项范围进行测试。
  • 需要穷尽搜索 ：需要绝对确定在搜索空间内找到最佳组合。
  • 可审计性：需要一个彻底且可复现的搜索过程，以用于合规性或理解。
  • 充足的计算资源：可以获得足够的计算能力来探索搜索空间中的每个组合。

局限性：

  • 当超参数数量及其选项增加时（例如，设置 5 个选项 x 10 个超参数 = 50 个模型需要训练和评估），计算成本会迅速变得昂贵。
  • 容易受到维度诅咒的影响。

4.1 搜索空间

网格搜索在其穷尽搜索的努力下，在较小的搜索空间中会更有效。使用过大的搜索空间可能导致耗时的过程。

因此，根据手动搜索中表现最佳的超参数，我定义了一个包含 36 种离散组合的小型搜索空间：

python 复制代码 
hparams_options = {  
    'num_conv_layers': [1],  
    'filters_0': [16, 32],  
    'batch_norm_0': [False],  
    'dense_units': [16, 32, 64],  
    'dropout': [0.0, 0.1, 0.2],  
    'learning_rate': [0.001, 0.0001],  
    'epochs': [200],  
}

4.2 模拟

我构建、训练并评估了 36 种 CNN 模式，并选择了 MAE 最好的一个：

python 复制代码 
from itertools import product

all_combinations_list = []  
eval_count = 0  
total_time = 0.0  
best_mae =  float('inf')  
best_hparams = None  
best_model = None

  
for num_conv in hparams_options['num_conv_layers']:  
    dynamic_filters_bn_combinations = list(  
        product(  
            *(hparams_options[f'filters_{i}'] for i in range(num_conv)),  
            *(hparams_options[f'batch_norm_{i}'] for i in range(num_conv))  
        )  
    )  
    base_combos = product(  
        hparams_options['learning_rate'],  
        hparams_options['epochs'],  
        hparams_options['dense_units'],  
        hparams_options['dropout']  
    )

        for base_combo in base_combos:  
        for dynamic_combo in dynamic_filters_bn_combinations:  
            hparam_set = {  
                'learning_rate': base_combo[0],  
                'epochs': base_combo[1],  
                'num_conv_layers': num_conv,  
                'dense_units': base_combo[2],  
                'dropout': base_combo[3]  
            }  
            filter_values = dynamic_combo[:num_conv]  
            for i in range(num_conv): hparam_set[f'filters_{i}'] = filter_values[i]  
            all_combinations_list.append(hparam_set)

  
for hparams in all_combinations_list:  
    eval_count_returned, total_time_returned, current_mae, model = evaluate_model(hparams=hparams)  
    eval_count += eval_count_returned  
    total_time += total_time_returned

      
    if current_mae < best_mae:  
        best_mae = current_mae  
        best_hparams = hparams  
        best_model = model

       return best_mae, eval_count, total_time, best_hparams, best_model

4.3 结果

  • 最佳 MAE：0.2675 像素（2.97% 误差范围）
  • 执行时间：124.7468 秒
  • 评估总数：36（测试了所有组合）
  • 最佳超参数集 ：
    num_conv_layers: 1, dense_units: 64, dropout: 0.0, filters_0: 16, learning_rate: 0.0001, epochs: 200

网格搜索实现了 2.97% 的误差范围 ，显著优于手动搜索（4.07%）。

执行耗时 125 秒（大约 2 分钟）。

除了狭窄的搜索空间 之外，早停在这里也发挥了关键作用，一旦误差下降变得微不足道，它就会停止不必要的训练周期，从而节省搜索时间。

由于其细致的方法，搜索结果显示了所定义搜索空间的全局最优解。

然而，扩大搜索空间和放宽正则化（早停设置）可能会找到不同的最优解，但会花费更多时间。

5. 随机搜索

随机搜索不是穷尽地检查每个组合，而是从指定的搜索空间中随机抽样固定数量的超参数组合。

搜索空间可以是连续的或离散的。这意味着超参数可以在给定范围内取任何实数值，而无需预定义的值（例如，学习率 = 0.012445 而不是 0.01）。

最佳使用场景：

  • 大型超参数空间：当超参数数量或其范围对于网格搜索来说过于庞大时。
  • 效率高于穷尽性：需要快速获得一个合理好的解决方案，特别是当只有少数超参数真正影响性能时。
  • 发现重要超参数：研究表明，在相同的计算预算下，随机搜索通常比网格搜索找到更好的结果，因为它更有可能探索广泛不同的值。

局限性：

  • 不能保证找到全局最优解，因为它依赖于随机抽样。
  • 解决方案的质量取决于迭代次数和抽样的随机性。

5.1 搜索空间

当它可以从大型搜索空间中尽可能随机地选择选项时，随机搜索表现最佳。

为了利用这一能力，我设置了一个极其庞大的搜索空间，包含广泛的值范围，以便它也可以生成随机连续值。

python 复制代码 
hparams_options = {  
      
    'num_conv_layers': [1, 2, 3, 4],  
    'filters_0': [16, 32, 48, 64],  
    'filters_1': [16, 32, 48, 64],  
    'filters_2': [16, 32, 48, 64],  
    'filters_3': [16, 32, 48, 64],  
    'batch_norm_0': [True, False],  
    'batch_norm_1': [True, False],  
    'batch_norm_2': [True, False],  
    'batch_norm_3': [True, False],  
    'dense_units': [32, 64, 96, 128],  
    'epochs': [i for i in range(100, 1001)]

      
    'dropout': [0.0, 0.5],  
    'learning_rate': [0.1, 0.0001]  
}

5.2 模拟

即使在相同的搜索空间内，随机搜索的结果在不同试验之间也会有所不同，因为它探索的是超参数的随机子集。

为了使结果标准化，我进行了五次试验 ，每次从搜索空间中随机选择了 50 种组合，并记录了最佳和平均结果。

在实践中，我们需要在进行大量试验以找到绝对全局最优解和限制耗时过程以获得一个合理好的次优解之间取得平衡。

python 复制代码 
eval_count = 0  
total_time = 0.0

best_mae = float('inf')  
best_hparams = None  
best_model = None

for _ in range(n_iterations):  
      
    hparams = dict()

      
    hparams['num_conv_layers'] = random.choice(hparams_options['num_conv_layers'])  
    for i in range(hparams['num_conv_layers']):  
        hparams[f'filters_{i}'] = random.choice(hparams_options[f'filters_{i}'])  
        hparams[f'batch_norm_{i}'] = random.choice(hparams_options[f'batch_norm_{i}'])  
    hparams['dense_units'] = random.choice(hparams_options['dense_units'])  
    hparams['epochs'] = random.choice(hparams_options['epochs'])

      
    hparams['learning_rate'] = random.uniform(hparams_options['learning_rate'][0], hparams_options['learning_rate'][-1])  
    hparams['dropout'] = random.uniform(hparams_options['dropout'][0], hparams_options['dropout'][-1])

      
    eval_count_returned, total_time_returned, current_mae, model = evaluate_model(hparams=hparams)  
    eval_count += eval_count_returned  
    total_time += total_time_returned

      
    if current_mae < best_mae:  
        best_mae = current_mae  
        best_hparams = hparams  
        best_model = model

return best_mae, eval_count, total_time, best_hparams, best_model

5.3 结果

在五次试验中，随机搜索平均实现了 2.48% 的误差范围，优于网格搜索的 2.97%。

搜索花费了 **216 秒（约 3.5 分钟）**来完成 50 次 CNN 模式测试；由于其庞大的搜索空间，速度略慢于网格搜索。

这个结果表明，随机搜索在速度和性能之间取得了良好的平衡，性能或时间上只有很小的折衷。

通过运行更多的试验和迭代，我们可以期待性能的进一步提升。

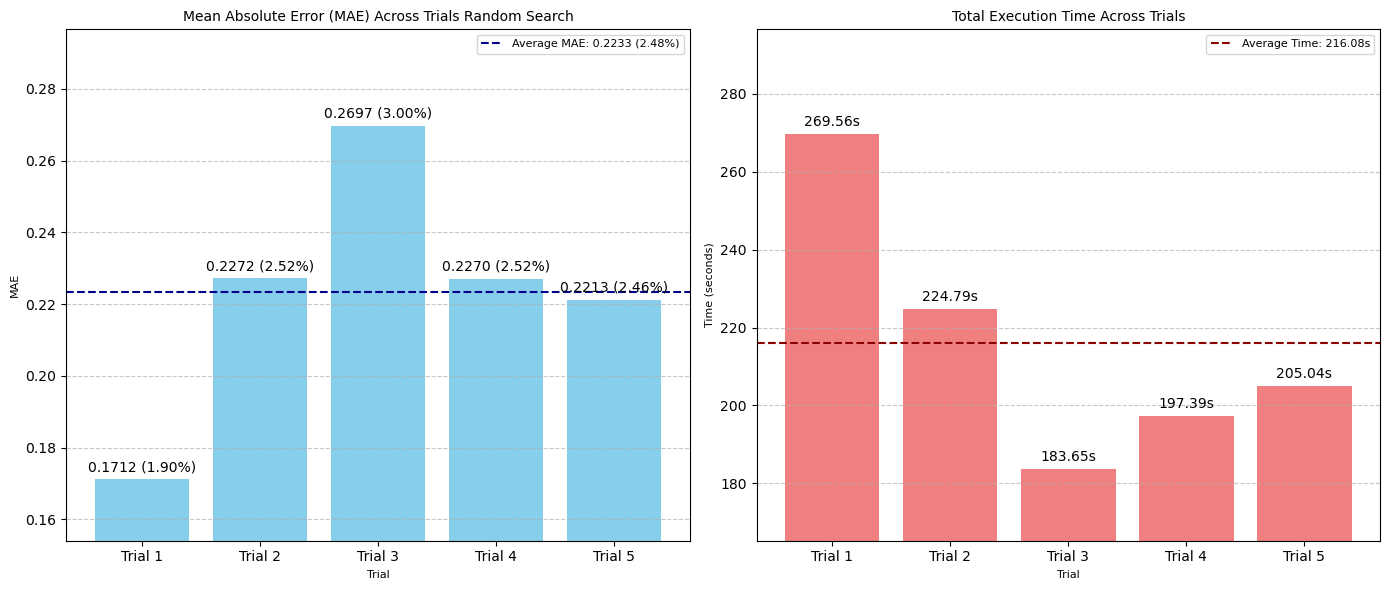
图：五次随机搜索试验中 MAE（左）和搜索时间（秒）（右）的比较

  • 最佳 MAE：0.1712 像素（1.90% 误差范围）
  • 平均 MAE：0.2233 像素（2.48% 误差范围）/ 试验
  • 平均执行时间：216.08 秒 / 试验
  • 评估总数：50 次 / 试验
  • 最佳超参数集 ：
    learning_rate: 0.010918659801547131, epochs: 200, num_conv_layers: 2, dense_units: 96, dropout: 0.0, filters_0: 32, batch_norm_0: True, filters_1: 32, batch_norm_1: False

注意：最优的 learning_rate 是 0.010918，证明了其评估连续值的能力。

6. 贝叶斯优化

与网格搜索或随机搜索不同，贝叶斯优化利用一种智能、样本高效的搜索方法，首先通过构建一个概率 的代理模型 （通常是高斯过程）。

高斯过程近似搜索空间中的目标函数，并估计每个 搜索点的高斯（正态）分布。

通过这个过程，贝叶斯优化可以查看具有置信区间的潜在搜索点的预期收益。

例如：

  • 搜索点（超参数组合）A ：预期收益 μ = 150 \mu = 150 μ=150，不确定性（风险） s i g m a 2 = 100 sigma^2 = 100 sigma2=100 → 高风险，高收益 → 探索
  • 搜索点（超参数组合）B ：预期收益 μ = 20 \mu = 20 μ=20，不确定性（风险）\\sigma\^2 = 20 → 低不确定性，低收益 → 有前景的点

为了决定下一步要评估哪个点，贝叶斯优化使用采集函数来量化这些预期值和不确定性，根据所选策略识别最有前景或最具探索性的点。

贝叶斯优化在给定迭代次数内持续这个搜索过程：

  1. 初始化：对目标函数进行少量初始随机评估。
  2. 训练代理模型 ：使用搜索空间中的样本训练代理模型。代理模型生成整个搜索空间上的均值 μ ( x ) \mu(x) μ(x)和方差 σ 2 ( x ) \sigma^2(x) σ2(x)。
  3. 计算采集函数：使用均值和方差计算搜索空间上的采集函数。
  4. 寻找下一个评估点 ：选择使采集函数最大化（或最小化）的点 x next x_{\text{next}} xnext。
  5. 评估目标函数 ：在 x next x_{\text{next}} xnext 处运行实际目标函数以获得真实的函数值 y next y_{\text{next}} ynext。
  6. 更新数据并重复 ：将 ( x next x_{\text{next}} xnext, y next y_{\text{next}} ynext) 添加到观测数据集中，并返回步骤 2。

当我们调优像 CNN 这样的复杂模型时，步骤 5 的计算成本很高。

贝叶斯优化试图通过有效地搜索下一个要测试的最佳组合来最小化步骤 5 的运行次数。

最佳使用场景：

  • 昂贵的目标函数：非常适合单个训练运行和评估非常耗时的模型（例如，深度神经网络）。
  • 有限的评估预算：需要以最少的试验次数找到最优超参数。
  • 复杂且非凸的搜索空间：当超参数和模型性能之间的关系是非线性且难以手动导航，存在许多局部最优解，搜索算法可能陷入其中。

局限性：

  • 实现起来可能比网格搜索或随机搜索更复杂。
  • 由于需要维护和更新代理模型，每次迭代的计算开销更高。
  • 在非常高维的超参数空间中可能表现不佳。

6.1 选择代理模型

了解贝叶斯优化如何工作后，我将在本节中探索其代理模型。

除了高斯过程（GPs），贝叶斯优化还可以利用各种代理模型。主要例子包括：

  • 随机森林 (RF)：决策树的集成；适用于混合数据类型，可以从树的方差中估计不确定性。
  • 树结构 Parzen 估计器 (TPE)：对好的和坏的超参数配置的密度进行建模以提出新的点；擅长处理分类和条件空间。
  • 贝叶斯神经网络 (BNN)：由于概率权重，神经网络输出预测的分布，本质上提供了不确定性。
  • 深度核学习 (DKL)：结合神经网络进行特征学习和高斯过程进行鲁棒建模和不确定性量化。
  • 模型集成：使用多个更简单的模型来增强鲁棒性并改进不确定性估计。

代理模型的选择取决于优化问题和搜索空间的特性。例如，

  • 高维搜索空间 ：最佳 ：TPE、BNN、DKL，最差：RF
  • 混合超参数 ：最佳 ：TPE、RF，最差：传统高斯过程
  • 有限计算预算 ：最佳 ：TPE、RF，最差：BNN、DKL
  • 精度要求高的项目 （例如，药物发现项目，其中精确预测是必需的）：最佳 ：传统高斯过程、DKL，最差：TPE、RF

我将在本文中重点介绍高斯过程，因为它具有一般优势：

  • 可靠的不确定性量化
  • 在贝叶斯优化通常遇到的低数据量情况下表现出色。

6.2 高斯过程的数学形式

正如我们之前讨论的，高斯过程是一个概率模型，它生成一个关于所有可能拟合给定数据的函数的分布。

想象我们有三组数据 (x, y)：

  • (1, 2)
  • (2, 4)
  • (3, 3)

以及预测点：x = 2.5

例如，线性回归 试图使用这三个数据点找到一个近似函数，计算当 x = 2.5 x = 2.5 x=2.5 时的预测值 y ^ \hat{y} y^，并根据它们的近似函数（比如）： y ^ = 0.5 x + 2 \hat{y} = 0.5x + 2 y^=0.5x+2 输出一个单一值： y ^ = 3.75 \hat{y} = 3.75 y^=3.75。

另一方面，高斯过程 在预测点生成一个高斯分布而不是单一值。

例如，高斯过程会输出在 x = 2.5 x = 2.5 x=2.5 处的预测值 ∼ N ( μ , σ 2 ) \sim N(\mu, \sigma^2) ∼N(μ,σ2)，其中均值 μ ≈ 3.28 \mu \approx 3.28 μ≈3.28，方差 σ 2 ≈ 0.15 \sigma^2 \approx 0.15 σ2≈0.15。

在数学上，这个输出被概括为后验概率，如下所示：

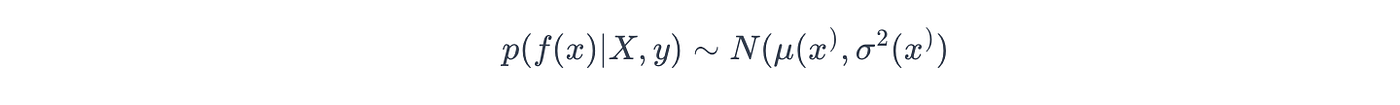
其中 μ ( x ∗ ) \mu(x^*) μ(x∗) 和 σ 2 ( x ∗ ) \sigma^2(x^*) σ2(x∗) 表示给定数据集 (X, y) 时预测点 ( x ∗ x^* x∗) 处的均值/方差函数。

高斯过程的其他关键特征包括：

  • 概率模型 ：在预测点生成一个关于所有可能函数的高斯分布，而不是单个值或标签。
  • 不确定性量化：使用估计高斯分布的方差量化预测中的不确定性（因此，我们可以看到其预测的置信水平）。
  • 多元正态分布 ：假设任何 有限的随机变量集合都具有多元高斯分布，其均值和协方差由均值函数和核（协方差）函数定义。
  • 非参数：不假设具有预定参数数量的固定函数形式。
  • 灵活性：通过选择不同的核函数可以建模各种函数形状。
  • 贝叶斯框架：遵循自然的贝叶斯框架，从先验分布开始，并在观察数据后将先验更新为后验分布。

计算后验概率

利用其遵循贝叶斯框架的特性，高斯过程首先定义其对潜在真实函数 f ( x ) f(x) f(x) 的先验信念，如下所示：

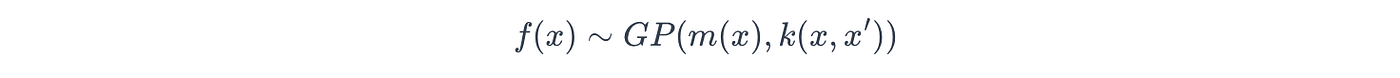
其中：

  • m ( x ) m(x) m(x)：先验均值函数
  • k ( x , x ′ ) k(x, x') k(x,x′)：先验核（协方差）函数。

然后，高斯过程使用此先验计算后验概率。

由于高斯过程假设随机变量服从多元高斯分布 ，目标 y y y 和真实值 f ( x ) f(x) f(x) 的联合先验分布 （同时观察到 y y y 和 f ( x ) f(x) f(x) 的可能性）定义如下：

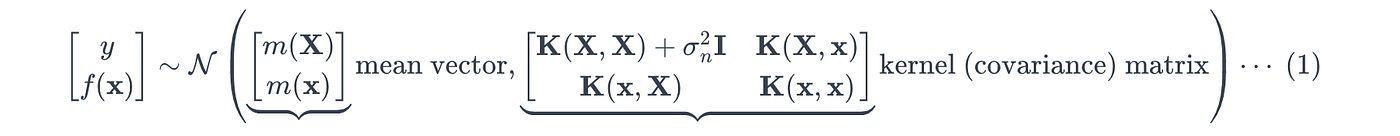
其中：

*对于高斯噪声，高斯过程假设目标变量 y y y 被独立高斯噪声 ϵ \epsilon ϵ 污染，使得：

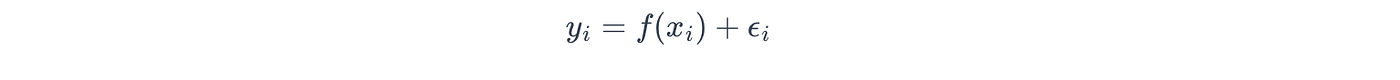
其中噪声是从具有噪声方差 σ n \sigma_n σn 的高斯分布中提取的：

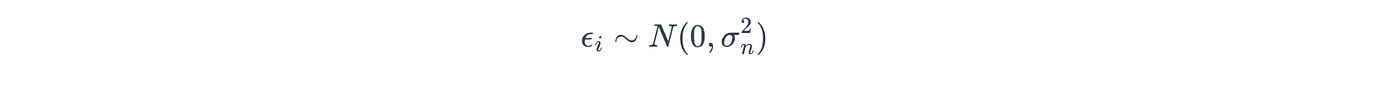
利用多元高斯分布的条件分布性质在公式 (1) 上，高斯过程计算预测点 x ∗ x^* x∗ 处的后验概率，其均值 μ ( x ∗ ) \mu(x^*) μ(x∗) 和方差 σ 2 ( x ∗ ) \sigma^2(x^*) σ2(x∗) 定义如下：

这些方程展示了高斯过程如何根据观测数据调整先验。

特别是， K ( X , X ) + σ n 2 I K(X, X) + \sigma_n^2 I K(X,X)+σn2I 的逆表示观测数据的影响，权衡每个观测对预测的贡献以及方差减少的程度。

在这里，不同的核函数 K 编码了关于底层函数的平滑度、周期性或其他属性的不同假设。这使得高斯过程能够灵活地学习各种函数。

6.3 在搜索空间中寻找下一个评估点

在高斯过程估计后验分布后，贝叶斯优化利用采集函数 计算每个 搜索点的效用分数，使用高斯过程估计的均值和方差。

贝叶斯优化中常用的采集函数之一是预期改进 (EI)：

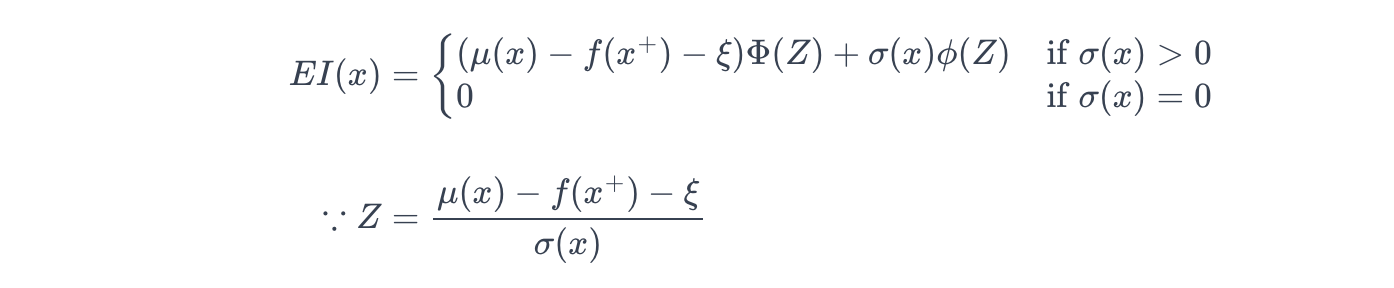
其中：

  • μ ( x ) \mu(x) μ(x)：高斯过程给出的点 x 处的预测均值
  • f ( x + ) f(x^+) f(x+)：当前最佳值
  • ξ ≥ 0 \xi \geq 0 ξ≥0：探索-利用权衡参数。较大的 ξ \xi ξ 鼓励更多的探索，而 ξ = 0 \xi = 0 ξ=0 则纯粹关注最大化预期收益。
  • μ ( x ) − f ( x + ) \mu(x) - f(x^+) μ(x)−f(x+)：相对于当前最佳的预测改进。
  • μ ( x ) − f ( x + ) − ξ \mu(x) - f(x^+) - \xi μ(x)−f(x+)−ξ：在考虑点 x 时潜在的收益。
  • σ ( x ) \sigma(x) σ(x)：高斯过程给出的点 x 处的预测标准差。
  • Z Z Z：一个标准化分数（z-score），通过不确定性对潜在收益进行归一化。
  • Φ ( Z ) \Phi(Z) Φ(Z) / ϕ ( Z ) \phi(Z) ϕ(Z)：在 Z 处评估的标准正态分布的累积分布函数 (CDF) / 概率密度函数 (PDF)。

当点 x 处没有不确定性时（因此 σ ( x ) = 0 \sigma(x) = 0 σ(x)=0），EI 值为零，因为没有进一步预期收益的潜力。

相反，当存在不确定性时 ( σ ( x ) > 0 \sigma(x) > 0 σ(x)>0)，EI 根据相对于当前最佳的预测改进计算点 x 处的潜在收益，同时使用 ξ \xi ξ 平衡探索和利用。

因此，更高的 EI(x) 值意味着当系统接下来探索 x 时，x 具有更大的预期收益。

贝叶斯优化会选择这样的点进行下一步探索。

6.4 搜索空间

与随机搜索类似，贝叶斯优化受益于广阔的搜索空间，这主要是因为广阔的搜索空间显著降低了错过真正全局最优解的风险。

其由高斯过程引导的探索-利用平衡使其能够有效地识别有前景的区域，即使在广阔的超参数空间中也是如此。

因此，我为贝叶斯优化使用了与随机搜索相同的搜索空间。

6.5 模拟

我利用 Keras-Tuner 库中的 BayesianOptimization 类，进行了五次试验，每次包含 50 个子集，以解决其随机性。我取了平均和最佳 MAE。

python 复制代码 
import time  
import keras_tuner as kt

  
max_trials = 50  
tuner = kt.BayesianOptimization(  
    hypermodel=build_cnn_model_keras,  
    objective=kt.Objective("val_mae", direction="min"),   
    max_trials=max_trials,  
    executions_per_trial=1,  
    overwrite=True,  
    directory="my_tuning_dir",    
    project_name="cnn_bayesian_tuning"  
)

  
start_tuning_time = time.time()  
tuner.search(X_train, y_train, epochs=50, validation_data=(X_val, y_val))  
end_tuning_time = time.time()

  
best_model = tuner.get_best_models(num_models=1)[0]  
best_trial = tuner.oracle.get_best_trials(num_trials=1)[0]  
best_hparams = best_trial.hyperparameters  
best_mae = best_trial.metrics.get_last_value('val_mae')  
total_time = end_tuning_time - start_tuning_time  
eval_count = max_trials  
return best_mae, eval_count, total_time, best_hparams, best_model

6.6 结果

贝叶斯优化略低于随机搜索的表现，完成一次包含 50 次测试的试验需要 661 秒（约 11 分钟）。

然而，这种方法在手动和网格搜索方法之间提供了平衡。增加试验次数和每次试验的测试数量可以进一步提高性能。

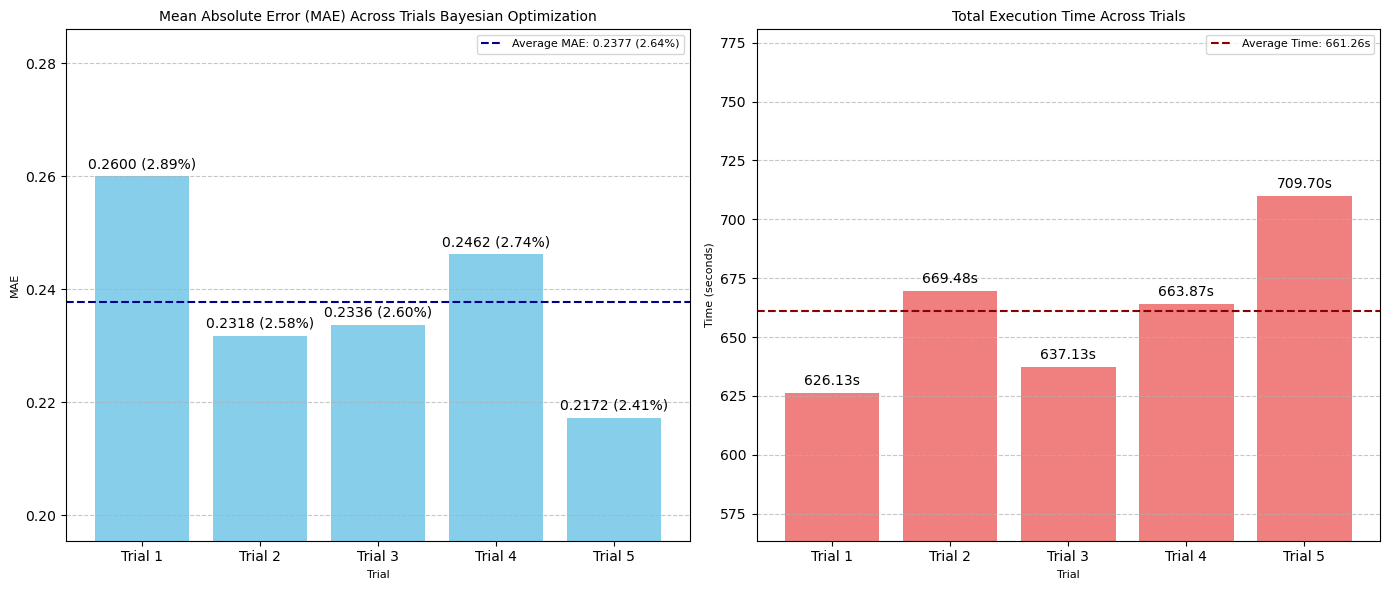
图：五次贝叶斯优化试验中 MAE（左）和搜索时间（秒）（右）的比较

  • 最佳 MAE：0.2172 像素（2.41% 误差范围）
  • 平均 MAE：0.2377 像素（2.64% 误差范围）/ 试验
  • 平均执行时间：661.26 秒 / 试验
  • 评估总数：50 次 / 试验
  • 最佳超参数集 ：
    num_conv_layers: 1, dropout: 0, dense_units: 32, learning_rate: 0.0001, epochs: 1000, filters_0: 16, batch_norm_0: False

7. 元启发式算法

元启发式算法是用于解决传统方法难以或不可能解决的复杂问题的优化技术，尤其是在处理极其庞大的搜索空间时。

它们不 保证找到全局最优解，但旨在在合理的时间内找到一个"足够好"（次优）的解。

其主要特点包括：

  • 受自然/启发式启发：受自然现象、生物过程或人类行为启发。
  • 随机性：在其搜索过程中包含随机性，探索解决方案空间的不同部分，避免陷入局部最优（因此，擅长处理非常规搜索空间）。
  • 探索与利用的平衡：像贝叶斯优化一样，平衡探索和利用。
  • 问题独立性：通过最小的修改即可适用于各种优化问题。
  • 迭代过程：通过多代（迭代）细化一组候选解。
  • 适应度函数：使用适应度函数（目标函数）评估每个候选解（在我们的案例中是超参数集）的质量。

最佳使用场景：

  • 高度复杂、非凸和不连续的搜索空间：当传统的基于梯度的方法不适用或无法有效找到全局最优解时。
  • 全局优化至关重要：需要探索各种解决方案并避免陷入局部最优。

局限性：

  • 计算密集。
  • 性能可能取决于其自身模型参数的调优。

7.1 元启发式算法如何工作

以下是简化步骤：

  1. 初始化 ：在问题搜索空间内随机生成一组初始候选解（称为种群）。
  2. 评估 ：使用目标函数评估每个候选解的适应度。
  3. 更新/改进 ：通过应用其底层隐喻启发的特定规则，生成具有更好适应度值的新、可能更好的种群。该过程包括：
  • 变异：随机变异现有解决方案以引入多样性。
  • 交叉：组合好的解决方案的部分以创建新的解决方案。
  • 移动：粒子或代理根据自己的最佳经验在搜索空间中移动。
  • 接受准则：决定是否接受新解决方案（尤其是在早期阶段，以促进探索）。

4. 选择：选择最佳种群，同时淘汰适应度较低的解决方案。

5. 终止 ：重复步骤 2 到 4 直到收敛。

7.2 元启发式算法的类型

元启发式算法可以根据其灵感大致分类：

进化算法 (EAs)：受生物进化和自然选择启发。

  • 遗传算法：模仿变异、交叉和选择等过程来进化解决方案。
  • 差分进化：使用向量差来创建新的候选解。
  • 进化策略：侧重于变异参数的自适应。

群智能 (SI) 算法：受分散、自组织系统的集体行为启发。

  • 粒子群优化：模拟鸟群或鱼群的社会行为。
  • 蚁群优化：基于蚂蚁寻找食物最短路径的觅食行为。
  • 人工蜂群：模拟蜜蜂群的智能觅食行为。

基于物理的算法：受物理现象启发。

  • 模拟退火：类似于冶金中的退火过程，材料被加热然后缓慢冷却以减少缺陷。
  • 引力搜索算法：基于万有引力定律和质量相互作用。

基于人类的算法：受人类行为或社会互动启发。

  • 禁忌搜索：使用"禁忌列表"以避免重复访问以前探索过的解决方案。
  • 教与学优化：模仿课堂中的教与学过程。

7.3 搜索空间

与贝叶斯优化和随机搜索类似，为元启发式算法设置广阔的搜索空间是有益的，因为它可以定义初始种群和后续世代的更大多样性。

这将使它们能够更广泛地探索并逃离局部最优。

因此，我使用了与随机搜索和贝叶斯优化相同的广阔搜索空间。

7.4 模拟

在这里，我将以一种常见的元启发式算法------遗传算法 (GA) 为例。

遗传算法模仿自然选择来进化物种。

在超参数调优中，"物种"是超参数组合的种群，它们通过偏爱"存活率更高"的个体（在我们的案例中表示更好的 MAE）来随代进化。

让我们一步一步地探索它的迭代方法。

7.4.1 步骤 1. 初始化：创建种群

我设置了一个包含十个个体的初始种群：

python 复制代码 
import random

  
def create_individual():  
    hparams = dict()

      
    hparams['num_conv_layers'] = random.choice(hparams_options['num_conv_layers'])  
    for i in range(hparams['num_conv_layers']):  
        hparams[f'filters_{i}'] = random.choice(hparams_options[f'filters_{i}'])  
        hparams[f'batch_norm_{i}'] = random.choice(hparams_options[f'batch_norm_{i}'])  
    hparams['dense_units'] = random.choice(hparams_options['dense_units'])  
    hparams['epochs'] = random.choice(hparams_options['epochs'])

      
    hparams['learning_rate'] = random.uniform(hparams_options['learning_rate'][0], hparams_options['learning_rate'][-1])  
    hparams['dropout'] = random.uniform(hparams_options['dropout'][0], hparams_options['dropout'][-1])

        return hparams

  
population_size = 10  
population = [create_individual() for _ in range(population_size)]

7.4.2 步骤 2. 评估：计算适应度分数

接下来，计算了种群中所有个体的适应度分数，并选择了表现最佳的个体：

python 复制代码 
eval_count = 0  
total_time = 0.0

best_mae = float('inf')  
best_hparams = None  
best_model = None  
n_generations = 10

for _ in range(n_generations):  
    fitnesses = list()

      
    for indiv in population:  
        eval_count_returned, total_time_returned, mae, model = evaluate_model(hparams=indiv)  
        fitnesses.append(accuracy)  
        eval_count += eval_count_returned  
        total_time += total_time_returned

    current_best_idx = np.argmin(fitnesses)  
    current_best_mae = fitnesses[current_best_idx]  
    current_best_params = population[current_best_idx]

      
    if current_best_mae < best_mae:  
        best_mae = current_best_mae  
        best_params = current_best_params  
        best_model = model

7.4.3 步骤 3: 迭代

在迭代循环中，遗传算法通过选择适应度分数最高的 10%（或您选择的任何百分比）的高表现者（elites）来构建新种群。

我选择了 MAE 最低的最佳个体：

python 复制代码 
import numpy as np

  
new_population = []

  
num_elites = max(1, int(0.1 * population_size))  
elites = sorted(zip(population, fitnesses), key=lambda x: x[1], reverse=False)[:num_elites]  
new_population.extend([e[0] for e in elites])

然后，通过生成九个变异的后代来更新十个个体的种群：

python 复制代码 
import random

  
num_parentes_to_select = population_size - num_elites  
total_fitness = sum(fitnesses)  
probabilities = [f / total_fitness for f in fitnesses]  
indices = np.random.choice(  
    len(population),   
    size=num_parentes_to_select,   
    p=probabilities,   
    replace=True  
)  
parents = [population[i] for i in indices]

  
def crossover(parent1, parent2, crossover_rate):  
    offspring1 = parent1.copy()  
    offspring2 = parent2.copy()  
    if random.random() < crossover_rate:  
        offspring1['num_conv_layers'] = random.choice([parent1['num_conv_layers'], parent2['num_conv_layers']])  
        offspring2['num_conv_layers'] = random.choice([parent1['num_conv_layers'], parent2['num_conv_layers']])  
    for param in ['dense_units', 'dropout', 'learning_rate', 'epochs']:  
        if random.random() < crossover_rate:  
            offspring1[param], offspring2[param] = parent2[param], parent1[param]

        for offspring in [offspring1, offspring2]:  
        for i in range(offspring['num_conv_layers']):  
            if f'filters_{i}' not in offspring:  
                offspring[f'filters_{i}'] = random.choice(hparams_options['filters_0'])  
            if f'batch_norm_{i}' not in offspring:  
                offspring[f'batch_norm_{i}'] = random.choice(hparams_options['batch_norm_0'])  
    return offspring1, offspring2

  
def mutate(individual):  
    mutated_individual = individual.copy()

        if random.random() < mutation_rate:  
        mutated_individual['num_conv_layers'] = random.choice(hparams_options['num_conv_layers'])  
        for i in range(max(hparams_options['num_conv_layers'])):  
            if i < mutated_individual['num_conv_layers']:  
                if f'filters_{i}' not in mutated_individual or random.random() < mutation_rate:  
                    mutated_individual[f'filters_{i}'] = random.choice(hparams_options['filters_0'])  
                if f'batch_norm_{i}' not in mutated_individual or random.random() < mutation_rate:  
                    mutated_individual[f'batch_norm_{i}'] = random.choice(hparams_options['batch_norm_0'])  
            else:  
                mutated_individual.pop(f'filters_{i}', None)  
                mutated_individual.pop(f'batch_norm_{i}', None)  
    if random.random() < mutation_rate:  
        mutated_individual['dense_units'] = random.choice(hparams_options['dense_units'])  
    if random.random() < mutation_rate:  
        mutated_individual['dropout'] = random.uniform(hparams_options['dropout'][0], hparams_options['dropout'][-1])  
    if random.random() < mutation_rate:  
        mutated_individual['learning_rate'] = random.uniform(hparams_options['learning_rate'][0], hparams_options['learning_rate'][-1])  
    if random.random() < mutation_rate:  
        mutated_individual['epochs'] = random.choice(hparams_options['epochs'])  
    return mutated_individual

  
crossover_rate = 0.8  
mutation_rate = 0.1  
for i in range(0, len(parents), 2):  
    if len(new_population) >= population_size: break

      
    parent1 = parents[i]  
    parent2 = parents[i+1]  
    offspring1, offspring2 = crossover(parent1, parent2, crossover_rate)

          
    new_population.append(mutate(offspring1))  
    if len(new_population) < population_size: new_population.append(mutate(offspring2))

      
while len(new_population) < population_size:  
    new_population.append(mutate(random.choice(elites)[0]))

  
population = new_population

7.4.4 步骤 4 & 5: 选择最佳参数

我重复这个过程五代，每代创建十个组合（个体）：

python 复制代码 
n_generations = 5

for _ in range(n_generations):  
      
    fitnesses = list()  
    for indiv in population:  
        eval_count_returned, total_time_returned, mae, model = evaluate_model(hparams=indiv)  
        fitnesses.append(accuracy)  
        eval_count += eval_count_returned  
        total_time += total_time_returned

    current_best_idx = np.argmin(fitnesses)  
    current_best_mae = fitnesses[current_best_idx]  
    current_best_params = population[current_best_idx]

    if current_best_mae < best_mae:  
        best_mae = current_best_mae  
        best_params = current_best_params  
        best_model = model

      
    new_population = []  
    num_elites = max(1, int(0.1 * population_size))  
    elites = sorted(zip(population, fitnesses), key=lambda x: x[1], reverse=False)[:num_elites]  
    new_population.extend([e[0] for e in elites])  
    num_offspring = population_size - num_elites  
    parents = select_parents(population, fitnesses, num_offspring)

    for i in range(0, len(parents), 2):  
        if len(new_population) >= population_size: break  
        parent1 = parents[i]  
        parent2 = parents[i+1]  
        offspring1, offspring2 = crossover(parent1, parent2, crossover_rate)  
        new_population.append(mutate(offspring1))  
        if len(new_population) < population_size: new_population.append(mutate(offspring2))

    while len(new_population) < population_size:  
        new_population.append(mutate(random.choice(elites)[0]))

    population = new_population

return best_mae, eval_count, total_time, best_hparams, best_model

7.5 结果

遗传算法表现出广泛的性能范围，产生了 2.36% 的最佳误差范围，超过了网格搜索，并且以**最有效的时间成本（188 秒，约 3 分钟）**完成了 50 次 CNN 测试。

然而，其最差误差范围（第二次试验时为 3.67%）是所有方法和试验中最高的。

这表明遗传算法固有的随机性，它比网格搜索等方法更动态、更不系统地探索搜索空间。

虽然这允许逃离局部最优，但它也可能导致不同运行或试验的性能和收敛速度的可变性。

在我们的案例中，由于第二次试验，遗传算法的平均 MAE 在四种自动化方法中是最高的。

运行更多试验并增加世代数可能会带来更好的结果。

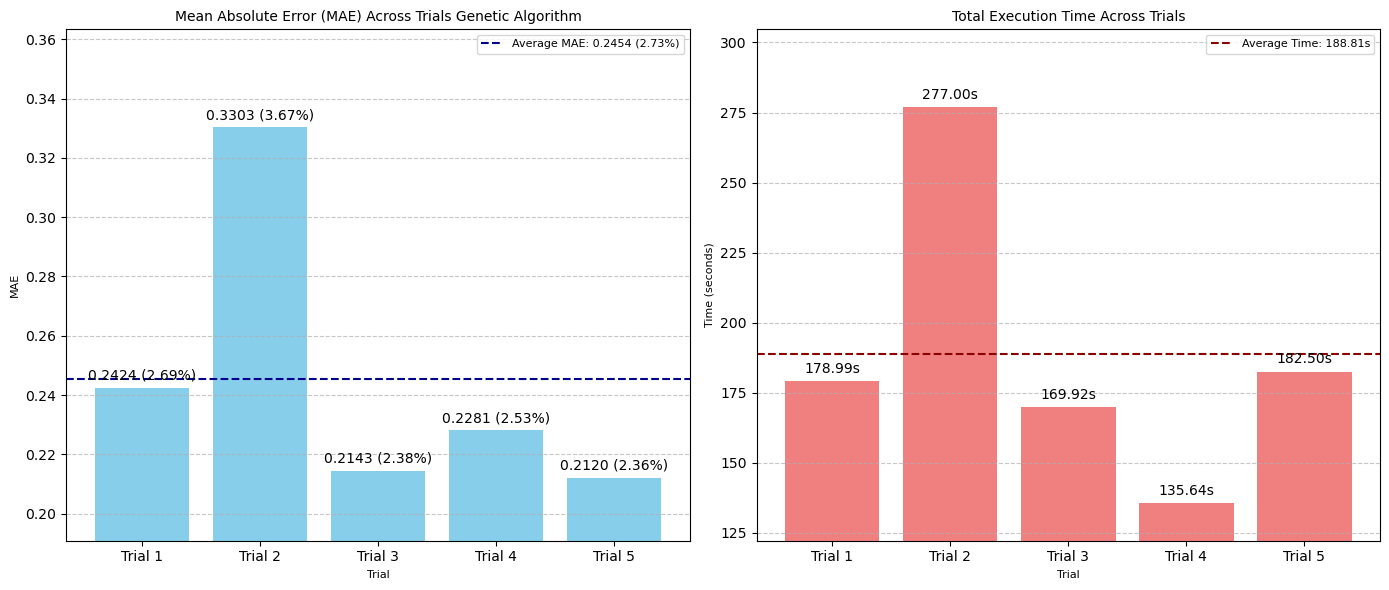
图：五次遗传算法试验中 MAE（左）和搜索时间（秒）（右）的比较（

  • 最佳 MAE：0.2120 像素（2.36% 误差范围）
  • 平均 MAE：0.2454 像素（2.73% 误差范围）/ 试验
  • 平均执行时间：188.81 秒 / 试验
  • 评估总数：50 次 / 试验
  • 最佳超参数集 ：
    num_conv_layers: 1, dropout: 0, dense_units: 32, learning_rate: 0.0001, epochs: 1000, filters_0: 16, batch_norm_0: False

8. 泛化能力和时间效率的最终评估

在评估这五种方法时，泛化性能 （通过测试数据集上的 MAE 衡量）是最关键的指标，它表明模型在未见过数据上的表现能力。

然后，时间效率也是一个重要的考虑因素，尤其是在计算资源有限的情况下。

下表展示了所有五种方法的平均和最佳结果以及我实施的搜索策略摘要：

图：超参数调优方法在 CNN 上的性能比较和搜索策略（泛化：测试数据集上的 MAE 分数，总时间：总搜索时间（秒），平均时间：每次评估的平均时间（秒）（总时间/评估次数））

8.1 泛化能力

在自动化方法中，随机搜索 和贝叶斯优化实现了最佳的泛化性能，误差率约为 2.53%。

它们强大的泛化能力得到了进一步支持，即搜索期间的最佳 MAE 与其泛化 MAE 之间的差异极小。

相比之下，遗传算法 显示出轻微的过拟合倾向，其搜索误差率与泛化误差率之间存在 0.35 个百分点的差距。

网格搜索虽然比手动搜索有所改进，但最终泛化能力最差，这表明扩大其搜索空间可以提高性能。

8.2 时间效率

在时间效率方面，遗传算法被证明是最有效的自动化方法，每次评估的平均时间为 3.65 秒，50 次评估的总时间为 182.50 秒。

随机搜索也非常高效，平均时间为 4.10 秒，总时间为 205.04 秒。

相比之下，贝叶斯优化尽管具有竞争性的泛化能力，但时间效率最低，每次评估的平均时间为 14.19 秒，总时间高达 709.70 秒。

这表明了贝叶斯优化的本质。它旨在样本高效 ，需要更少的昂贵目标函数的实际评估，但引入了与构建和优化概率代理模型（高斯过程）相关的自身计算开销。

当单个目标函数不那么昂贵时，这种开销可能使总时间比随机搜索等更简单的方法更长。

总之，对于本次实验，随机搜索在泛化和时间效率方面都取得了最佳结果。

9. 针对表格数据上训练的简单模型

现在，在理解了每种方法在复杂模型上的表现后，本节将探讨相同的五种方法在更简单的模型上，即在包含 3,000 个数据点的表格数据集上训练的核 SVM：

9.1 表格数据

我从一个包含 10 个特征的 3,000 个合成表格数据集创建了训练、验证和测试数据集：

python 复制代码 
import numpy as np  
from sklearn.model_selection import train_test_split

n_samples = 10000  
n_features = 10  
test_size = 1000  
random_state = 42  
np.random.seed(random_state)

X = np.zeros((n_samples, n_features))  
X[:, 0] = np.random.uniform(-5, 5, n_samples)  
X[:, 1] = np.random.normal(0, 3, n_samples)  
X[:, 2] = np.random.uniform(-10, 10, n_samples)  
if n_features > 3: X[:, 3] = np.random.normal(5, 2, n_samples)

y = np.zeros(n_samples)  
y += 2 * X[:, 0] + 5  
y += 0.5 * (X[:, 1] ** 2) - 3 * X[:, 1]  
y += 10 * np.sin(X[:, 2] / 2)  
y += 0.7 * X[:, 0] * X[:, 3]  
noise = np.random.normal(0, 2, n_samples) * (1 + 0.1 * np.abs(X[:, 0]))  
y += noise

  
X_tv, X_test, y_tv, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state)  
X_train, X_val, y_train, y_val = train_test_split(X_tv, y_tv, test_size=test_size, random_state=random_state)

  
from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()  
X_train = scaler.fit_transform(X_train)  
X_val = scaler.transform(X_val)  
X_test = scaler.transform(X_test)  
print(X_train.shape, y_train.shape, X_val.shape, y_val.shape, X_test.shape, y_test.shape)

(8000, 10) (8000,) (1000, 10) (1000,) (1000, 10) (1000,)

目标变量的范围：[-51.58330487465222, 125.96875771528616]

9.2 搜索空间

与 CNN 案例采取类似策略，我为随机搜索、贝叶斯优化和遗传算法定义了一个更广阔的搜索空间，其中包含离散和连续选项：

python 复制代码 
hparams_options = {  
      
    'kernel': ['linear', 'poly', 'rbf', 'sigmoid'],  
    'gamma': ['auto', 'scale', 1, 0.1, 0.05, 0.01, 0.001],  
    'max_iter': [i for i in range(50, 3001)],

      
    'tol': [0.1, 0.0001],  
    'coef0': [0.1, 1.0],  
    'C': [0.1, 10],  
    'epsilon': [0.1, 0.0001],  
}

对于网格搜索，将搜索空间缩小到只有离散选项：

python 复制代码 
hparams_options = {  
    'kernel': ['linear', 'poly', 'rbf', 'sigmoid'],  
    'gamma': ['auto', 'scale', 1, 0.1, 0.05, 0.01, 0.001],  
    'max_iter': [100, 300, 500]  
    'tol': [0.01, 0.001],  
    'C': [0.1, 1, 10],  
    'epsilon': [0.001, 0.0001],  
}

注意：核 SVM 比 CNN 简单得多，超参数组合数量有限。在广阔的搜索空间中运行网格搜索可能是一个选择。

9.3 评估模型

虽然是可选的，但建议对更简单的 Scikit-learn 模型使用 K 折交叉验证，以确保在未见过的数据上获得稳定的性能。

我定义了 build_evaluate_model 函数来处理每个模型的构建、训练和评估，循环五折：

python 复制代码 
import time  
from sklearn.svm import SVR  
from sklearn.model_selection import KFold  
from sklearn.metrics import mean_absolute_error

def build_evaluate_model(hparams: dict, eval_count: int = 0, total_time: float = 0.0, n_splits: int = 5) -> tuple:  
    kernel = hparams.get('kernel', 'rbf')  
    degree = hparams.get('degree', 3)  
    gamma = hparams.get('gamma', 'scale')  
    coef0 = hparams.get('coef0', 0)  
    tol = hparams.get('tol', 0.001)  
    C = hparams.get('C', 1)  
    epsilon = hparams.get('epsilon', 0.1)  
    max_iter = hparams.get('max_iter', 100)  
    start_time = time.time()

      
    maes = 0  
    kf = KFold(n_splits=n_splits, shuffle=True, random_state=42)  
    for train_index, val_index in kf.split(X_train):  
        X_train_fold, X_val_fold = X_train[train_index], X_train[val_index]  
        y_train_fold, y_val_fold = y_train[train_index], y_train[val_index]

          
        model = SVR(  
            kernel=kernel,  
            degree=degree,  
            gamma=gamma,  
            coef0=coef0,  
            tol=tol,  
            C=C,  
            epsilon=epsilon,  
            max_iter=max_iter,  
            verbose=False,   
        ).fit(X_train_fold, y_train_fold)

          
        y_pred_val_kf = model.predict(X_val_fold)  
        maes += mean_absolute_error(y_pred_val_kf, y_val_fold)  
        eval_count += 1

    end_time = time.time()  
    total_time += (end_time - start_time)  
    ave_mae = maes / n_splits  
    return eval_count, total_time, ave_mae

9.4 结果

结果表明，随着采用更先进的优化策略，模型性能有所提高；贝叶斯优化 在泛化误差方面表现最佳（MAE: 2.4710，1.39% 误差范围）。

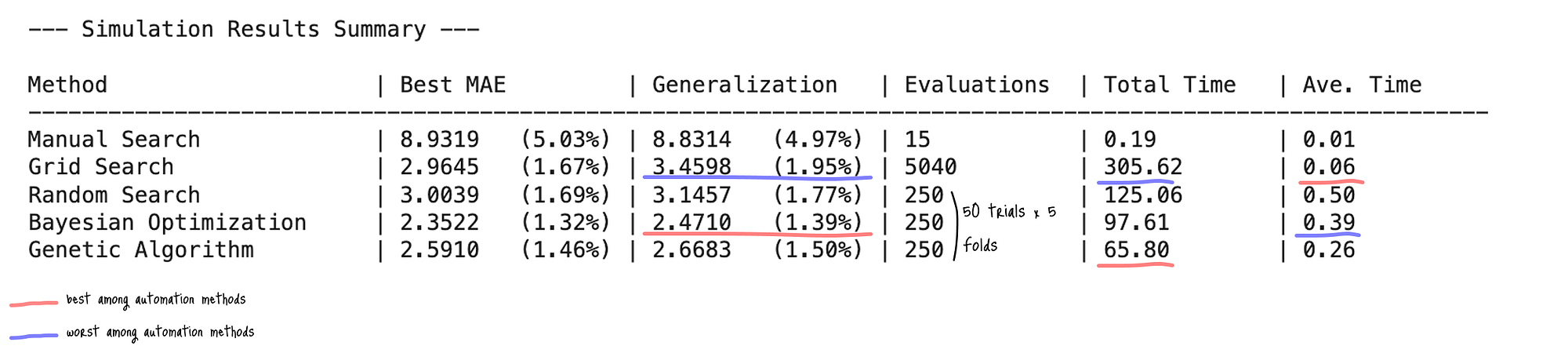
图：超参数调优方法在 核 SVM 上的性能比较（泛化：测试数据集上的 MAE 分数，()：误差范围，总时间：总搜索时间（秒），平均时间：每次评估的平均时间（秒）（总时间/评估次数））

现在，让我们看看每种方法的性能。

9.4.1 手动搜索

手动搜索虽然计算量最小，但预测精度最差（MAE 为 8.8314 / 4.97% 误差范围），突出了其有效超参数调优的局限性。

最佳超参数集：

  • kernel: 'linear'
  • gamma: 0.1
  • tol: 0.01
  • coef0: 1.0
  • C: 1.0
  • epsilon: 0.1
  • max_iter: 50

9.4.2 网格搜索

网格搜索在 MAE (3.4598 / 1.95% 误差范围) 方面比手动调优有了显著改进。

然而，其穷尽搜索导致了大量的评估次数（5,040 = 1,008 模式 x 5 折 ）和最长的实际执行时间（305.62 秒），这使得它对于更大的搜索空间来说效率低下。

最佳超参数集：

  • kernel: "rbf"
  • gamma: 1
  • tol: 0.01
  • coef0: 0
  • C: 10
  • epsilon: 0.0001
  • max_iter: 500

9.4.3 随机搜索

随机搜索在其他随机搜索方法中产生了中等结果，误差范围为 1.77% ，经过 250 次评估（50 模式 x 5 折）。

与网格搜索相比，它在性能和执行时间方面都有所改进，使用的搜索次数更少（250 次 vs 5,040 次）。

最佳超参数集：

  • kernel: "rbf"
  • gamma: 1
  • tol: 0.018670512147205817
  • coef0: 0.24733542330773028
  • C: 2.802020727787644
  • epsilon: 0.0063082312071634505
  • max_iter: 1,512

9.4.4 贝叶斯优化 (Scikit-Optimize)

贝叶斯优化在预测精度方面表现最佳 ，在训练期间生成了最低的 MAE (2.3522) 和强大的泛化能力（MAE: 2.4710 / 1.39% 误差范围）。

它还在自动化方法中实现了最少的评估次数（250 次）。

然而，其概率建模方法使其成为最耗时的方法，导致每次评估的平均时间最高（0.39 秒）。

最佳超参数集：

  • kernel: "rbf"
  • gamma: 0.6283361736403552
  • tol: 0.00061852605407886
  • coef0: 0.15445767772707622
  • C: 10.0
  • epsilon: 0.0009534694901172961
  • max_iter: 3,000

9.4.5 遗传算法

遗传算法在自动化方法中也表现出强大的性能（MAE 为 2.6683 / 1.50% 误差范围 ）。它还在65.8 秒内以最快的速度完成了相同的 250 次搜索。

增加世代数和种群规模可以进一步提高性能。

最佳超参数集：

  • kernel: "rbf"
  • gamma: 1
  • tol: 0.05646743039011411
  • coef0: 0.9662477750994501
  • C: 10
  • epsilon: 0.05000297689759651
  • max_iter: 1,718

总而言之，当考虑计算时间与预测结果之间的权衡 时，遗传算法脱颖而出，提供了最佳平衡，以合理的计算成本提供了强大的性能。

贝叶斯优化虽然实现了最低的 MAE，但每次评估的计算开销更高，这使得当我们将最佳峰值性能置于开销之上时，它是一个不错的选择。

正如我们在 CNN 案例中看到的那样，这种权衡对复杂模型提出了挑战。

但对于像核 SVM 这样计算效率高的表格数据集模型，贝叶斯优化可能是一个绝对的选择，因为每次测试的时间明显更快（0.39 秒）与 CNN（14.2 秒）相比。

10. 结论

在我们的实验中，我们观察到超参数调优方法的效果各不相同。

对于像 SVM 这样的复杂和简单模型，我们的发现表明，像遗传算法这样的高级随机方法能产生最佳性能，平衡了最优结果和计算成本。

总而言之：

  1. 从快速手动搜索开始。
  2. 为了找到全局最优解 ，尤其是在小搜索空间中，尝试网格搜索。
  3. 当次优解足够好或唯一选择时，尝试随机方法：
  • 对于昂贵的目标函数，贝叶斯优化是一种高效的选择，它平衡了计算成本和模型的泛化性能。
  • 对于中等目标函数，随机搜索由于其简单性比贝叶斯优化更高效。
  • 对于非凸、复杂的搜索空间，遗传算法可以有效降低陷入局部最优的风险。

如果计算资源允许，我们的实验建议：

  • 对随机方法进行多次试验以标准化结果，
  • 随后，在具有竞争力的组合中选择最常见的超参数值作为最终模型可能是一个可行的策略，并且
  • 采用混合方法，首先使用随机方法缩小搜索空间，然后应用网格搜索寻找全局最优解。

最终的选择取决于模型复杂度、所需的预测能力以及每个项目中的实际计算限制。

相关推荐
阿里云大数据AI技术2 小时前
Mem0 + Milvus：为人工智能构建持久化长时记忆
人工智能
悟乙己2 小时前
探讨Hyperband 等主要机器学习调优方法的机制和权衡
人工智能·机器学习·超参数·调参
藓类少女2 小时前
【深度学习】重采样（Resampling）
人工智能·深度学习
真上帝的左手2 小时前
26. AI-Agent-Dify
人工智能
在猴站学算法2 小时前
机器学习（西瓜书）第八章 集成学习
人工智能·机器学习·集成学习
加油20192 小时前
机器学习vs人类学习：人类学习如何借鉴机器学习方法？
人工智能·机器学习·迁移学习·费曼学习法·学习金子塔·西曼学习法·斯科特扬学习法
幂简集成explinks2 小时前
腾讯云 DeepSeek API 半价取消后的成本优化实践
人工智能·程序员·设计
动能小子ohhh2 小时前
AI智能体（Agent）大模型入门【2】--基于llamaindx部署本地的聊天模型。
人工智能·python·aigc·ai编程
热门推荐
01conda中设置镜像地址（附所有可换的地址）02UV安装并设置国内源03保姆级教程：手把手教你用Dify实现完美多轮对话（附Chatflow和提示词）04UV 工具安装与国内镜像源配置指南05A股预测还能更准？开源大模型Kronos带你跑通预测+回测全流程06GitHub 镜像站点07突破百度网盘的下载限速，两种方法教会你【超详细】08KGG转MP3工具|非KGM文件|解密音频09教你如何认证 Gemini 教育优惠的二次验证，薅个 1年的 Gemini Pro 会员1046个Nano-banana 精选提示词，持续更新中