【机器学习：逻辑回归】

【逻辑回归】

1、简介

我们知道回归任务一般是处理线性问题的，预测结果是连续的，分类任务是结果是离散的。对于分类问题，在传统的机器学习算法中有很多解决方法，这里讲一下众多思想，其中之一------逻辑回归。
逻辑回归(Logistic Regression)通过将线性回归的输出映射到(0,1)区间，得到一个概率值，通过设定阈值的方式达到分类的效果，在此之中，使用Sigmoid函数将连续值转换为概率值，也即使用Sigmoid映射线性结果到（0，1）之间。

2、激活函数（概率映射）

在逻辑回归中，除了使用sigmoid函数用来激活，还有许多类似于sigmoid函数功能的其他函数。简单介绍一下：

1. 阶跃函数：
   

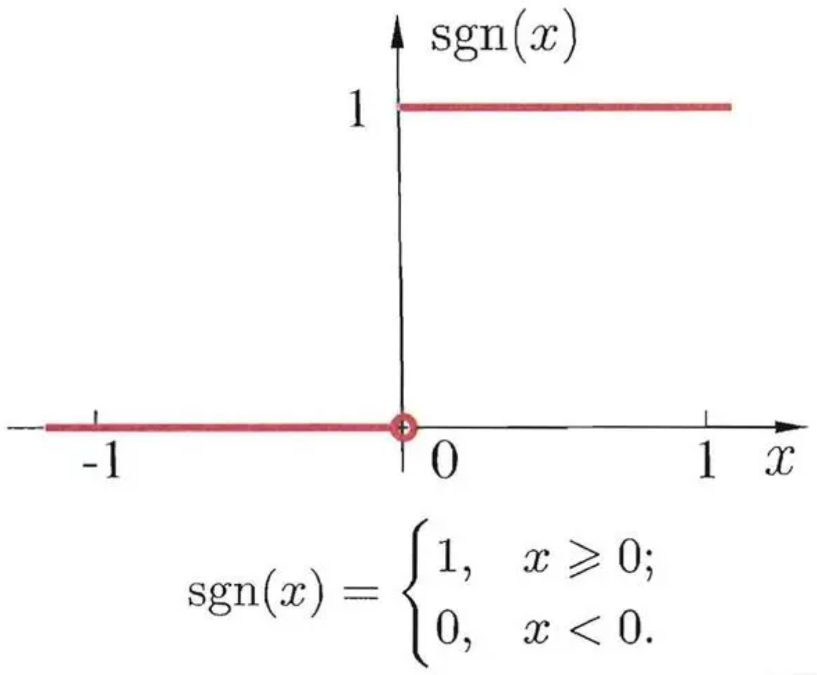
   阶跃函数是间断函数，它可以将大于0的值映射为1，小于0的值映射为0，达到分类的目的。

2. Sigmoid：
   

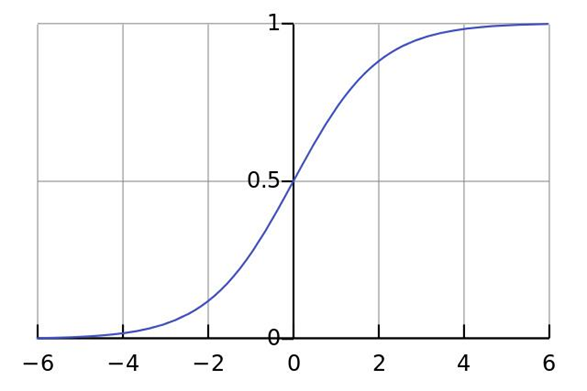
   sigmoid函数图像大致如上，他比阶跃函数更加的平滑，可以将任意的值，线性的映射到 [0, 1] 之间。sigmoid的函数表达式是：
   

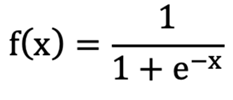
   这个函数求导之后形式非常简单:

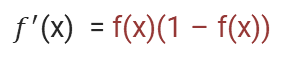
   这个导数公式在计算梯度下降等优化算法时非常有用，因此非常常用。

3. Softmax 函数
   

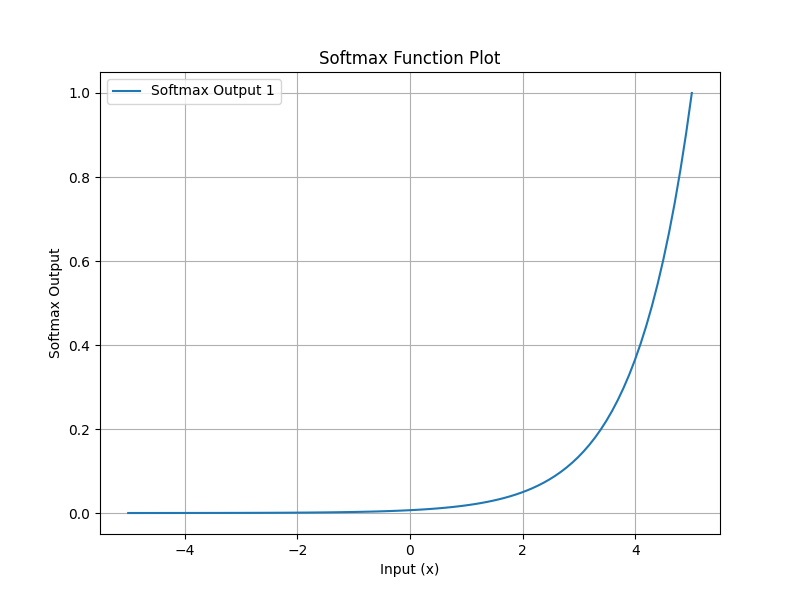
   Softmax 函数是多分类问题中常用的激活函数，尤其在逻辑回归扩展为多项式逻辑回归（Multinomial Logistic Regression）时。与 Sigmoid 相似，Softmax 也能将输出转换为概率，但它能处理多个类别。

   对于一个包含 kkk 个类别的模型，Softmax 函数的输出为：
   

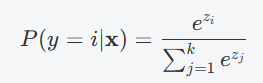
   其中，ziz_izi是每个类别的原始预测值，kkk 是类别总数。Softmax 通过对每个类别的预测值应用指数函数，确保输出的概率之和为 1。

4. ReLU 函数（Rectified Linear Unit）
   

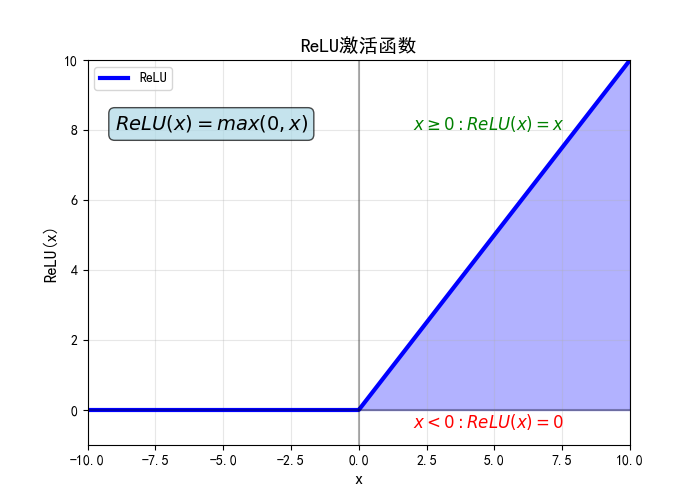
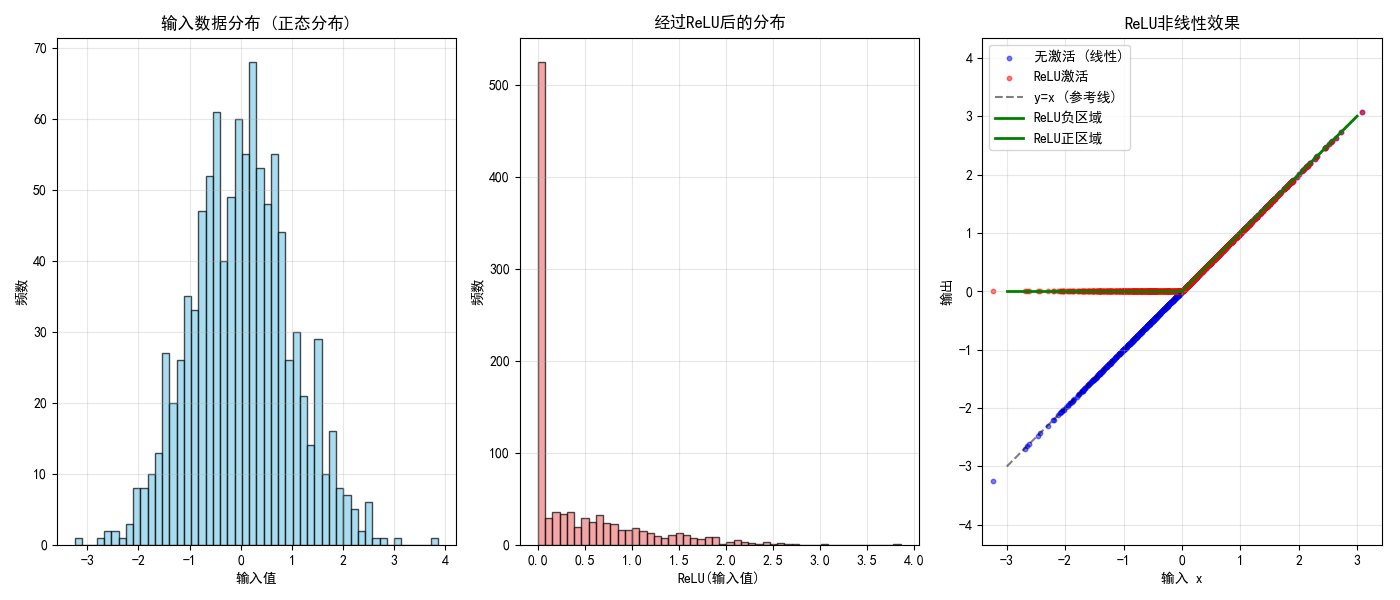
   ReLU 通常用于神经网络的隐藏层，但也可以在某些情况下作为激活函数。ReLU 的输出为输入值本身（对于正数）或者 0（对于负数），即：
   

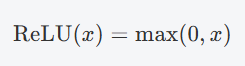
   虽然它不是逻辑回归的标准选择，ReLU 可用于回归任务或者在神经网络架构中使用。不过，如果用于逻辑回归，可能会导致输出没有界限，不再是概率值，且通常用于回归而非分类问题。
   

5. Tanh 函数（双曲正切函数）
   

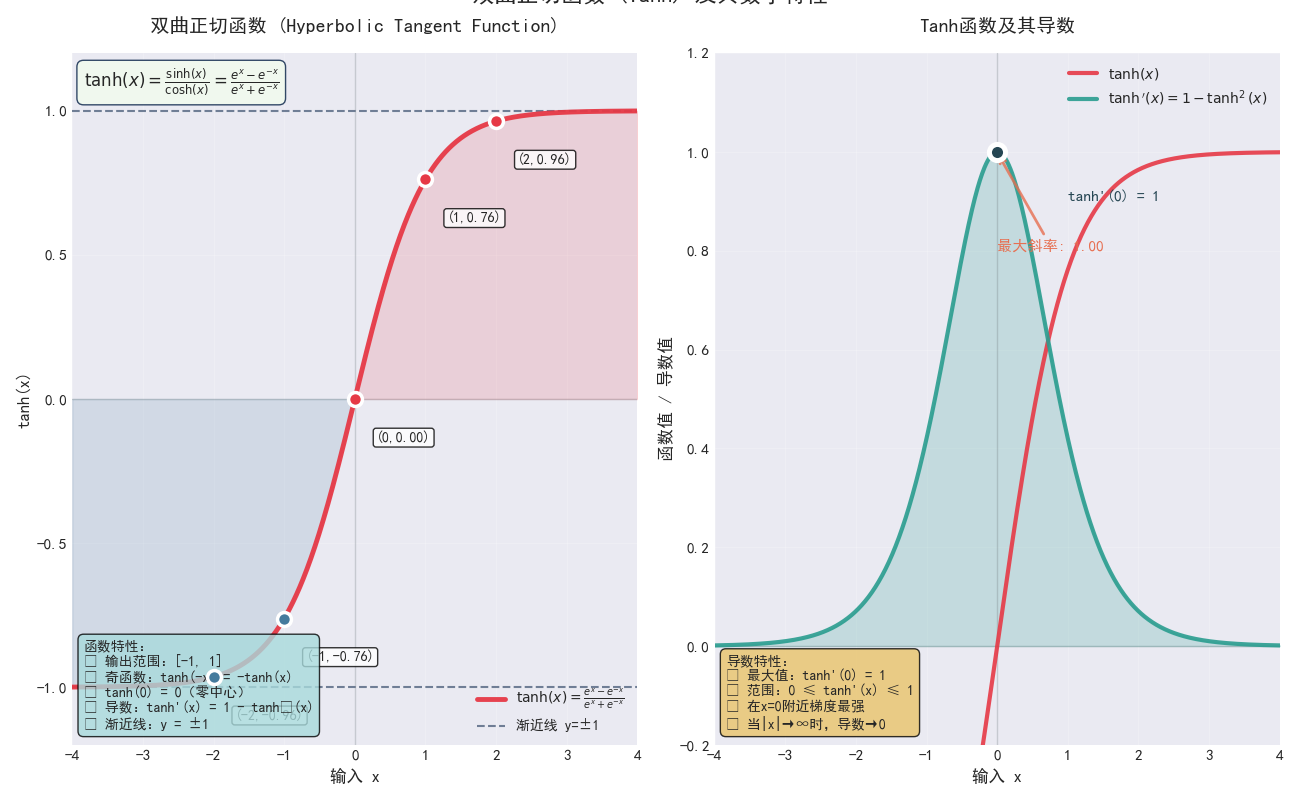
Tanh 函数是 Sigmoid 的一种变体，其输出范围是 [-1, 1]，而 Sigmoid 的输出范围是 [0, 1]，Tanh 函数将输入值压缩到更大的范围，对于输入较大的正负值，输出的梯度较小。

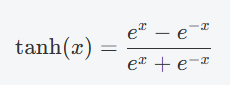
6. Leaky ReLU
   

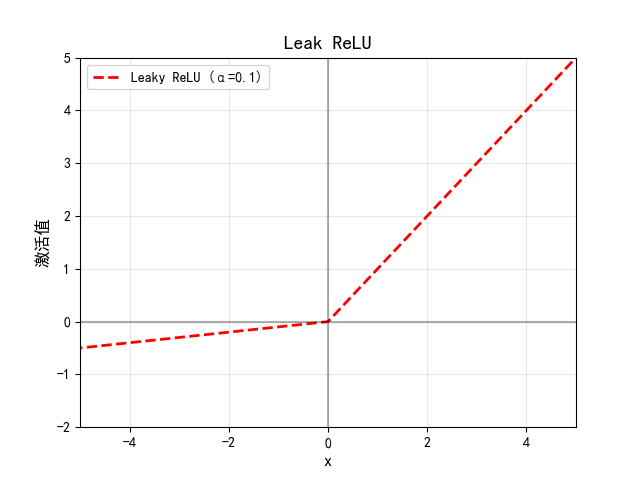
与 ReLU 类似，但允许负数部分输出小的负值。

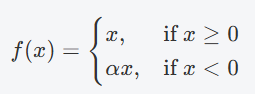
ααα 是一个较小的常数（通常取 0.01 或 0.02），表示在 xxx 为负时允许一部分梯度"泄露"通过。

3、交叉熵损失函数

对于分类问题，没办法像回归问题一样是数据的拟合，我们只是希望预测的结果正确的概率尽量的接近真实概率。分类问题的目标是让模型输出的概率分布接近真实标签的分布，回归问题则是直接让模型输出的数值接近目标值。交叉熵是度量两个概率分布之间差异 的工具；而均方误差（MSE）是度量 两个数值之间距离 的工具。因此，从目标层面上看，交叉熵更符合分类问题的本质。所以对于分类问题，一般情况下都是使用交叉熵损失来衡量误差。

在这里先拿最简单的二分类问题来举例。对于独立同分布的伯努利分布来说，其随机变量只有两种取值：X = 1 （表示"成功"，概率为p）；X = 0（表示"失败"，概率为 1 - p ）

其概率质量函数为：

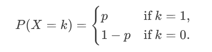
或简写：P(X=k)=pk(1−p)1−k,k∈{0,1}P(X=k) = p^k(1-p)^{1-k}, k\in\{0,1\}P(X=k)=pk(1−p)1−k,k∈{0,1}

假设：有样本[(𝑥1,𝑦1),(𝑥1,𝑦2)...,(𝑥𝑛,𝑦𝑛)][(𝑥_1, 𝑦_1), (𝑥_1, 𝑦_2) ..., (𝑥_𝑛, 𝑦_𝑛) ][(x1,y1),(x1,y2)...,(xn,yn)]，n个样本都预测正确的概率就是伯努利分布的似然函数：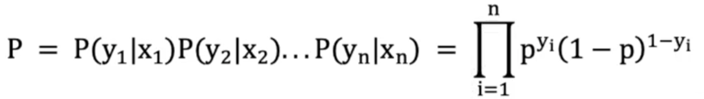
pip_ipi表示每个样本被分类正确时的概率，yiy_iyi 表示每个样本的真实类别（0或1）。

问题转化为：让联合概率事件最大时，估计w、b的权重参数，这就是极大似然估计。

==极大似然估计（Maximum Likelihood Estimation, MLE）==用于从观测数据中估计概率分布的参数。其核心思想是：在已知观测数据的情况下，选择使得这些数据出现概率最大的参数值。

**概率：**固定概率分布参数θθθ，研究随机变量 XXX 的分布。

**似然：**固定观测数据 xxx，研究概率分布参数θθθ的可能性。

要让P最大，对其取负对数，直接得到交叉熵损失：

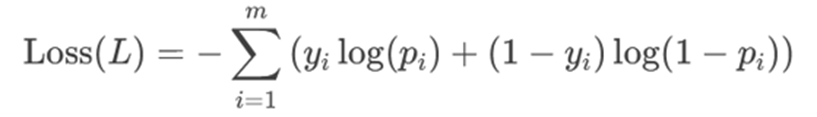
所以，可以理解为伯努利分布的似然函数是逻辑回归交叉熵损失的来源。我们要最大化时间概率（进行极大似然估计），就等价于最小化交叉熵损失。这里为什么要取负对数，其实是为了方便计算，将累乘变成累加，并且实际的极值点位置是不变的。

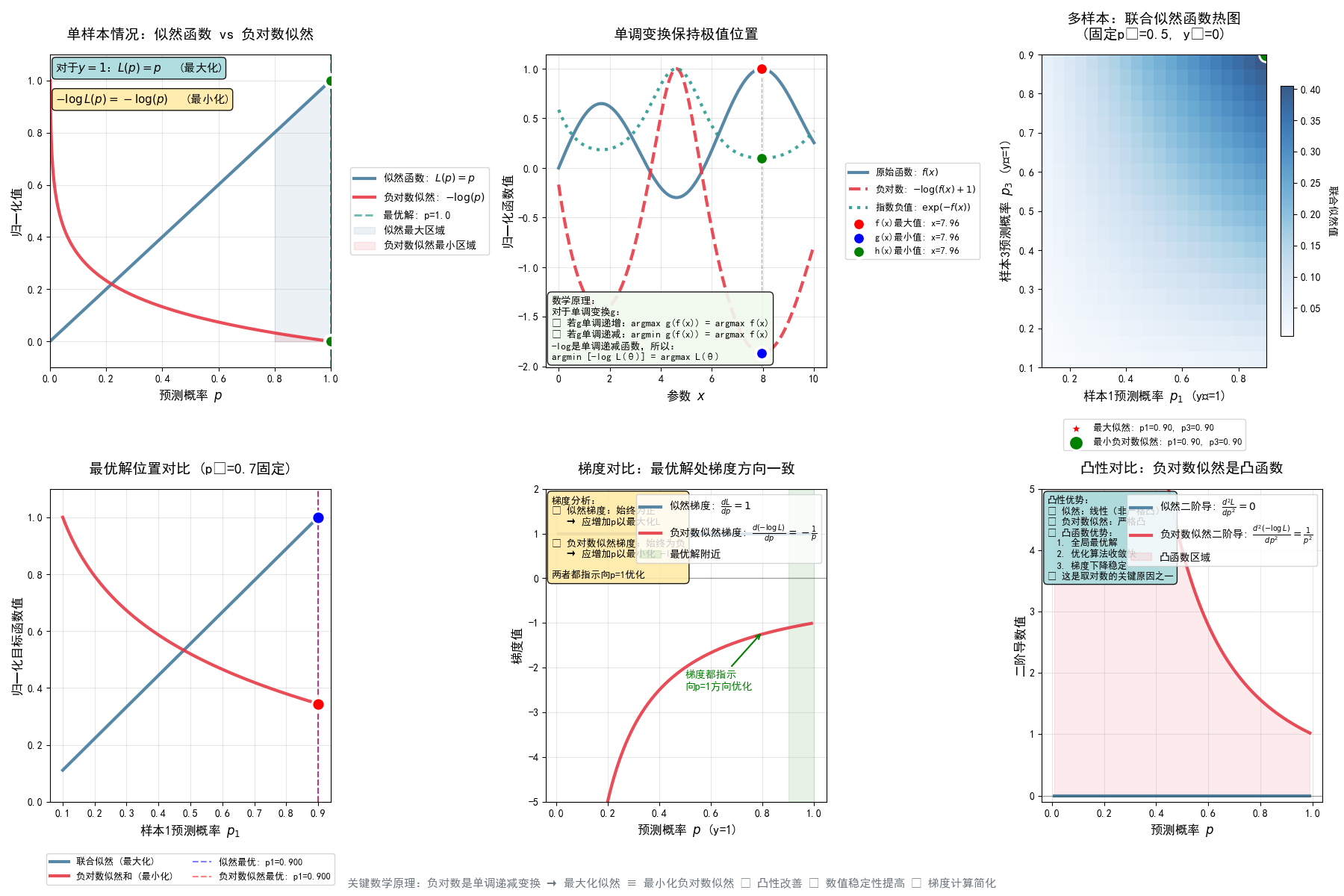
更加简洁的对比例子：

假设已知一个事情发生了（抽到8次黑球，2次白球），求概率分布（箱子里黑球和白球的分布）。我们假设抽到黑球的概率为a，则抽到白球的概率为（1-a）。则抽到8次黑球，2次白球的似然函数为：L(a)=a8(1−a)2L(a)=a^8 (1−a) ^2L(a)=a8(1−a)2，注意这里抽到黑球的概率a为变量。a作为自变量，抽到8次黑球，2次白球事件的概率作为因变量。上式中的函数L(a)就是似然函数，我们可以绘制出这个函数的曲线：

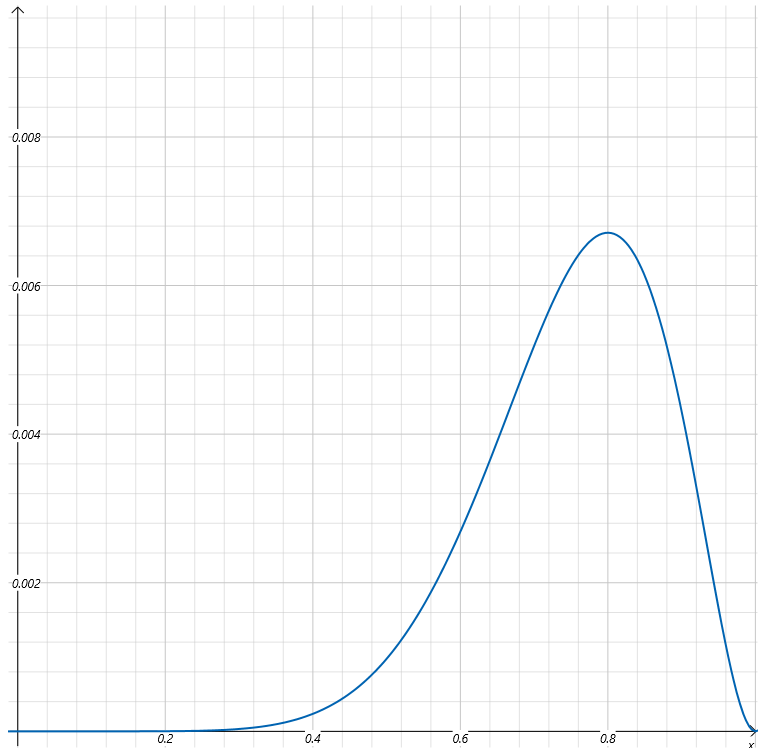
因为a为概率，它的取值只能在0到1之间。所以上图我们只取了a在0到1之间似然函数的图像。上边我们列出了连续抽了10次，8次是黑球，2次是白球这个事件的似然函数，这个事件已经发生了，似然函数表达了不同的分布参数让这个事件发生的可能性。自然我们会想到，最有可能的参数必然是让事件发生可能性最大的那个参数。通过观察上图，我们可以看到当a取0.8时，似然函数取最大值。也就是说，基于观察结果，箱子里的球有80%是黑球，是最有可能让事件发生的。

现在我们对上式取对数得到：ln(L(a))=ln(a8(1−a)2)=8lna+2ln(1−a)ln(L(a)) = ln(a^8 (1-a)^2) = 8lna + 2ln(1-a)ln(L(a))=ln(a8(1−a)2)=8lna+2ln(1−a)。图像为：

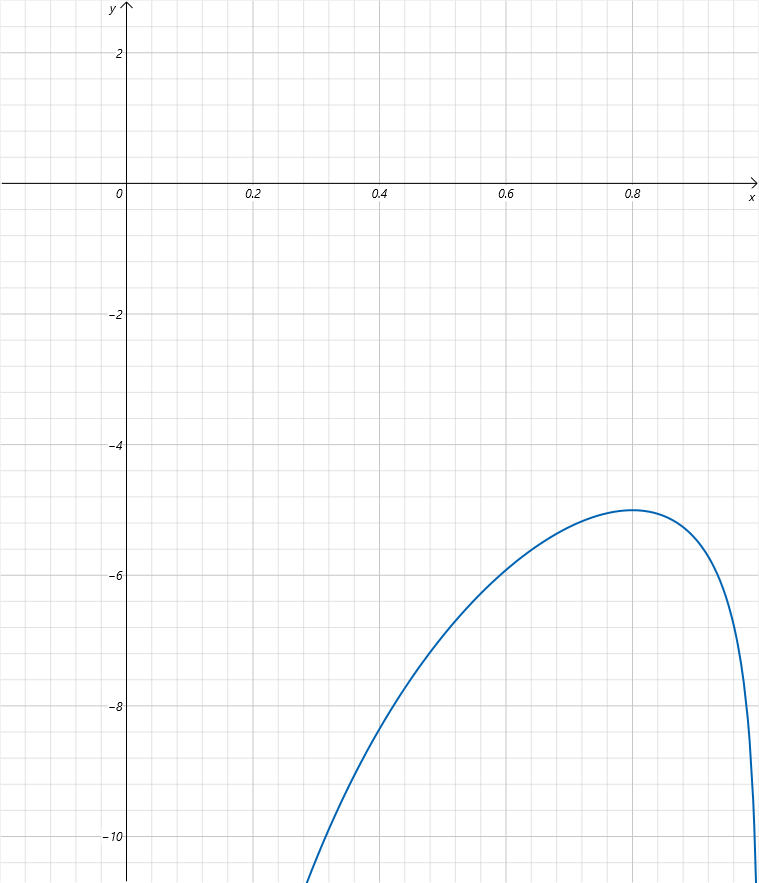
我们可以发现对原来的似然函数取对数，对数似然函数取得极值时的自变量并没有改变，还是0.8。

4、分类问题的模型评估指标

4.1 混淆矩阵

混淆矩阵是模型预测结果与实际标签的对比情况。

混淆矩阵的四个指标：

真实值是 正例 的样本中，被分类为 正例 的样本数量有多少，叫做真正例（TP，True Positive）

真实值是 正例 的样本中，被分类为 假例 的样本数量有多少，叫做伪反例（FN，False Negative）

真实值是 假例 的样本中，被分类为 正例 的样本数量有多少，叫做伪正例（FP，False Positive）

真实值是 假例 的样本中，被分类为 假例 的样本数量有多少，叫做真反例（TN，True Negative）

4.2 精确率

也叫查准率，对正例样本的预测准确率。计算方法为：

4.3 召回率

也叫查全率，指的是预测为真正例样本占所有真实正例样本的比重。计算方法：

4.4 F1 Score

综合精确率、召回率的指标。计算公式：

4.5 ROC曲线、AUC指标

真正率TPR与假正率FPR：

1 正样本中被预测为正样本的概率TPR （True Positive Rate）

2 负样本中被预测为正样本的概率FPR （False Positive Rate）

4.6 准确率

准确率就是模型预测正确的样本数占总样本数的比例。计算公式为：

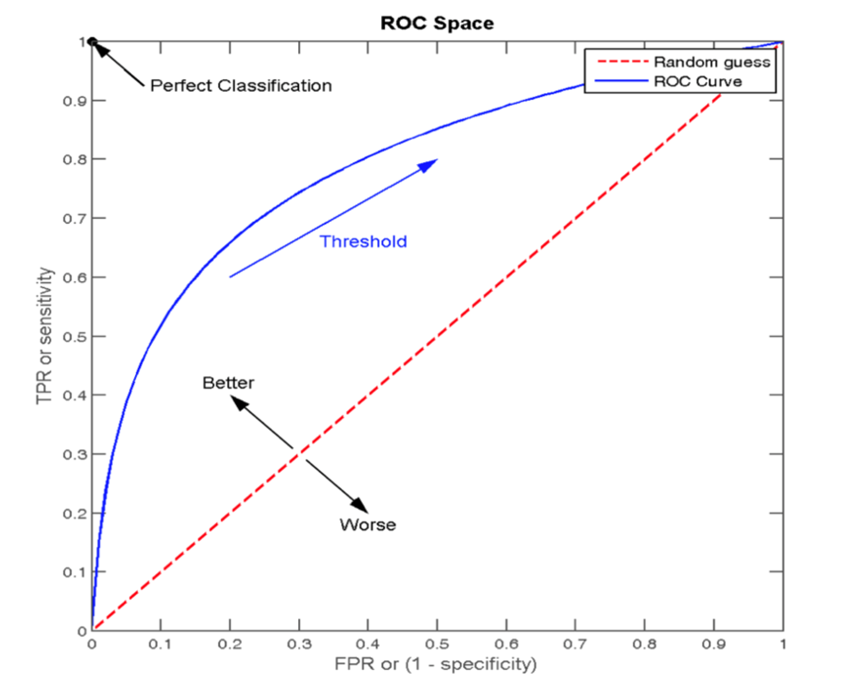
ROC曲线以模型的真正率TPR为纵轴，假正率FPR为横轴，它将模型在不同阈值下的表现以曲线的形式展现出来。曲线越靠近 (0,1) 点则模型对正负样本的辨别能力就越强。ROC曲线的优劣可以通过曲线下的面积（AUC）来衡量，AUC越大表示分类器性能越好。

5、API运用

5.1 API

逻辑回归API：

sklearn.linear_model.LogisticRegression(solver='liblinear', penalty='l2', C = 1.0)

参数：

solver 损失函数优化方法:
          1 liblinear 对小数据集场景训练速度更快，sag 和 saga 对大数据集更快一些。
          2 正则化：
	           1 sag、saga 支持 L2 正则化或者没有正则化
	           2 liblinear 和 saga 支持 L1 正则化
penalty：正则化的种类，l1 或者 l2
C：正则化力度 

查看混淆矩阵API：

sklearn.metrics.confusion_matrix()

分数API：

from sklearn.metrics import ***
accuracy_score() # 准确率
precision_score()	# 精确率
recall_score()	# 召回率
f1_score()	# F1分数
roc_auc_score(y_true, y_score)	# ROC、AUC
sklearn.metrics.classification_report(y_true, y_pred, labels=[], target_names=None )	# 分类评估报告

5.2 案例

电信客户流失案例：

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, roc_auc_score, confusion_matrix, classification_report

data = pd.read_csv('data/churn.csv')
print(data.head())
data_new = pd.get_dummies(data,drop_first=True)

print(data_new.head())
print(data_new.columns.values)
Featrues = data_new[['Partner_att','Dependents_att','landline','internet_att',
                     'StreamingTV','Contract_Month','Contract_1YR',
                     'PaymentElectronic','MonthlyCharges']]

labels = data_new['Churn_Yes']
x_train, x_test, y_train, y_test = train_test_split(Featrues, labels, test_size=0.2, random_state=6, stratify=labels)

ssm = StandardScaler()
ssm.fit_transform(x_train)
ssm.transform(x_test)

lrm = LogisticRegression(solver='liblinear',penalty='l2', tol=1e-4, C=1.0, fit_intercept=True)
lrm = GridSearchCV(lrm, param_grid={'C': np.arange(0.1, 1, 0.1)}, cv=6)
lrm.fit(x_train, y_train)
prediction = lrm.predict(x_test)

# 逻辑回归模型评估
print("准确率：", accuracy_score(y_test, prediction))
print("精确率：", precision_score(y_test, prediction))
print("召回率：", recall_score(y_test, prediction))
print("F1:", f1_score(y_test, prediction))
print("混淆矩阵", confusion_matrix(y_test, prediction, labels=[True, False]))
print("ROC---AUC值：", roc_auc_score(y_test, prediction))
print(classification_report(y_test, prediction))