【LeetCode】392.判断子序列

文章目录

【题目链接】
【题目描述】
【解题思路】

【题目链接】

392.判断子序列

【题目描述】

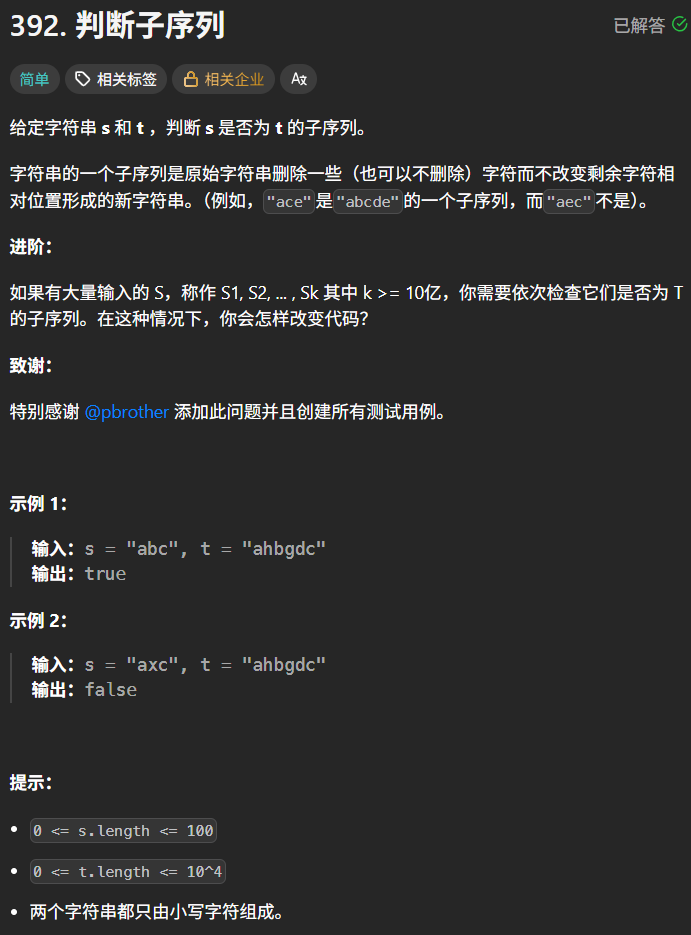
【解题思路】

本题采用双指针法是最优解，核心思路是通过两个指针分别遍历 s 和 t，逐步匹配 s 中的字符，利用 "子序列只需保持相对顺序" 的特性，高效判断匹配结果。

具体逻辑如下：

初始化指针：定义两个指针 i 和 j，分别指向 s 的起始位置（i=0）和 t 的起始位置（j=0）。
双指针遍历：
同时遍历两个字符串，只要 i 未遍历完 s（i < s.size()）且 j 未遍历完 t（j < t.size()），就持续循环。
若当前 s[i] 与 t[j] 相等，说明匹配成功，将 i 向后移动一位（继续匹配 s 的下一个字符）。
无论是否匹配成功，j 都需向后移动一位（继续遍历 t 的下一个字符，寻找可能匹配的字符）。
判断结果：遍历结束后，若 i 等于 s 的长度（i == s.size()），说明 s 中所有字符都在 t 中按顺序匹配成功，返回 true；否则返回 false。

C++ 实现：

cpp 复制代码

class Solution {
public:
    bool isSubsequence(string s, string t) {
        int n = s.size();
        int m = t.size();

        int i=0; 
        int j=0;

        while(i<n && j<m){
            if (s[i] == t[j]){
                i++;
            }
            j++;
        }

        return i==n;
    }
};

Python实现：

python 复制代码

class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
        
        m = len(s)
        n = len(t)

        i = 0
        j = 0 

        while i<m and j<n:
            if s[i] == t[j]:
                i+=1

            j+=1

        return i==m

时间复杂度：

算法的时间复杂度描述的是最坏情况下的执行效率。对于本题：
最坏情况是 s 不是 t 的子序列，且需要遍历完整个 t 才能确认（如上述例子），此时操作次数为 m。
因此，时间复杂度由 t 的长度 m 主导，即 O (m)，而非由 s 的长度 n 主导的 O (n)。

空间复杂度： O（1）