目录
[Adjacent XOR](#Adjacent XOR)
[Arboris Contractio](#Arboris Contractio)
引言:
本来今天也是打算讲一道题的,但是因为第一道的1400的题感觉有点过于简单了,感觉没有1400的题的感觉,于是就决定这篇讲俩题,而且好巧不巧,这俩题竟然是在同一场div3里的,而且更神奇的是,E题开出来的人竟然比D题还多,如图

但确实,我打下来也感觉D题比E题难打一点,那么接下来,我们就开始进行题目的讲解------------>

Adjacent XOR
那么,我们先来讲相对另一道而言总体偏简单的题目,我们先来分析一下题目
题意分析
这是题目链接Problem - 2131E - Codeforces
不想跳转可看下图

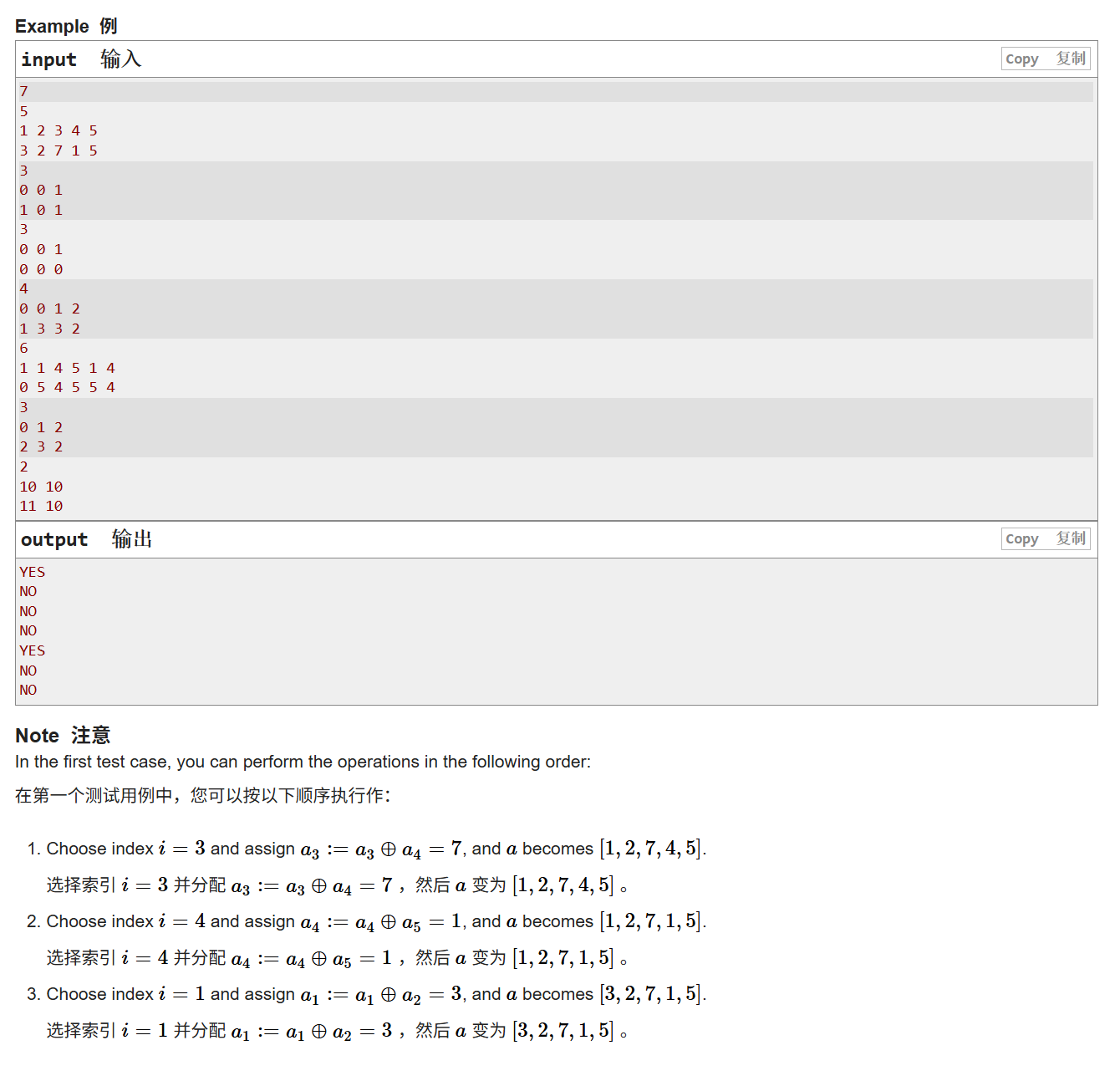
首先,我们来看题目,这个题目的描述十分的简单,就是给你一个数组a,然后问你能不能把这个数组a变成数组b
然后操作也很简单,就是可以随便选择下标(需要没被选择过的),然后对该下标和相邻的下一个下标的俩个值进行异或
题目的意思就这么简单,那么我们来将题目的要求进行逻辑梳理一番
逻辑梳理
首先,题目问我们a能不能转换成b,最简单的一个判断方式就是判断这俩个数组的最末尾元素是否一样,若不一样,则输出"NO",若一样,再进行讨论,为什么呢,我们来结合我画的图进行分析
根据题意,a数组的变化,撑死只能将最末尾的i与i+1进行变化,但这样变化后得到的新元素的位置也在i位,但是这种已经是最靠后的变化方式了,所以,我们可知,a数组的最后一位,是无法变化的,所以如果a跟b数组的末尾元素不一样,那么,a就不能转换为b
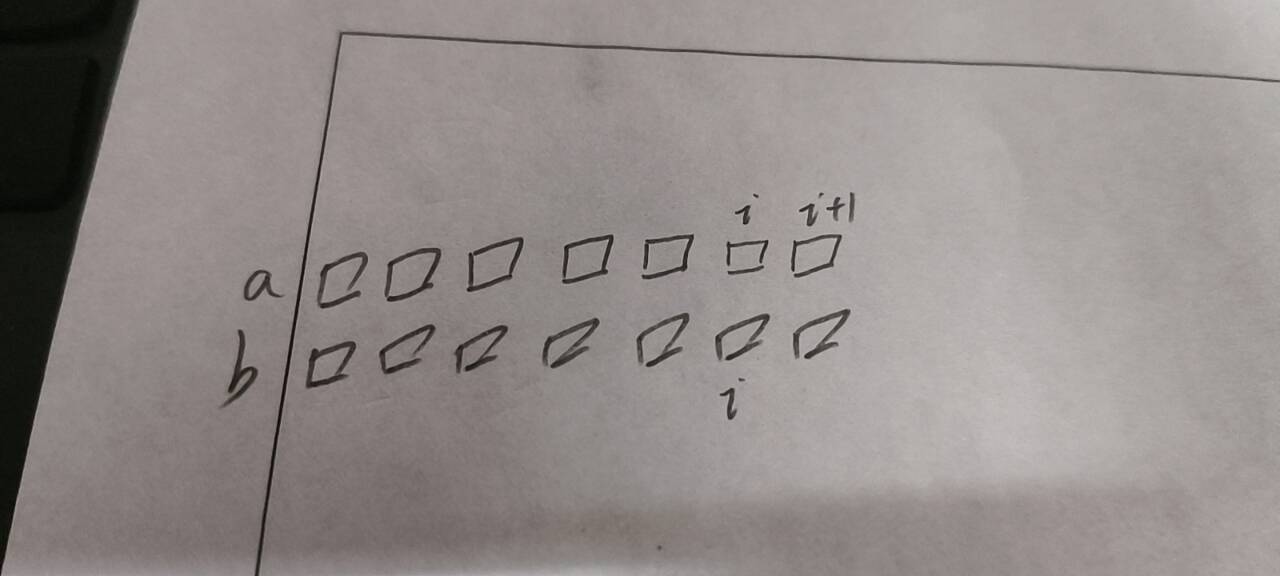
那么若a与b数组的末尾元素是一样的,接下来,我们来进行下一步的分析
首先,如果我们判断能否将a[i]变化成b[i],我们可以有俩种方式,一种是a[i]与b[i]是否一样,另一种是a[i]异或a[i+1]后是否与b[i]一样,不管是哪种情况,i 位置的能否转换都不会被 i 前面a数组的元素所影响,所以我们可以思考倒推,因为只有后面的元素可以对a[i]产生影响
因为题目告诉了我们,选择异或的顺序是可以任意的,所以当选择 i 这个位置进行判断时,会有三种情况
1.a[i]是否等于b[i]
2.a[i]^a[i+1]是否等于b[i]
3.a[i]^b[i+1]是否等于b[i]
只有这三个条件都无法满足时,才会输出"NO",那么我们具体来讲解下这三种情况
第一种情况很简单,相等的话不用操作就是符合的,很简单
第二种情况也很简单,就是 i+1 下标上的元素并没有选择进行异或,先对下标为 i 的位置进行异或,若等于,就可以变化(因为 i 在 i+1 前,所以 i+1 之后想要变化时候也不会被 i 的变化所影响)
第三种情况也好想,b[i+1]表示的是a[i+1]已经被进行异或过了,然后通过i与已经被异或过的i+1进行异或,若可以变化,则可以实现目的
所以,只有这三种情况都不满足时,才会使a数组无法变成b数组
那么,这个题目的思路已经理清楚了,那么代码也自然就很简单了,那么接下来,我们来写代码
代码实现
这个题主要是逻辑难想,逻辑想通了代码其实很简单,那么,这边就直接放AC的代码了
cpp
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <queue>
using namespace std;
int t, n;
long long a[200010];
long long b[200010];
int main()
{
cin >> t;
while (t--)
{
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
for (int i = 1; i<=n; i++)
cin >> b[i];
if (a[n] != b[n])
{
cout << "No" << endl;
continue;
}
int xixi = 1;
int j = n - 1;
while (j)
{
if (a[j] != b[j] && b[j] != (a[j] ^ b[j + 1]) && b[j] != (a[j] ^ a[j + 1]))
{
xixi = 0;
cout << "No" << endl;
break;
}
j--;
}
if (xixi)
cout << "Yes" << endl;
}
return 0;
}那么,这题就讲到这里结束啦,希望你们有所收获
接下来,我们来讲下一道题,下一道题跟上一道题刚好相反,思路好想,但是代码比较难实现
Arboris Contractio
那么,我们先来分析一下题目
题意分析
这是题目链接Problem - 2131D - Codeforces
不想跳转可看下图


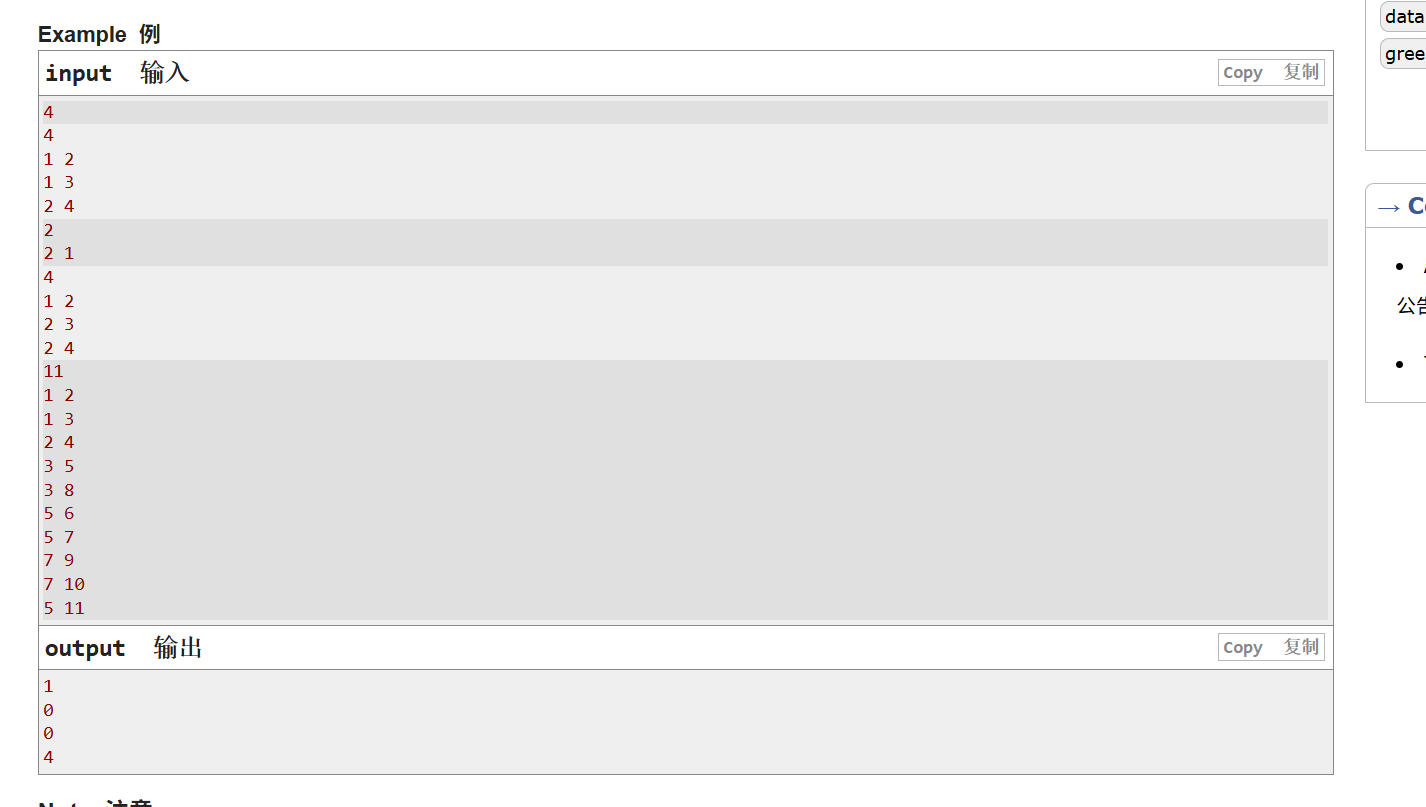
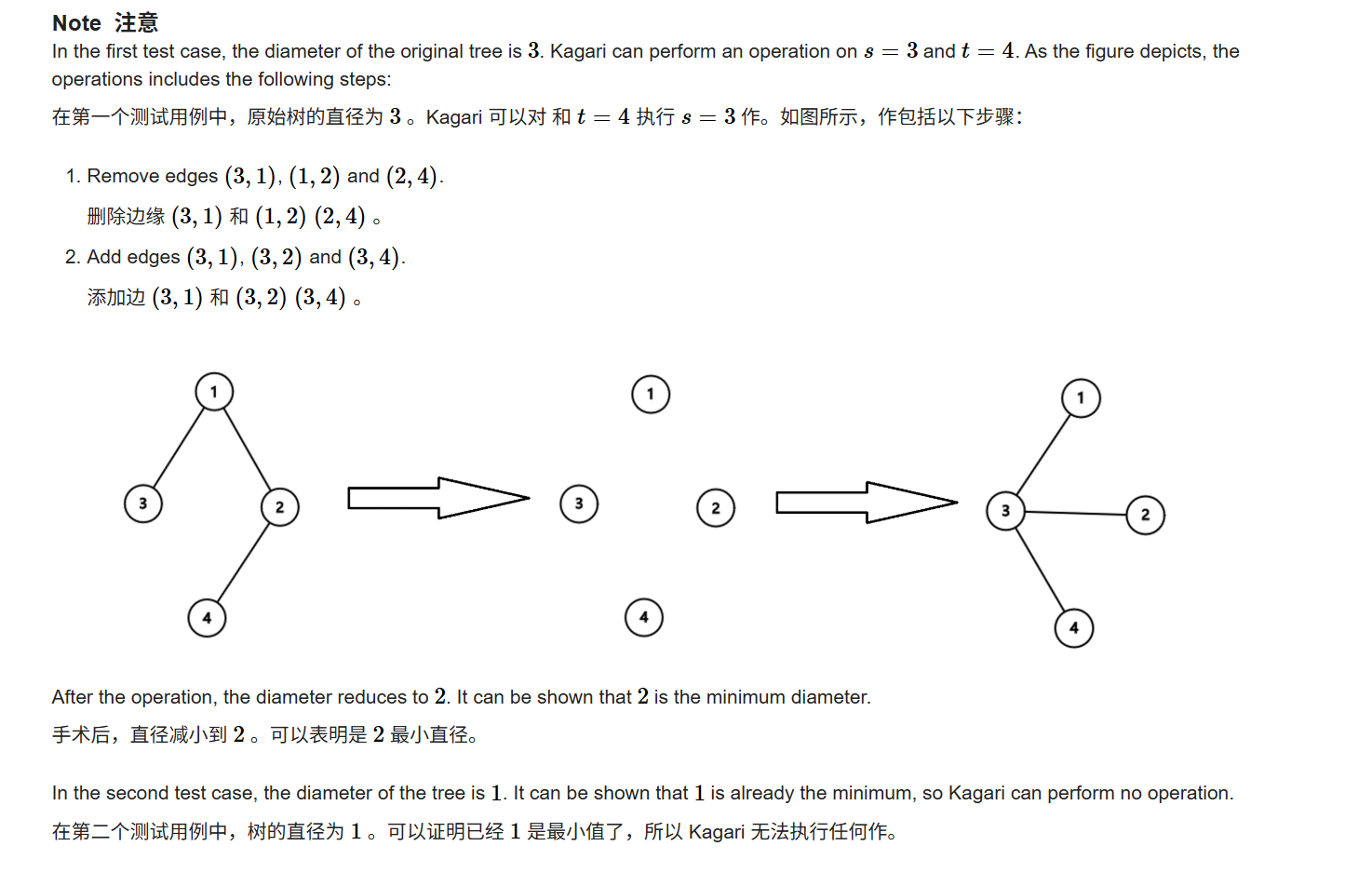
这题目相比上一题看着挺长的,但其实问的也很简单,就是题目会给你一个无环数,然后通过一系列的方法,将那颗无环树的深度变为2,然后问你最少的操作次数是几次,就没了
然后一次操作分为三步走,就是选一条路,然后把那条路所有的点全部拆开,然后再将后面的点全部跟头的那个点连上,就是一次操作
那么接下来,我们进行逻辑分析
逻辑梳理
逻辑其实很好梳理,首先,对于每个点的最少操作次数只需要数该节点深度不为1的分支有几条,分支的结果就是他需要操作的最小次数(这个自己理会,应该是很好理解的),然后通过一个个的对比,找出操作次数最少的一个节点,然后输出即可
思路是很清晰的,但是明显,这个思路是完全不可能实现的,因为若要实现这个思路,首先每个节点都要访问一遍,每次访问不同节点的时候,其他节点对于该节点的深度也会发生变化,而且每个节点的分支也不同,极多的不可控因素会使得这个思路完全无法转换成代码来实现,这也是困住了我挺久的地方
所以我们需要通过原先的思路,来创造出一个能转换成代码的思路
那么,既然是分支,我们就可以思考到叶子节点,因为每个点的分支,肯定最后都会抵达叶子节点,所以我们可以先算出这颗树总共有多少个叶子结点,然后一个循环,遍历完所有的点,每次遍历一个点的时候,可以将叶子节点的总数减去该节点已经有的深度为1的叶子节点的个数,这样得到的值便是该点的最少操作次数,这么一来,是不是就比一开始的时候的方式便捷了许多
注:我们可以进行特判,即若只有俩个点,那输出便为0,因为2个点不管怎么连都已经是最小宽度了,根本不需要进行任何操作
那么,逻辑梳理就梳理完了,接下来就进入代码实现部分
代码实现
在讲代码实现之前,特别注意,一定要把数组提到外面去,不然会导致栈溢出,切记,这点卡了我好久,结果发现原来是数组开在局部把栈区挤爆了(因为我一开始把数组放局部了,导致一运行就异常)那么,数组放在全局了,就不要忘了每次循环完进行清空操作
除开这点,别的就很简单了,我们用vector来存储每个点所相连接的点,然后通过判断点的size来确定该点是不是叶子结点,因为叶子节点的size肯定为1
然后我们想让总次数最少,只需要点的叶子结点最多即可,因为一个点的叶子节点越多,减去的值就越大,故而总次数越少
那么,接下来,我们就来看AC代码
cpp
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <queue>
#include <vector>
using namespace std;
int t, n;
vector<int> arr[200010];
void solv()
{
int u, v;
cin >> n;
for (int i = 1; i < n; i++)
{
cin >> u >> v;
arr[u].push_back(v);
arr[v].push_back(u);
}
if (n == 2)
{
cout << "0" << endl;
return;
}
int yesum = 0;
for (int i = 1; i <= n; i++)
if (arr[i].size() == 1)
yesum++;
int ye = 0;
for (int i = 1; i <= n; i++)
{
int Ye = 0;
for (int j = 0; j < arr[i].size(); j++)
{
if (arr[arr[i][j]].size() == 1)
Ye++;
}
ye = max(ye, Ye);
}
cout << yesum - ye << endl;
for (int i = 1; i <= n; i++)
{
while (arr[i].size())
arr[i].clear();
}
}
int main()
{
cin >> t;
while (t--)
{
solv();
}
return 0;
}那么,这题也讲完啦
结语:
今日算法讲解到此结束啦,希望对你们有所帮助,谢谢观看,如果觉得不错可以分享给朋友哟
