PCL法向量估计 之 RANSAC 平面估计法向量

1.点云中估计主平面法向量

2. 平面数学模型（PCL SACMODEL_PLANE）

任意三点 p1,p2,p3​ 构成平面：

（只要不共线）

平面法向量由叉乘获得

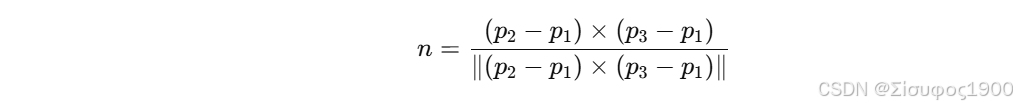
偏置项 d

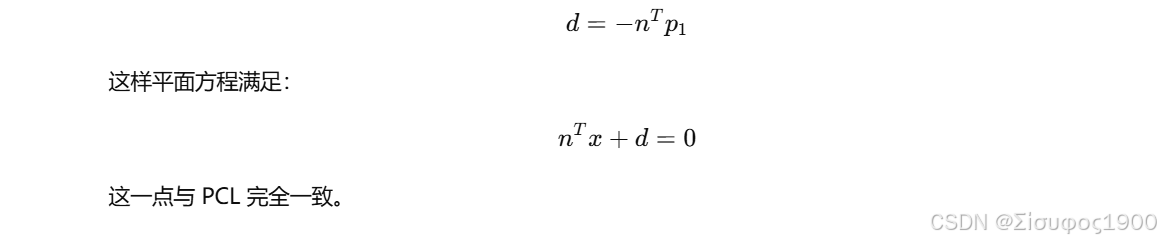
3. RANSAC 平面估计数学推导

RANSAC 过程：

---

Step 1：随机选 3 个点

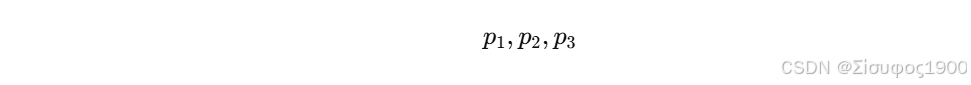
Step 2：计算平面

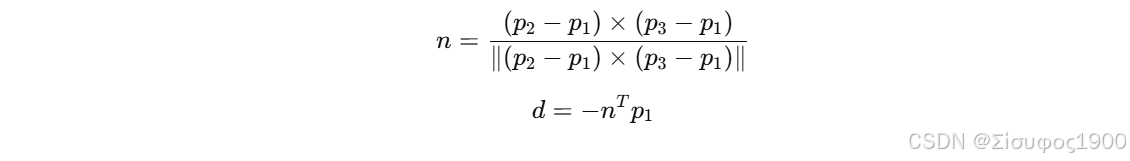
Step 3：计算每个点到平面的距离

Step 4：判断 inlier

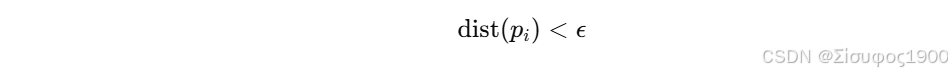
Step 5：选择 inlier 最多的平面

RANSAC 目标函数：

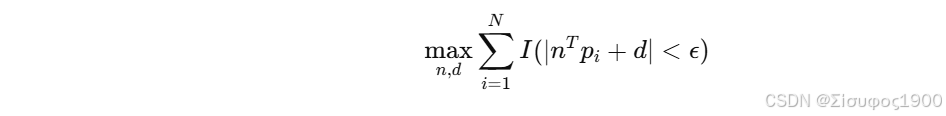
RANSAC 的问题

RANSAC 得到的是"粗糙"平面，只保证 inliers 多。

最终法向量并不是最精确

4. 最终精修：PCA 最小二乘平面拟合

PCL 在 segmentation 之后内部会执行：

优化后的法向量 = 最小特征向量

5、MATLAB 完整代码

%% PCL-Style RANSAC Plane Normal Estimation + Visualization
clc; clear; close all;

%% Load point cloud (replace with your bunny)
% pc = pcread('bun000.ply');
% Q = pc.Location;

% example: random plane + noise
N = 1000;
Q = rand(N,3);
Q(:,3) = 0.3*Q(:,1) + 0.6*Q(:,2) + 0.01*randn(N,1);

%% RANSAC parameters
maxIter = 200;
threshold = 0.01;
bestInliers = [];

%% RANSAC loop
for iter = 1:maxIter

    % 1. random 3 points
    idx = randperm(size(Q,1),3);
    p1 = Q(idx(1),:);
    p2 = Q(idx(2),:);
    p3 = Q(idx(3),:);

    % 2. plane normal
    n = cross(p2 - p1, p3 - p1);
    if norm(n) < 1e-6
        continue;
    end
    n = n / norm(n);

    % 3. d
    d = -dot(n,p1);

    % 4. distances
    dist = abs(Q * n' + d);

    % 5. inliers
    inliers = find(dist < threshold);
    if length(inliers) > length(bestInliers)
        bestInliers = inliers;
    end
end

fprintf("RANSAC inliers = %d\n", length(bestInliers));

%% Final PCA refinement
P = Q(bestInliers,:);

c = mean(P,1);
Xc = P - c;
C = Xc' * Xc;

[V,D] = eig(C);
[~,minIdx] = min(diag(D));
n_final = V(:,minIdx);
d_final = -dot(n_final,c);

fprintf("Final plane normal: [%.4f %.4f %.4f]\n", n_final);

%% Visualization
figure; hold on; axis equal;
scatter3(Q(:,1),Q(:,2),Q(:,3),5,'b');
scatter3(P(:,1),P(:,2),P(:,3),10,'r','filled');

% draw final normal
quiver3(c(1),c(2),c(3), n_final(1),n_final(2),n_final(3), ...
    0.2,'k','LineWidth',3);

legend('All Points','RANSAC Inliers','Plane Normal');
title('PCL-Style RANSAC Plane Normal Estimation');
xlabel X; ylabel Y; zlabel Z;
grid on;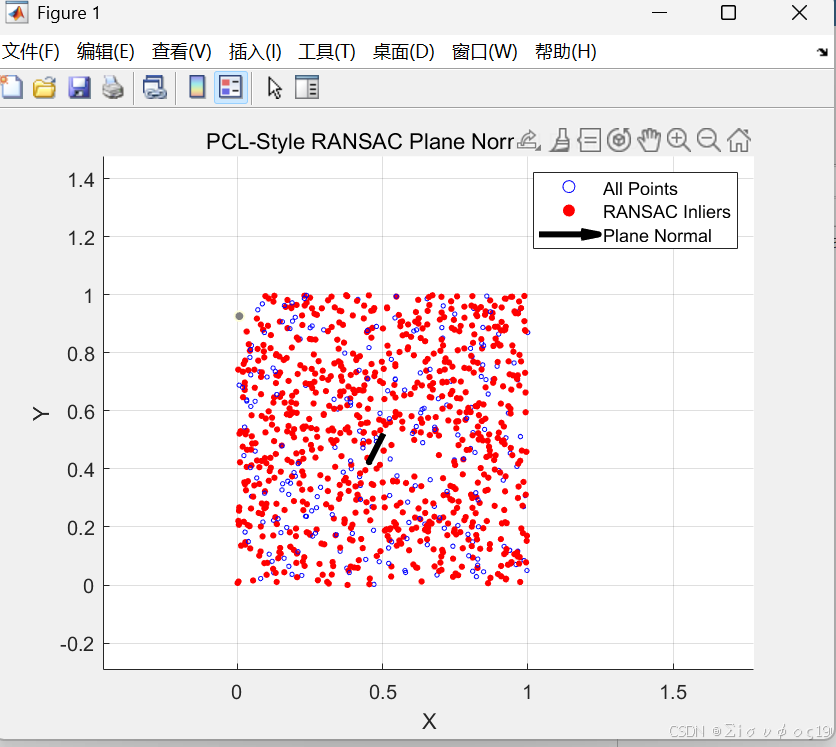

6、PCL 的一一对应关系

MATLAB 步骤	PCL C++ 对应函数
随机采样 3 点	SampleConsensusModelPlane::computeModelCoefficients
点到平面距离	selectWithinDistance
选择 inliers 最多	SACSegmentation::segment
最终 PCA 平面拟合	optimizeModelCoefficients