1 今日打卡
组合总和Ⅱ 40. 组合总和 II - 力扣(LeetCode)
分割回文串 131. 分割回文串 - 力扣(LeetCode)
2 组合总和
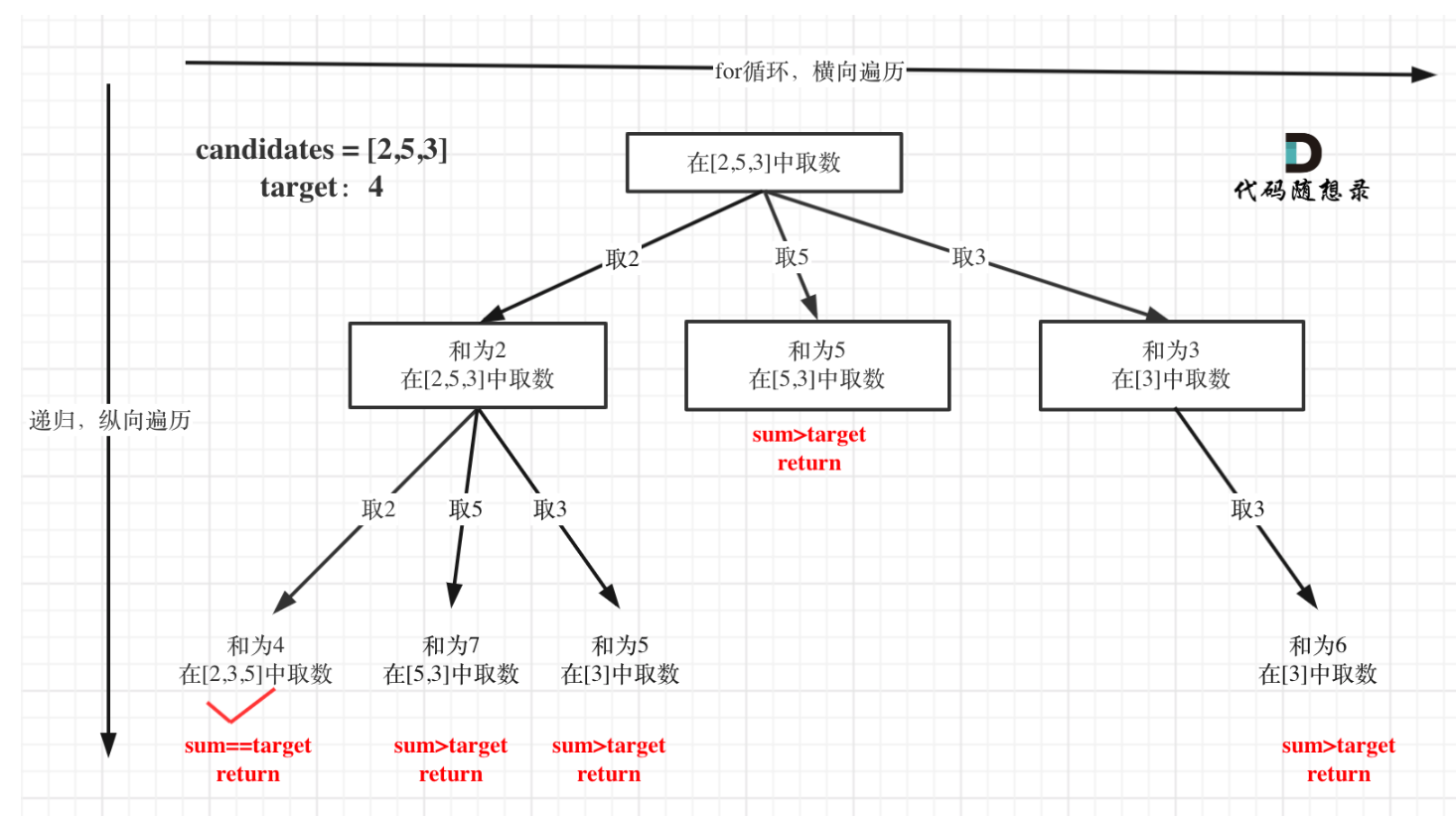
2.1 思路
剪枝:sum > target 时直接返回,减少无效递归,提升效率。
终止条件:sum == target 时,必须创建 path 的新副本存入 res(因为 path 是全局变量,后续回溯会修改它)。
循环与递归:
startIndex:确保组合不重复(比如选了 2 之后,只从 2 及之后的元素选,避免出现 [2,3] 和 [3,2] 这种重复组合)。
递归时传入 i 而非 i+1:允许重复选取当前元素(比如 candidates=[2,3,6,7],target=7 时,能选 [2,2,3])。
回溯:递归返回后,撤销当前选择(移除元素、恢复 sum),继续尝试下一个元素。
2.2 实现代码
java
class Solution {
// 全局变量:存储当前正在构建的单个组合(路径),如[2,2]
List<Integer> path = new ArrayList<>();
// 全局变量:存储最终所有符合条件的组合(结果集),如[[2,2,3],[7]]
List<List<Integer>> res = new ArrayList<>();
// 全局变量:实时记录当前path中元素的和,避免每次遍历path求和,提升效率
int sum = 0;
/**
* 主方法:对外暴露的入口,调用回溯函数并返回最终结果
* @param candidates 无重复元素的候选数字数组
* @param target 目标和
* @return 所有和为target的组合列表
*/
public List<List<Integer>> combinationSum(int[] candidates, int target) {
// 调用回溯核心函数,起始索引为0(控制组合不重复的关键)
backtracking(candidates, target, 0);
return res;
}
/**
* 回溯核心函数:递归遍历所有可能的组合,实现"选择-递归-回溯"的核心逻辑
* @param candidates 候选数字数组
* @param target 目标和
* @param startIndex 遍历起始索引(避免组合重复,如[2,3]和[3,2])
*/
public void backtracking(int[] candidates, int target, int startIndex) {
// 剪枝条件:当前路径和超过目标值,无需继续递归,直接返回(减少无效递归)
if (sum > target) {
return;
}
// 终止条件:当前路径和等于目标值,找到有效组合
if (sum == target) {
// 必须创建path的副本存入res!因为path是全局变量,后续回溯会修改它
res.add(new ArrayList<>(path));
return; // 找到结果后返回上一层递归,继续寻找其他组合
}
// 单层递归逻辑:横向遍历当前层的所有可选数字
// i从startIndex开始,保证组合不重复(只向后选,不回头选)
for (int i = startIndex; i < candidates.length; i++) {
// 1. 选择当前元素:将数字加入路径,更新当前和
path.add(candidates[i]);
sum += candidates[i];
// 2. 递归深入:继续选择下一个数字(传i而非i+1,允许重复选取当前元素)
backtracking(candidates, target, i);
// 3. 回溯撤销:移除最后一个元素,恢复sum,准备尝试下一个数字
sum -= candidates[i];
path.remove(path.size() - 1); // 栈式移除,只删最后一个元素
}
}3 组合总和Ⅱ
3.1 思路
排序的作用:
让重复元素相邻,为 "同一层跳过重复元素" 的去重逻辑铺路;
让数组有序,可在循环中通过 sum + candidates[i] > target 提前终止循环(剪枝)。
终止条件和剪枝:
sum > target:剪枝条件,提前终止无效递归(比如 sum=8、target=7 时,直接返回);
sum == target:终止条件,找到符合条件的组合,必须创建 path 的新副本存入 res(因为 path 是全局变量,后续回溯会修改它)。
去重逻辑:
去重优化:排序后,同一层递归中跳过重复元素(i > startIndex && candidates[i]==candidates[i-1]),避免结果出现重复组合;
3.2 实现代码
java
class Solution {
// 存储当前正在构建的单个组合(路径)
List<Integer> path = new ArrayList<>();
// 存储最终所有符合条件的组合(结果集)
List<List<Integer>> res = new ArrayList<>();
// 实时记录当前path中元素的和(优化效率,避免重复求和)
int sum = 0;
/**
* 主方法:对外暴露的入口,处理排序并调用回溯函数
* @param candidates 包含重复元素的候选数组
* @param target 目标和
* @return 所有符合条件的组合列表
*/
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
// 排序:1.让重复元素相邻(为去重铺路);2.支持提前剪枝
Arrays.sort(candidates);
// 调用回溯函数,起始索引为0(控制遍历起点,避免组合顺序重复)
backtracking(candidates, target, 0);
return res;
}
/**
* 回溯核心函数:递归遍历所有可能的组合,实现"选-递归-回溯"逻辑
* @param candidates 候选数组(已排序)
* @param target 目标和
* @param startIndex 遍历起始索引(控制组合不重复,且元素仅用一次)
*/
public void backtracking(int[] candidates, int target, int startIndex) {
// 剪枝条件:当前和超过目标值,无需继续递归,直接返回
if (sum > target) {
return;
}
// 终止条件:找到和为target的有效组合
if (target == sum) {
// 必须创建path的副本存入res!否则回溯会修改res中的内容
res.add(new ArrayList<>(path));
return;
}
// 单层递归逻辑:横向遍历当前层的所有可选元素
for (int i = startIndex; i < candidates.length; i++) {
// 优化剪枝:排序后,当前元素+sum > target → 后续元素更大,直接终止循环
if (sum + candidates[i] > target) {
break;
}
// 去重核心逻辑:同一层递归中,跳过和前一个元素重复的元素
// i > startIndex:保证是"同一层"的重复元素(而非不同层)
if (i > startIndex && candidates[i] == candidates[i - 1]) {
continue;
}
// 1. 选择当前元素:加入路径,更新当前和
path.add(candidates[i]);
sum += candidates[i];
// 2. 递归深入:i+1 表示当前元素只能用一次(和combinationSum1的核心区别)
backtracking(candidates, target, i + 1);
// 3. 回溯撤销:移除最后一个元素,恢复sum,准备选下一个元素
sum -= candidates[i];
path.remove(path.size() - 1);
}
}4 分割回文串
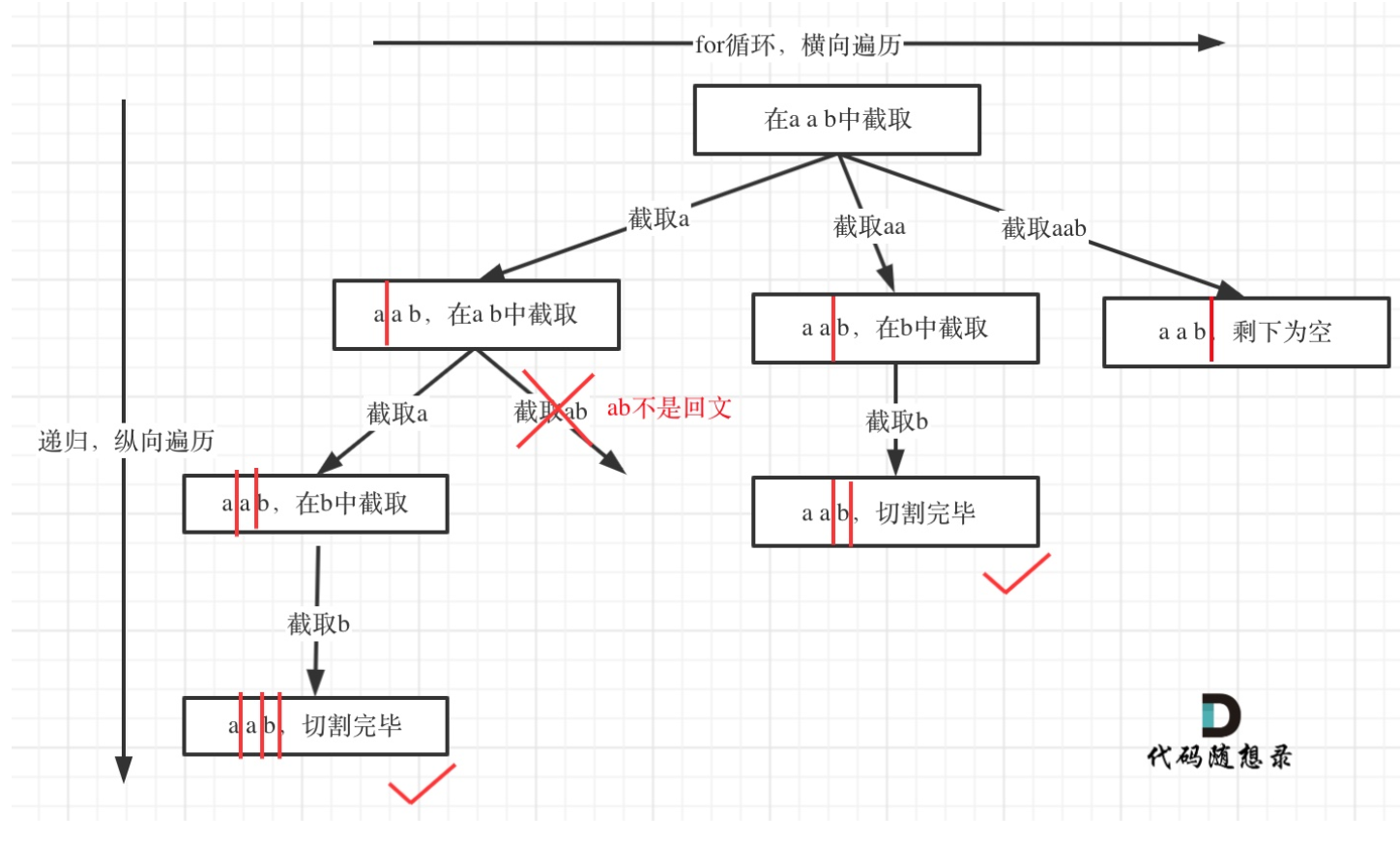
4.1 思路
循环变量 i:表示「当前切割的结束位置」,从 startIndex 开始遍历(比如 startIndex=0 时,i 依次取 0、1、2...,对应切割出 s[0]、s[0-1]、s[0-2]...);
isPalind(str, startIndex, i):判断 [startIndex, i] 区间的子串是否为回文(只有是回文才允许切割);
str.substring(startIndex, i + 1):截取 [startIndex, i] 区间的子串(因为 substring 是左闭右开,所以结束索引要 + 1);
递归传 i + 1:下一次切割从当前结束位置的下一个字符开始(保证子串不重叠、不遗漏);
回溯:递归返回后,移除 path 最后一个元素,回到切割前的状态,尝试下一个切割点。
4.2 实现代码
java
class Solution {
// 存储当前正在构建的分割方案(如["a","a"])
List<String> path = new ArrayList<>();
// 存储所有符合条件的分割方案
List<List<String>> res = new ArrayList<>();
/**
* 主方法:对外暴露的入口,调用回溯函数并返回结果
* @param s 待分割的字符串
* @return 所有符合条件的分割方案
*/
public List<List<String>> partition(String s) {
// 调用回溯函数,起始切割位置为0(从第一个字符开始)
backtracking(s, 0);
return res;
}
/**
* 回溯核心函数:递归切割字符串,寻找所有回文分割方案
* @param str 待分割的原字符串
* @param startIndex 下一次切割的起始位置(控制切割不重复、不遗漏)
*/
public void backtracking(String str, int startIndex) {
// 终止条件:切割完整个字符串(startIndex超出字符串长度)
if (startIndex >= str.length()) {
// 存入path的副本!避免回溯修改res中的内容
res.add(new ArrayList<>(path));
return;
}
// 单层递归逻辑:遍历所有可能的切割结束位置
// i表示当前切割的结束位置(从startIndex开始,到字符串末尾)
for (int i = startIndex; i < str.length(); i++) {
// 关键判断:[startIndex, i]区间的子串是否为回文
if (isPalind(str, startIndex, i)) {
// 是回文:截取该子串(substring左闭右开,所以结束索引+1)
String palindromeSub = str.substring(startIndex, i + 1);
// 将该回文子串加入当前分割方案
path.add(palindromeSub);
// 递归:下一次切割从i+1开始(当前子串已处理完,不重复切割)
backtracking(str, i + 1);
// 回溯:撤销本次切割,尝试下一个切割点
path.remove(path.size() - 1);
}
// 不是回文:直接跳过,不切割该区间
}
}
/**
* 辅助方法:双指针法判断指定区间的子串是否为回文
* @param str 原字符串
* @param left 子串左边界(包含)
* @param right 子串右边界(包含)
* @return true=是回文,false=不是回文
*/
public boolean isPalind(String str, int left, int right) {
// 双指针向中间靠拢,逐一比较字符
while (left <= right) {
// 字符不相等,直接返回false
if (str.charAt(left) != str.charAt(right)) {
return false;
}
left++; // 左指针右移
right--; // 右指针左移
}
// 所有字符都相等,是回文
return true;
}