【论文阅读】Towards Privacy-Enhanced and Robust Clustered Federated Learning

Towards Privacy-Enhanced and Robust Clustered Federated Learning -- 面向隐私增强和鲁棒聚类的联邦学习

论文来源

名称	Towards Privacy-Enhanced and Robust Clustered Federated Learning
期刊	TMC 2025
作者	Yang Xu , Yunlin Tan , Cheng Zhang , Peng Sun , Yibang Zhang , Ju Ren , Senior Member, IEEE, Hongbo Jiang , Senior Member, IEEE, and Yaoxue Zhang , Senior Member, IEEE
DOI	DOI: 10.1109/TMC.2025.3547149

问题背景

联邦学习（Federated Learning, FL）允许多个客户端在保护隐私的前提下协同训练模型，但传统的FL往往训练一个共享的全局模型。在实际场景中，客户端的数据分布通常存在非独立同分布（non-IID），这会导致全局模型性能显著下降。
现有CFL方法通常依赖客户端的梯度信息来衡量数据分布相似性并进行聚类。问题在于：
- 共享的梯度可能会被梯度反演攻击利用，重构出原始的训练数据（如像素级图像），造成严重隐私泄露。
- 常见的隐私保护机制（差分隐私、同态加密、安全聚合等）在聚类阶段并不奏效，因为它们要么引入噪声干扰聚类，要么只提供聚合后的梯度，无法支持精确的客户端聚类。
CFL除了继承FL中的常见攻击风险（如模型中毒攻击），还引入了新的安全威胁：
- 恶意集群攻击（malicious cluster attack）：一小部分恶意客户端可以通过伪造或构造相似的数据分布，集中到某些聚类中，占据多数并操纵该聚类的训练过程，从而破坏整体模型的鲁棒性。
- 现有检测方法要么计算开销过大（需在每轮训练检测上传模型），要么在面对恶意多数的聚类时无能为力。

TDLR

这篇论文针对聚类式联邦学习（CFL）中存在的隐私泄露风险（梯度反演攻击）和恶意客户端中毒攻击 问题展开研究。作者提出了一个名为 ProCFL 的框架，通过梯度无关的相似性度量与聚类 结合同伴验证机制，在提升隐私保护的同时增强了对攻击的抵御能力。实验结果表明，ProCFL在非IID和对抗场景下都能取得比现有方法更好的鲁棒性与模型性能。

系统架构

实体

本文的系统由三种实体构成：客户端、集群领导者、中央服务器。

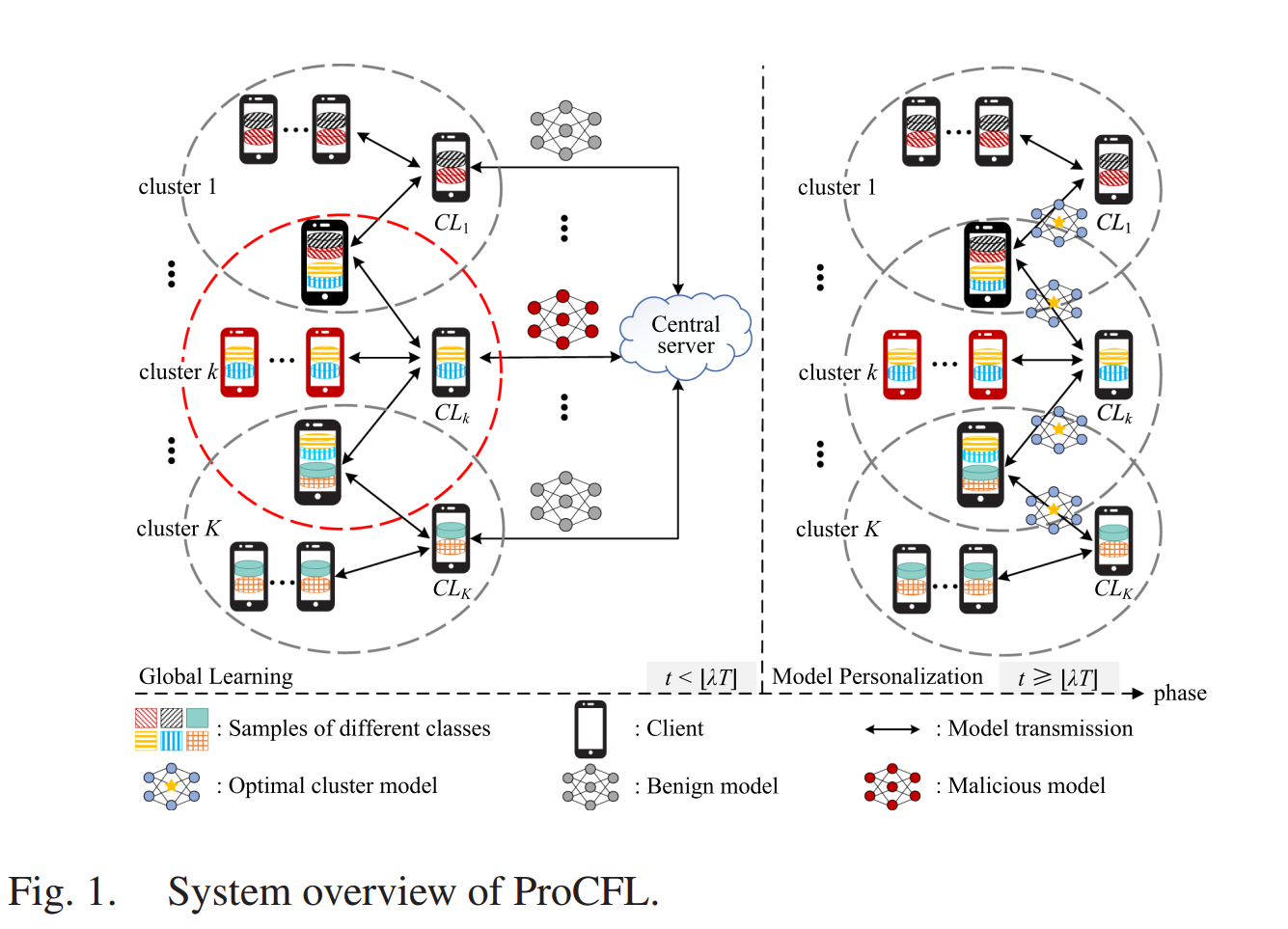
客户端：在CFL系统中存在一个由 N = { 1 , . . . , N } N = \{1, . . . , N\} N={1,...,N} 表示的客户端集合。每个客户端 n ∈ N n \in N n∈N 拥有一个私有数据集 D n D_n Dn，其统计特性在各个客户端之间并不相同。所有客户端根据其数据分布被聚类为 K K K 个组。同一聚类中的客户端协作训练一个个性化模型，以适配其数据分布。
集群领导者：假设 N N N 个客户端被组织成一个集群集合 K = { 1 , ... , K } K = \{1, ..., K\} K={1,...,K}，每个集群包含 n k n_k nk 个客户端。每个集群 k ∈ K k \in K k∈K 随机选择一个内部客户端作为集群领导者，记为 C L k CL_k CLk，负责聚合该集群内所有客户端的集群模型。
中央服务器：该服务器初始化全局模型并设置超参数。在训练过程中，服务器负责将客户端聚类为 k k k 个簇并聚合全局模型。

威胁模型

攻击者：本文考虑两类型的攻击：

由诚实但好奇的发起的数据重建攻击；
由恶意客户端（由对手攻陷的良性客户端）发的投毒攻击。

算法实现

联邦学习工作流

所有客户端首先共同训练全局模型，在此基础上，每个簇内的客户端再迭代训练个性化模型。具体而言，在初始化阶段，服务器初始化模型参数和超参数，并设定模型训练的总轮数 T T T、全局学习轮数 λ T ( λ ∈ [ 0 , 1 ] ) \lambda T (\lambda \in [0,1]) λT(λ∈[0,1])以及个性化训练轮数 ( 1 − λ ) T (1 −\lambda )T (1−λ)T。服务器还利用聚类算法对客户端进行聚类。在每一轮 ProCFL 中，依次执行以下步骤（见算法 1）：

一、本地训练

在每一轮全局学习 t ( t < λ T ) t( t < \lambda T ) t(t<λT)中，每个客户端 n ∈ N n \in N n∈N 首先将其本地数据集 D n D_n Dn 划分为大小为 B n B_n Bn 的小批量集合 B n B_n Bn。然后，客户端 n n n 执行本地模型更新，其中 E n E_n En 是客户端 n n n 的本地训练轮数。
w t , i = w t , i − 1 − η g ( w t , i − 1 ; b ) w^{t,i} = w^{t,i−1} − \eta g (w^{t,i−1}; b) wt,i=wt,i−1−ηg(wt,i−1;b)

在每一轮模型个性化阶段 t ( t ≥ λ T ) t(t \ge \lambda T) t(t≥λT)中，每个客户端 n ∈ N n \in N n∈N 都进行相同的本地训练。对于具有多种数据样本类别并被分到多个聚类中的客户端，他们将从不同的聚类领导者处接收多个聚类模型。在这些聚类模型中，客户端将选择在其本地数据上测试损失值最小的模型进行本地模型更新。形式化地，聚类索引 k k k 的确定方式如下：
k = a r g m i n k ∈ C n f ( w k t ; D n ) k = argmin_{ k \in \mathcal{C}_n} f (w_k^t; D_n ) k=argmink∈Cnf(wkt;Dn)

其中 C n C_n Cn 表示客户端 n n n 同时归入的簇集合， f ( w k t ; D n ) f (w_k^t; D_n) f(wkt;Dn) 表示簇模型 w k t w_k^t wkt 在客户端 n n n 的本地数据集 D n D_n Dn 上的测试损失函数。

二、集群领导者的集群聚合

在完成本地训练后，每个客户端将更新后的本地模型上传至其对应的集群领导者。当集群领导者 C L k ( ∀ k ∈ K ) CL_k (∀k \in \mathcal{K}) CLk(∀k∈K)接收到来自集群 k k k 所有客户端的本地模型后，执行集群聚合
w k t + 1 = 1 n k ∑ n = 1 n k w n t + 1 w_k^{t+1} = \frac{1}{n_k} \sum_{n=1}^{n_k} w_n^{t+1} wkt+1=nk1n=1∑nkwnt+1

其中 n k n_k nk 表示簇 k k k 中的客户端数量。

接下来，集群领导者 C L k CL_k CLk 要么将 w k t + 1 w_k^{t+1} wkt+1 发送回集群客户端进行下一轮本地训练（模型个性化阶段），要么将 w k t + 1 w_k^{t+1} wkt+1 上传至服务器进行全局模型聚合（全局聚合阶段）。

三、中央服务器全局聚合

在全局聚合阶段，服务器将在每一轮 t t t 接收聚类模型 w k t + 1 ( ∀ k ∈ K ) w_k^{t+1} (∀k \in \mathcal{K}) wkt+1(∀k∈K)，然后将其聚合以获得新的全局模型
w t + 1 = 1 K ∑ k = 1 K w k t + 1 w^{t+1} = \frac{1}{K} \sum_{k=1}^{K} w_k^{t+1} wt+1=K1k=1∑Kwkt+1

ProCFL技术细节

在本研究中提出了一个新颖的聚类框架，不仅实现无梯度聚来实现隐私增强的客户端聚类，还能有效抵御恶意攻击。ProCFL融合了三项核心，即数据分布相似性度量 、 多样性优化的客户端聚类 以及 恶意聚攻击检测 ，如图2所示。

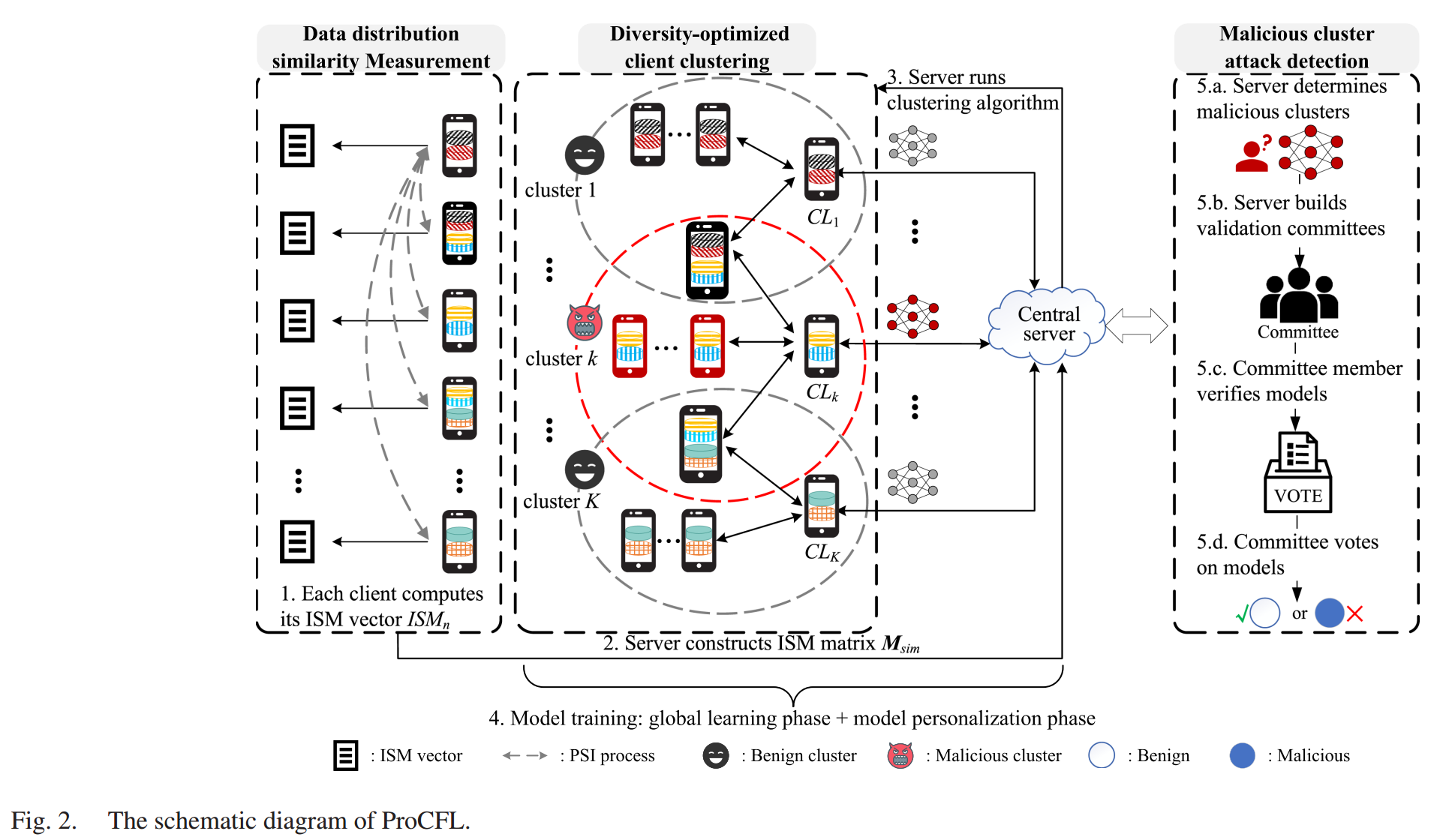
无梯度的分布相似性度量

现有的相似性度量方法通常基于客户端的原始梯度，这会为复杂的深度学习模型带来较大的计算开销。更为严重的是，直接使用原始梯度作为度量会带来严重的隐私风险（例如，梯度反演攻击）。

但是不是有好多直接使用数据分布相似度吗

此外，度量指标也不应泄露客户端的数据分布信息，因为这可能会暴露其诸如个人偏好等敏感信息。因此，那些具有对称性质的数据分布相似度量（例如，Jaccard 相似系数）是不合适的。如果使用对称度量来计算相似度，那么某个特定客户端就能够根据该相似度判断另一方的数据分布是否与其自身相似。

鉴于上述考虑，本文设计了ISM（intersection similarity metric，交集相似度度量）。为了形式化地描述ISM，首先为每个客户端构建一个与数据分布相关的集合，令 L = { 1 , ... , L } L = \{1, ..., L\} L={1,...,L} 表示数据集的可能标签集合。然后，每个客户端 n ∈ N n \in N n∈N 统计属于每个类别 l ∈ L l \in L l∈L 的数据样本数量 X n l X_n^l Xnl。将可能标签的集合及其对应的数据样本数量汇总为集合 Q n = { ( 1 , X n 1 ) , ... , ( l , X n l ) , ... , ( L , X n L ) } \mathcal{Q}n = \{(1, X_n^1), ..., (l, X_n^l), ..., (L, X_n^L)\} Qn={(1,Xn1),...,(l,Xnl),...,(L,XnL)} 。对于每一对 ( l , X n l ) (l, X_n^l) (l,Xnl)，我们构建一个集合如下：
Q n l = ∪ i = 1 X n l ( l × Q m a x + i ) Q_n^l= \cup{i=1}^{X_n^l} (l \times \mathcal{Q}_{max} + i) Qnl=∪i=1Xnl(l×Qmax+i)

因为 Q m a x \mathcal{Q}_{max} Qmax 设置的足够大，所以每个样本可以分配一个唯一的标识符。

然后，每个客户端 n n n 构建与数据分布相关的集合：
χ i = ∪ l = 1 L Q n l \chi_i=\cup_{l=1}^{L}\mathcal{Q}_n^l χi=∪l=1LQnl

定义 1 .（交集相似度度量）：对于每个客户端 n ∈ N n \in N n∈N，其相对于客户端 m m m 的 ISM 计算如下：
I S M n [ m ] = ∣ χ n ∩ χ m ∣ ∣ χ n ∣ ISM_n [m] =\frac{|\chi_n \cap \chi_m|}{|\chi_n|} ISMn[m]=∣χn∣∣χn∩χm∣

在此， I S M n [ m ] ∈ [ 0 , 1 ] ISM_{n}[m] ∈ [0, 1] ISMn[m]∈[0,1] 表示 χ n \chi_{n} χn 与 χ m \chi_{m} χm 之间共有元素数量占 χ n \chi_{n} χn 基数的比例。因此， I S M n [ m ] ISM_{n}[m] ISMn[m] 可用于表征客户端 n n n 与 m m m 之间数据分布的相似程度。并且，ISM 是一种非对称度量，因为 I S M n [ m ] = 1 ISM_{n}[m] = 1 ISMn[m]=1 仅表明两个相关客户端的数据分布相似，但不一定完全相同。

本文采用基于 Rivest--Shamir--Adleman（RSA）的 PSI 协议（RSA-PSI）在客户端之间以安全和私密的方式计算 ISM。客户端 n n n 将与其他客户端（包括其自身）的 ISM 值汇总为一个 ISM 向量
I S M n = ( ∣ χ ∩ χ 1 ∣ ∣ χ n ∣ , ∣ χ ∩ χ 2 ∣ ∣ χ n ∣ , . . . , ∣ χ ∩ χ N ∣ ∣ χ n ∣ ) = ( I S M n [ 1 ] , I S M n [ 2 ] , . . . , I S M n [ N ] ) ISM_n =\big( \frac{|\chi \cap \chi_1|}{|\chi_n|},\frac{|\chi \cap \chi_2|}{|\chi_n|},...,\frac{|\chi \cap \chi_N|}{|\chi_n|} \big)\\=(ISM_n[1],ISM_n[2],...,ISM_n[N]) ISMn=(∣χn∣∣χ∩χ1∣,∣χn∣∣χ∩χ2∣,...,∣χn∣∣χ∩χN∣)=(ISMn[1],ISMn[2],...,ISMn[N])

多样性优化的客户端聚类

为实现客户端聚类，服务器手机每个客户端 n ∈ N n \in N n∈N 的 ISM量 I S M n ISM_n ISMn ，并构建一个 ISM 矩阵 M s i m ∈ R N × N M_{sim} \in \mathbb{R}^{N \times N} Msim∈RN×N

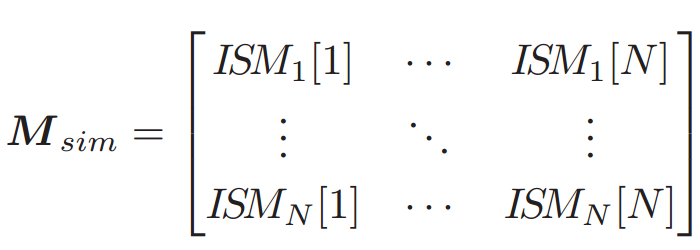
本文没有直接采用传统的聚类或匹配算法，主要有两个原因。

首先，传统的聚类技术通常将客户端分配到单一簇中，这限制了具有样化数据类别客户端为多个簇模型的训练做出贡献。这种限制削弱了它们降低簇模型之间差异的能力，从而最终影响全局模型的性能。
其次，尽管一些聚类方法旨在解决上述问题，但它们通常假设客户端之间的相似性是对称的，由我们的 ISM 指标捕获的数据分布相似性是非对称的使得这些方法不适用。

为了解决这些问题，本文提出了一种多样性优化的客户端聚类。具体而言，客户端聚类过程转化为基于 ISM 矩阵 M s i m M_{sim} Msim 的权重集合覆盖问题（weighted set covering problem，WSCP）。

权重集合覆盖问题简介：WSCP是一个数学优化问题，涉及在每个具有相关成本或权重的情况下，选择最少数量的集合，所选集合的并集能够覆盖给定的基础集合。

形式上，WSCP 定义如下。设 Ω \Omega Ω 为包含 m m m 个元素的集合 Ω = { 1 , ... , m } \Omega = \{1, ..., m\} Ω={1,...,m}，并设 S S S 为 Ω \Omega Ω 的 p p p 个子集的集合，即 S = { S 1 , ... S p } S = \{S_1, ... S_p\} S={S1,...Sp}，其中每个元素都是 Ω \Omega Ω 的一个子集。 S S S 中的每个子集都有一个相关的成本或权重 c 1 , ... , c p c_1, ..., c_p c1,...,cp。WSCP 的目标是从 S S S 中选取一个成本最小的子集合集，使其覆盖 Ω \Omega Ω 的所有元素。也就是说，我们旨在找到一个 S S S 的子集 S ′ S' S′，使得
- S ′ S' S′ 中所有集合的并集包含了 Ω \Omega Ω 的每个元素。
- S ′ S' S′ 中集合的总权重最小化。
从数学上来说，如果我们用 x i ( i = 1 , ... , p ) x_i (i = 1, \dots , p) xi(i=1,...,p) 来表示集合 S S S 的子集 S i S_i Si 是否包含在 S ′ S' S′ 中（ x i = 1 x_i = 1 xi=1 表示包含, x i = 0 x_i =0 xi=0 则表示不包含），那么 WSCP 可以表述为

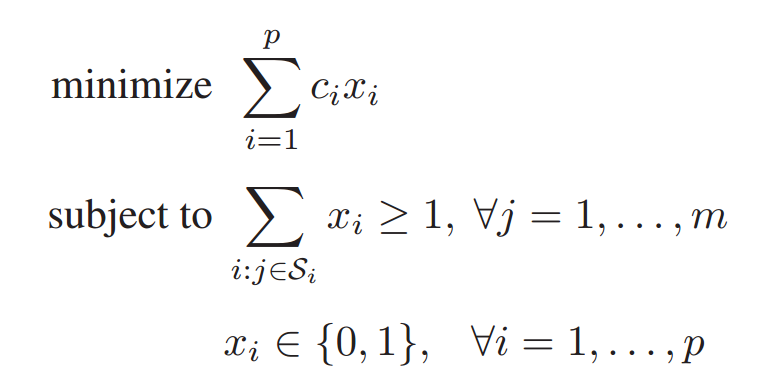
值得注意的是，WSCP 意味着 Ω \Omega Ω 中的每个元素可能存在于 S ′ S' S′ 的多个集合中。
聚类问题转化：为了将客户端聚类过程转化为 WSCP，首先将全集 Ω \Omega Ω 视为候选客户端的集合。此外， S S S 中的每个元素可以看作是一个潜在的客户端簇（即 Ω \Omega Ω 的一个子集）。本文允许具有不同类别数据样本的客户端同时被划分到多个中（即多样性优化的客户端聚类），这对应于 Ω \Omega Ω 中的每个元素可能同时存在于 S S S 的多个集合中。然后，客户端聚类过程等价于在 S S S 中寻找一个具有最小成本的子集 S i S_i Si。然而，要完成客户端聚类问题的转化，我们仍需解决以下三个问题：
- 候选集 S S S 的先验知识是未知的，因为聚类的数量和结构不可用。
- 每个聚类都应是唯一的，因为相同的聚类会产生冗余的类模型。
- 从 S S S 中选择某聚类 S i S_i Si的相关成本是未知的。
为解决上述问题，本文首先构建集合 S S S，即基于预先设定的数据分布相似性阈值 α \alpha α（由 ISM 衡量）来获取所有可能的簇。对于每个客户端 n ∈ N n \in N n∈N，其 ISM 值中高于 α \alpha α 的客户端将与客户端 n n n 一同被分入一个簇 S n S_n Sn，从而成为 S S S 的元素。通过这种方式，由于与多个客户端具有较高的数据分布相似性，拥有多中类别数据的客户端将加入多个簇中（算法2，第 1-- 8行）。随后，为了避免 S S S 中簇的冗余，我们对 S S S 进行了去重操作（算法2，第 9 行）。

接下来，需要适当地刻画集合 S S S 中每个簇的成本（算法2，第 10--13 行）。鉴于聚类的目标是将具有相似数据分布的客户端归为一簇，因此每个簇的成本应相应地反映其整体数据分布的相似性。具体而言，集合 S S S 中每个簇 S n S_n Sn 的成本 c ( S n ) c(S_n) c(Sn) 计算如下（代价函数）：
c ( S n ) = 1 ∑ j ∈ S n I S M n [ j ] c(S_n)=\frac{1}{\sum_{j\in S_n}ISM_n[j]} c(Sn)=∑j∈SnISMn[j]1

成本 c ( S n ) c(S_n) c(Sn) 表明总体数据分布相似性较大的簇具有较小的代价。

通过代价函数，WSCP的解对应于组覆盖所有客户端的聚类，并在整体上具有最高的簇内数据分布相似性。接下来，将展示如何获得该解。

客户聚类问题解决方案：WSCP 是 NP-困难问题，对于大规模实例已知的高算法可以求解。作为替代方案，我们了一种贪心解法。首先在定义 2 中定义 S S S 中每个候选簇 S n S_n Sn 的有效载荷。

定义2.（有效载荷）：对于 S S S 中的任意候选簇 S n S_n Sn，如果我们用 I \mathcal{I} I 表示已包含在所选簇中的客户端，则其有效载荷计算为
P a y l o a d ( S n ) = c ( S n ) ∣ S n ∖ I ∣ Payload(S_n)=\frac{c(S_n)}{|S_n \setminus \mathcal{I}|} Payload(Sn)=∣Sn∖I∣c(Sn)

该公式反映了在所选聚类中未被包含在 S n S_n Sn 中客户端的平均成本。

本文通过贪心算法来解决WSCP问题，贪心地（不放回地）逐个选择 S S S 中负载最小的候选簇，并将关联的客户端添加到 I \mathcal{I} I 中，直到 I \mathcal{I} I 覆盖所有客户端（算法2，第14-21行）。

事后攻击检测

一种针对分布式攻击的直接防策略是在每轮集群模型聚合之前执行恶意模型检测，但这会给模型训练带来大量额外开销，尤其是在大规模聚类联邦学习中。对于恶意集群攻击，现有的检测方案（假设良性客户端占多数）在识别恶意集群中的恶意客户端模型时具挑战性。

一种方法是直接丢弃恶意集群（在识别出后），但这种粗略的操作会抹去良性客户端对模型的贡献，从而导致在 non-IID 环境下模型的偏差。

为了解决上述问题，本文提出了一种 事后恶意簇攻击检测 机制，用于在识别出恶意簇攻击和分散攻击后检测恶意客户端模型。服务器会持续监测全局模型的准确率。当发现准确率下降时，将基于一个 小型公共数据集 对接收到的簇模型进行测试。随后，事后检测机制将被激活并按如下方式执行：

步骤1：对于每个恶意簇 C M = { 1 , . . . , M } C_M = \{1, . . . , M\} CM={1,...,M}，服务器选择不在该恶意簇中的且与该簇内客户端最相似的 d d d 个客户端，组成一个验证委员会。步骤 1详细过程如下所述：

当 C M C_M CM 中的客户端数量小于总客户端数量的 50%（即 M < N / 2 M < N/2 M<N/2）且大于预定义的验证委员会规模时，对于 C M C_M CM 中的每个客户端 m m m，选择 C M C_M CM 外与客户端 m m m 相关的 ISM 值最大的客户端作为候选验证委员会成员。否则，直接选择 C M C_M CM 外的全部 N − M N − M N−M 个客户端作为候选验证委员会成员（算法2，第 1--15 行）。
计算 C M C_M CM 中所有客户端与每个候选验证委员会成员 v i v_i vi 之间的整体数据分布相似性（算法3，第 16--18 行）。形式化地，对于每个 v i v_i vi，有
S i m v i = ∑ m = 1 M M s i m [ m ] [ v i ] Sim_{v_i}=\sum_{m=1}^M M_{sim}[m][v_i] Simvi=m=1∑MMsim[m][vi]
为了获得更可靠的检测结果，从这些候选验证委员会成员中选择具有最大 S i m v i Sim_{v_i} Simvi 的 d d d 个客户端以组成最终的委员会（算法3，第19-20行）。

步骤 2：在为每个检测到的恶意簇建立验证委员会之后，这些簇内的客户端需要将其本地模型发送到相应的验证委员会进行评估。由于委员会成员可能会从模型参数中推断出客户隐私，恶意簇中的客户端在共享参数之前使用高斯噪声来保护其隐私。

步骤3：每个委员会成员使用其本地数据来测试从恶意簇中的客户端接收到的模型。然后，委员会成员根据各自情况单独判定一个是恶意还是良性。

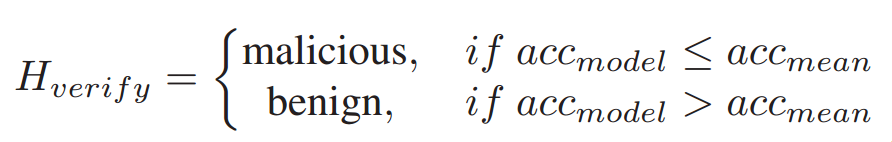
其中， a c c m o d e l acc_{model} accmodel 代表由委员会成员评估的模型的测试准确性， a c c m e a n acc_{mean} accmean 是同一委员会成员审查的所有模型的平均测试准确性。

步骤4：完成验证后，验证委员会成员对恶意簇群中的客户端进行投票。超过半数委员会成员认定为恶意的客户端将被弃置。其余被视为良性的客户端被汇集到一个新的集群中，以参与后续的联邦学习过程。