文章目录
向量的数量积
(这个定义可以参考高等数学中学习过的内积来理解)
假设x=(x1,x2······xn)T,y=(y1,y2······yn)T,且都∈Rn,或(Cn),把实数(x,y)=∑i=1n xiyi称为向量x与y的数量积,或者叫内积。
欧式范数
非负实数||x||2=(x,x)1/2 = (∑ i=1n xi2 )1/2 称为向量x的欧式范数
向量数量积的性质
(x,x)=0
(αx,y)= α(x,y)
(x,y)= (y,x)
(x1+x2,y)= (x1,y)+(x2,y)
|(x,y)| ≤ ||x||2 ||y||2
||x + y||2≤ ||x||2 + ||y||2(三角不等式)
向量范数的极限
在R中定义了实值函数,记作||·||,对所有的x,y∈ Rn,以及λ∈ R,如果满足:
1,||x|| ≥ 0,当且仅当x=0时, ||x|| = 0(即:非负性)
2,||λx||= | λ | || x ||(即:齐次性)
3, ||x + y||≤ ||x|| + ||y||(三角不等式)
那就称||x||是向量x的范数(或者模)
常用的范数
向量的♾️-范数(也叫做最大范数):||x||♾️= max 1≤i≤n |xi|
向量的 1- 范数(也叫做绝对值范数) :||x||1 = ∑i=1 n|xi|
向量的 2 -范数:||x||2 = (x,x)1/2 = (∑ i=1n xi2 )1/2 (就是向量本身的平方和再开二次根)
向量的 p -范数:||x||p = = (∑ i=1n xip )1/p ,1 ≤ p ≤♾️。
当 p=1 时,就是 1 范数,当 p=2 时,就是 2 范数。
向量序列的极限
假设{x(k)}是Rn中的一个向量序列, x*∈Rn,记:x(k)=( x1(k) , x2(k) ······ xn(k) )T,x*=( x1* , x2* ······ xn* )T,若limk→♾️ xi(k) = xi* (i=1,2,3······n),就称向量序列{xi(k)}收敛于x*。
只看官方定义不是很好理解的话,就看下面这个表格:
| x(1) | x(2) | x(k) | ------> | x* |
|---|---|---|---|---|
| x1(1) | x1(2) | x1(k) | ------> | x1* |
| x2(1) | x2(2) | x2(k) | ------> | x2* |
| x3(1) | x3(2) | x3(k) | ------> | x3* |
范数的连续性(定理1)
Rn中的任何范数||x||都是x的连续函数。
范数的等价性(定理2)
设||x||s,||x||t是Rn中的任意两种范数,>则存在常数c1,c2>0,使得:
c1||x||s≤||x||t≤c2||x||s,对一切x∈Rn
(其实这个式子表达的是任意两个范数之间相差不超过一个常数倍)(也可以看出在一种范数意义下向量序列收敛,那么在任何一种范数意义在这个向量序列也收敛)
定理3
limk→♾️ x(k) = x*的充要条件是limk→♾️ ||x(k) - x*|| = 0,其中||·||是向量的任一种范数。
(这个定理常用来判断向量序列的收敛。)
矩阵范数
在Rn×n中定义了实值函数,记作||·||,对所有的A,B∈Rn×n,以及λ∈R,如果满足:
1,||A|| ≥ 0,当且仅当A=0时, ||A|| = 0(即:非负性)
2,||λA||= | λ | || A ||(即:齐次性)
3, ||A + B|≤ ||A|| + ||B||(三角不等式)
4,||A B|| ≤ ||A|| ||B||
那就称||A||是矩阵A的范数。
相容性
(在大多数情况在,矩阵和向量会同时出现,因为它有相容性)
假设矩阵范数||·||s,向量范数||·||t,如果对于任何向量x∈Rn,以及矩阵A∈Rn×n,都有:
||Ax || t≤ ||A|| s||x||t
成立,那么就称矩阵范数||·||s与向量范数||·||t相容。
从属范数
设||·||是Rn中的向量范数,对于任何A∈Rn,若定义:
||A|| = max||x||=1||Ax||
那么||A||是矩阵A的范数,则矩阵范数||·||称为向量范数||·||的从属范数。矩阵范数与向量范数相容。也就是有:
||Ax|| = ||A|| ||x||
(Ax,x都是向量范数,A是矩阵范数)
常用的矩阵范数
♾️-范数(行范数):||A||♾️=max1≤i≤n∑j=1n
|aij|,从属于向量的♾️-范数的矩阵范数。
(先计算每一行上元素绝对值的行和)
1 -范数(列范数):||A||1=max1≤j≤n∑i=1n
|aij|,从属于向量的1-范数的矩阵范数。
(先计算每一列上元素绝对值的列和)
2-范数(谱范数):||A||2=√λmax(ATA),是从属于向量的2-范数的矩阵范数。其中,λmax是矩阵ATA的最大特征值。
F-范数:||A||F=[∑ i,j=1 n aij 2]1/2,是与向量的2-范数相容的矩阵范数,但不是从属范数。
举个例子:
计算A的常用范数。
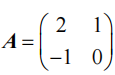
解析:
1,A的♾️-范数(行范数):由于A的第一行绝对值之和是3,第二行绝对值之和是1,所以取最大的为3,因此无穷范数就是3。
2,A的1-范数(列范数):由于A的第一列绝对值之和是3,第二列绝对值之和是1,所以取最大的为3,因此1-范数就是3。
3,A的2-范数(谱范数):计算过程如下:
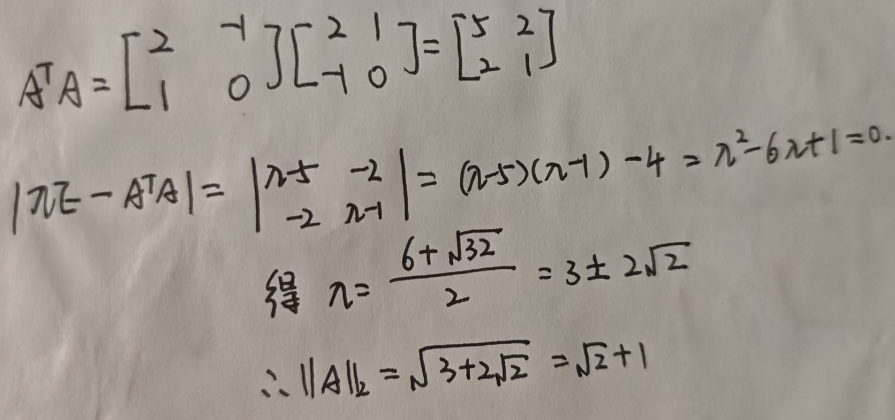
4,F-范数:
所有元素的平方和是6,所以对6开二次跟即可。
因此:
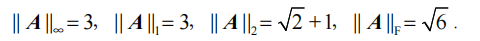
谱半径
矩阵 A∈Rn的特征值按模最大值称为 A 的谱半径,记为 ρ(A) ,即 ρ(A) =max 1≤i≤n |λi|,式中,λi是 A 的特征值.
谱半径是所有函范数的下界
A 的 2-范数与该矩阵的谱半径相等
A²的谱半径就是谱半径²
未完待更~~~
:)