01数据结构-01背包问题

问题引入
1.问题描述
2.经典案例
3.01背包代码实现

问题引入

今年过去的 "双十一" ，你有薅到羊毛吗？

每年的双十一，会有各种促销活动，比如 "满 300元减 80 元"。假如你女朋友的购物⻋中有 n 个（n > 100）想买的商品，她希望从里面选几个，在凑够满减条件的前提下，让选出来的商品价格总和最大程度地接近满减条件（300 <= price <= 380），这样就可以极大限度地"薅羊毛"。作为一名 "聪明" 的程序员，你有想过编程帮她搞定吗？

要想高效地解决这个问题，就要用到我们今天讲的 01 背包问题（0-1 Knapsack

Problem）。首先记住一点，01 背包问题不是一个问题，而是一类动态规划问题，很多动态规划问题都可以抽象成 01 背包问题。

1.问题描述

给定n件不可分割的物品和一个背包。物品i的重量是 w[i] ，其价值为 v[i] ，背包的容量为c 。问应如何选择装入背包中的物品，使得装入背包中的物品在不超过背包容量的情况下总价值最大？在选择装入背包的物品时，对每种物品i只有两种选择，即装入背包（1）和不装入背包（0）。不能将物品装入背包多次，也不能只装入商品的一部分（商品不可分割）。这就是经典的 0-1 背包问题。接下来来看一个案例

2.经典案例

现在，我们将题目中的物品价值暂时去掉了，这样更方便我们掌握动态规划和 01 背包问题，我们先考虑用递归对问题进行解决。假设背包容量为10，有5个物品，每一个物品的重量{2，2，4，6，5}

暴力递归就是枚举物品集合的所有子集，并计算每一个子集的总重量，最后选择与背包的总容量c最接近的子集即为最优解。

考虑物品的最优子集，对于每一个物品i均有下面两种情况。

1、物品i包含在最优子集中

2、物品i不包含在最优子集中。

递归树中的每一个结点表示一种状态，我们用 (i, w) 来表示，其中，i 表示将要决策的第 i 个物品是否装入背包，w 表示当前背包中物品的总重量。比如，(3,8) 表示我们要决策的物品第 3 个物品（重量为 4）是否装入背包，决策后，将其装入背包，当前背包的重量为 8；(3,4) 则表示我们当前要决策的物品是第 3 个物品，在决策后，不将其装入背包，当前背包的重量为 4。

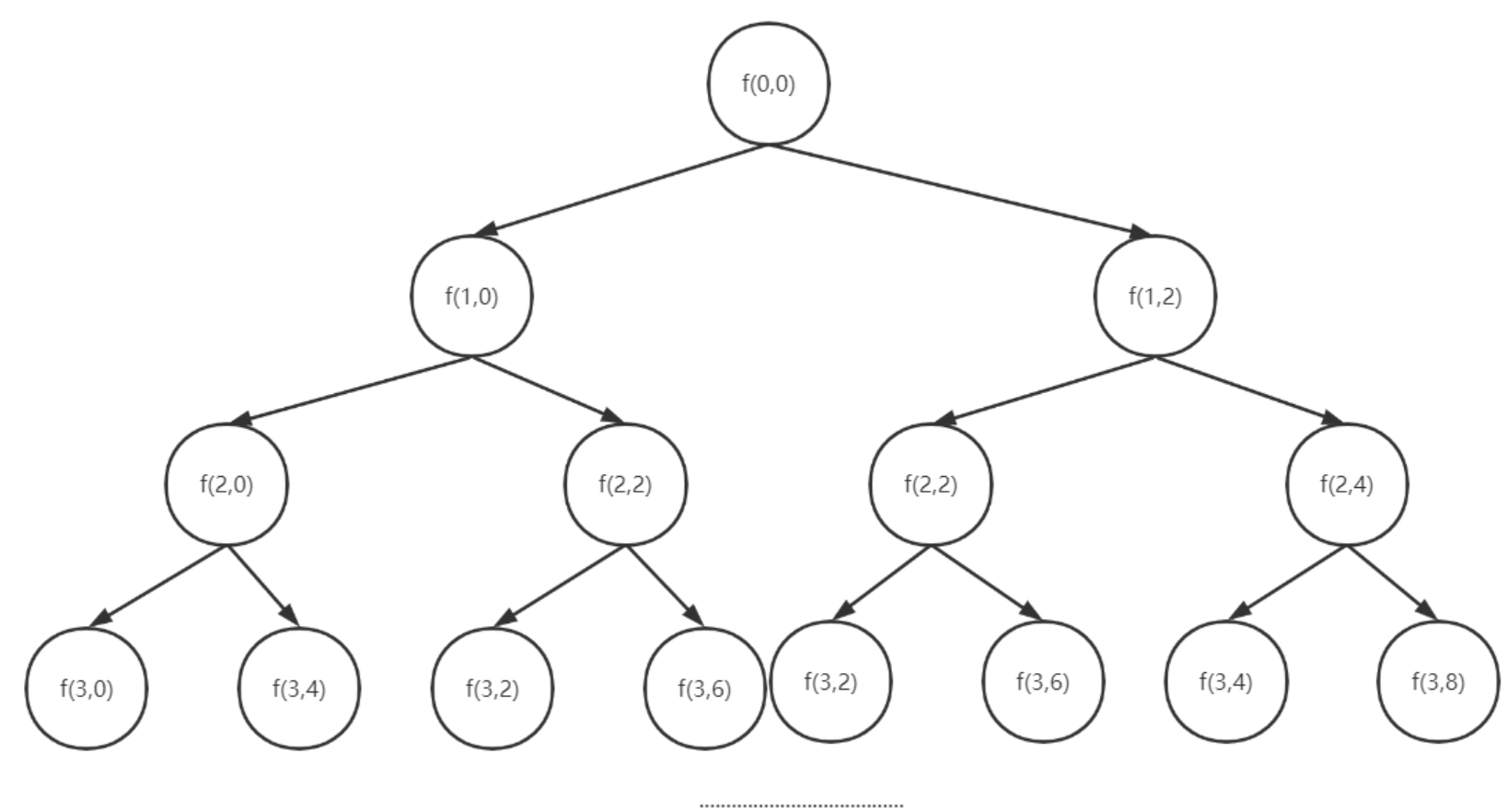
如果添加第 n 个物品后，背包的重量超过了总容量c ，则第 n 个物品就不能装入背包；否则，则可以将第 n 个物品装入背包。

回顾一下递归的三要素：

第一：明确你写的递归函数想要干什么，即函数功能；

第二：找到递归的结束条件；

第三：找出函数的等价关系式。

简易代码：

c 复制代码

int maxW = -1; // 保存背包中可容纳的最大重量
int[] wt = {2,2,4,6,5}; //表示每一个物品的重量
n = 5; 	// n 表示物品总数
c = 9;     // c 背包容量 
// w 表示当前已经装进背包的物品的总重量; i表示考察到了哪个物品
//第一要素：函数功能，决定是否将第 i 个物品装入背包，从而获得最大重量
void Knapsack(int i, int w){
    //递归结束条件
	if(w == c || i == n){ // w == c 表示装满了，i == n 物品考察完了
		if(w > maxW){
			maxW = w;
        }
        return;
    }
    // 等价关系式，装 or 不装
    Knapsack(i+1, w); // 选择不装第 i 个物品
    if(w + wt[i] <= c){
       Knapsack(i+1, w + wt[i]); // 选择装第 i 个物品。
    }
}
//调用
knaspsack(0,0);

显而易⻅，递归树中有很多子问题被重复计算，比如图中的 f(2,2) 和 f(3,4) 均被重复

计算了两次。

要对这些重复计算的结点进行剪枝，我们就可以使用 DP Table 和备忘录方法。

"备忘录" 方法，就是将已经计算好的子问题的解 f(i, w) 保存起来，当再次计算到重复的 f(i, w) 时，直接从备忘录中取出来用就行了，不用再递归计算，这样就有效地避免重复计算，达到剪枝效果。这里仅介绍备忘录方法

c 复制代码

int maxW = -1; // 保存背包中可容纳的最大重量
int wt[] = {2, 2, 4, 6, 5}; // 物品重量数组
int n = 5; // 物品总数
int c = 9; // 背包容量

bool memo[5][10]; // 记忆化数组

void Knapsack(int i, int w) {
    // 递归结束条件
    if (w == c || i == n) {
        if (w > maxW) {
            maxW = w;
        }
        return;
    }
    // 如果已经计算过这个状态，直接返回
    if (memo[i][w]) {
        return;
    }
    // 标记当前状态已计算
    memo[i][w] = true;
    // 不选择第i个物品
    Knapsack(i + 1, w);
    // 选择第i个物品（如果不超重）
    if (w + wt[i] <= c) {
        Knapsack(i + 1, w + wt[i]);
    }
}

// 初始化记忆化数组
void initMemo() {
    for (int i = 0; i < n; i++) {
        for (int j = 0; j <= c; j++) {
            memo[i][j] = false;
        }
    }

一共5个物品，背包中重量是9，我们也可以选择什么都不放，所以我们memo是[5][10]这样我们就存放了所有可能的数据。由于这并不是真正的01背包，所以只是介绍一下，接下来，我们来分析下面这个经典案例。

如图初始有这些物品的重量和价值，如果我们按照贪心算法，那我们会选择两个前价值/重量大的物品，此时重量为3，总价值为16，无法放入第三个，但这明显是错的，因为id1和id2对应的价值加起来的和是22，才是我们背包应该放的两件物品。所以此时贪心算法并不能给出最优解，我们在高中学数学的时候经常听到极值和最值，极值是在某个区间内的最大值，最值是在整个区间内取的最大值。此时的贪心算法就对应的最值，接下来我们来分析如何解决这种类型的题目。

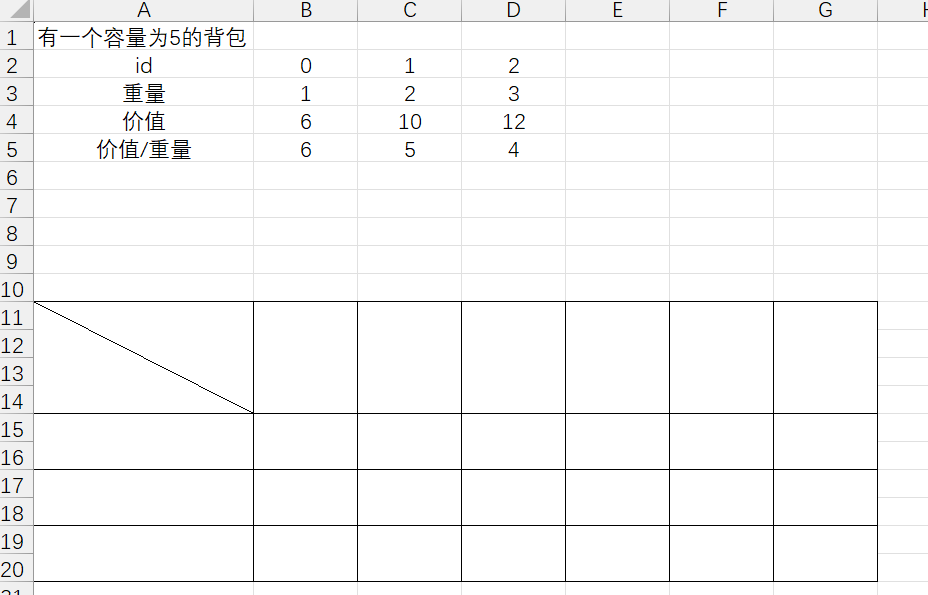
如图，假设有n个物品，数组中的元素代表n个物品中的各个物品，0代表该物品不放入背包，1代表该物品放入背包，很明显每个数组元素的值要么是1要么是0，既然如此，根据高中学的排列组合，我们很容易就能得出总的组合有2ⁿ种，由于我们的物品对应有价值，那么我们的最值就一定在这2ⁿ种的组合里面，但是要注意，我们的物品不光有价值，还有重量，在这2ⁿ种组合里面，我们只能取那些加起来的重量和没有超过背包重量的组合，在这些组合里寻找最值。

我们写这么一个函数F(n,C)考虑将n个物品放入容量为C的背包里的价值，价值最大 。F(i,C)=max{不装入i,装入i}，即F(I,C)=max{F(i-1,C)，v(i)+F(i-1,C-w(i))}，可能这样看上去有点不懂，接下来我来画一下递归树：

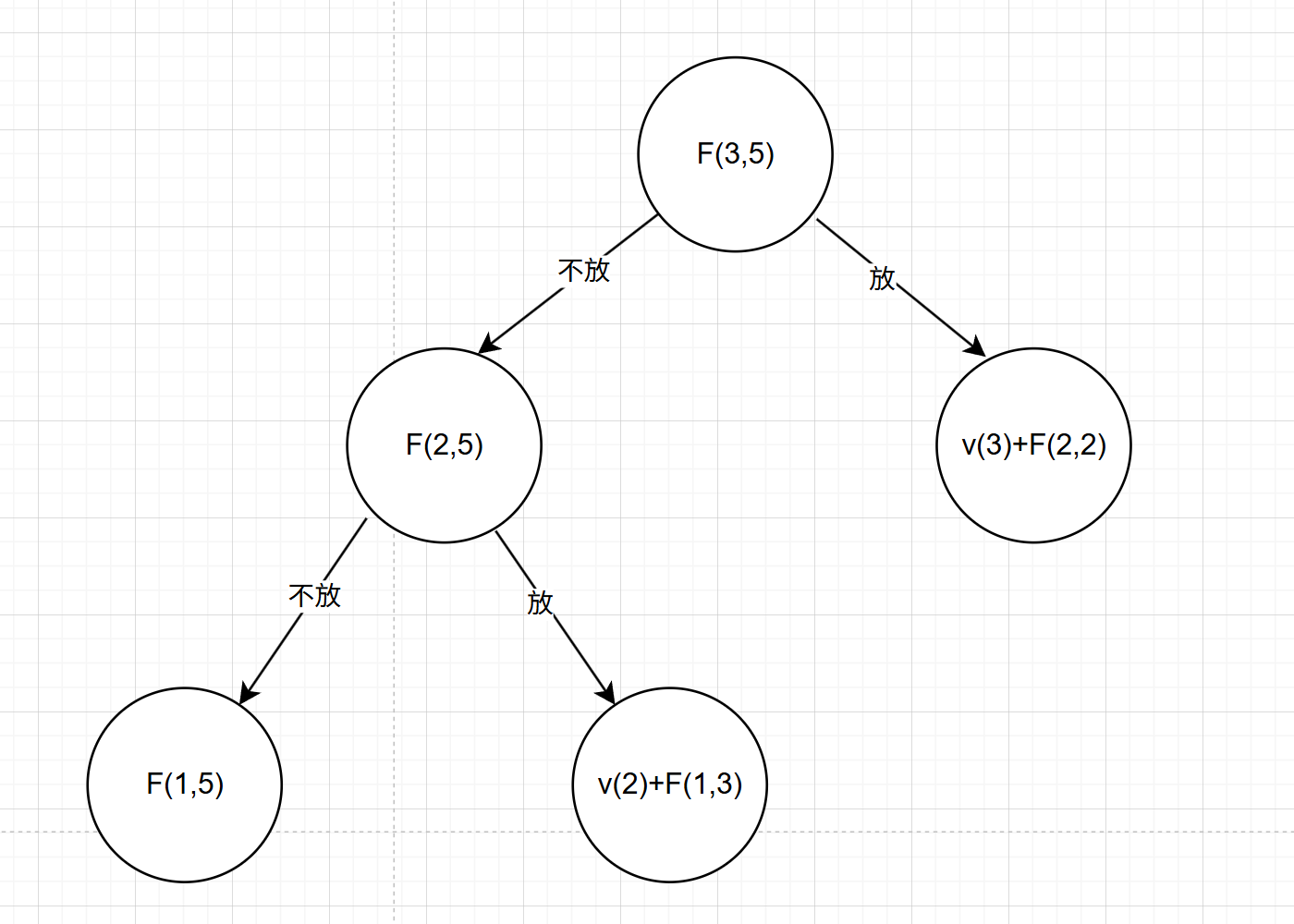
要求背包容量为5，物品个数为3的01背包问题，我们只需知道

不放3的情况下，意味着第三个物品的价值是不管的，那么前面的最优结果是有两个物品，背包容量为5的结果

放第3个物品的，第三个物品的价值(v(3))要装入，再加上前面两个物品用背包容量为5-3=2的最优解，因为已经装入了第三个物品的容量，所以最优结果的参数要减去3。

这样就构成了递归树。

如图，当要放入物品id为0时，如果背包的重量是0，很明显放不进去，如果背包重量是1-5，都能放入，且最有价值为6。

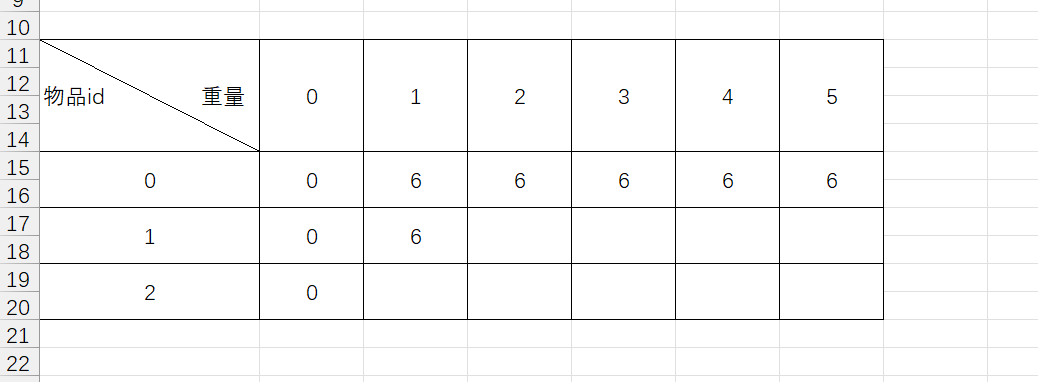
如图，同理当背包容量为0的时候，1号和2号物品也放不进去，当背包容量为1的时候，此时我们可以有两种选择，一种是选择不放1，那么最优值是F(0,1)，如果放入物品2，发现物品2重2放不进去，我们取最优解，肯定是F(0,1)。

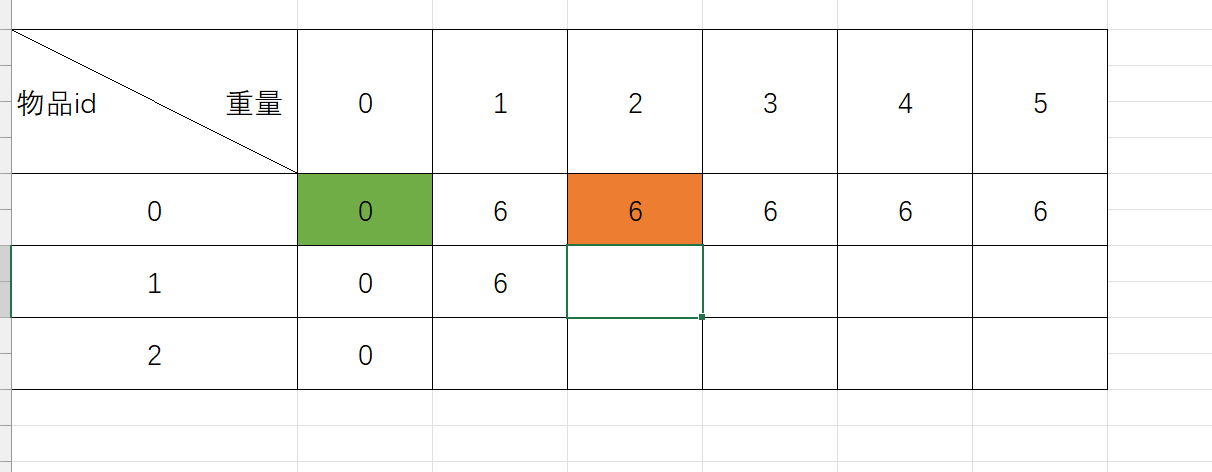
当我们要在背包容量为2的情况下放入物品id1的时候，我们要么不放入1，此时最优结果F(0,2)是图中橙色区域对应部分，要么放入1，此时最优结果是放入1后1的价值加上背包容量减去1的重量的背包容量作为F()的参数，即F(0,0)图中绿色部分，明显0+10>6，所以此时我们填写的是10。依次类推，最后的表格如图所示：

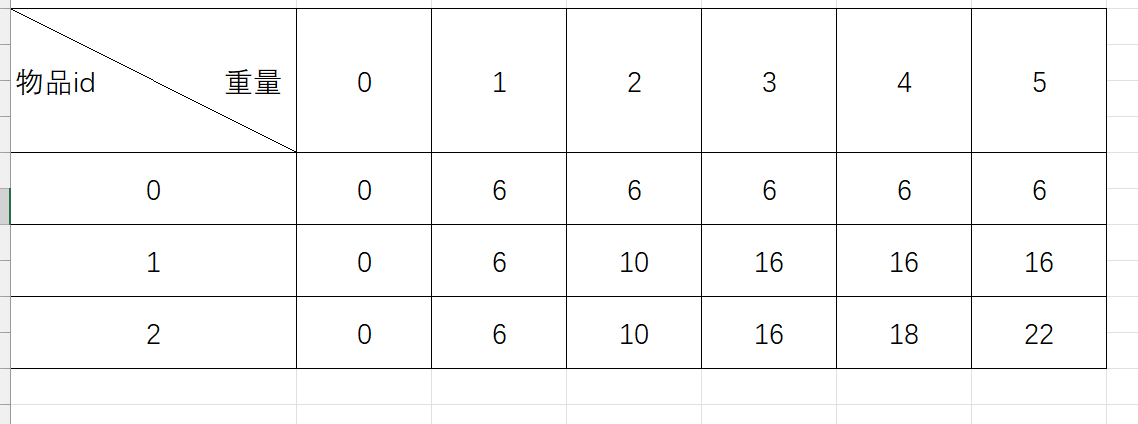
3.01背包代码实现

1.暴力递归法

c 复制代码

#include <stdio.h>
#include <stdlib.h>

static int wt_goods[] = {1, 2, 3};		// 重量
static int val_goods[] = {6, 10, 12};	// 价值
static int bag_capacity = 5;			// 背包容量

static int max(const int a, const int b) {
	return (a > b) ? a : b;
}

// 用[0...index]的物品，填充容积为c的背包的最大值
static int bestValue(int index, int c) {
	if (index < 0 || c <= 0) {		// 无法选物品，无法装入物品，返回0
		return 0;
	}
	// 不装入背包，只考虑[0...index-1]这么多物品来填充容积为c的背包
	int res = bestValue(index - 1, c);
	// 当前背包能容纳下index这个物品
	if (c >= wt_goods[index]) {
		res = max(res, val_goods[index] + bestValue(index - 1, c - wt_goods[index]));
	}
	return res;
}

int knapsack01() {
	return bestValue(sizeof(val_goods)/sizeof(val_goods[0]) - 1, bag_capacity);
}

首先我们定义三个全局变量，物品的重量，价值和背包的容量，我们写第一个01背包代码，写一个内在接口函数，用于处理核心代码，由于数组是从0开始的，我们把第一个物品认为是数组中的0元素，故在int knapsack01()函数中传入背包总容量bag_capacity参数和sizeof(val_goods)/sizeof(val_goods[0]) - 1参数。

核心接口：

第一个分支不装入背包，只考虑[0...index-1]这么多物品来填充容积为c的背包

第二个当前背包能容纳下index这个物品，装入背包，则我们判断两种分支谁的价值更大，此时由于我们是C语言，需要自己写一个max函数，写好之后按照上面写的逻辑，用代码实现即可。

注意由于是递归函数，记得写递归终止条件，这里的递归终止条件很明显是背包容量不能小于等于0，物品index不能小于0。

在int knapsack01()调用，返回对应的值即可。

测试一下：

c 复制代码

int main() {
	int result = knapsack01();
	printf("value = %d\n", result);
	return 0;
}

结果：

c 复制代码

D:\work\DataStruct\cmake-build-debug\06_DP\knapsack.exe
value = 22

进程已结束，退出代码为 0

2.记忆化搜索表法

c 复制代码

static int bestValue02(int index, int c, void *data) {
	int (*mem)[bag_capacity + 1] = data;
	if (index < 0 || c <= 0) {
		return 0;
	}
	if (mem[index][c] != -1) {
		return mem[index][c];
	}
	int res = bestValue02(index - 1, c, mem);
	if (c >= wt_goods[index]) {
		res = max(res, val_goods[index] + bestValue02(index - 1, c - wt_goods[index], mem));
	}
	mem[index][c] = res;
	return res;
}
int knapsack02() {
	int n = sizeof(val_goods) / sizeof(val_goods[0]);
	int (*mem)[bag_capacity + 1] = malloc(n * sizeof(*mem));
	for (int i = 0; i < n; ++i) {
		for (int j = 0; j <= bag_capacity; ++j) {
			mem[i][j] = -1;
		}
	}
	int result = bestValue02(sizeof(val_goods)/sizeof(val_goods[0]) - 1, bag_capacity, mem);
	free(mem);
	return result;
}

在int knapsack02()里面申请一个二维数组，初始化这个二维数组中的元素都为-1（默认为暂时没有填充数据）用result接收最后在核心接口static int bestValue02(int index, int c, void *data) 返回出来的数。

在核心接口里，由于我们写的参数是void *，所以我们需要在核心接口里面需要创建一个临时变量来接收传入的二维数组，其他的代码跟上节课的记忆化搜索表法一个思路。

注意这里 int (*mem)[bag_capacity + 1] = data;传入的是地址，所以即使函数结束也能修改该原始数据。

测试一下：

c 复制代码

int main() {
	int result = knapsack02();
	printf("value = %d\n", result);
	return 0;
}

结果：

c 复制代码

D:\work\DataStruct\cmake-build-debug\06_DP\knapsack.exe
value = 22

进程已结束，退出代码为 0

3.DP table

c 复制代码

int knapsackDP(int n, int c) {
	int (*dp)[c + 1] = malloc(sizeof(int) * n * (c + 1));
	// 初始化第一行
	for (int i = 0; i <= c; ++i) {
		dp[0][i] = (i >= wt_goods[0]) ? val_goods[0] : 0;
	}
	for (int i = 1; i < n; ++i) {
		for (int j = 0; j <= c; ++j) {
			dp[i][j] = dp[i - 1][j];
			if (j >= wt_goods[i]) {
				dp[i][j] = max(dp[i][j], val_goods[i] + dp[i - 1][j - wt_goods[i]]);
			}
		}
	}
	
	int res=dp[0][0];
	for (int i = 0; i < n; ++i) {
		for (int j = 0; j <= c; ++j) {
			if (dp[i][j]>res) {
				res=dp[i][j];
			}
		}
	}
//	int res = dp[n - 1][c];
	free(dp);
	return res;
}

由于不需要递归，我们也不需要写static静态函数了，我们需要初始化第一行，初始化方法是如果当前你的背包容量能够存下第一个物品的重量，那么填入相应物品的价值，否则若不能存，就填入0。初始化完后开始后面的行数，从下一行开始根据上面所写的逻辑依次填入值，所以外层循环从1开始到第n个礼物，内层循环从0开始到背包容量为c，开始循环，其实就是我们填写这个表的过程：

先默认不装入时是最大的，然后再比较装入后两者的较大值。

有些情况下最大值可能不是在最后而在中间，只是这里比较碰巧，在最后返回这个表的最大值即可。

最后来测一下：

c 复制代码

int main() {
	int result = knapsackDP(sizeof(wt_goods)/sizeof(wt_goods[0]), bag_capacity);
	printf("value = %d\n", result);
	return 0;
}

结果：

c 复制代码

D:\work\DataStruct\cmake-build-debug\06_DP\knapsack.exe
value = 22

进程已结束，退出代码为 0

大概先写这些吧，今天的博客就先写到这，谢谢您的观看。