二维伞的雨滴效应

一、题目描述

普通的伞在二维平面世界中，左右两侧均有一条边，而两侧伞边最下面各有一个伞坠子，雨滴落到伞面，逐步流到伞坠处，会将伞坠的信息携带并落到地面，随着日积月累，地面会呈现伞坠的信息。

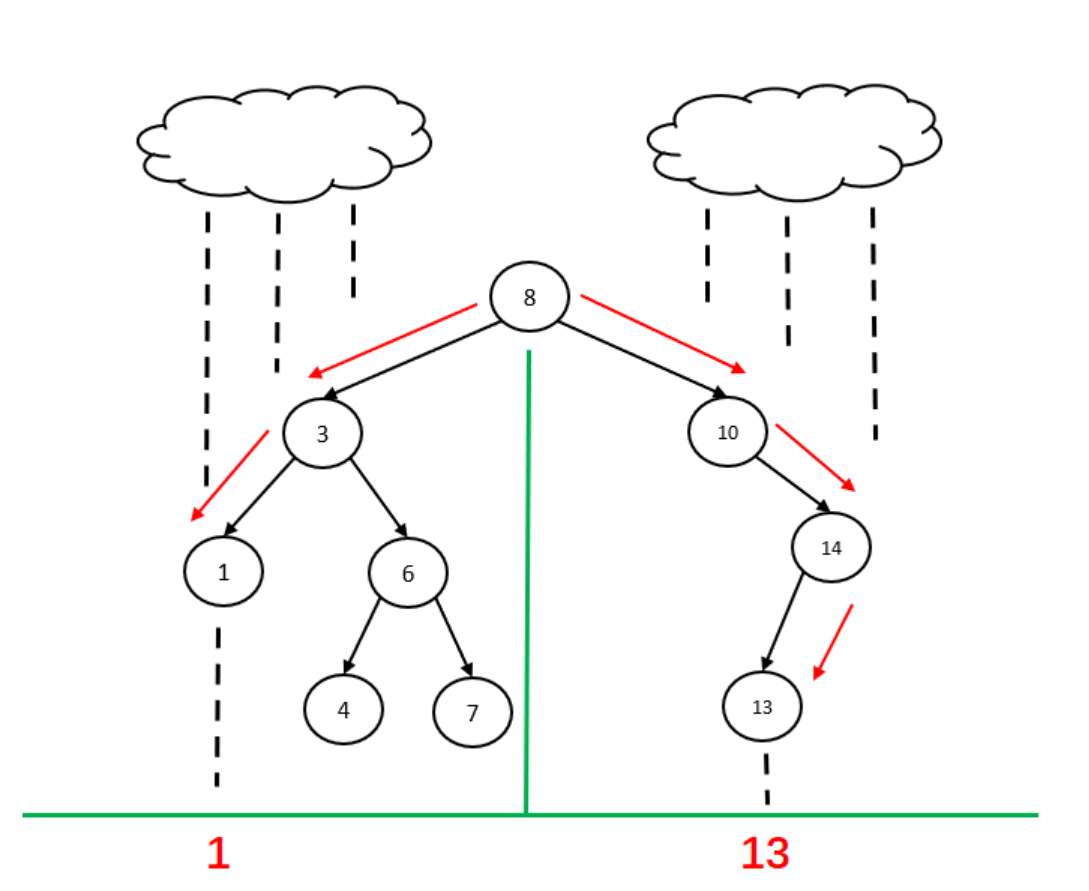
1、为了模拟伞状雨滴效应，用二叉树来模拟二维平面伞（如下图所示），现在输入一串正整数数组序列（不含0，数组成员至少是1个），若此数组序列是二叉搜索树的前序遍历的结果，那么请输出一个返回值1，否则输出0。

2、同时请将此序列构成的伞状效应携带到地面的数字信息输出来(左边伞坠信息，右边伞坠信息，详细参考示例图地面上数字)，若此树不存在左或右扇坠，则对应位置返回0。同时若非二叉排序树那么左右伞坠信息也返回0。

二、输入输出描述

输入描述

• 一个通过空格分割的整数序列字符串，数组不含0，数组成员至少1个，输入的数组的任意两个数字都互不相同，最多1000个正整数，正整数值范围1~65535

输出描述

• 输出如下三个值，以空格分隔：是否二叉排序树，左侧地面呈现的伞坠数字值，右侧地面呈现的伞坠数字值。

  若是二叉排序树，则输出1，否则输出0（其左右伞坠值也直接赋值0）。

  若不存存在左侧或者右侧伞坠值，那么对应伞坠值直接赋值0。

三、示例

|----|--------------------------------------------------|
| 输入 | 8 3 1 6 4 7 10 14 13 |
| 输出 | 1 1 13 |
| 说明 | 1表示是二叉搜索树前序遍历结果，1表示左侧地面呈现的伞坠数字值，13表示右侧地面呈现的伞坠数字值 |

四、解题思路

1. 核心思想

利用二叉搜索树（BST）的特性 + 前序遍历的 "根左右" 规则，先验证给定序列的合法性并同步还原二叉搜索树；若合法，再通过优先左 / 右子树的递归遍历，找到树的左、右缀点，最终按格式返回结果。核心是 "特性驱动验证与还原，优先遍历驱动缀点查找"。

2. 问题本质分析

• 表层问题：验证前序遍历序列是否为合法 BST，并查找 BST 的左、右缀点；
• 深层问题：

1. 序列合法性验证：本质是利用 BST 和前序遍历的双重特性，划分左、右子树区间并校验区间合法性；
2. 二叉树还原：在验证合法性的过程中，通过递归创建左、右子节点，完成树的构建，为后续缀点查找提供载体；
3. 缀点查找：本质是寻找二叉树的最底层节点，同时保证 "最左" 或 "最右"，需通过优先左 / 右子树的递归遍历实现；
4. 边界处理：单个节点（根节点）无左右缀点，需返回 0；序列非法时返回固定格式结果。

3. 核心逻辑

• 合法性验证与树还原：

1. 以 "根左右" 规则为基础，前序序列首元素为根节点；
2. 利用 BST 特性划分左、右子树区间（左子树值 <根，右子树值> 根）；
3. 校验右子树区间的合法性，再递归处理左、右子树，同步创建子节点完成树还原；

• 缀点查找：

1. 左缀点：优先递归左子树，无左子树时递归右子树，直到找到最底层节点；
2. 右缀点：优先递归右子树，无右子树时递归左子树，直到找到最底层节点；

• 结果输出：根据验证结果，返回合法格式（1 + 左右缀点）或非法格式（0 0 0）。

4. 步骤拆解

1. 输入解析与根节点初始化

   • 读取输入字符串，转换为前序遍历整数数组；
   • 以数组首元素为值，创建二叉搜索树的根节点。

2. 序列合法性验证与二叉树还原

   • 调用isValid方法，传入根节点和序列全区间（0 ~ 数组长度 - 1）；
   • 单个节点直接返回合法；
   • 查找左、右子树分界点i，校验右子树区间合法性（所有值 > 根节点）；
   • 存在左子树时，创建左子节点并递归验证左子序列；
   • 存在右子树时，创建右子节点并递归验证右子序列；
   • 若所有区间都合法，完成树的还原，返回 true；否则返回 false。

3. 左、右缀点查找

   • 验证合法时，调用getFarLeftBottomVal优先左子树递归，找到左缀点；
   • 调用getFarRightBottomVal优先右子树递归，找到右缀点；
   • 仅根节点时，两个缀点均返回 0。

4. 结果组装与输出

   • 合法则组装字符串"1 左缀点 右缀点"，非法则组装"0 0 0"；
   • 输出最终字符串。

五、代码实现

import java.util.Arrays;
import java.util.Scanner;

public class Main {
  // 二叉树的节点类定义
  static class Node {
    int val; // 节点值
    Node left_child; // 当前节点的左子节点
    Node right_child; // 当前节点的右子节点

    public Node(int val) {
      this.val = val;
    }
  }

  // 二叉搜索树前序遍历的结果序列
  static int[] preOrder;

  public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);
    preOrder = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
    System.out.println(getResult());
  }

  public static String getResult() {
    // 二叉搜索树的根节点root
    Node root = new Node(preOrder[0]);

    if (isValid(root, 0, preOrder.length - 1)) {
      return 1 + " " + getFarLeftBottomVal(root, 0) + " " + getFarRightBottomVal(root, 0);
    } else {
      return "0 0 0";
    }
  }

  /**
   * 判断preOrder数组是否为合法的二叉搜索树前序遍历结果序列，如果是，则根绝preOrder还原出对应二叉搜索树
   *
   * @param root 二叉搜索树的节点，每个二叉搜索树节点都对应preOrder序列中的一段子序列
   * @param start 该子序列在preOrder中的范围的起始位置
   * @param end 该子序列在preOrder中的范围的结束位置
   * @return preOrder数组是否为合法的二叉搜索树前序遍历结果
   */
  public static boolean isValid(Node root, int start, int end) {
    // 如果当前节点对应的序列范围长度为1，则当前节点为叶子节点，无法继续递归，需要结束递归，而单个节点本身就是前序遍历结果，因此返回true
    if (start == end) return true;

    // 前序遍历即：根左右，因此start位置是当前序列对应的子树的根节点位置，当前子树的左子子树从start+1位置开始判断
    int i = start + 1;
    // 二叉搜索树的特点是：当前节点的左子节点值 < 当前节点的值
    while (i <= end && preOrder[i] < root.val) {
      i++;
    }

    // i 最终指向左右子树的分界位置
    int j = i;
    // 二叉搜索树的特点是：当前节点的右子节点值 > 当前节点的值
    while (j <= end && preOrder[j] > root.val) {
      j++;
    }

    // j 最终指向右子树的终点位置的后一个位置，而右子树的终点位置必须在end，因此合法的二叉搜索树前序遍历结果 j > end
    if (j <= end) return false;

    // i 最终指向左右子树的分界位置
    // 如果 i > start + 1，则存在左子树
    if (i > start + 1) {
      // 创建当前节点的左子树节点
      root.left_child = new Node(preOrder[start + 1]);

      // 递归判断左子树对应的序列范围是否为前序遍历结果
      if (!isValid(root.left_child, start + 1, i - 1)) {
        // 若不是，则preOrder无法还原出二叉搜索树
        return false;
      }
    }

    // i 最终指向左右子树的分界位置
    // 如果 i <= end，则存在右子树
    if (i <= end) {
      // 创建当前节点的右子树节点
      root.right_child = new Node(preOrder[i]);

      // 如果右子树对应的序列是合法的前序遍历结果，结合前面左子树对应的序列也是合法的前序遍历结果，则preOrder整体就是合法的前序遍历结果
      return isValid(root.right_child, i, end);
    }

    return true;
  }

  // 递归查找二叉树的左缀点，即二叉树最后一层中，最靠左的点
  public static int getFarLeftBottomVal(Node root, int level) {
    // 如果当前节点存在左子节点，则递归查找其左子节点
    if (root.left_child != null) {
      return getFarLeftBottomVal(root.left_child, level + 1);
    }

    // 如果当前节点没有左子节点，则检查当前节点处于哪一层
    if (level > 0) {
      if (root.right_child != null) {
        // 如果当前节点不处于第0层，且存在右子节点，则递归查找其右子节点
        return getFarLeftBottomVal(root.right_child, level + 1);
      } else {
        // 如果当前节点不处于第0层，且不存在右子节点，则当前节点即为左缀点
        return root.val;
      }
    } else {
      // 如果当前节点处于第0层，且没有左子节点，则没有左缀点，按题目要求返回0
      return 0;
    }
  }

  // 递归查找二叉树的右缀点，即二叉树最后一层中，最靠右的点
  public static int getFarRightBottomVal(Node root, int level) {
    if (root.right_child != null) {
      return getFarRightBottomVal(root.right_child, level + 1);
    }

    if (level > 0) {
      if (root.left_child != null) {
        return getFarRightBottomVal(root.left_child, level + 1);
      } else {
        return root.val;
      }
    } else {
      return 0;
    }
  }
}