PyTorch深度学习实战【11】之神经网络的学习和训练

缘友一世2025-09-24 15:21

文章目录

  • [一 梯度下降核心问题](#一 梯度下降核心问题)

    • [1.1 基本流程](#1.1 基本流程)
    • [1.2 权重迭代公式](#1.2 权重迭代公式)
    • [1.3 梯度与步长的定义](#1.3 梯度与步长的定义)

  • [二 梯度下降中的两个关键问题](#二 梯度下降中的两个关键问题)

    • [2.1 找出梯度向量的方向和大小](#2.1 找出梯度向量的方向和大小)
      • [2.1.1 交叉熵损失（Cross Entropy Loss）](#2.1.1 交叉熵损失（Cross Entropy Loss）)
      • [2.1.2 平方和误差（Sum of Squared Errors, SSE）](#2.1.2 平方和误差（Sum of Squared Errors, SSE）)
      • [2.1.3 损失函数的通用结构](#2.1.3 损失函数的通用结构)
      • [2.1.4 梯度下降算法的核心逻辑与关键问题](#2.1.4 梯度下降算法的核心逻辑与关键问题)
    • [2.2 让坐标点移动（进行迭代）](#2.2 让坐标点移动（进行迭代）)
      • [2.2.1 梯度下降与权重迭代](#2.2.1 梯度下降与权重迭代)
      • [2.2.2 jupyter中绘制代码](#2.2.2 jupyter中绘制代码)

  • [三 找出距离和方向：反向传播](#三 找出距离和方向：反向传播)

    • [3.1 方向传播的定义与价值](#3.1 方向传播的定义与价值)
      • [3.1.1 反向传播算法求 w ( 1 → 2 ) w^{(1\to 2)} w(1→2)导数](#3.1.1 反向传播算法求 w ( 1 → 2 ) w^{(1\to 2)} w(1→2)导数)
      • [3.1.2 反向传播算法求 w ( 0 → 1 ) w^{(0\to1)} w(0→1)导数](#3.1.2 反向传播算法求 w ( 0 → 1 ) w^{(0\to1)} w(0→1)导数)
    • [3.2 PyTorch实现反向传播](#3.2 PyTorch实现反向传播)

  • [四 移动坐标点](#四 移动坐标点)

    • [4.1 移动第一步](#4.1 移动第一步)
    • [4.2 从1到N：动量法](#4.2 从1到N：动量法)
    • [4.3 实现带动量的梯度下降](#4.3 实现带动量的梯度下降)

  • [五 开始迭代](#五 开始迭代)

    • [5.1 mSGD下降中的 `batch_size` 与 `epochs`](#5.1 mSGD下降中的 batch_size 与 epochs)
      • [5.1.1 batch_size（批量大小）](#5.1.1 batch_size（批量大小）)
      • [5.1.2 epochs（训练轮数）](#5.1.2 epochs（训练轮数）)
    • [5.2 二者关系](#5.2 二者关系)

  • [六 完整流程体验](#六 完整流程体验)

    • [6.1 完整代码(CPU版)](#6.1 完整代码(CPU版))
    • [6.2 完整代码(GPU版)](#6.2 完整代码(GPU版))

  • 在优化流程中，损失函数用于量化预测值与真实值的差异以评估模型优劣------损失越小则模型效果越好。目标是找到使损失最小的权重向量 w \boldsymbol{w} w。对于凸函数，导数为0的点为极小值点，数学上通常通过求导并令导数为0求解极值及对应 w \boldsymbol{w} w。但神经网络等复杂模型存在数百个权重，且交叉熵等复杂损失函数（机器学习中更复杂的函数亦然）使得直接令所有权重导数为0并逐个解方程难度大、工作量高。因此需转换思路：不追求一步到位，而是采用迭代方式逐步逼近损失最小值。这是优化算法的核心工作，其相关知识均围绕"逐步迭代至损失最小值"的具体操作展开。

一 梯度下降核心问题

1.1 基本流程

梯度下降是一种迭代优化算法，通过沿损失函数的负梯度方向更新参数，逐步逼近损失最小值。具体流程如下：

  • 初始化 ：随机设定初始权重向量 w 0 \boldsymbol{w}_0 w0；
  • 计算梯度 ：对当前权重 w t \boldsymbol{w}t wt，计算损失函数 L(\\boldsymbol{w}) 的梯度 ∇ w L ( w t ) \nabla{\boldsymbol{w}} L(\boldsymbol{w}_t) ∇wL(wt)（梯度方向为损失上升最快的方向）；
  • 更新权重 ：沿负梯度方向调整权重，得到下一轮权重 w t + 1 = w t − η ⋅ ∇ w L ( w t ) \boldsymbol{w}_{t+1} = \boldsymbol{w}t - \eta \cdot \nabla{\boldsymbol{w}} L(\boldsymbol{w}_t) wt+1=wt−η⋅∇wL(wt)（ η \eta η为学习率）；
  • 终止条件：重复上述步骤直至满足收敛条件（如梯度绝对值小于阈值、损失变化小于阈值或达到最大迭代次数）。

1.2 权重迭代公式

梯度下降中权重的迭代规则由学习率 η \eta η 和梯度 ∇ w L ( w ) \nabla_{\boldsymbol{w}} L(\boldsymbol{w}) ∇wL(w) 共同决定，标准公式为：
w t + 1 = w t − η ⋅ ∇ w L ( w t ) \boldsymbol{w}_{t+1} = \boldsymbol{w}t - \eta \cdot \nabla{\boldsymbol{w}} L(\boldsymbol{w}_t) wt+1=wt−η⋅∇wL(wt)

其中：

  • w t \boldsymbol{w}_t wt：第 t t t轮迭代的权重；
  • η \eta η：学习率（控制每步更新的步长，避免震荡或收敛过慢）；
  • ∇ w L ( w t ) \nabla_{\boldsymbol{w}} L(\boldsymbol{w}_t) ∇wL(wt)：损失函数在 w t \boldsymbol{w}_t wt处的梯度（反映损失对权重的瞬时变化率）。

1.3 梯度与步长的定义

  • 梯度 ：损失函数 L ( w ) L(\boldsymbol{w}) L(w)对权重向量 w \boldsymbol{w} w的一阶偏导数向量 ，记为 ∇ w L ( w ) = [ ∂ L ∂ w 1 , ∂ L ∂ w 2 , ... , ∂ L ∂ w n ] T \nabla_{\boldsymbol{w}} L(\boldsymbol{w}) = \left[ \frac{\partial L}{\partial w_1}, \frac{\partial L}{\partial w_2}, \dots, \frac{\partial L}{\partial w_n} \right]^T ∇wL(w)=[∂w1∂L,∂w2∂L,...,∂wn∂L]T。其物理意义是：在当前权重处，损失上升最快的方向（梯度的反方向为下降最快的方向）。
  • 步长 ：即学习率 η \eta η ，指每次迭代中权重更新的幅度。它决定了算法收敛的速度与稳定性：若 η \eta η过大，可能导致算法震荡甚至发散；若 η \eta η过小，则会减慢收敛速度。

二 梯度下降中的两个关键问题

2.1 找出梯度向量的方向和大小

  • 常见损失函数公式

2.1.1 交叉熵损失（Cross Entropy Loss）

  • 用于分类任务，衡量预测概率分布与真实标签分布的差异： C E L o s s = − ∑ i = 1 m y i ( k = j ) ln ⁡ σ i CE Loss = -\sum_{i=1}^m y_{i(k=j)} \ln \sigma_i CELoss=−∑i=1myi(k=j)lnσi
    • m m m：样本数量；
    • y i ( k = j ) y_{i(k=j)} yi(k=j)：第 i i i 个样本的真实标签（one-hot编码，仅正确类别为1，其余为0）；
    • σ i \sigma_i σi：第 i i i 个样本的预测概率（通过Softmax函数计算）： σ = s o f t m a x ( z ) \sigma = softmax(z) σ=softmax(z)， z = W X z = WX z=WX（ W W W 为权重矩阵， X X X 为特征张量）。

2.1.2 平方和误差（Sum of Squared Errors, SSE）

  • 用于回归任务，衡量预测值与真实值的差异： S S E = 1 m ∑ i = 1 m ( z i − z ^ i ) 2 SSE = \frac{1}{m} \sum_{i=1}^m (z_i - \hat{z}_i)^2 SSE=m1∑i=1m(zi−z^i)2
    • m m m：样本数量；
    • z i z_i zi：第 i i i 个样本的预测值（ z = X w z = Xw z=Xw， X X X 为特征矩阵， w w w 为权重向量）；
    • z ^ i \hat{z}_i z^i：第 i i i 个样本的真实值。

2.1.3 损失函数的通用结构

任意损失函数均包含三个核心元素：

  1. 特征张量 X X X：来自数据的输入特征；
  2. 真实标签 y / z y/z y/z ：来自数据的目标值（分类用 y y y，回归用 z z z）；
  3. 权重矩阵/向量 W / w W/w W/w：模型待学习的参数。
  • 给定一组权重 W / w W/w W/w，即可计算出损失函数的具体数值。当数据仅有一个特征时，权重 w w w 为标量，可绘制 w w w（横坐标）与 L ( w ) L(w) L(w)（纵坐标）的图像，直观展示损失随权重变化的趋势。
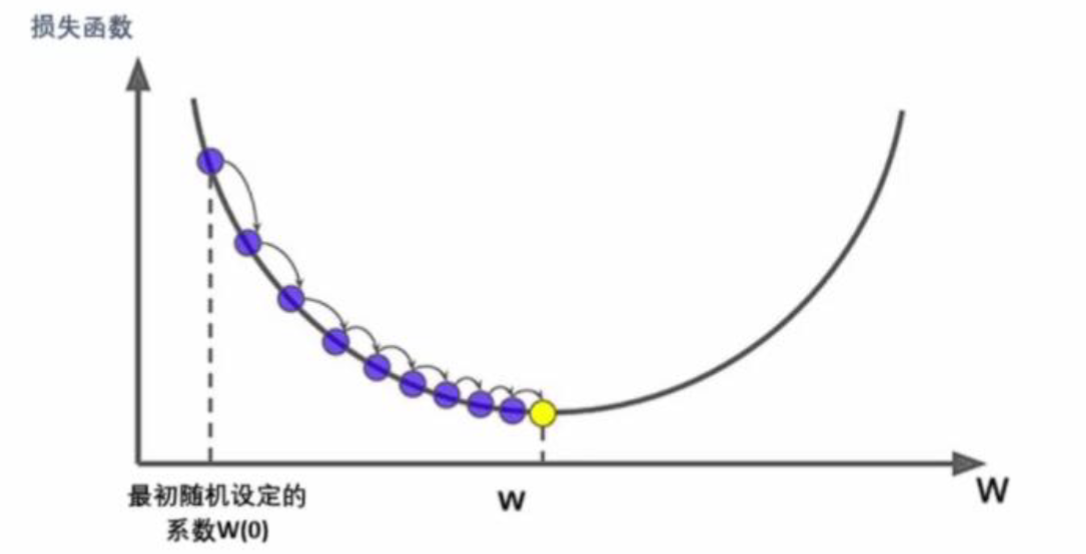
  • 在梯度下降的最开始时，我们会先随机设定初始权重 w ( 0 ) w_{(0)} w(0)，对应的初始损失函数值为 L ( w ( 0 ) ) L(w_{(0)}) L(w(0))，坐标点 ( w ( 0 ) , L ( w ( 0 ) ) ) (w_{(0)},L(w_{(0)})) (w(0),L(w(0)))就是梯度下降的起始点。从起始点开始，让自变量 w w w向损失函数 L ( w ) L(w) L(w)减小最快的方向移动。每移动一步后，重新确认新的方向，最后不断迭代到达或接近损失函数的最小值。

2.1.4 梯度下降算法的核心逻辑与关键问题

  • 在梯度下降过程中，每一步移动的方向是当前坐标点对应梯度向量的反方向，移动距离为步长与该梯度向量模长的乘积。梯度向量的性质确保沿其反方向、按其大小移动时，能逼近损失函数的最小值。此过程存在两个核心问题：
  1. 如何确定梯度向量的方向和大小？
  2. 如何让坐标点沿梯度向量的反方向移动与梯度向量大小相等的距离？
    许多基于梯度下降算法的改进均围绕上述两个问题展开，以下先解决第一个问题。
  1. 梯度向量的定义与计算
  • 梯度向量是多元函数中各自变量偏导数组成的向量 。以损失函数 L ( w 1 , w 2 , b ) L(w_1, w_2, b) L(w1,w2,b)为例，对其自变量 w 1 , w 2 , b w_1, w_2, b w1,w2,b分别求偏导后，梯度向量为：
    ∇ L ( w 1 , w 2 ) = [ ∂ L ∂ w 1 , ∂ L ∂ w 2 , ∂ L ∂ b ] T \nabla L(w_1, w_2) = \left[ \frac{\partial L}{\partial w_1}, \frac{\partial L}{\partial w_2}, \frac{\partial L}{\partial b} \right]^T ∇L(w1,w2)=[∂w1∂L,∂w2∂L,∂b∂L]T
    也可简写为 grad L ( w 1 , w 2 ) \text{grad}\ L(w_1, w_2) grad L(w1,w2) 或 ∇ L ( w 1 , w 2 ) \nabla L(w_1, w_2) ∇L(w1,w2)。
  1. 向量方向与大小的通用规则
  • 对任意向量（如 ( 1 , 2 ) (1, 2) (1,2)），其方向由元素值决定（从原点指向该点的方向），大小（模长）通过欧几里得范数计算：
    模长 = 1 2 + 2 2 \text{模长} = \sqrt{1^2 + 2^2} 模长=12+22
  • B梯度向量的方向与大小遵循相同逻辑------其元素为各自变量的偏导数，需结合当前坐标点的值计算具体数值。
  • 梯度向量的特性
  1. 唯一性：每个坐标点对应的梯度向量方向和大小是唯一的；坐标点变化时，梯度向量的方向和大小也会随之改变。
  2. 动态更新：每到达新坐标点，读取该点坐标并代入梯度向量表达式，即可得到当前点对应的梯度向量方向和大小。

关键难点

  • 在由损失函数 L ( w ) L(w) L(w)和权重 w w w构成的坐标空间中，只要获得一组坐标值就能求解当前梯度向量。但这一步骤的核心难点在于如何推导梯度向量的表达式------即损失函数对各自变量求偏导后的解析式。

2.2 让坐标点移动（进行迭代）

  • 通过第一步确定大小和方向后，我们思考第二个问题：如何让坐标点沿梯度向量的反方向移动与梯度向量大小相等的距离？
  • 假设现在我们有坐标点 A ( 10 , 7.5 ) A(10, 7.5) A(10,7.5)，向量 g ⃗ \vec{g} g 为 ( 5 , 5 ) (5, 5) (5,5)，其大小为 5 2 5\sqrt{2} 52 。现在我们让点 A A A 向 g ⃗ \vec{g} g 的反方向移动 5 2 5\sqrt{2} 52 的距离。

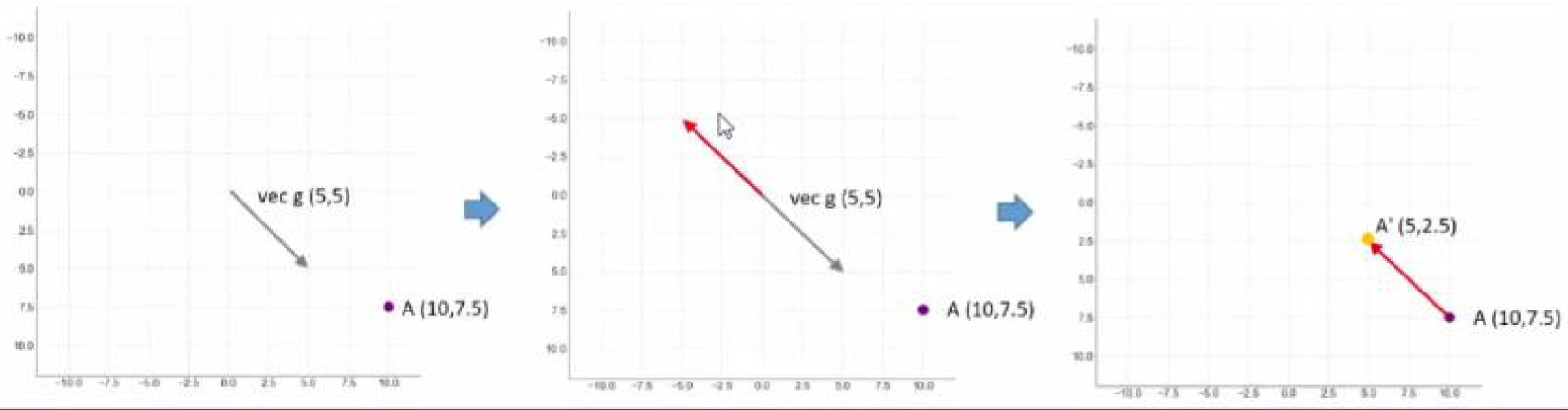
    在梯度下降算法中，坐标点沿梯度反方向移动的过程：
  1. 向量表示与方向确定 ：在坐标系中同时绘制当前点 A A A 及其梯度向量 g ⃗ \vec{g} g 。梯度向量的反方向即为优化方向，用红色箭头标识。
  2. 反方向向量的平移 ：将反方向向量平移，使其起点与 A A A 重合。平移后，该向量的终点即为新点 A ′ A' A′。
  3. 坐标更新规则 ：从 A A A 移动至 A ′ A' A′ 的过程，本质上是沿梯度反方向移动 5 2 5\sqrt{2} 52 单位距离。这一移动导致 A A A 的两个坐标值分别减少 5，从而得到 A ′ A' A′。
  • 该过程体现了梯度下降的核心机制：通过梯度方向指导坐标更新，逐步逼近损失函数的最小值。

2.2.1 梯度下降与权重迭代

  1. 初始点与梯度向量的移动：假设初始点为 ( w 1 ( 0 ) , w 2 ( 0 ) ) (w_{1(0)}, w_{2(0)}) (w1(0),w2(0))，损失函数 L L L 对权重的梯度向量为 ( ∂ L ∂ w 1 , ∂ L ∂ w 2 ) \left(\frac{\partial L}{\partial w_1}, \frac{\partial L}{\partial w_2}\right) (∂w1∂L,∂w2∂L)。坐标点沿梯度反方向移动的更新规则为：
    w 1 ( 1 ) = w 1 ( 0 ) − ∂ L ∂ w 1 w 2 ( 1 ) = w 2 ( 0 ) − ∂ L ∂ w 2 w_{1(1)} = w_{1(0)} - \frac{\partial L}{\partial w_1} \\ w_{2(1)} = w_{2(0)} - \frac{\partial L}{\partial w_2} w1(1)=w1(0)−∂w1∂Lw2(1)=w2(0)−∂w2∂L
  2. 向量形式的迭代公式（第 t t t 步）：将两个权重整合为向量 w \boldsymbol{w} w，用 t t t 表示第 t t t 次迭代，则未引入步长时的迭代公式为：
    w ( t + 1 ) = w ( t ) − ∂ L ∂ w \boldsymbol{w}{(t+1)} = \boldsymbol{w}{(t)} - \frac{\partial L}{\partial \boldsymbol{w}} w(t+1)=w(t)−∂w∂L
  3. 引入学习率（步长 η \eta η）控制移动距离：为控制每次迭代的步长大小，加入学习率 η \eta η（又称"步长"），修正后的迭代公式为：
    w ( t + 1 ) = w ( t ) − η ∂ L ∂ w \boldsymbol{w}{(t+1)} = \boldsymbol{w}{(t)} - \eta \frac{\partial L}{\partial \boldsymbol{w}} w(t+1)=w(t)−η∂w∂L
  • 偏导数的大小影响整体向量的大小，偏导数前的减号影响整体梯度向量的方向。
  • 偏导数 ∂ L ∂ w \frac{\partial L}{\partial \boldsymbol{w}} ∂w∂L决定梯度向量的大小和方向。
  • 学习率 η \eta η 控制每一步沿梯度反方向的移动幅度： η \eta η 越大，迭代速度越快； η \eta η 越小，迭代速度越慢。

2.2.2 jupyter中绘制代码

python 复制代码 
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

# 生成权重网格
w1 = np.arange(-15, 15, 0.05)
w2 = np.arange(-15, 15, 0.05)
w1, w2 = np.meshgrid(w1, w2)

# 定义损失函数（示例：SSE形式）
lossfn = (2 - w1 - w2)**2 + (4 - 3*w1 - w2)**2

# 定义要标记的点
point = (7.5, 10)
w1_point, w2_point = point
loss_point = (2 - w1_point - w2_point)**2 + (4 - 3*w1_point - w2_point)**2

# 计算该点的梯度
grad_w1 = -2 * (2 - w1_point - w2_point) - 6 * (4 - 3*w1_point - w2_point)
grad_w2 = -2 * (2 - w1_point - w2_point) - 2 * (4 - 3*w1_point - w2_point)

# 绘制三维损失曲面
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制表面图
surf = ax.plot_surface(w1, w2, lossfn, cmap='rainbow', alpha=0.7)

# 标记点
ax.scatter([w1_point], [w2_point], [loss_point], color='black', s=100, label='Point (7.5, 10)')

# 绘制梯度向量（在坐标平面上）
ax.quiver(w1_point, w2_point, 0, grad_w1, grad_w2, 0, color='red', length=5, normalize=True, label='Gradient')

# 设置视角（可手动调整）
ax.view_init(elev=30, azim=-20)

# 标签设置
ax.set_xlabel("w1", fontsize=14)
ax.set_ylabel("w2", fontsize=14)
ax.set_zlabel("lossfn", fontsize=14)

# 添加颜色条
fig.colorbar(surf, shrink=0.5, aspect=5)

plt.title("3D Loss Surface with Gradient at (7.5, 10)", fontsize=16)
plt.legend()
plt.tight_layout()
plt.show()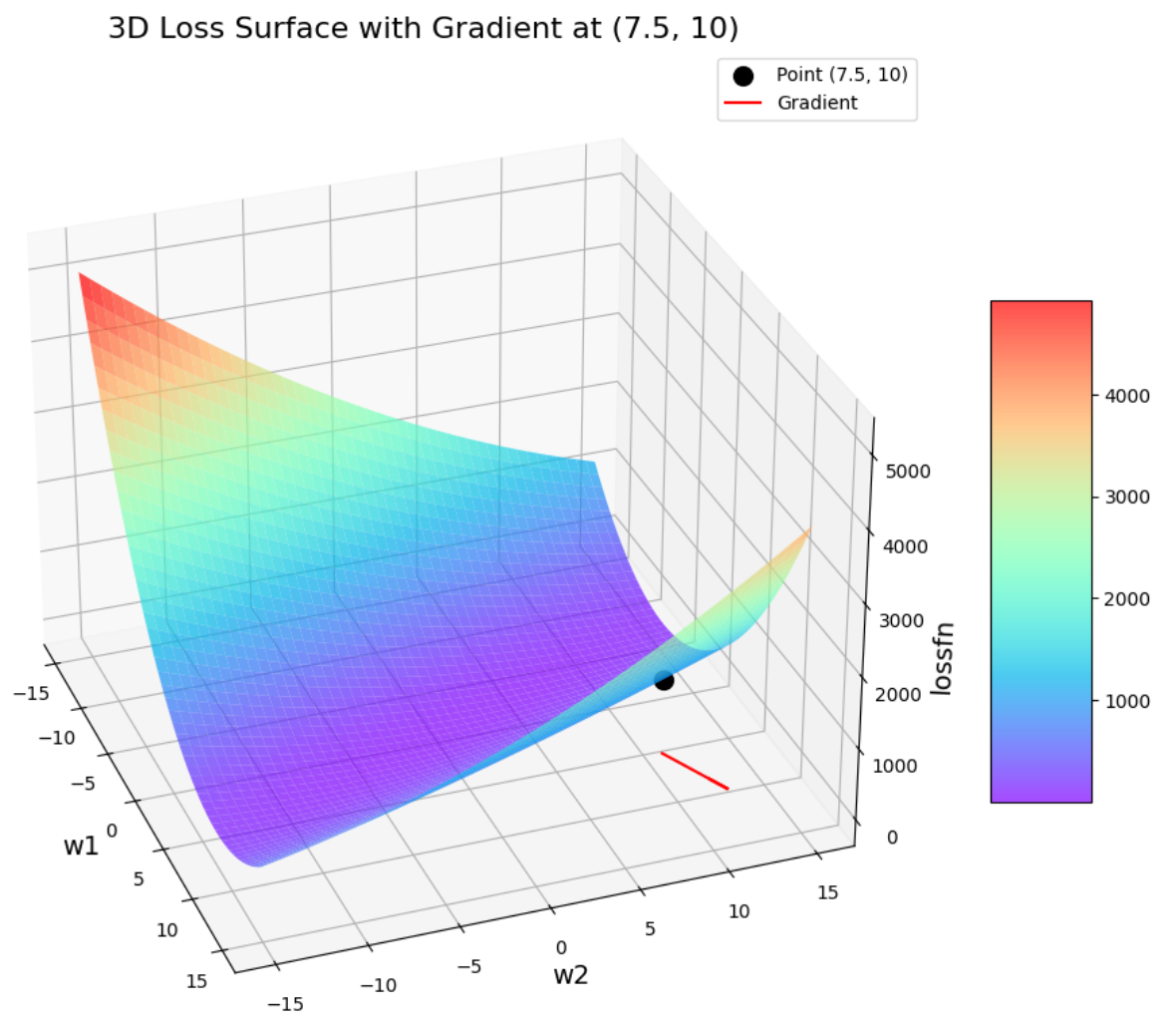

三 找出距离和方向：反向传播

3.1 方向传播的定义与价值

  • 在梯度下降的最初，需要先找出坐标点对应的梯度向量。梯度向量是各个自变量求偏导后的表达式再带入坐标点计算出来的，在这一步骤中，难点在于如何获得梯度向量的表达式一一也损失函数对各个自变量求偏导后的表达式。在单层神经网络，例如逻辑回归（二分类单层神经网络）中，计算如下：
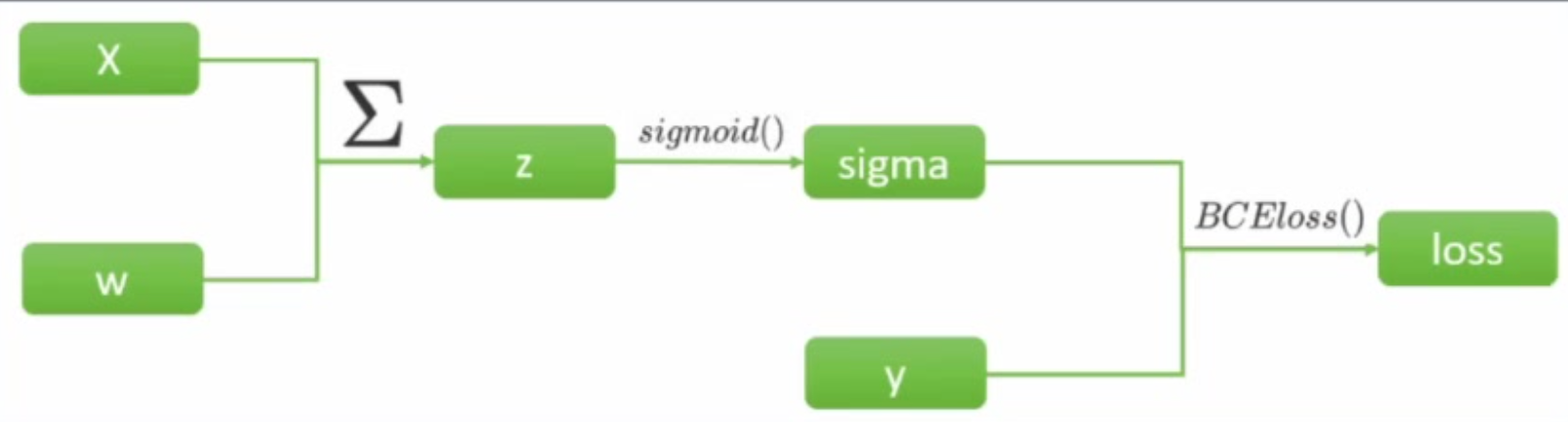
  • BCEloss是二分类交叉熵损失函数。在计算图中，从左向右计算是正向传播，因此进行以此计算后，我们会获得所有节点上的张量的值（z、sigma以及loss）。根据梯度向量的定义，在这个计算过程中，要求的是损失函数对w的导数，所以求导过程需要的链路如下：
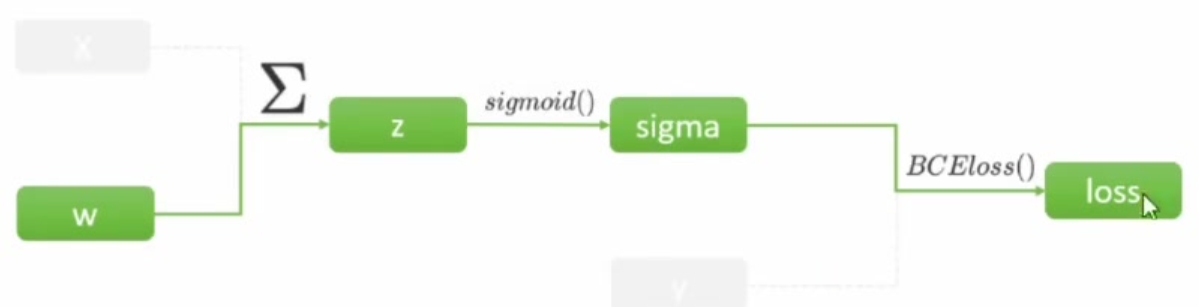
  • 梯度符号（∇）表示对 w w w的导数： ∂ L o s s ∂ w \frac{\partial Loss}{\partial w} ∂w∂Loss
  • 损失函数 L o s s Loss Loss 定义为：
    L o s s = − ∑ i = 1 m ( y i ⋅ ln ⁡ ( σ i ) + ( 1 − y i ) ⋅ ln ⁡ ( 1 − σ i ) ) Loss = -\sum_{i=1}^{m} \left( y_i \cdot \ln(\sigma_i) + (1 - y_i) \cdot \ln(1 - \sigma_i) \right) Loss=−i=1∑m(yi⋅ln(σi)+(1−yi)⋅ln(1−σi))
    进一步展开 σ i \sigma_i σi（sigmoid 函数输出）：
    L o s s = − ∑ i = 1 m ( y i ⋅ ln ⁡ ( 1 1 + e − X i w ) + ( 1 − y i ) ⋅ ln ⁡ ( 1 − 1 1 + e − X i w ) ) Loss = -\sum_{i=1}^{m} \left( y_i \cdot \ln\left( \frac{1}{1 + e^{-X_i w}} \right) + (1 - y_i) \cdot \ln\left( 1 - \frac{1}{1 + e^{-X_i w}} \right) \right) Loss=−i=1∑m(yi⋅ln(1+e−Xiw1)+(1−yi)⋅ln(1−1+e−Xiw1))
  • 以上计算已经够复杂了，更夸张一点，在双层、各层激活函数均为 sigmoid 的二分类神经网络中，正向传播与求导链路的计算流程如下：
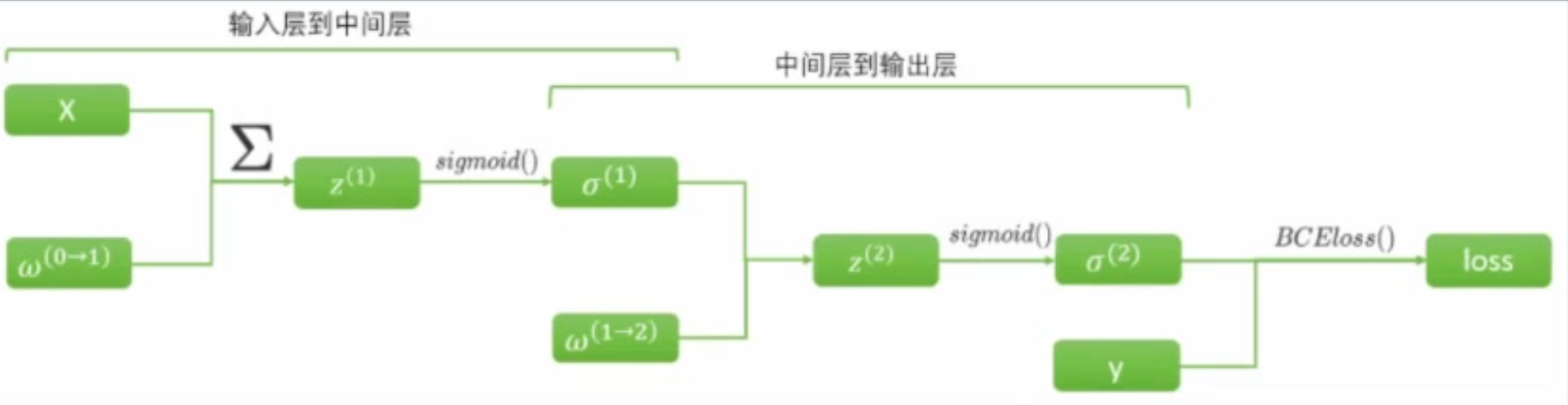
  • 用公式表示对 w ( 1 → 2 ) w^{(1→2)} w(1→2)的求导： ∂ L o s s ∂ w ( 1 → 2 ) \frac{\partial Loss}{\partial w^{(1→2)}} ∂w(1→2)∂Loss
    L o s s = − ∑ i = 1 m ( y i ⋅ ln ⁡ ( σ i ( 2 ) ) + ( 1 − y i ) ⋅ ln ⁡ ( 1 − σ i ( 2 ) ) ) = − ∑ i = 1 m ( y i ⋅ ln ⁡ ( 1 1 + e − σ i ( 1 ) w ( 1 → 2 ) ) + ( 1 − y i ) ⋅ ln ⁡ ( 1 − 1 1 + e − σ i ( 1 ) w ( 1 → 2 ) ) ) \begin{align*} Loss &= -\sum_{i=1}^{m} \left( y_i \cdot \ln(\sigma_i^{(2)}) + (1 - y_i) \cdot \ln(1 - \sigma_i^{(2)}) \right) \\ &= -\sum_{i=1}^{m} \left( y_i \cdot \ln\left( \frac{1}{1 + e^{-\sigma_i^{(1)} w^{(1 \to 2)}}} \right) + (1 - y_i) \cdot \ln\left( 1 - \frac{1}{1 + e^{-\sigma_i^{(1)} w^{(1 \to 2)}}} \right) \right) \end{align*} Loss=−i=1∑m(yi⋅ln(σi(2))+(1−yi)⋅ln(1−σi(2)))=−i=1∑m(yi⋅ln(1+e−σi(1)w(1→2)1)+(1−yi)⋅ln(1−1+e−σi(1)w(1→2)1))
  • 用公式表示对 w ( 0 → 1 ) w^{(0→1)} w(0→1)的求导： ∂ L o s s ∂ w ( 0 → 1 ) \frac{\partial Loss}{\partial w^{(0→1)}} ∂w(0→1)∂Loss
    L o s s = − ∑ i = 1 m ( y i ⋅ ln ⁡ ( σ i ( 2 ) ) + ( 1 − y i ) ⋅ ln ⁡ ( 1 − σ i ( 2 ) ) ) = − ∑ i = 1 m ( y i ⋅ ln ⁡ ( 1 1 + e − 1 1 + e − X i w ( 0 → 1 ) w ( 1 → 2 ) ) + ( 1 − y i ) ⋅ ln ⁡ ( 1 − 1 1 + e − 1 1 + e − X i w ( 0 → 1 ) w ( 1 → 2 ) ) ) \begin{align*} Loss &= -\sum_{i=1}^{m} \left( y_i \cdot \ln(\sigma_i^{(2)}) + (1 - y_i) \cdot \ln(1 - \sigma_i^{(2)}) \right) \\ &= -\sum_{i=1}^{m} \left( y_i \cdot \ln\left( \frac{1}{1 + e^{ -\frac{1}{1 + e^{-X_i w^{(0 \to 1)}} } w^{(1 \to 2)}}} \right) + (1 - y_i) \cdot \ln\left( 1 - \frac{1}{1 + e^{ -\frac{1}{1 + e^{-X_i w^{(0 \to 1)}} } w^{(1 \to 2)}}} \right) \right) \end{align*} Loss=−i=1∑m(yi⋅ln(σi(2))+(1−yi)⋅ln(1−σi(2)))=−i=1∑m(yi⋅ln(1+e−1+e−Xiw(0→1)1w(1→2)1)+(1−yi)⋅ln(1−1+e−1+e−Xiw(0→1)1w(1→2)1))
  • 此等式子，求导何其困难！
  • 神经网络求导的复杂性曾是该领域的一大难题，直到1986年才被有效解决。这一年，Rumelhart、Hinton 和 Williams 提出了反向传播算法（Backpropagation Algorithm，又称 Delta 法则） ，通过巧妙运用链式法则，大幅简化了复杂网络的梯度计算过程。
  • 链式法则：当一个函数是由多个函数嵌套而成，最外层函数向最内层自变量求导的值，等于外层函数对外层自变量求导的值×内层函数对内层自变量求导的值。假设有函数 u = h ( z ) u = h(z) u=h(z)， z = f ( w ) z = f(w) z=f(w)，且两个函数在各自自变量的定义域上都可导，则有
    ∂ u ∂ w = ∂ u ∂ z ⋅ ∂ z ∂ w \frac{\partial u}{\partial w} = \frac{\partial u}{\partial z} \cdot \frac{\partial z}{\partial w} ∂w∂u=∂z∂u⋅∂w∂z

3.1.1 反向传播算法求 w ( 1 → 2 ) w^{(1\to 2)} w(1→2)导数

  • 当函数直接存在复杂的嵌套关系，并且需要从最外层的函数向最内层的自变量导时，链式法则可以让求导过程变得异常简单。以两层二分类网络为例，对 w ( 1 → 2 ) w^{(1→2)} w(1→2)求解：
    ∂ L o s s ∂ w ( 1 → 2 ) = ∂ L ( σ ) ∂ σ ⋅ ∂ σ ( z ) ∂ z ⋅ ∂ z ( w ) ∂ w \begin{align*} \frac{\partial Loss}{\partial w^{(1 \to 2)}} &= \frac{\partial L(\sigma)}{\partial \sigma} \cdot \frac{\partial \sigma(z)}{\partial z} \cdot \frac{\partial z(w)}{\partial w} \\ \end{align*} ∂w(1→2)∂Loss=∂σ∂L(σ)⋅∂z∂σ(z)⋅∂w∂z(w)

∂ L ( σ ) ∂ σ = ∂ ( − ∑ i = 1 m ( y i ⋅ ln ⁡ ( σ i ) + ( 1 − y i ) ⋅ ln ⁡ ( 1 − σ i ) ) ) ∂ σ = ∑ i = 1 m ∂ ( − ( y i ⋅ ln ⁡ ( σ i ) + ( 1 − y i ) ⋅ ln ⁡ ( 1 − σ i ) ) ) ∂ σ = − ∑ i = 1 m ( y ⋅ 1 σ + ( 1 − y ) ⋅ 1 1 − σ ⋅ ( − 1 ) ) = − ∑ i = 1 m ( y σ + y − 1 1 − σ ) = − ∑ i = 1 m ( y − y σ + y σ − σ σ ( 1 − σ ) ) = − ∑ i = 1 m σ − y σ ( 1 − σ ) \begin{align*} \frac{\partial L(\sigma)}{\partial \sigma} &= \frac{\partial \left( -\sum_{i=1}^{m} \left( y_i \cdot \ln(\sigma_i) + (1 - y_i) \cdot \ln(1 - \sigma_i) \right) \right)}{\partial \sigma} \\ &= \sum_{i=1}^{m} \frac{\partial \left( -(y_i \cdot \ln(\sigma_i) + (1 - y_i) \cdot \ln(1 - \sigma_i)) \right)}{\partial \sigma} \\ &= - \sum_{i=1}^{m} (y\cdot \frac{1}{\sigma}+(1-y)\cdot \frac{1}{1-\sigma}\cdot(-1)) \\ &= - \sum_{i=1}^{m} (\frac{y}{\sigma}+ \frac{y-1}{1-\sigma}) \\ &= - \sum_{i=1}^{m}(\frac{y-y\sigma+y\sigma-\sigma}{\sigma(1-\sigma)}) \\ &= - \sum_{i=1}^{m}\frac{\sigma-y}{\sigma(1-\sigma)} \end{align*} ∂σ∂L(σ)=∂σ∂(−∑i=1m(yi⋅ln(σi)+(1−yi)⋅ln(1−σi)))=i=1∑m∂σ∂(−(yi⋅ln(σi)+(1−yi)⋅ln(1−σi)))=−i=1∑m(y⋅σ1+(1−y)⋅1−σ1⋅(−1))=−i=1∑m(σy+1−σy−1)=−i=1∑m(σ(1−σ)y−yσ+yσ−σ)=−i=1∑mσ(1−σ)σ−y

∂ σ ( z ) ∂ z = ∂ ( 1 1 + e − z ) ∂ z = ∂ ( ( 1 + e − z ) − 1 ) ∂ z = − 1 ⋅ ( 1 + e − z ) − 2 ⋅ e − z ⋅ ( − 1 ) = e − z ( 1 + e − z ) 2 = 1 + e − z − 1 ( 1 + e − z ) 2 = 1 + e − z ( 1 + e − z ) 2 − 1 ( 1 + e − z ) 2 = 1 1 + e − z − 1 ( 1 + e − z ) 2 = 1 1 + e − z ( 1 − 1 1 + e − z ) = σ ( z ) ⋅ ( 1 − σ ( z ) ) \begin{align*} \frac{\partial \sigma(z)}{\partial z} &= \frac{\partial \left( \frac{1}{1 + e^{-z}} \right)}{\partial z} \\ &= \frac{\partial \left( (1 + e^{-z})^{-1} \right)}{\partial z} \\ &= -1 \cdot (1 + e^{-z})^{-2} \cdot e^{-z} \cdot (-1) \\ &= \frac{e^{-z}}{(1 + e^{-z})^2} \\ &= \frac{1 + e^{-z} - 1}{(1 + e^{-z})^2} \\ &= \frac{1 + e^{-z}}{(1 + e^{-z})^2} - \frac{1}{(1 + e^{-z})^2} \\ &= \frac{1}{1 + e^{-z}} - \frac{1}{(1 + e^{-z})^2} \\ &= \frac{1}{1 + e^{-z}} \left( 1 - \frac{1}{1 + e^{-z}} \right) \\ &= \sigma(z) \cdot (1 - \sigma(z)) \end{align*} ∂z∂σ(z)=∂z∂(1+e−z1)=∂z∂((1+e−z)−1)=−1⋅(1+e−z)−2⋅e−z⋅(−1)=(1+e−z)2e−z=(1+e−z)21+e−z−1=(1+e−z)21+e−z−(1+e−z)21=1+e−z1−(1+e−z)21=1+e−z1(1−1+e−z1)=σ(z)⋅(1−σ(z))

∂ z ( w ) ∂ w = ∂ ( 1 ) w ∂ w = ∂ ( 1 ) \begin{align*} \frac{\partial z(w)}{\partial w}& = \frac{\partial^{(1)} w}{\partial w} \\ &= \partial^{(1)} \end{align*} ∂w∂z(w)=∂w∂(1)w=∂(1)

  • 三项整合后，可以发现最终的表达式非常简单，其中的数据都是我们在正向传播过程中已经计算出来的节点上的张量。
    ∂ L o s s ∂ w ( 1 → 2 ) = ∂ L ( σ ) ∂ σ ⋅ ∂ σ ( 2 ) ( z ) ∂ z ⋅ ∂ z ( w ) ∂ w = σ ( 2 ) − y σ ( 2 ) ( 1 − σ ( 2 ) ) ⋅ σ ( 2 ) ( 1 − σ ( 2 ) ) ⋅ σ ( 1 ) = σ ( 1 ) ( σ ( 2 ) − y ) \begin{align*} \frac{\partial Loss}{\partial w^{(1 \to 2)}} &= \frac{\partial L(\sigma)}{\partial \sigma} \cdot \frac{\partial \sigma^{(2)}(z)}{\partial z} \cdot \frac{\partial z(w)}{\partial w} \\ &= \frac{\sigma^{(2)} - y}{\sigma^{(2)}(1 - \sigma^{(2)})} \cdot \sigma^{(2)}(1 - \sigma^{(2)}) \cdot \sigma^{(1)} \\ &= \sigma^{(1)} (\sigma^{(2)} - y) \end{align*} ∂w(1→2)∂Loss=∂σ∂L(σ)⋅∂z∂σ(2)(z)⋅∂w∂z(w)=σ(2)(1−σ(2))σ(2)−y⋅σ(2)(1−σ(2))⋅σ(1)=σ(1)(σ(2)−y)

3.1.2 反向传播算法求 w ( 0 → 1 ) w^{(0\to1)} w(0→1)导数

  • 由前面的计算可知
    ∂ L ( σ ) ∂ σ ( 2 ) ⋅ ∂ σ ( 2 ) ( z ( 2 ) ) ∂ z ( 2 ) = ( σ ( 2 ) − y ) \frac{\partial L(\sigma)}{\partial \sigma^{(2)}} \cdot \frac{\partial \sigma^{(2)}(z^{(2)})}{\partial z^{(2)}} = (\sigma^{(2)} - y) ∂σ(2)∂L(σ)⋅∂z(2)∂σ(2)(z(2))=(σ(2)−y)

∂ L o s s ∂ w ( 0 → 1 ) = ∂ L ( σ ) ∂ σ ( 2 ) ⋅ ∂ σ ( 2 ) ( z ( 2 ) ) ∂ z ( 2 ) ⋅ ∂ z ( 2 ) ( σ ( 1 ) ) ∂ σ ( 1 ) ⋅ ∂ σ ( 1 ) ( z ( 1 ) ) ∂ z ( 1 ) ⋅ ∂ z ( 1 ) ( w ( 0 → 1 ) ) ∂ w ( 0 → 1 ) = ( σ ( 2 ) − y ) ⋅ ∂ z ( 2 ) ( σ ( 1 ) ) ∂ σ ( 1 ) ⋅ ∂ σ ( 1 ) ( z ( 1 ) ) ∂ z ( 1 ) ⋅ ∂ z ( 1 ) ( w ( 0 → 1 ) ) ∂ w ( 0 → 1 ) = ( σ ( 2 ) − y ) ⋅ w ( 1 → 2 ) ⋅ σ ( 1 ) ( 1 − σ ( 1 ) ) ⋅ X \begin{align*} \frac{\partial Loss}{\partial w^{(0 \to 1)}} &= \frac{\partial L(\sigma)}{\partial \sigma^{(2)}} \cdot \frac{\partial \sigma^{(2)}(z^{(2)})}{\partial z^{(2)}} \cdot \frac{\partial z^{(2)}(\sigma^{(1)})}{\partial \sigma^{(1)}} \cdot \frac{\partial \sigma^{(1)}(z^{(1)})}{\partial z^{(1)}} \cdot \frac{\partial z^{(1)}(w^{(0 \to 1)})}{\partial w^{(0 \to 1)}} \\ &= (\sigma^{(2)} - y) \cdot \frac{\partial z^{(2)}(\sigma^{(1)})}{\partial \sigma^{(1)}} \cdot \frac{\partial \sigma^{(1)}(z^{(1)})}{\partial z^{(1)}} \cdot \frac{\partial z^{(1)}(w^{(0 \to 1)})}{\partial w^{(0 \to 1)}} \\ &= (\sigma^{(2)} - y) \cdot w^{(1\to 2)} \cdot \sigma^{(1)}(1-\sigma^{(1)}) \cdot X \\ \end{align*} ∂w(0→1)∂Loss=∂σ(2)∂L(σ)⋅∂z(2)∂σ(2)(z(2))⋅∂σ(1)∂z(2)(σ(1))⋅∂z(1)∂σ(1)(z(1))⋅∂w(0→1)∂z(1)(w(0→1))=(σ(2)−y)⋅∂σ(1)∂z(2)(σ(1))⋅∂z(1)∂σ(1)(z(1))⋅∂w(0→1)∂z(1)(w(0→1))=(σ(2)−y)⋅w(1→2)⋅σ(1)(1−σ(1))⋅X

  • 至此，我们可以发现表达式中需要的全部张量，都是我们在正向传播中已经计算出来存储好的，因此在进行反向传播时，可以节省大量时间，这种从不断使用正向传播中的元素对梯度向量进行计算的方式，就是反向传播。

3.2 PyTorch实现反向传播

  • 在梯度下降中，需要不断更新梯度，计算量巨大。PyTorch可以帮助自动计算梯度，只需要提取梯度向量的值进行迭代即可。PyTorch提供两种方式实现梯度计算。一种是使用 A u t o G r a d AutoGrad AutoGrad，另外一种是使用 t o r c h . a u t o g r a d . g r a d ( ) torch.autograd.grad() torch.autograd.grad()函数计算某个具体点/某个变量的导数。
python 复制代码 
import torch
x = torch.tensor(1., requires_grad=True)
y = x ** 2
torch.autograd.grad(y, x)
python 复制代码 
import torch
x = torch.tensor(1., requires_grad=True)
z = x ** 2
y = torch.tensor(2, requires_grad=True, dtype=torch.float32)
sigma = torch.sigmoid(z)
loss = -(y*torch.log(sigma)+(1-y)*torch.log(1-sigma))
torch.autograd.grad(loss, y)
python 复制代码 
# -*- coding: utf-8 -*-
"""
该脚本演示了一个使用 PyTorch 构建的前馈神经网络（Feed-Forward Neural Network），
用于一个三分类任务。代码涵盖了数据准备、模型定义、前向传播、损失计算、
反向传播以及梯度检查等一个完整的训练步骤所包含的核心环节。
"""

# 导入 PyTorch 的核心库
import torch
# 导入 PyTorch 中的神经网络模块，用于构建网络层
import torch.nn as nn
# 导入 PyTorch 中的函数式接口，包含激活函数等
from torch.nn import functional as F

# --- 1. 数据准备与预处理 ---

# 设置随机种子，确保每次运行代码时，PyTorch 生成的随机数是相同的。
# 这对于实验的可复现性至关重要，可以保证在相同参数下得到相同的结果。
torch.manual_seed(520)

# 创建一个特征矩阵 X，作为模型的输入数据。
# torch.rand() 生成一个 [0, 1) 之间均匀分布的随机张量。
# (500, 20) 表示有 500 个样本，每个样本有 20 个特征。
# dtype=torch.float 指定数据类型为 32 位浮点数，这是神经网络计算的常用类型。
X = torch.rand((500, 20), dtype=torch.float)

# 创建一个标签向量 y，作为模型的目标输出。
# torch.randint() 生成一个指定范围内的随机整数张量。
# low=0, high=3 表示生成的整数在 [0, 3) 范围内，即 0, 1, 2。
# 这代表这是一个三分类问题，每个样本的标签是这三类之一。
# size=(500,) 表示有 500 个样本，与 X 的样本数量一一对应。
# dtype=torch.float32 指定数据类型为 32 位浮点数。注意：虽然标签是整数，
# 但有时在计算中会先以浮点数形式存在，不过在送入损失函数时需要转换为长整型。
y = torch.randint(low=0, high=3, size=(500,), dtype=torch.float32)

# --- 2. 定义模型超参数 ---

# 获取输入特征的数量。
# X.shape[1] 是特征矩阵 X 的列数，即每个样本的特征维度。
# 这个值将作为神经网络输入层的大小。
input_ = X.shape[1]  # input_ 的值为 20

# 获取输出类别的数量。
# y.unique() 找出 y 中所有不重复的标签值（例如 tensor([0., 1., 2.])）。
# len() 计算不同类别的总数。
# 这个值将作为神经网络输出层的大小（即每个类别的得分/概率）。
output_ = len(y.unique()) # output_ 的值为 3


# --- 3. 构建神经网络模型 ---

# 通过继承 nn.Module 来定义我们自己的神经网络模型。
# nn.Module 是所有 PyTorch 模型的基类，提供了很多有用的功能，如参数管理、设备迁移等。
class Model(nn.Module):
    """
    一个包含两个隐藏层的前馈神经网络。
    结构: 输入层 -> 隐藏层1 (ReLU激活) -> 隐藏层2 (Sigmoid激活) -> 输出层
    """
    # 定义类的构造函数（初始化方法），用于创建模型的各个层。
    # in_features: 输入特征的数量，默认为40。
    # out_features: 输出类别的数量，默认为2。
    def __init__(self, in_features=40, out_features=2):
        # 调用父类 nn.Module 的构造函数。这是必须的步骤，用于正确初始化基类。
        super().__init__()

        # 定义第一个全连接层（线性层）。
        # nn.Linear(in_features, out_features, bias)
        # in_features: 该层的输入神经元数量。
        # out_features: 该层的输出神经元数量。
        # bias=False: 表示该层不使用偏置项。
        # 这一层将输入的 in_features 个特征映射到 13 个神经元。
        self.linear1 = nn.Linear(in_features, 13, bias=False)
        # 注意：这里的变量名 "liner1" 是一个拼写错误，应该是 "linear1"。
        # 但为了与原代码保持一致，我们保留此名称。在实际项目中应避免此类错误。

        # 定义第二个全连接层。
        # 它接收前一层的 13 个输出，并将其映射到 8 个神经元。
        self.linear2 = nn.Linear(13, 8, bias=False)

        # 定义输出层。
        # 它接收前一层的 8 个输出，并将其映射到最终的 out_features 个类别得分。
        # bias=True: 表示该层使用偏置项，这是默认设置。
        self.output = nn.Linear(8, out_features, bias=True)

    # 定义前向传播过程。
    # 这个方法描述了数据如何流经网络的各个层。
    # x: 输入到模型的张量数据。
    def forward(self, x):
        # 将输入 x 通过第一个线性层，然后应用 ReLU 激活函数。
        # ReLU (Rectified Linear Unit) 是一种常用的激活函数，公式为 f(x) = max(0, x)。
        # 它引入了非线性，使得网络能够学习更复杂的模式。
        # 【代码潜在问题】：这里使用了全局变量 X 而不是方法参数 x。
        # 正确的写法应该是: sigma1 = torch.relu(self.liner1(x))
        # 当前的写法意味着无论输入什么，模型都只会使用最开始定义的 X 数据，
        # 这会导致模型无法处理新的输入，是严重的逻辑错误。
        sigma1 = torch.relu(self.linear1(x))

        # 将第一层的输出 sigma1 通过第二个线性层，然后应用 Sigmoid 激活函数。
        # Sigmoid 函数将输出压缩到 (0, 1) 区间，可以看作是一种概率或置信度。
        # 在隐藏层中使用 Sigmoid 有时可能导致梯度消失问题，但在这里用于演示。
        sigma2 = torch.sigmoid(self.linear2(sigma1))

        # 将第二层的输出 sigma2 通过输出层，得到最终的预测结果 z_hat。
        # z_hat 通常被称为 "logits"，即每个类别的原始得分，尚未经过 Softmax 转换为概率。
        # nn.CrossEntropyLoss 损失函数在内部会自动处理 logits，所以这里不需要手动加 Softmax。
        z_hat = self.output(sigma2)
        
        # 返回前向传播的最终结果。
        return z_hat

# --- 4. 实例化模型并进行前向传播 ---

# 再次设置随机种子，确保模型初始化的权重是可复现的。
# 这与之前的数据生成种子是独立的，专门用于控制模型参数的初始化。
torch.manual_seed(520)

# 创建 Model 类的一个实例（对象）。
# 将我们之前计算好的输入特征数和输出类别数传入构造函数。
net = Model(in_features=input_, out_features=output_)

# 调用模型实例的 forward() 方法，将数据 X 输入网络，进行一次前向传播。
# 由于 Model 类继承了 nn.Module，我们也可以直接使用 net(X) 来调用 forward() 方法。
# z_hat 是模型的输出，形状为 (500, 3)，代表 500 个样本在 3 个类别上的得分。
z_hat = net.forward(X)


# --- 5. 定义损失函数并计算损失 ---

# 定义损失函数。
# 对于多分类问题，交叉熵损失是标准选择。
# nn.CrossEntropyLoss 结合了 LogSoftmax 和 NLLLoss (Negative Log Likelihood Loss) 的功能。
# 它的输入是模型的原始输出（logits）和真实的类别标签。
# 它要求：
# 1. 模型输出 的形状是
# 2. 真实标签 的形状是，且数据类型为 torch.long。
criterion = nn.CrossEntropyLoss()

# 计算损失值。
# 将模型的预测 z_hat 和真实标签 y 传入损失函数。
# 【关键点】：y.long() 将标签 y 的数据类型从 torch.float32 转换为 torch.long。
# 这是 CrossEntropyLoss 的硬性要求，因为它需要整数形式的类别索引。
# loss 是一个标量张量（0维张量），表示当前模型预测与真实标签之间的差距。
loss = criterion(z_hat, y.long())


# --- 6. 反向传播与梯度计算 ---

# 执行反向传播，计算损失函数相对于模型中所有可训练参数的梯度。
# PyTorch 会自动构建一个计算图，loss.backward() 会沿着这个图从 loss 开始，
# 使用链式法则计算所有叶子节点（即模型参数，如权重和偏置）的梯度。
# 计算出的梯度会累积在每个参数的 .grad 属性中。
# retain_graph=True: 表示在反向传播后保留计算图。
# 通常情况下，一次反向传播后计算图会被释放。如果需要在同一个计算图上多次调用 backward()（例如在某些高级训练技巧中），
# 就需要设置此参数为 True。对于简单的单步 backward，此参数可以省略。
loss.backward(retain_graph=True)

# 访问并查看模型第一个线性层（liner1）权重的梯度。
# net.liner1.weight 是一个包含该层权重的张量。
# .grad 属性存储了在 backward() 过程中计算出的梯度。
# 如果一个参数没有参与计算，或者没有调用 backward()，它的 .grad 属性会是 None。
# 在调用优化器的 step() 方法更新参数后，这些梯度通常会被清零（通过 optimizer.zero_grad()）。
# 这里我们只是检查梯度是否被正确计算。
net.linear1.weight.grad

四 移动坐标点

4.1 移动第一步

  • 权重迭代公式：
    w ( t + 1 ) = w ( t ) − η ∂ L ( w ) ∂ w w_{(t+1)}=w_{(t)}- \eta \frac{\partial L(w)}{\partial w} w(t+1)=w(t)−η∂w∂L(w)
  • 偏导数部分通过反向传播计算已经获得， η \eta η称为步长，一般是人为设置，通常为 0.01 0.05 0.01~0.05 0.01 0.05。
python 复制代码 
import torch
import torch.nn as nn
from torch.nn import functional as F

# --- 1. 数据准备与预处理 ---
# 设置随机种子，确保每次运行代码时，PyTorch 生成的随机数是相同的。
torch.manual_seed(520)

# 创建一个特征矩阵 X，作为模型的输入数据。
X = torch.rand((500, 20), dtype=torch.float)

# 创建一个标签向量 y，作为模型的目标输出。
y = torch.randint(low=0, high=3, size=(500,), dtype=torch.float32)

# --- 2. 定义模型超参数 ---
input_ = X.shape[1]  # input_ 的值为 20
output_ = len(y.unique()) # output_ 的值为 3


# --- 3. 构建神经网络模型 ---

class Model(nn.Module):
    def __init__(self, in_features=40, out_features=2):
        # 调用父类 nn.Module 的构造函数。这是必须的步骤，用于正确初始化基类。
        super().__init__()

        self.linear1 = nn.Linear(in_features, 13, bias=False)
        # 注意：这里的变量名 "liner1" 是一个拼写错误，应该是 "linear1"。
        # 但为了与原代码保持一致，我们保留此名称。在实际项目中应避免此类错误。


        self.linear2 = nn.Linear(13, 8, bias=False)

        self.output = nn.Linear(8, out_features, bias=True)


    def forward(self, x):
        sigma1 = torch.relu(self.linear1(x))
        sigma2 = torch.sigmoid(self.linear2(sigma1))
        z_hat = self.output(sigma2)
        
        return z_hat

# --- 4. 实例化模型并进行前向传播 ---
torch.manual_seed(520)
net = Model(in_features=input_, out_features=output_)
z_hat = net.forward(X)

# --- 5. 定义损失函数并计算损失 ---
criterion = nn.CrossEntropyLoss()
loss = criterion(z_hat, y.long())


# --- 6. 反向传播与梯度计算 ---
loss.backward(retain_graph=True)

net.linear1.weight.grad

lr = 0.01
w = net.linear1.weight.data
d_w = net.linear1.weight.grad
w -= lr*d_w
print(w)

4.2 从1到N：动量法

  • 要理解动量法（Momentum），需理解梯度下降的局限：传统梯度下降中，起始点无法利用历史移动方向信息，每次仅按当前梯度反方向小步更新，效率低且易陷入局部最优。
  • 动量法的核心改进是引入"动量"概念 ：通过加权融合"上一步梯度的反方向"（权重为动量参数γ）与"当前梯度反方向"（权重为学习率η），得到真实下降方向 v v v，再沿该方向更新坐标。
    其中， v prev v_{\text{prev}} vprev是上一步的动量向量， ∇ f ( x ) \nabla f(x) ∇f(x) 是当前梯度。
    这种设计让优化过程具备"惯性"：若历史与当前方向一致，可大步加速；若方向相反，则小步调整，从而提升收敛速度与稳定性。
  • 可以理解为让上一步的梯度向量(反向)与现在这一点的梯度向量(反方向)以加权求和，求解出受到上一步大小和方向影响的真实下降方向，再让坐标点向真实下降方向移动。
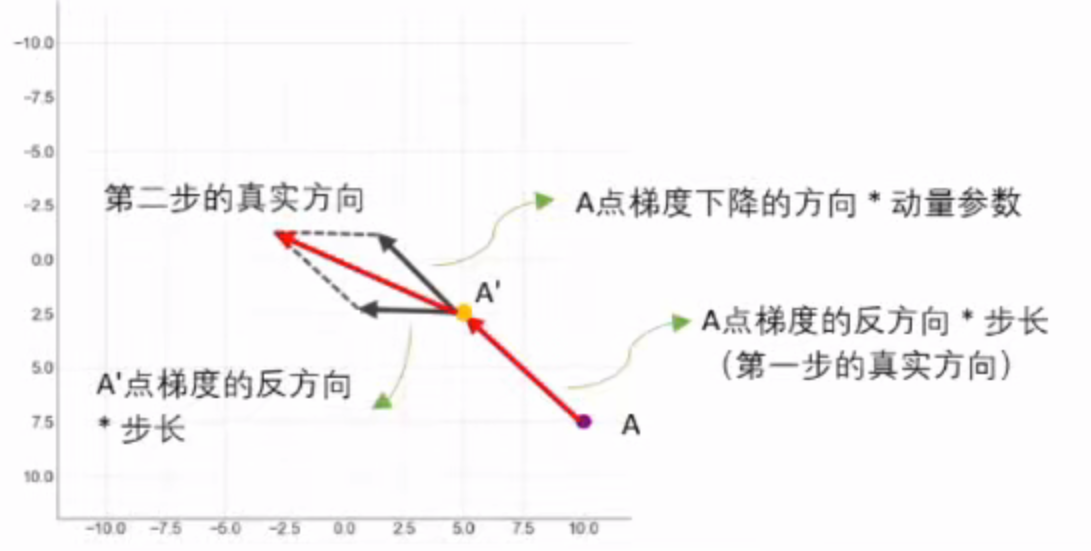
  • 其中对上一步的梯度向量加上的权重被称为动量参数，对这一点的梯度向量加上的权重就是步长，真实移动的向量为 v v v，被称为动量。

v ( t ) = γ v t-1 − η L ∂ w w ( t + 1 ) = w ( t ) + v ( t ) v_{(t)} = \gamma v_{\text{t-1}} - \eta \frac{L}{\partial w} \\ w_{(t+1)} = w_{(t)}+v_{(t)} v(t)=γvt-1−η∂wLw(t+1)=w(t)+v(t)

第一步无历史梯度方向，故真实方向为起始点梯度反方向 v 0 = 0 v_0 = 0 v0=0, v ( t − 1 ) v_{(t-1)} v(t−1) 表示之前所有步骤累积的动量和（即上一步真实方向）。此时梯度下降方向具"惯性"，受历史累计动量影响：新坐标点梯度反方向与历史累计动量方向一致时，历史累计动量增大实际方向步子；不一致时，减小实际方向步子。

python 复制代码 
import torch
import torch.nn as nn
from torch.nn import functional as F

# --- 1. 数据准备与预处理 ---
# 设置随机种子，确保每次运行代码时，PyTorch 生成的随机数是相同的。
torch.manual_seed(520)

# 创建一个特征矩阵 X，作为模型的输入数据。
X = torch.rand((500, 20), dtype=torch.float)

# 创建一个标签向量 y，作为模型的目标输出。
y = torch.randint(low=0, high=3, size=(500,), dtype=torch.float32)

# --- 2. 定义模型超参数 ---
input_ = X.shape[1]  # input_ 的值为 20
output_ = len(y.unique()) # output_ 的值为 3


# --- 3. 构建神经网络模型 ---

class Model(nn.Module):
    def __init__(self, in_features=40, out_features=2):
        # 调用父类 nn.Module 的构造函数。这是必须的步骤，用于正确初始化基类。
        super().__init__()

        self.linear1 = nn.Linear(in_features, 13, bias=False)
        # 注意：这里的变量名 "liner1" 是一个拼写错误，应该是 "linear1"。
        # 但为了与原代码保持一致，我们保留此名称。在实际项目中应避免此类错误。


        self.linear2 = nn.Linear(13, 8, bias=False)

        self.output = nn.Linear(8, out_features, bias=True)


    def forward(self, x):
        sigma1 = torch.relu(self.linear1(x))
        sigma2 = torch.sigmoid(self.linear2(sigma1))
        z_hat = self.output(sigma2)
        
        return z_hat

# --- 4. 实例化模型并进行前向传播 ---
torch.manual_seed(520)
net = Model(in_features=input_, out_features=output_)
z_hat = net.forward(X)

# --- 5. 定义损失函数并计算损失 ---
criterion = nn.CrossEntropyLoss()
loss = criterion(z_hat, y.long())

# --- 6. 反向传播与梯度计算 ---
loss.backward(retain_graph=True)  # 计算损失函数对各参数的梯度，并保留计算图以便后续多次反向传播

net.linear1.weight.grad  # 获取网络中 linear1 层权重参数的梯度值（未赋值，仅用于查看）

lr = 0.01  # 初始化学习率，控制每次更新的步长
gamma = 0.9  # 初始化动量参数，用于控制历史动量的影响程度
w = net.linear1.weight.data  # 获取 linear1 层权重的当前值（数据部分，不涉及梯度）
d_w = net.linear1.weight.grad  # 获取 linear1 层权重的梯度值（用于更新）
v = torch.zeros(d_w.shape[0], d_w.shape[1])  # 初始化动量向量 v，形状与权重梯度相同，初始为全零

v = gamma * v - lr * d_w  # 更新动量向量：结合历史动量（gamma*v）和当前梯度（-lr*d_w）
w += v  # 使用动量向量 v 更新权重值
print(w)  # 打印更新后的权重值

4.3 实现带动量的梯度下降

  • 在PyTorch库的架构中，拥有专门实现优化算法的模块torch.optim。我们在之前的课程中所说的迭代流程，都可以通过torch.optim模块来简单地实现。
python 复制代码 
import torch
import torch.nn as nn
import torch.optim as optim
from torch.nn import functional as F

# --- 1. 数据准备与预处理 ---
# 设置随机种子，确保每次运行代码时，PyTorch 生成的随机数是相同的。
torch.manual_seed(520)

# 创建一个特征矩阵 X，作为模型的输入数据。
X = torch.rand((500, 20), dtype=torch.float)

# 创建一个标签向量 y，作为模型的目标输出。
y = torch.randint(low=0, high=3, size=(500,), dtype=torch.float32)

lr = 0.01  # 初始化学习率，控制每次更新的步长
gamma = 0.9  # 初始化动量参数，用于控制历史动量的影响程度

# --- 2. 定义模型超参数 ---
input_ = X.shape[1]  # input_ 的值为 20
output_ = len(y.unique()) # output_ 的值为 3


# --- 3. 构建神经网络模型 ---

class Model(nn.Module):
    def __init__(self, in_features=40, out_features=2):
        # 调用父类 nn.Module 的构造函数。这是必须的步骤，用于正确初始化基类。
        super().__init__()

        self.linear1 = nn.Linear(in_features, 13, bias=False)
        # 注意：这里的变量名 "liner1" 是一个拼写错误，应该是 "linear1"。
        # 但为了与原代码保持一致，我们保留此名称。在实际项目中应避免此类错误。


        self.linear2 = nn.Linear(13, 8, bias=False)

        self.output = nn.Linear(8, out_features, bias=True)


    def forward(self, x):
        sigma1 = torch.relu(self.linear1(x))
        sigma2 = torch.sigmoid(self.linear2(sigma1))
        z_hat = self.output(sigma2)
        
        return z_hat

# --- 4. 定义损失函数和优化算法---
criterion = nn.CrossEntropyLoss()

opt = optim.SGD(
    net.parameters(),
    lr=lr,
    momentum=gamma
)

# --- 5. 实例化模型并进行前向传播 ---
torch.manual_seed(520)

net = Model(in_features=input_, out_features=output_)
z_hat = net.forward(X)

# --- 6. 反向传播 ---
loss = criterion(z_hat, y.reshape(500,).long())
loss.backward()  # 计算损失函数对各参数的梯度，并保留计算图以便后续多次反向传播
opt.step()  # 更新权重
opt.zero_grad()  # 清除梯度
print(loss)

五 开始迭代

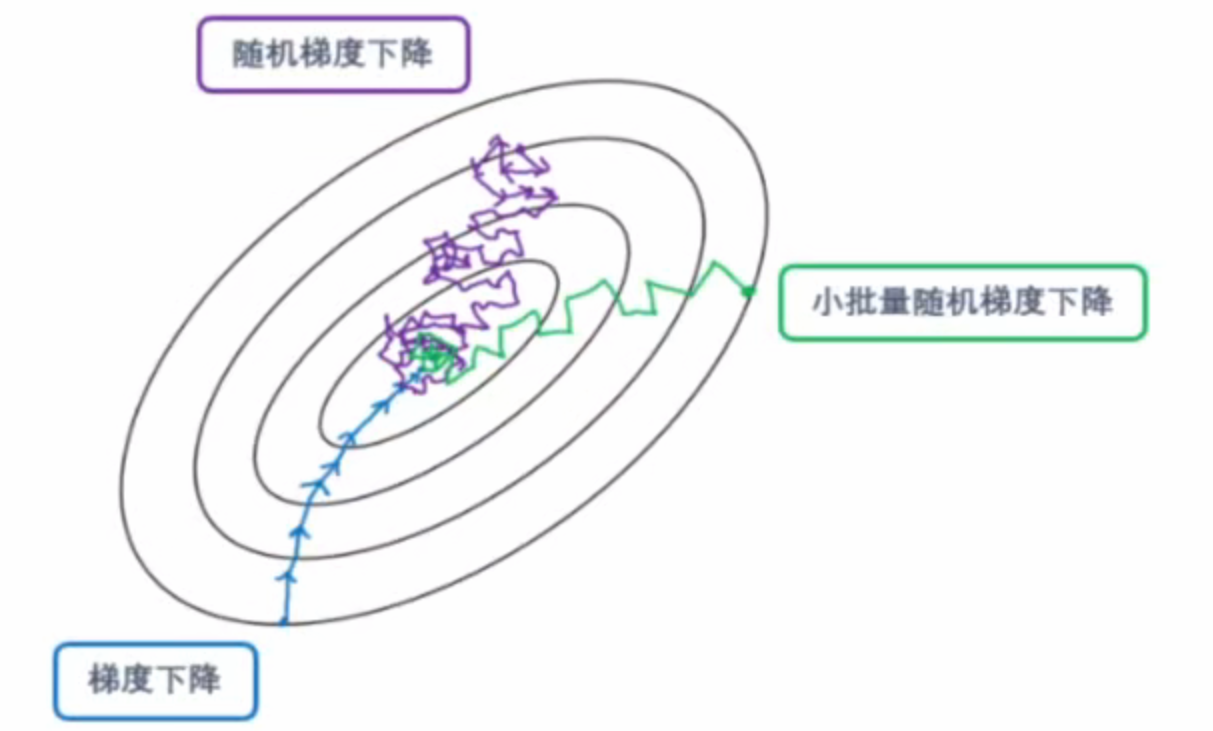
  • 深度学习中，神经网络训练对象多为图像、文本等非结构化高维数据 （如 MNIST 训练集规模达 (60000 \times 784)，远超机器学习入门级数据鸢尾花的 (150 \times 4)）。若每轮迭代使用全部数据计算梯度，将因样本量过大导致计算开销剧增 。尽管 PyTorch 支持海量数据处理，但仍需优化数据使用方式------因此引入小批量随机梯度下降（mini-batch SGD） ，以平衡计算效率与梯度估计精度。

5.1 mSGD下降中的 batch_size 与 epochs

5.1.1 batch_size（批量大小）

batch_size 指每次梯度更新所使用的样本数量。它直接影响训练效率和模型收敛性：

  • 大 batch_size ：
    • 梯度估计更稳定，接近真实梯度方向；
    • 计算效率高，适合 GPU 并行加速；
    • 但内存占用大，且可能陷入局部最优。
  • 小 batch_size ：
    • 引入噪声，增强泛化能力，有助于跳出局部最优；
    • 内存占用小，适合资源受限环境；
    • 但训练时间延长，收敛波动较大。

5.1.2 epochs（训练轮数）

epoch 指整个训练集被完整遍历一次的次数。它控制模型学习数据的充分程度：

  • epoch 过少：模型未充分学习数据特征，欠拟合风险高；
  • epoch 过多：模型可能过度拟合训练数据，泛化能力下降。

5.2 二者关系

  • 总迭代次数 = epochs × (样本总数 / batch_size) 例如：1000 样本，batch_size=100，则每 epoch 迭代 10 次。
  • 实际训练中，需结合任务复杂度、硬件资源和模型性能，动态调整 batch_size 和 epochs 以平衡效率与效果。

六 完整流程体验

  • 在MINST-FASHION数据集上，使用小批量梯度下降进行迭代，实现一个完整的训练流程。
  • PyTorch自带数据集相关情况

成熟AI领域 计算机视觉
torchvision 自然语言处理
torchtext 语音处理
torchaudio CV常用数据
torchvision.datasets CV常用模型
torchvision.models 图像数据的预处理工具
torchvision.transforms 文字数据的数据预处理
torchtext.data NLP领域的常用数据集
torchtext.datasets 语音领域的常用数据集
torchaudio.datasets 语音领域的预处理工具
torchaudio.transforms 语音领域的常用模型
torchaudio.models 语音领域的常用函数
torchaudio.functional

  • Fashion-MNIST数据集包含了10个类别的图像，分别是：t-shirt（T恤），trouser（牛仔裤），pullover（套衫），dress（裙子），coat（外套），sandal（凉鞋），shirt（衬衫），sneaker（运动鞋），bag（包），ankle boot（短靴）。
python 复制代码 
import torch
from torch import nn, optim
from torch.nn import functional as F
from torch.utils.data import TensorDataset, DataLoader

# 确定数据、确定优先需要设置的值
lr = 0.15
gamma = 0
epochs = 10
bs = 128

import torchvision
import torchvision.transforms as transforms
mnist = torchvision.datasets.FashionMNIST(
    root="./data",
    download=True,
    train=True,
    transform=transforms.ToTensor()
)  # 实例化数据

mnist.targets.unique()  # 最终10个类别
mnist.classes  # 类别名称
import matplotlib.pyplot as plt
import numpy
plt.imshow(mnist[0][0].view(28, 28).numpy())
  • 基本流程如下：
  1. 设置初始权重 w 0 w_0 w0，步长lr，动量值gamma，迭代次数epochs，batch_size等信息。
  2. 导入数据，将数据切分为batches
  3. 定义神经网络架构
  4. 定义损失函数 L ( w ) L(w) L(w)，如果需要的话，将损失函数调整为凸函数，以便求解最小值。
  5. 定义所使用的优化算法。
  6. 开始在epoches和batch上循环，执行优化算法：
    1. 调整数据结构，确定数据能够在神经网络、损失函数和优化算法中顺利执行。
    2. 完成前向传播，计算初始损失。
    3. 利用反向传播，在损失函数 L ( w ) L(w) L(w)上对每个 w w w求偏导
    4. 迭代当前权重，清空本轮梯度
    5. 完成模型进度与效果监控
  7. 输出结果

6.1 完整代码(CPU版)

python 复制代码 
import torch
from torch import nn
from torch import optim
from torch.nn import functional as F
from torch.utils.data import DataLoader, TensorDataset
import torchvision
import torchvision.transforms as transforms


# 确定数据、超参数
lr = 0.15
gamma = 0
epochs = 10
batch_size = 128

mnist = torchvision.datasets.FashionMNIST(
    root="./data",
    download=True,
    train=True,
    transform=transforms.ToTensor()
)  # 实例化数据

batch_data = DataLoader(
    mnist,
    batch_size=batch_size,
    shuffle=True
)

for x, y in batch_data:
    print(x.shape)
    print(y.shape)
    break

# x 四维 转化为二位 输入神经网络（128，28*28）
input = mnist.data[0].numel()
output = len(mnist.targets.unique())

class Model(nn.Module):
    def __init__(self, in_features=10, out_features=2):
        super().__init__()
        self.linear1 = nn.Linear(in_features, 128, bias=False)
        self.output = nn.Linear(128, out_features, bias=False)

    def forward(self, x):
        x = x.view(-1, 28*28) # 自动计算-1位置的维度 
        sigma1 = torch.relu(self.linear1(x))
        sigma2 = F.log_softmax(self.output(sigma1), dim=1)
        return sigma2

# 定义训练函数 包含损失函数、优化算法、梯度下降流程
def fit(net, batch_data, lr=0.01, epochs=5, gamma=0):
    criterion = nn.NLLLoss()  # 损失函数
    opt = optim.SGD(net.parameters(), lr=lr, momentum=gamma)
    correct = 0  # 预测正确的值为0
    samples = 0  # 循环开始之前，已查阅数量为0
    for epoch in range(epochs):
        for batch_id, (x, y) in enumerate(batch_data):
            y = y.view(x.shape[0])  # 降维
            sigma = net.forward(x)  # 正向传播
            loss = criterion(sigma, y)
            loss.backward()
            opt.step()
            opt.zero_grad()

            # 准确率
            y_hat = torch.max(sigma,1)[1]  # 按行获取预测结果中的最大值下标
            correct += torch.sum(y_hat == y)
            samples += x.shape[0]
            accuracy = float(correct / samples * 100)
        
            if (batch_id + 1) % 125 == 0 or (batch_id + 1) == len(batch_data):
               print(f"Epoch {epoch+1}: "
                     f"[{samples}/{epochs * len(batch_data.dataset)}] "  # 分子查看的数据量 分母总的需要查看数据量
                     f"({samples / (epochs * len(batch_data.dataset)) * 100:.0f}%) "
                     f"Loss: {loss.data.item():.6f} "
                     f"Accuracy: {accuracy:.3f}")

# 训练和评估
torch.manual_seed(520)
net = Model(in_features=input, out_features=output)
fit(net, batch_data, lr=lr, epochs=epochs, gamma=gamma)
bash 复制代码 
torch.Size([128, 1, 28, 28])
torch.Size([128])
Epoch 1: [16000/600000] (3%) Loss: 0.734373 Accuracy: 65.106
Epoch 1: [32000/600000] (5%) Loss: 0.676779 Accuracy: 70.956
Epoch 1: [48000/600000] (8%) Loss: 0.399305 Accuracy: 73.785
Epoch 1: [60000/600000] (10%) Loss: 0.528348 Accuracy: 75.202
Epoch 2: [76000/600000] (13%) Loss: 0.305862 Accuracy: 76.717
Epoch 2: [92000/600000] (15%) Loss: 0.367301 Accuracy: 77.766
Epoch 2: [108000/600000] (18%) Loss: 0.540866 Accuracy: 78.557
Epoch 2: [120000/600000] (20%) Loss: 0.427737 Accuracy: 79.127
Epoch 3: [136000/600000] (23%) Loss: 0.404156 Accuracy: 79.744
Epoch 3: [152000/600000] (25%) Loss: 0.471205 Accuracy: 80.305
Epoch 3: [168000/600000] (28%) Loss: 0.372120 Accuracy: 80.790
Epoch 3: [180000/600000] (30%) Loss: 0.327818 Accuracy: 81.076
Epoch 4: [196000/600000] (33%) Loss: 0.390757 Accuracy: 81.443
Epoch 4: [212000/600000] (35%) Loss: 0.499173 Accuracy: 81.807
Epoch 4: [228000/600000] (38%) Loss: 0.331916 Accuracy: 82.121
Epoch 4: [240000/600000] (40%) Loss: 0.213916 Accuracy: 82.320
Epoch 5: [256000/600000] (43%) Loss: 0.376595 Accuracy: 82.591
Epoch 5: [272000/600000] (45%) Loss: 0.294944 Accuracy: 82.854
Epoch 5: [288000/600000] (48%) Loss: 0.290940 Accuracy: 83.054
Epoch 5: [300000/600000] (50%) Loss: 0.463645 Accuracy: 83.199
Epoch 6: [316000/600000] (53%) Loss: 0.423245 Accuracy: 83.384
Epoch 6: [332000/600000] (55%) Loss: 0.391900 Accuracy: 83.587
Epoch 6: [348000/600000] (58%) Loss: 0.334901 Accuracy: 83.760
Epoch 6: [360000/600000] (60%) Loss: 0.401475 Accuracy: 83.887
Epoch 7: [376000/600000] (63%) Loss: 0.341380 Accuracy: 84.060
Epoch 7: [392000/600000] (65%) Loss: 0.348994 Accuracy: 84.216
Epoch 7: [408000/600000] (68%) Loss: 0.237210 Accuracy: 84.344
Epoch 7: [420000/600000] (70%) Loss: 0.473646 Accuracy: 84.434
Epoch 8: [436000/600000] (73%) Loss: 0.269989 Accuracy: 84.564
Epoch 8: [452000/600000] (75%) Loss: 0.374908 Accuracy: 84.703
Epoch 8: [468000/600000] (78%) Loss: 0.335344 Accuracy: 84.821
Epoch 8: [480000/600000] (80%) Loss: 0.416320 Accuracy: 84.896
Epoch 9: [496000/600000] (83%) Loss: 0.400059 Accuracy: 85.011
Epoch 9: [512000/600000] (85%) Loss: 0.352854 Accuracy: 85.119
Epoch 9: [528000/600000] (88%) Loss: 0.259676 Accuracy: 85.220
Epoch 9: [540000/600000] (90%) Loss: 0.207187 Accuracy: 85.286
Epoch 10: [556000/600000] (93%) Loss: 0.141855 Accuracy: 85.386
Epoch 10: [572000/600000] (95%) Loss: 0.366111 Accuracy: 85.464
Epoch 10: [588000/600000] (98%) Loss: 0.229552 Accuracy: 85.557
Epoch 10: [600000/600000] (100%) Loss: 0.334996 Accuracy: 85.623

6.2 完整代码(GPU版)

python 复制代码 
import torch
from torch import nn
from torch import optim
from torch.nn import functional as F
from torch.utils.data import DataLoader, TensorDataset
import torchvision
import torchvision.transforms as transforms


# 确定数据、超参数
lr = 0.15
gamma = 0
epochs = 10
batch_size = 128

# 检查CUDA是否可用并设置设备
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(f"Using device: {device}")

mnist = torchvision.datasets.FashionMNIST(
    root="./data",
    download=True,
    train=True,
    transform=transforms.ToTensor()
)  # 实例化数据

batch_data = DataLoader(
    mnist,
    batch_size=batch_size,
    shuffle=True
)

for x, y in batch_data:
    print(x.shape)
    print(y.shape)
    break

# x 四维 转化为二位 输入神经网络（128，28*28）
input = mnist.data[0].numel()
output = len(mnist.targets.unique())

class Model(nn.Module):
    def __init__(self, in_features=10, out_features=2):
        super().__init__()
        self.linear1 = nn.Linear(in_features, 128, bias=False)
        self.output = nn.Linear(128, out_features, bias=False)

    def forward(self, x):
        x = x.view(-1, 28*28) # 自动计算-1位置的维度 
        sigma1 = torch.relu(self.linear1(x))
        sigma2 = F.log_softmax(self.output(sigma1), dim=1)
        return sigma2

# 定义训练函数 包含损失函数、优化算法、梯度下降流程
def fit(net, batch_data, lr=0.01, epochs=5, gamma=0):
    criterion = nn.NLLLoss()  # 损失函数
    opt = optim.SGD(net.parameters(), lr=lr, momentum=gamma)
    correct = 0  # 预测正确的值为0
    samples = 0  # 循环开始之前，已查阅数量为0
    for epoch in range(epochs):
        for batch_id, (x, y) in enumerate(batch_data):
            # 将数据和标签移动到设备
            x, y = x.to(device), y.to(device)
            y = y.view(x.shape[0])  # 降维
            sigma = net.forward(x)  # 正向传播
            loss = criterion(sigma, y)
            loss.backward()
            opt.step()
            opt.zero_grad()

            # 准确率
            y_hat = torch.max(sigma,1)[1]  # 按行获取预测结果中的最大值下标
            correct += torch.sum(y_hat == y)
            samples += x.shape[0]
            accuracy = float(correct / samples * 100)
        
            if (batch_id + 1) % 125 == 0 or (batch_id + 1) == len(batch_data):
               print(f"Epoch {epoch+1}: "
                     f"[{samples}/{epochs * len(batch_data.dataset)}] "  # 分子查看的数据量 分母总的需要查看数据量
                     f"({samples / (epochs * len(batch_data.dataset)) * 100:.0f}%) "
                     f"Loss: {loss.data.item():.6f} "
                     f"Accuracy: {accuracy:.3f}")

# 训练和评估
torch.manual_seed(520)
net = Model(in_features=input, out_features=output)
# 将模型移动到设备
net = net.to(device)
fit(net, batch_data, lr=lr, epochs=epochs, gamma=gamma)
bash 复制代码 
Using device: cuda
torch.Size([128, 1, 28, 28])
torch.Size([128])
Epoch 1: [16000/600000] (3%) Loss: 0.734373 Accuracy: 65.106
Epoch 1: [32000/600000] (5%) Loss: 0.676779 Accuracy: 70.956
Epoch 1: [48000/600000] (8%) Loss: 0.399305 Accuracy: 73.785
Epoch 1: [60000/600000] (10%) Loss: 0.528348 Accuracy: 75.202
Epoch 2: [76000/600000] (13%) Loss: 0.305862 Accuracy: 76.717
Epoch 2: [92000/600000] (15%) Loss: 0.367301 Accuracy: 77.766
Epoch 2: [108000/600000] (18%) Loss: 0.540866 Accuracy: 78.557
Epoch 2: [120000/600000] (20%) Loss: 0.431061 Accuracy: 79.121
Epoch 3: [136000/600000] (23%) Loss: 0.401790 Accuracy: 79.749
Epoch 3: [152000/600000] (25%) Loss: 0.464959 Accuracy: 80.312
Epoch 3: [168000/600000] (28%) Loss: 0.365807 Accuracy: 80.801
Epoch 3: [180000/600000] (30%) Loss: 0.327237 Accuracy: 81.089
Epoch 4: [196000/600000] (33%) Loss: 0.390030 Accuracy: 81.452
Epoch 4: [212000/600000] (35%) Loss: 0.496652 Accuracy: 81.817
Epoch 4: [228000/600000] (38%) Loss: 0.331042 Accuracy: 82.121
Epoch 4: [240000/600000] (40%) Loss: 0.213194 Accuracy: 82.320
Epoch 5: [256000/600000] (43%) Loss: 0.370124 Accuracy: 82.586
Epoch 5: [272000/600000] (45%) Loss: 0.292856 Accuracy: 82.850
Epoch 5: [288000/600000] (48%) Loss: 0.292363 Accuracy: 83.050
Epoch 5: [300000/600000] (50%) Loss: 0.460225 Accuracy: 83.196
Epoch 6: [316000/600000] (53%) Loss: 0.425557 Accuracy: 83.390
Epoch 6: [332000/600000] (55%) Loss: 0.391748 Accuracy: 83.587
Epoch 6: [348000/600000] (58%) Loss: 0.338550 Accuracy: 83.762
Epoch 6: [360000/600000] (60%) Loss: 0.415630 Accuracy: 83.888
Epoch 7: [376000/600000] (63%) Loss: 0.339880 Accuracy: 84.065
Epoch 7: [392000/600000] (65%) Loss: 0.349333 Accuracy: 84.220
Epoch 7: [408000/600000] (68%) Loss: 0.239564 Accuracy: 84.344
Epoch 7: [420000/600000] (70%) Loss: 0.478126 Accuracy: 84.432
Epoch 8: [436000/600000] (73%) Loss: 0.269563 Accuracy: 84.563
Epoch 8: [452000/600000] (75%) Loss: 0.371759 Accuracy: 84.699
Epoch 8: [468000/600000] (78%) Loss: 0.336216 Accuracy: 84.816
Epoch 8: [480000/600000] (80%) Loss: 0.418535 Accuracy: 84.888
Epoch 9: [496000/600000] (83%) Loss: 0.397247 Accuracy: 85.003
Epoch 9: [512000/600000] (85%) Loss: 0.358816 Accuracy: 85.111
Epoch 9: [528000/600000] (88%) Loss: 0.262421 Accuracy: 85.213
Epoch 9: [540000/600000] (90%) Loss: 0.206387 Accuracy: 85.279
Epoch 10: [556000/600000] (93%) Loss: 0.145811 Accuracy: 85.379
Epoch 10: [572000/600000] (95%) Loss: 0.361493 Accuracy: 85.461
Epoch 10: [588000/600000] (98%) Loss: 0.234481 Accuracy: 85.560
相关推荐
信息快讯11 小时前
【机器学习赋能的智能光子学器件系统研究与应用】
人工智能·神经网络·机器学习·光学
IT小哥哥呀13 小时前
基于深度学习的数字图像分类实验与分析
人工智能·深度学习·分类
汉堡go14 小时前
1、机器学习与深度学习
人工智能·深度学习·机器学习
LiJieNiub15 小时前
基于 PyTorch 实现 MNIST 手写数字识别
pytorch·深度学习·学习
chxin1401616 小时前
Transformer注意力机制——动手学深度学习10
pytorch·rnn·深度学习·transformer
lljss202016 小时前
5. 神经网络的学习
人工智能·神经网络·学习
jie*16 小时前
小杰深度学习（fourteen）——视觉-经典神经网络——ResNet
人工智能·python·深度学习·神经网络·机器学习·tensorflow·lstm
jie*16 小时前
小杰深度学习（sixteen）——视觉-经典神经网络——MobileNetV2
人工智能·python·深度学习·神经网络·tensorflow·numpy·matplotlib
MYX_30916 小时前
第五章 神经网络的优化
pytorch·深度学习·神经网络·学习
TGITCIC16 小时前
有趣的机器学习-利用神经网络来模拟“古龙”写作风格的输出器
人工智能·深度学习·神经网络·ai大模型·模型训练·训练模型·手搓模型
热门推荐
01两千字总结：Codex 国内如何安装和使用的教程，以及如何设置中文回答02BongoCat - 跨平台键盘猫动画工具03GitHub 镜像站点04UV安装并设置国内源05GitLab 零基础入门指南：从安装到项目管理全流程06Linux下V2Ray安装配置指南0746个Nano-banana 精选提示词，持续更新中08智能库存管理的需求预测模型：从业务痛点到落地代码的完整实践092025羊城杯网络安全大赛 wp10UV 工具安装与国内镜像源配置指南