Python进阶指南7:排序算法和树

PKNLP2025-09-24 16:10

1.排序算法

1.1算法稳定性

所谓排序，使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作

排序算法，就是如何使得记录按照要求排列的方法

排序算法在很多领域是非常重要

在大量数据的处理方面：一个优秀的算法可以节省大量的资源。

在各个领域中考虑到数据的各种限制和规范，要得到一个符合实际的优秀算法，得经过大量的推理和分析

举个例子：

把以上数据进行升序排列：

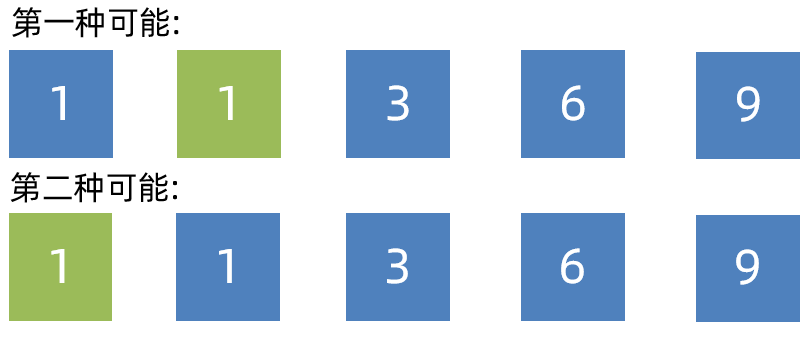
☆ 假定在待排序的记录序列中，存在多个具有相同的关键字的记录

☆ 若经过排序，这些记录的相对次序保持不变,则称这种排序算法是稳定的, 否则称为不稳定的

记忆：具有相同关键字的纪录经过排序后，相对位置保持不变，这样的算法是稳定性算法

再来看一个例子：

升序排序后的结果

无序数据具有2个关键字，

先按照关键字1排序，

若关键字1值相同，再按照关键字2排序。

稳定性算法具有良好的作用。

1.2排序算法

排序犹如一把将混乱变为秩序的魔法钥匙，使我们能以更高效的方式理解与处理数据。

无论是简单的升序，还是复杂的分类排列，排序都向我们展示了数据的和谐美感。

☆ 冒泡排序
冒泡思路

冒泡排序（bubble sort）通过连续地比较与交换相邻元素实现排序。这个过程就像气泡从底部升到顶部一样，因此得名冒泡排序。

可视化展示网站：https://visualgo.net/zh/sorting

冒泡过程可以利用元素交换操作来模拟：从数组最左端开始向右遍历，依次比较相邻元素大小，如果"左元素 > 右元素"就交换二者。遍历完成后，最大的元素会被移动到数组的最右端。

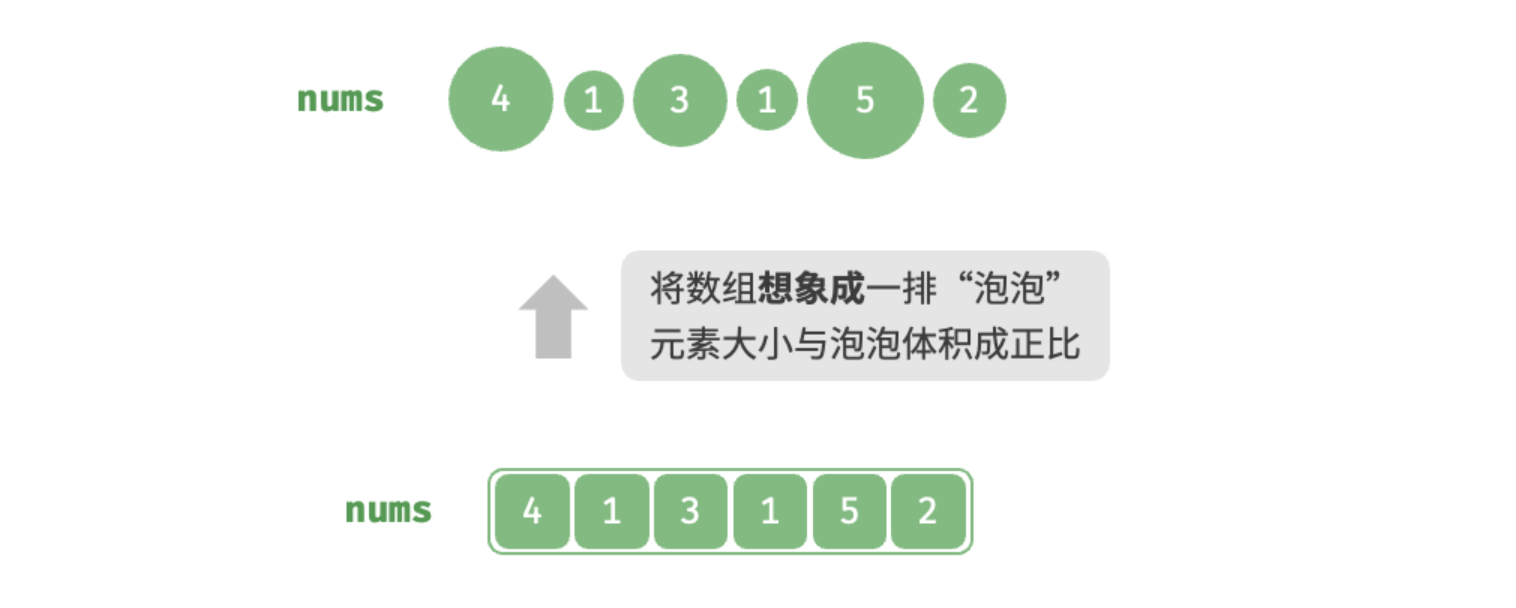
第一轮第一步排序：

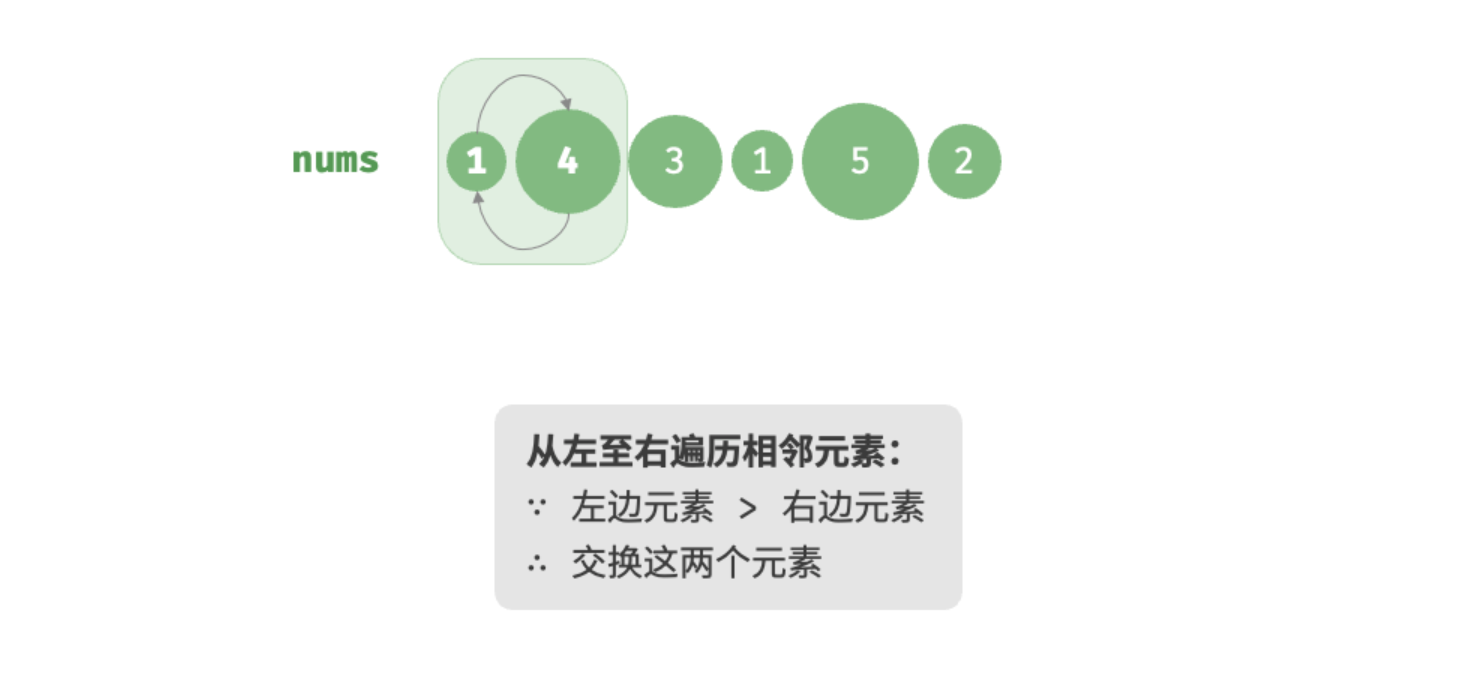
第一轮第二步排序：

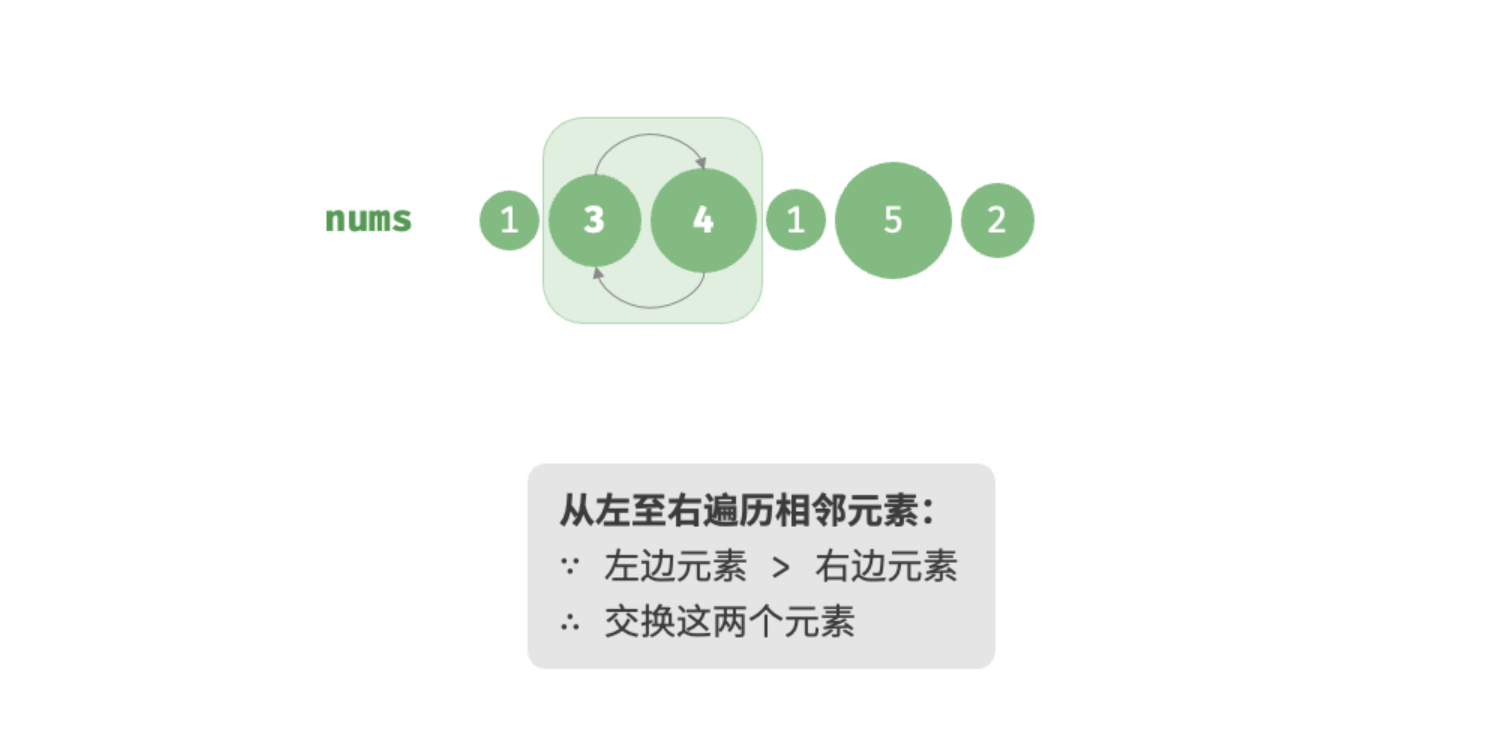
第一轮第三步排序：

第一轮第四步排序：

第一轮第五步排序：

第一轮最终排序结果：

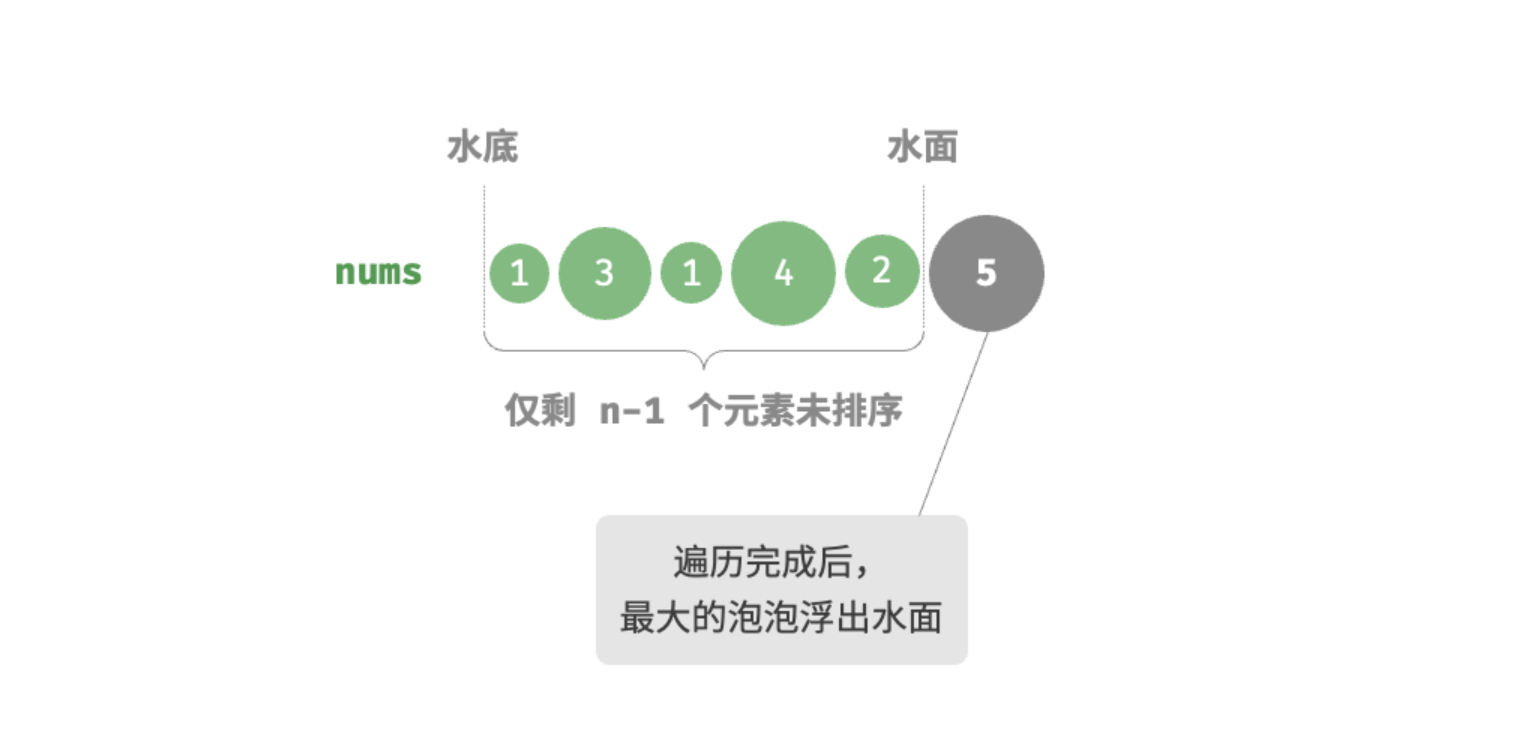
重复以上步骤，直至完成最终排序。

冒泡步骤

设列表的长度为 n ，冒泡排序的步骤如上图所示。

  1. 首先，对 n 个元素执行"冒泡"，将列表的最大元素交换至正确位置。
  2. 接下来，对剩余 n−1 个元素执行"冒泡"，将第二大元素交换至正确位置。
  3. 以此类推，经过 n−1 轮"冒泡"后，前 n−1 大的元素都被交换至正确位置。
  4. 仅剩的一个元素必定是最小元素，无须排序，因此列表排序完成。
代码实现
python 复制代码 
# 冒泡排序
def bubble_sort(my_list):
    # 获取列表的元素个数
    list_length = len(my_list)

    """
        以[5,3,4,7,2]
        注意：排完序以后，小的在前，大的在后。当前遍历到的元素与后一个元素进行对比和交互
        第一轮循环：i=0，list_length=5
            内层循环：j元素的索引初始值=0，j要循环到【索引为3】结束
            j=3，元素是7，后一个元素的索引=j+1
            
            结合上面的注意实现，得到内层循环要list_length-1
            
        第一轮循环的结果：[3,4,5,2,7]
        
        第二轮循环：i=1，list_length=5，列表中的最后的元素7不用再纳入下一次循环
            内层循环：j元素的索引初始值=0，j要循环到【索引为2】结束
            因此最终内层循环的range的表达式要写出list_length-1-1
            
        第二轮循环的结果：[3,4,2,5,7]
        
        第三轮循环：i=2，list_length=5，列表中的最后的元素5,7不用再纳入下一次循环
            内层循环：j元素的索引初始值=0，j要循环到【索引为1】结束
            因此最终内层循环的range的表达式要写出list_length-1-2
            
        综上所述：因此最终内层循环的range的表达式要写出list_length-1-i
    """
    for i in range(list_length):
        # 外层循环控制循环的次数

        for j in range(list_length-1-i):
            # 内层循环控制每轮中各个元素值的大小对比

            if my_list[j]>my_list[j+1]:
                # 交互两个元素的值
                my_list[j],my_list[j+1] = my_list[j+1],my_list[j]

if __name__ == '__main__':
    my_list = [5,3,4,7,2]
    bubble_sort(my_list)
    print(my_list)
效率优化

我们发现，如果某轮"冒泡"中没有执行任何交换操作，说明数组已经完成排序，可直接返回结果。因此，可以增加一个标志位 flag 来监测这种情况，一旦出现就立即返回。

经过优化，冒泡排序的最差时间复杂度和平均时间复杂度仍为 O(n2) ；但当输入数组完全有序时，可达到最佳时间复杂度 O(n)

python 复制代码 
# 冒泡排序
def bubble_sort(my_list):
    # 获取列表的元素个数
    list_length = len(my_list)

    """
        以[5,3,4,7,2]
        注意：排完序以后，小的在前，大的在后。当前遍历到的元素与后一个元素进行对比和交互
        第一轮循环：i=0，list_length=5
            内层循环：j元素的索引初始值=0，j要循环到【索引为3】结束
            j=3，元素是7，后一个元素的索引=j+1
            
            结合上面的注意实现，得到内层循环要list_length-1
            
        第一轮循环的结果：[3,4,5,2,7]
        
        第二轮循环：i=1，list_length=5，列表中的最后的元素7不用再纳入下一次循环
            内层循环：j元素的索引初始值=0，j要循环到【索引为2】结束
            因此最终内层循环的range的表达式要写出list_length-1-1
            
        第二轮循环的结果：[3,4,2,5,7]
        
        第三轮循环：i=2，list_length=5，列表中的最后的元素5,7不用再纳入下一次循环
            内层循环：j元素的索引初始值=0，j要循环到【索引为1】结束
            因此最终内层循环的range的表达式要写出list_length-1-2
            
        综上所述：因此最终内层循环的range的表达式要写出list_length-1-i
    """

    # 是否有元素交互。False表示没有，True表示有
    flag = False
    for i in range(list_length-1):
        print(f"外层循环{i}")
        # 外层循环控制循环的次数

        for j in range(list_length-1-i):
            # 内层循环控制每轮中各个元素值的大小对比

            if my_list[j]>my_list[j+1]:
                # 交互两个元素的值
                my_list[j],my_list[j+1] = my_list[j+1],my_list[j]
                flag = True

        # 为什么能够直接在这里判断然后结束循环。核心原因是冒泡排序的第一轮循环会得到最大值
        # 如果第一轮循环的过程中，都没有发生交换。那么后续更加不可能有交换
        if not flag:
            break


if __name__ == '__main__':
    # my_list = [5,3,4,7,2]
    my_list = [1,2,3,4]
    bubble_sort(my_list)
    print(my_list)
☆ 选择排序

选择排序（selection sort）的工作原理非常简单：开启一个循环，每轮从未排序区间选择最小的元素，将其放到已排序区间的末尾。

排序思路

设列表的长度为 n ，选择排序的算法流程如下图所示：

第一轮：

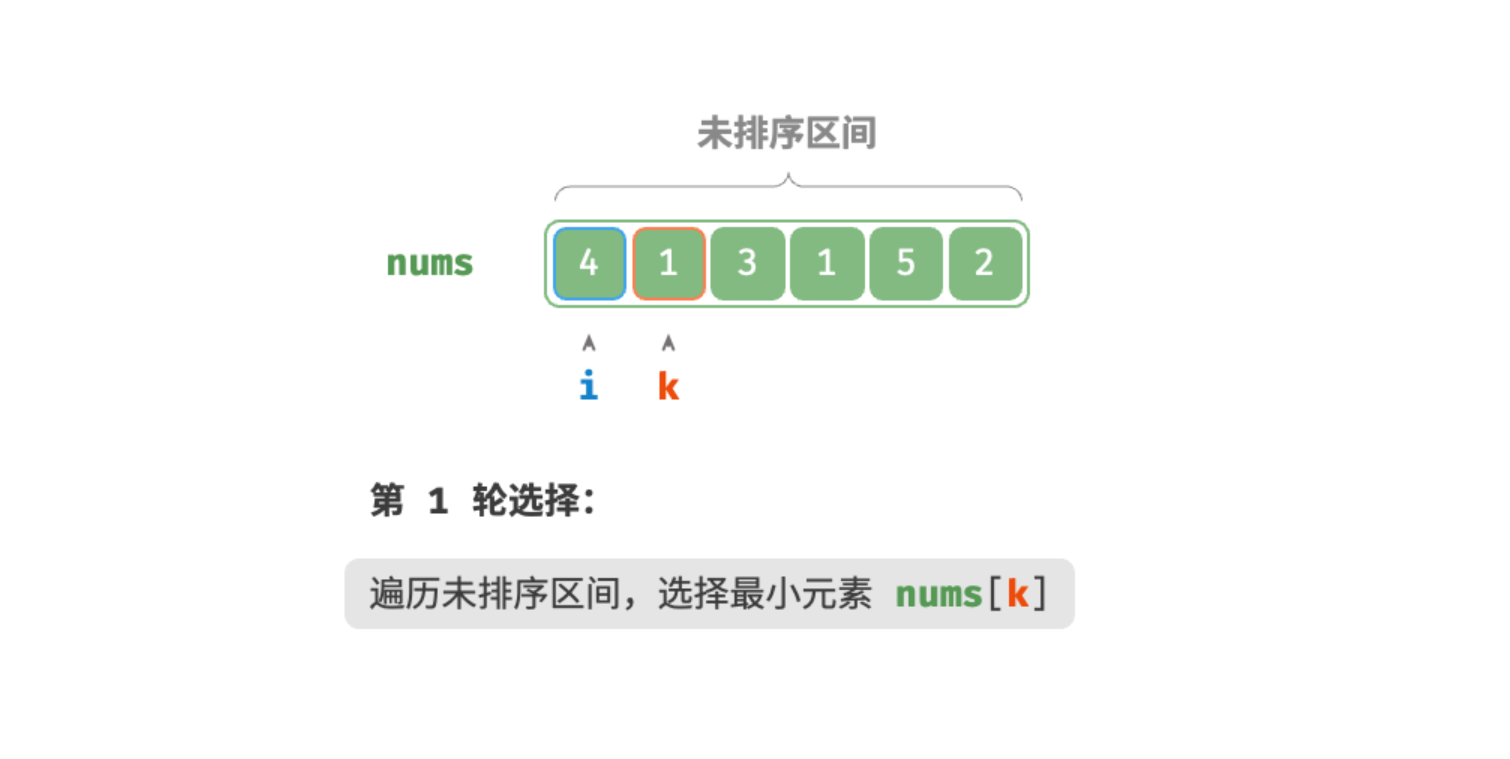
第一轮：

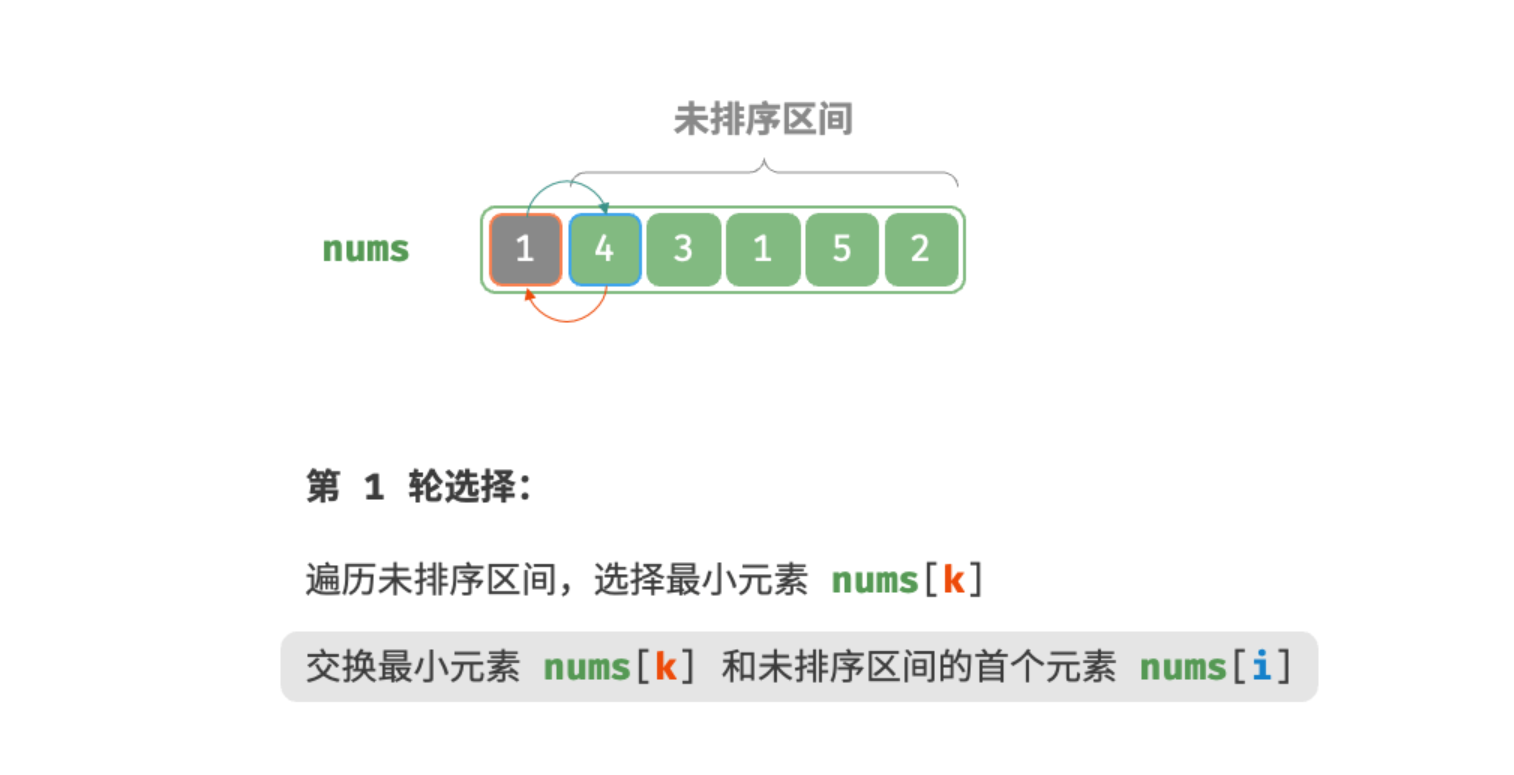
第二轮：

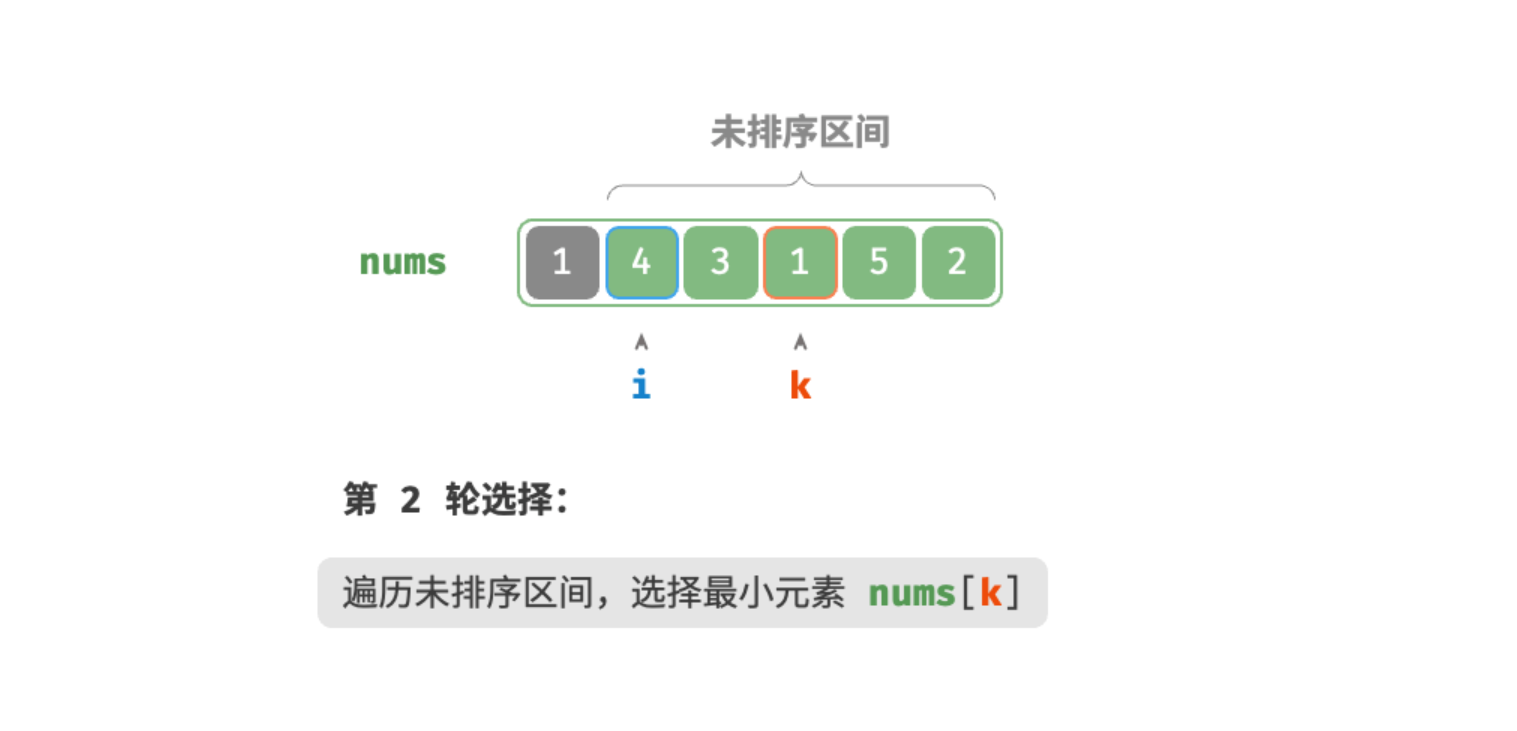
第二轮：

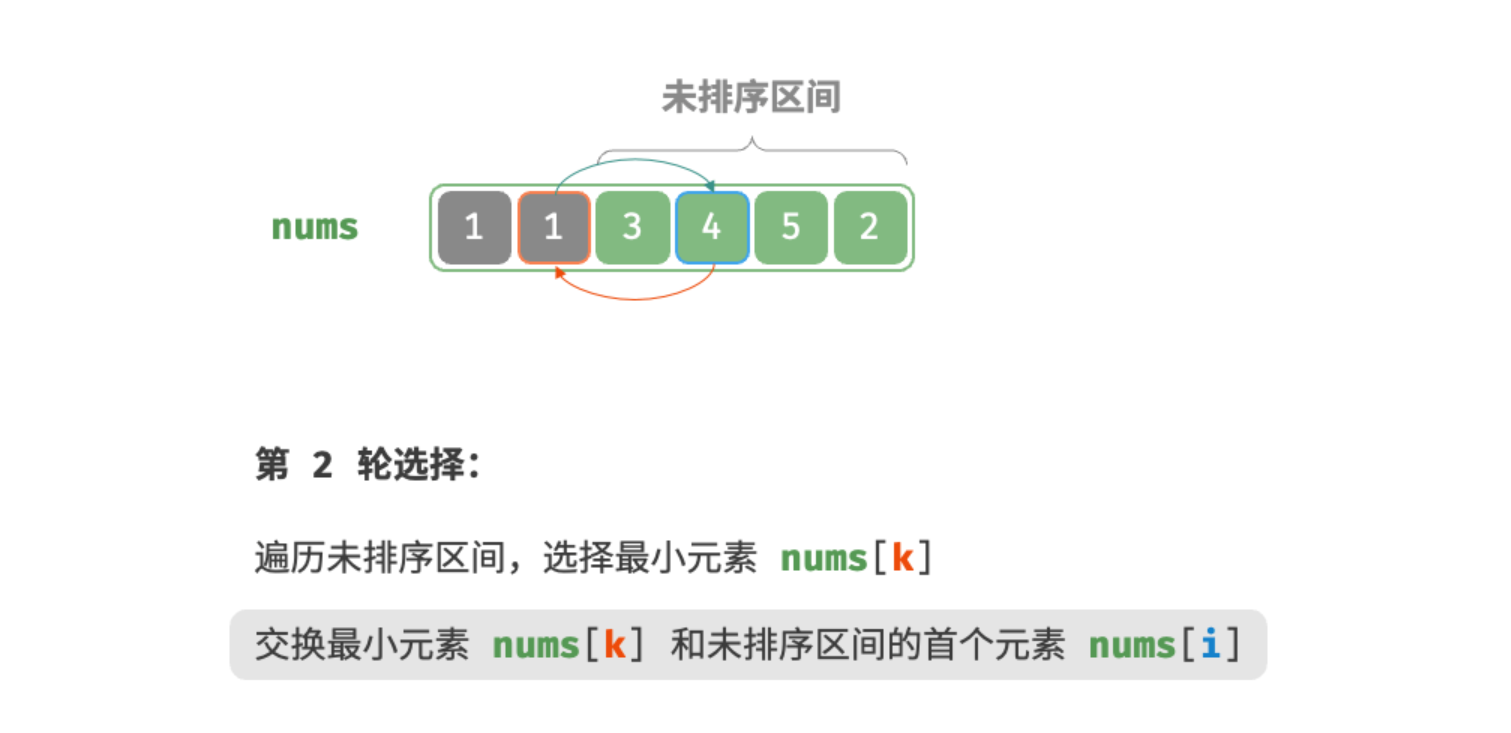
第三轮：

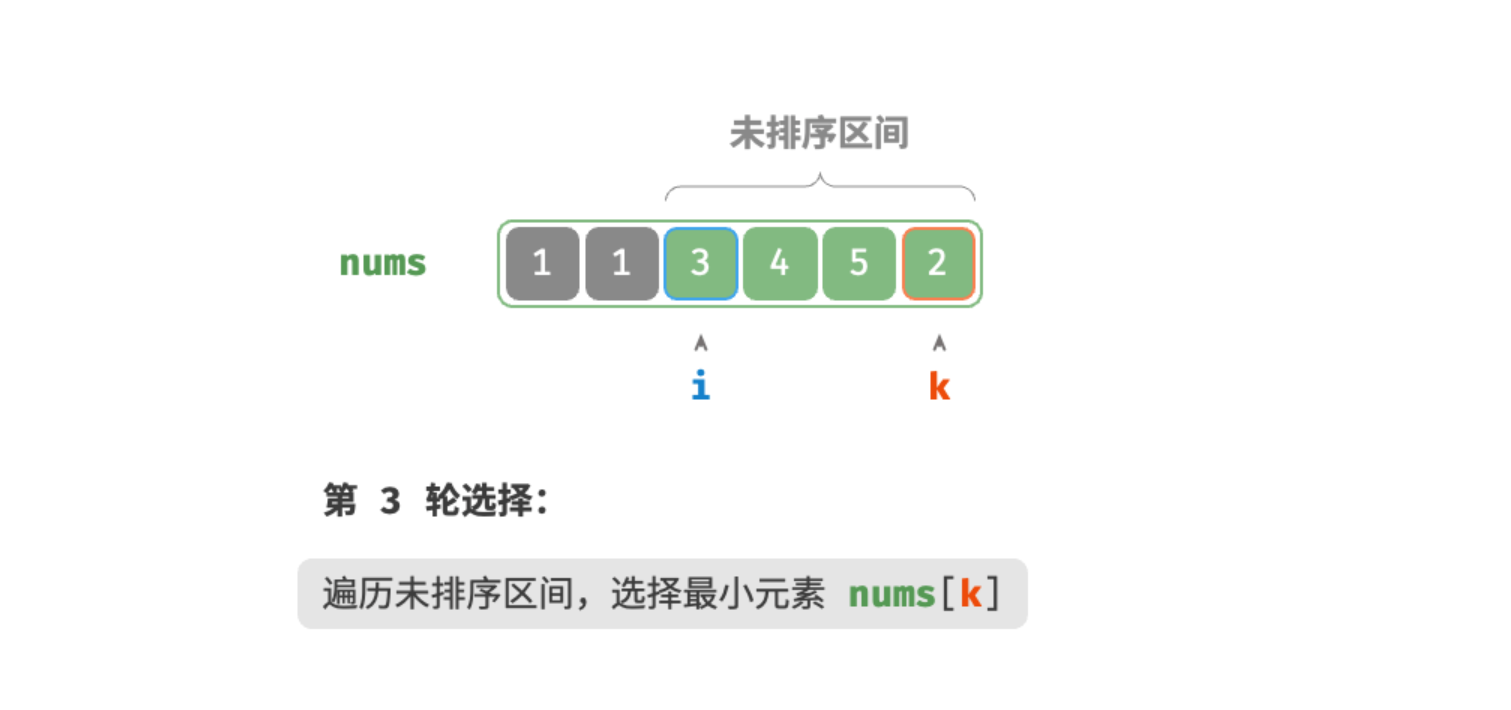
第三轮：

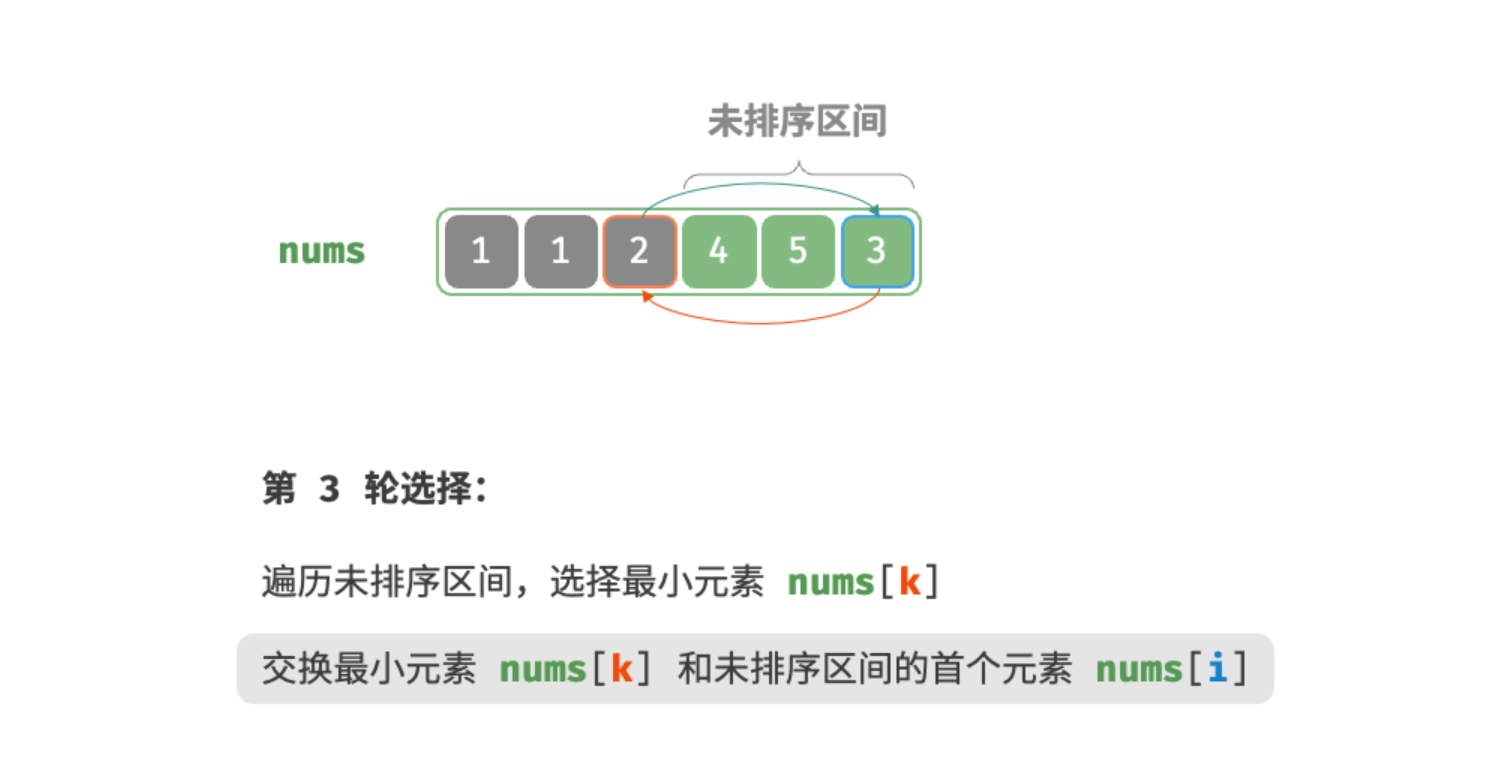
第四轮：

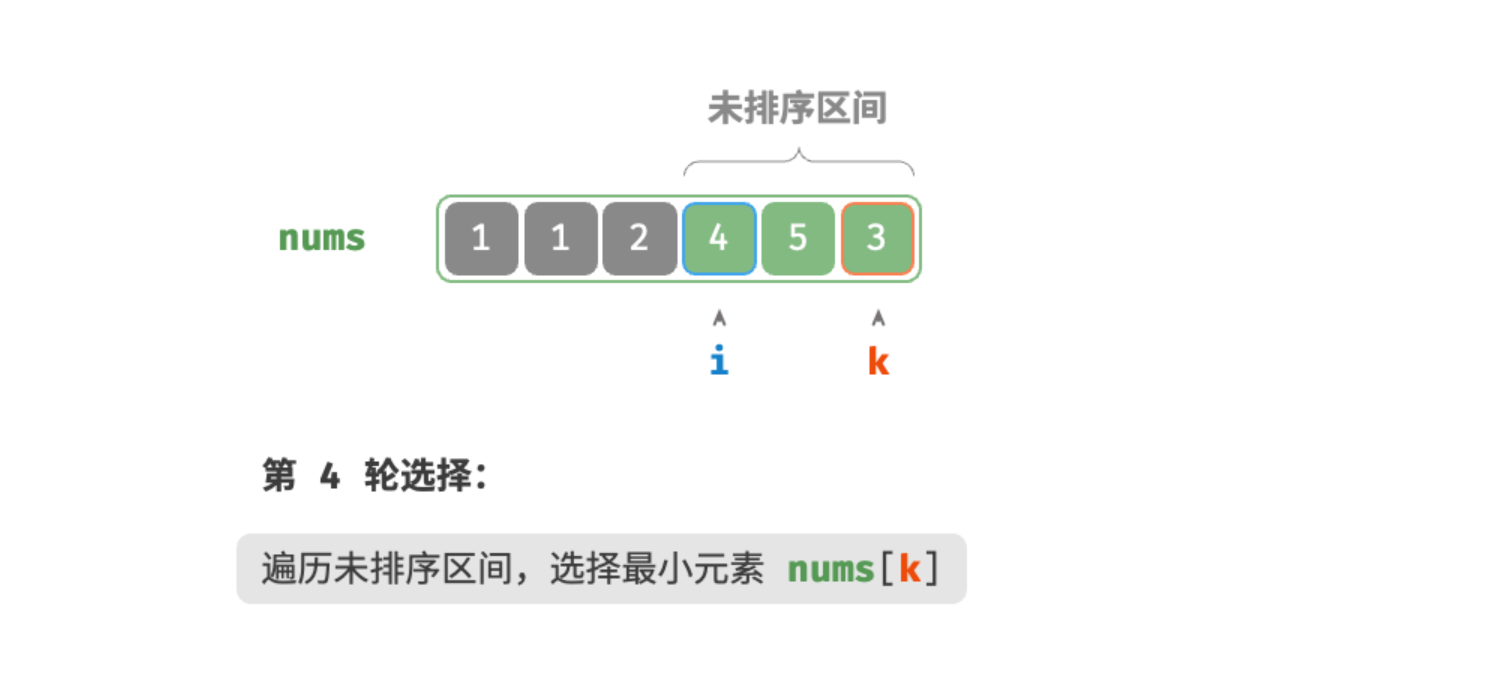
第四轮：

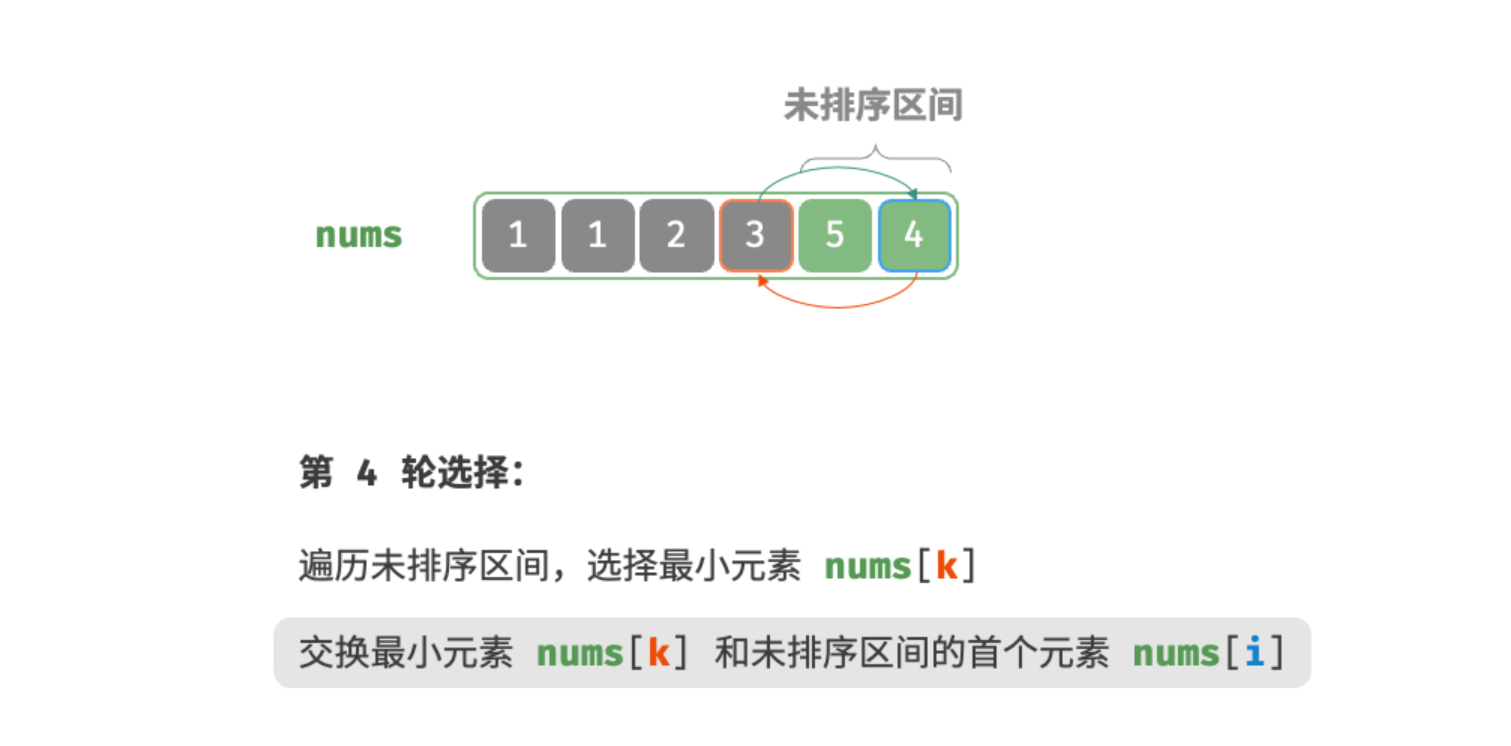
第五轮：

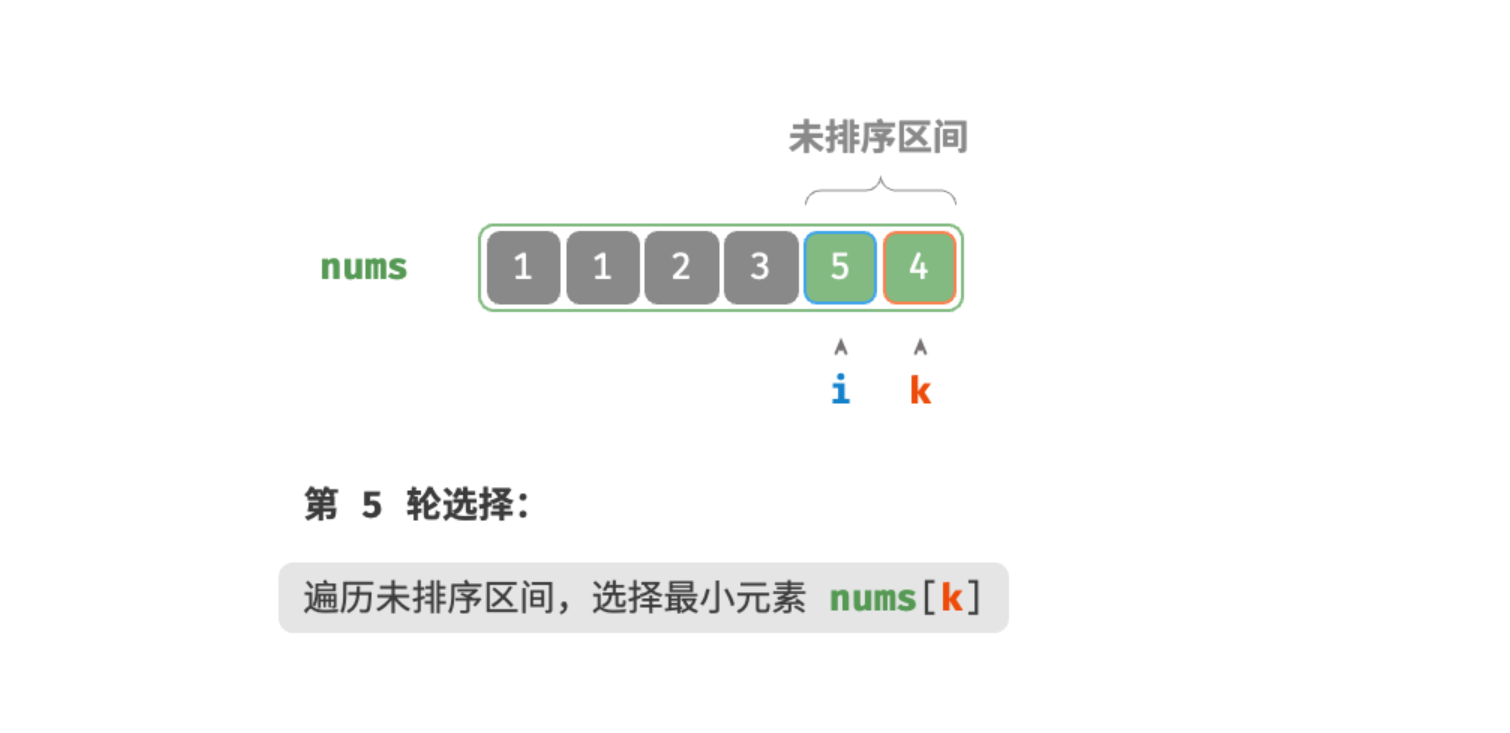
第五轮：

完成排序，最终结果：

排序步骤
  1. 初始状态下，所有元素未排序，即未排序（索引）区间为 [0,n−1] 。
  2. 选取区间 [0,n−1] 中的最小元素，将其与索引 0 处的元素交换。完成后，数组前 1 个元素已排序。
  3. 选取区间 [1,n−1] 中的最小元素，将其与索引 1 处的元素交换。完成后，数组前 2 个元素已排序。
  4. 以此类推。经过 n−1 轮选择与交换后，数组前 n−1 个元素已排序。
  5. 仅剩的一个元素必定是最大元素，无须排序，因此数组排序完成。
代码实现
python 复制代码 
def select_sort(my_list):

    # 获取列表的元素个数
    list_length = len(my_list)

    for i in range(list_length-1):
        # 外层循环控制排序轮次

        """
            以[5, 3, 4, 7, 2]为例。list_length固定值为5
            
            第一轮：i=0，临时的最小值初始化是5，那么需要拿3，4，7，2与该值进行大小比较
                因此，j的初始化索引=1，直到=list_length-1结束
                第一轮的结果：[2,3,4,7,5]    
            
            第二轮：i=1，临时的最小值初始化是3，那么需要拿4,7,5与该值进行大小比较
                因此，j的初始化索引=2，直到=list_length-1结束
                
            所以：内层循环的range中表达式range(i+1,list_length)
        """
        # 临时的最小值的索引
        min_index = i
        for j in range(i+1,list_length):
            # 内层循环用来在剩余的数据中找到最小值

            # 比较大小。如果当前的元素值比临时的最小值要小，更新最小值的索引
            if my_list[j]<my_list[min_index]:
                min_index = j

        # 经过上面的循环以后能够找到本轮的最小值索引，然后调整元素的索引
        if min_index!=i:
            my_list[min_index],my_list[i] = my_list[i],my_list[min_index]

if __name__ == '__main__':
    my_list = [5, 3, 4, 7, 2]
    # my_list = [1, 2, 3, 4]
    select_sort(my_list)
    print(my_list)

2.树

2.1树的基本概念

树是一种一对多关系的数据结构，主要分为：

  1. 多叉树
    1. 每个结点有0、或者多个子节点
    2. 没有父节点的结点成为根节点
    3. 每一个非根节点有且只有一个父节点
    4. 除了根节点外，每个子节点可以分为多个互不相交的子树
  2. 二叉树
    1. 每个结点有0、1、2 个子节点
    2. 没有父节点的结点成为根节点
    3. 每一个非根节点有且只有一个父节点
    4. 除了根节点外，每个子节点可以分为多个互不相交的子树

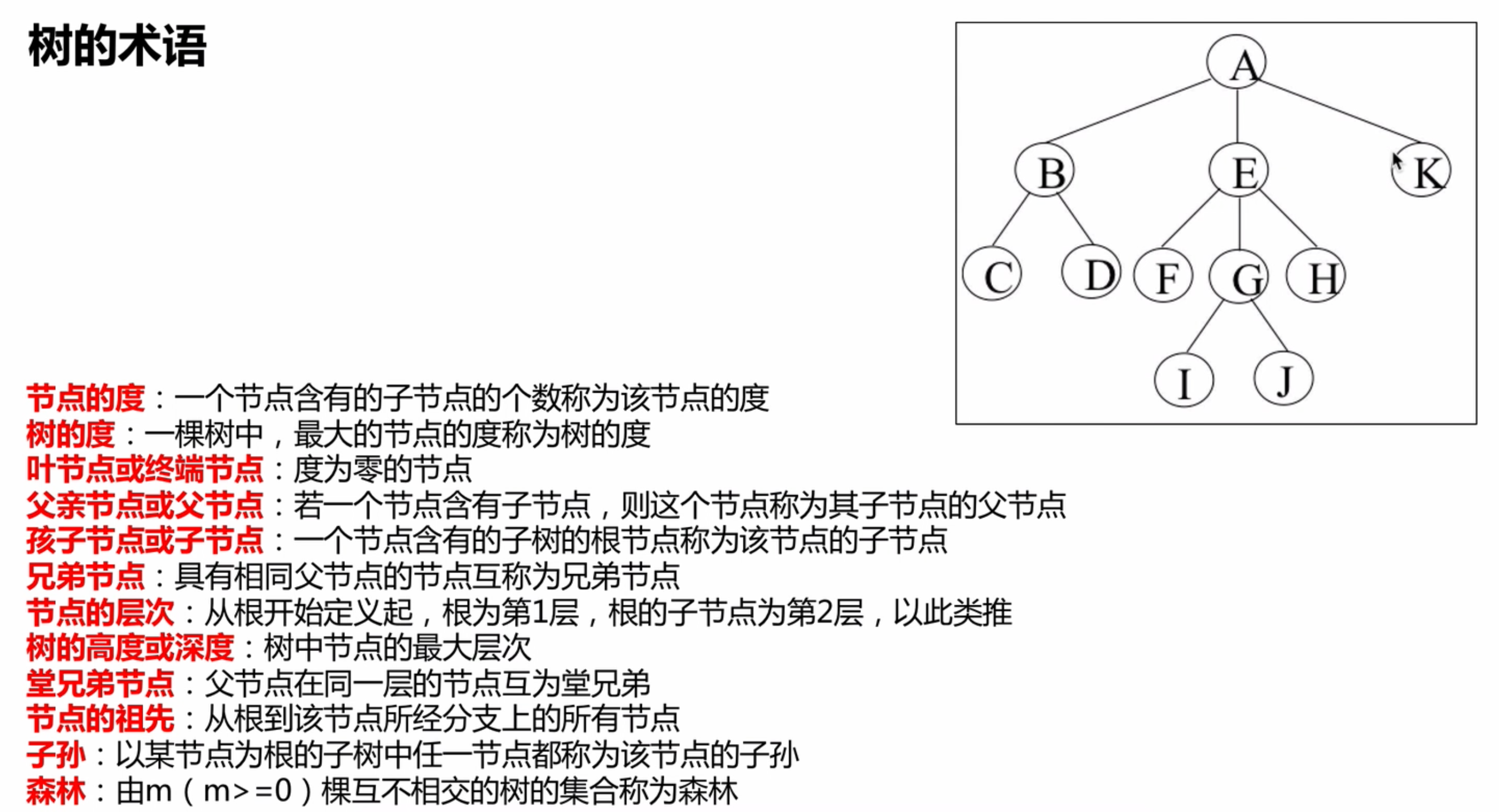
2.2树的相关术语

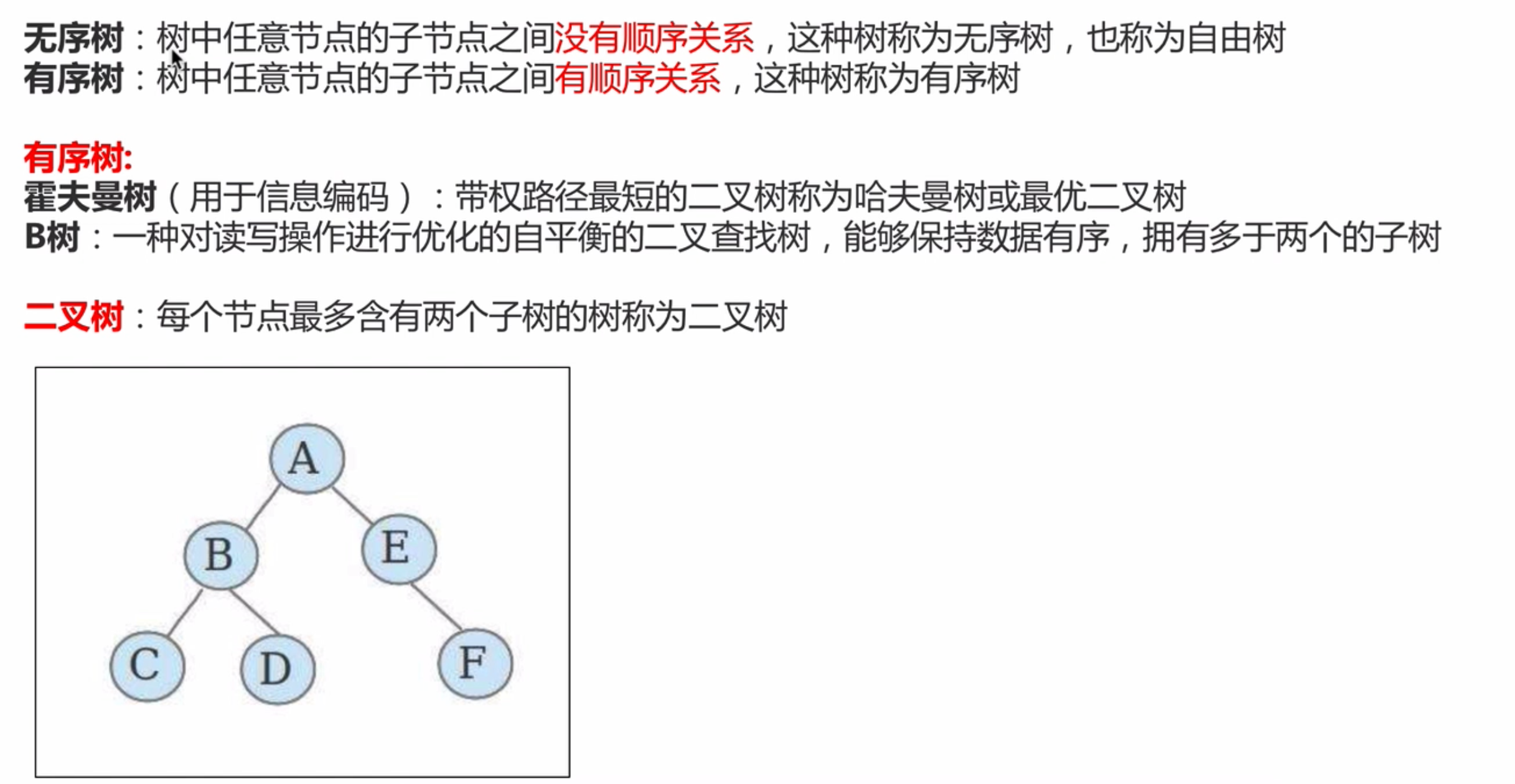
2.3二叉树的种类


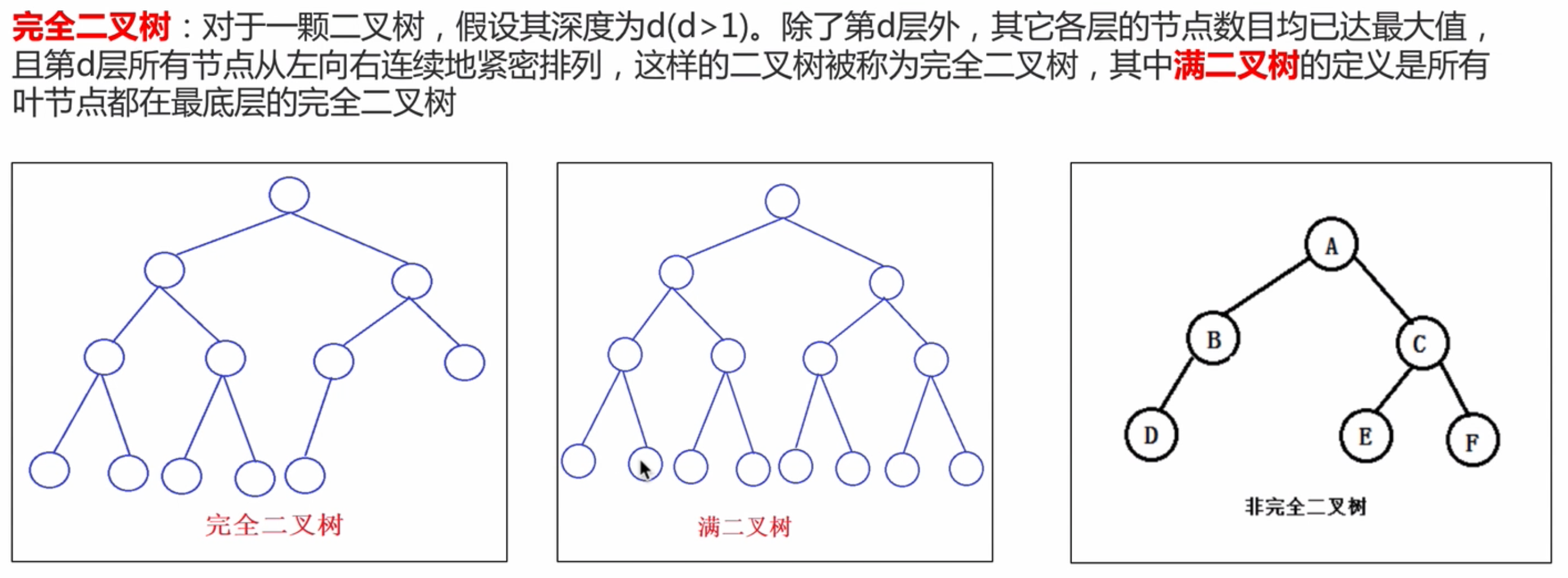
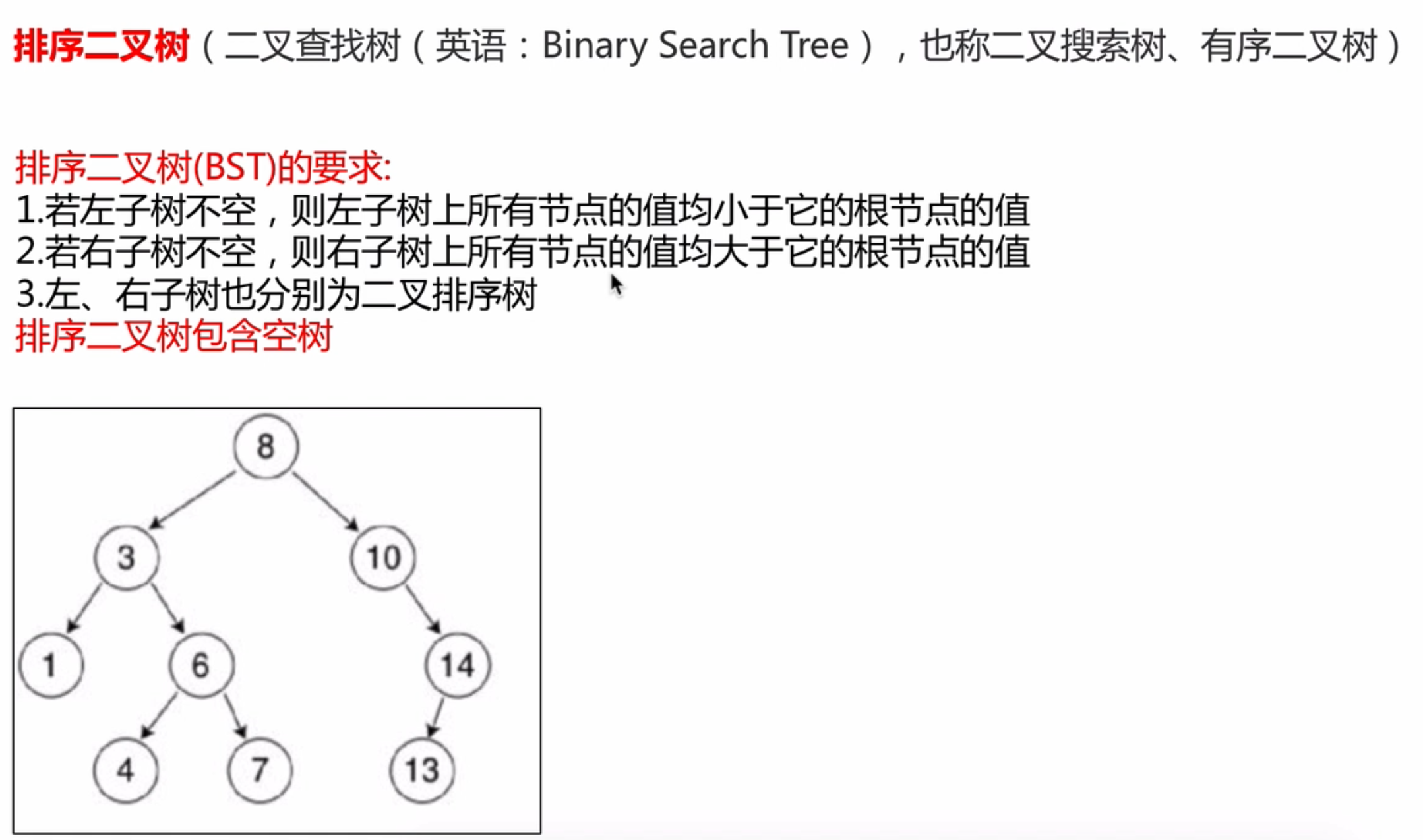
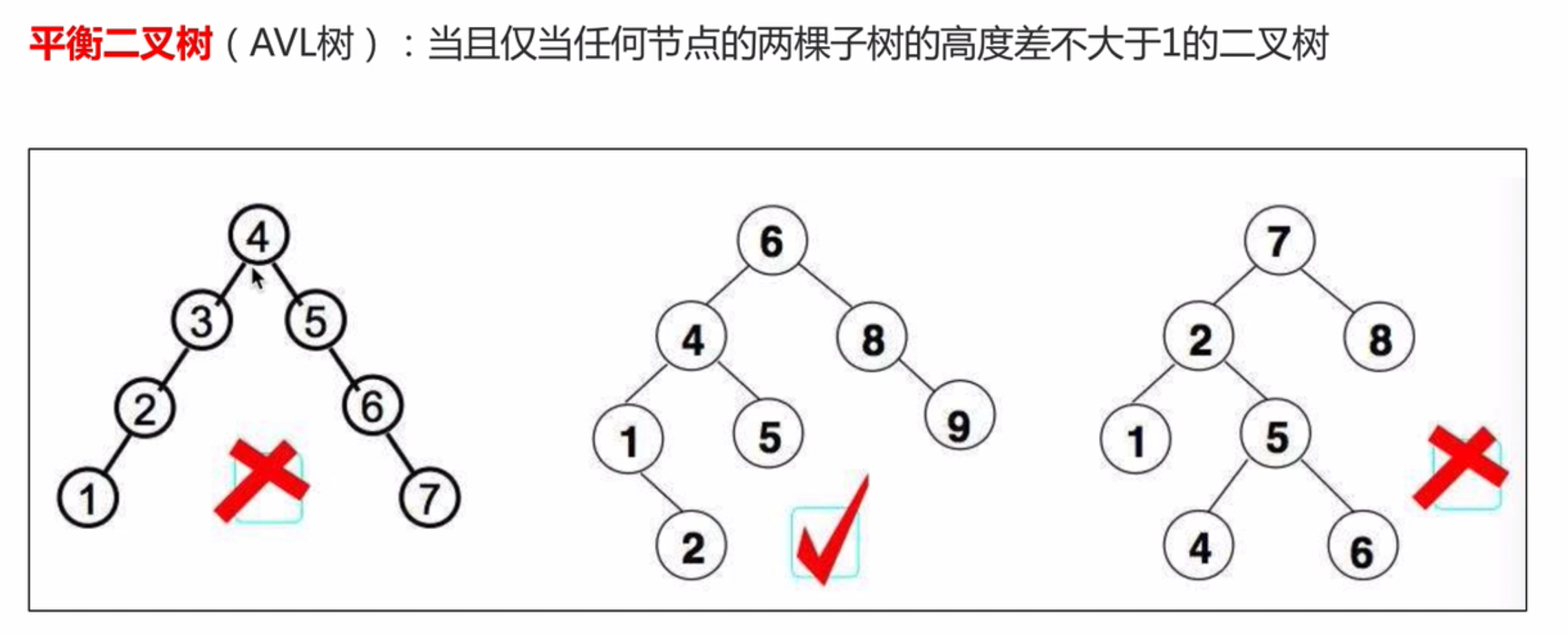
2.4二叉树的存储

顺序存储、链式存储。树在存储的时候，要存储什么？

  1. 值
  2. 结点关系

如果树是完全二叉树、满二叉树，可以使用顺序存储。大多数构建出的树都不是完全、满二叉树，所以使用链式存储比较多。

python 复制代码 
class TreeNode:
  
  def __init__(self):
    self.item = value
    self.parent = 父亲
    self.lchild = 左边树
    self.rchild = 右边树

对于树而言，只要拿到根节点，就相当于拿到整棵树。

完全二叉树适合顺序结构存储，但其插入删除元素效率较差。

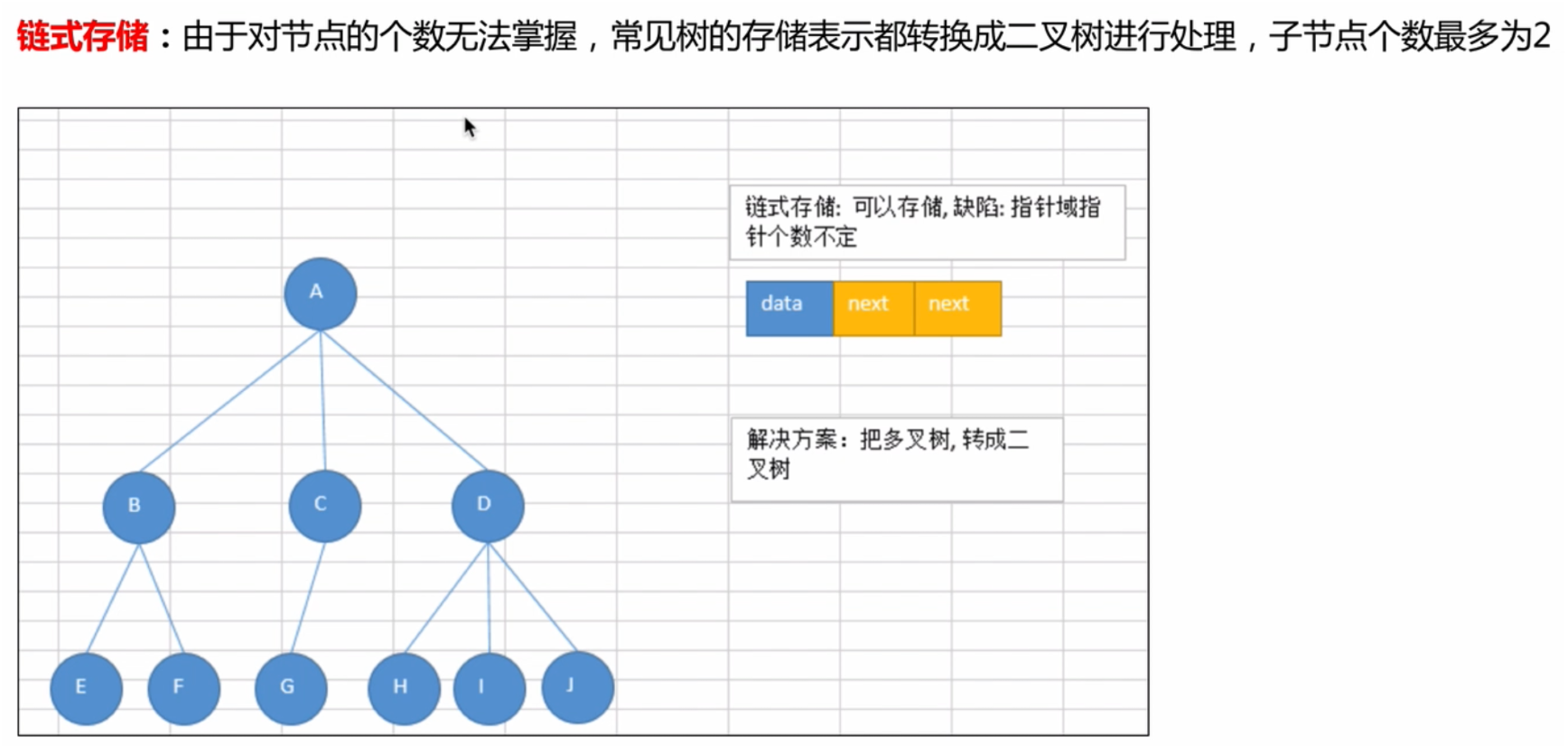
大多数的二叉树都是使用链式结构存储。

2.5树的应用场景_数据库索引

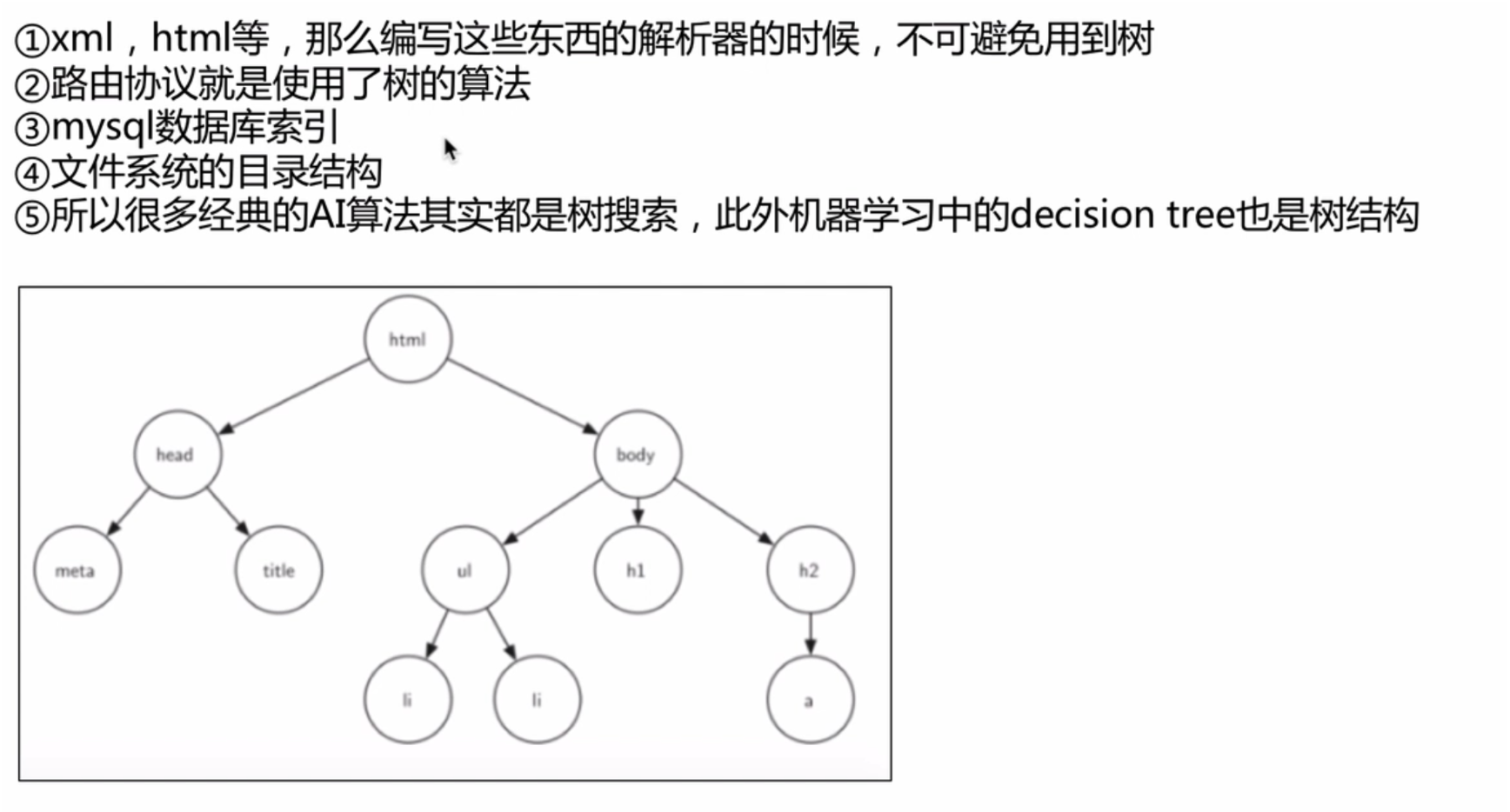
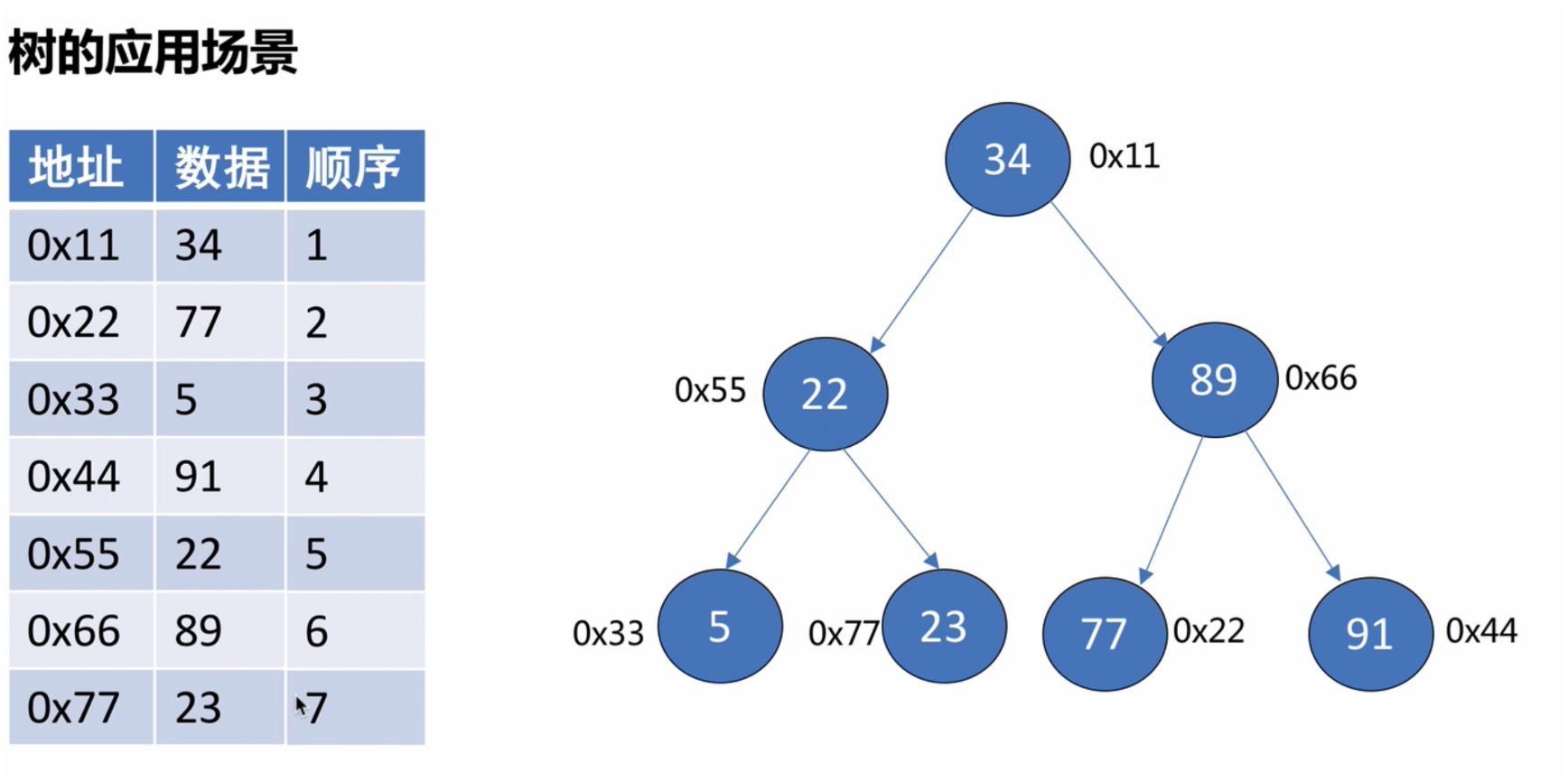
2.6二叉树的概念和性质

2.7广度优先遍历

python 复制代码 
class Node(object):
    """节点类"""
    def __init__(self, item):
        self.item = item
        self.lchild = None
        self.rchild = None


class BinaryTree(object):
    """二叉树"""
    def __init__(self, node=None):
        self.root = node

    def add(self, item):
        """添加节点"""
        pass

    def bradh_travel(self):
        """广度优先遍历"""
        pass
  1. 深度优先遍历：沿着某一个路径遍历到叶子结点，再从另外一个路径遍历，直到遍历完所有的结点
  2. 广度优先遍历：按照层次进行遍历

2.8添加节点思路分析

  1. 初始操作：初始化队列、将根节点入队、创建新结点
  2. 重复执行：
    • 获得并弹出队头元素
      1. 如果当前结点的左右子结点不为空，则将其左右子节点入队
      2. 如果当前结点的左右子节点为空，则将新结点挂到为空的左子结点、或者右子节点

2.9遍历方法的实现

python 复制代码 
class Node(object):
    """节点类"""
    def  __init__(self, item):
        self.item = item
        self.lchild = None
        self.rchild = None


class BinaryTree(object):
    """完全二叉树"""
    def __init__(self, node=None):
        self.root = node

    def add(self, item):
        """添加节点"""
	
  		# 初始操作：初始化队列
        if self.root == None:
            self.root = Node(item)
            return

        # 队列
        queue = []
        # 根节点入队
        queue.append(self.root)
				
        while True:
            # 从头部取出数据
            node = queue.pop(0)
            # 判断左节点是否为空
            if node.lchild == None:
                node.lchild = Node(item)
                return
            else:
                queue.append(node.lchild)

            if node.rchild == None:
                node.rchild = Node(item)
                return
            else:
                queue.append(node.rchild)

	def breadh_travel(self):
        """广度优先遍历"""

        if self.root == None:
            return

        # 队列
        queue = []
        # 添加数据
        queue.append(self.root)

        while len(queue)>0:
            # 取出数据
            node = queue.pop(0)
            print(node.item, end="")

            # 判断左右子节点是否为空
            if node.lchild is not None:
                queue.append(node.lchild)
            if node.rchild is not None:
                queue.append(node.rchild)
if __name__ == '__main__':
    tree = BinaryTree()
    tree.add("A")
    tree.add("B")
    tree.add("C")
    tree.add("D")
    tree.add("E")
    tree.add("F")
    tree.add("G")
    tree.add("H")
    tree.add("I")
    tree.breadh_travel()

A B C D E F G H I

2.10二叉树的三种深度优先遍历

先序遍历：先访问根节点、再访问左子树、最后访问右子树

中序遍历：先访问左子树、再访问根节点、最后访问右子树

后序遍历：先访问左子树、再访问右子树、最后访问根节点

  1. 无论那种遍历方式，都是先访问左子树、再访问右子树
  2. 碰到根节点就输出、碰到左子树、右子树就递归 注意：左子树右子树是一棵树所以递归；根节点是一个节点所以打印输出

2.11二叉树的三种深度优先遍历代码实现

python 复制代码 
class Node(object):
    """节点类"""
    def  __init__(self, item):
        self.item = item
        self.lchild = None
        self.rchild = None


class BinaryTree(object):
    """完全二叉树"""
    def __init__(self, node=None):
        self.root = node

    def add(self, item):
        """添加节点"""

        if self.root == None:
            self.root = Node(item)
            return

        # 队列
        queue = []
        # 从尾部添加数据
        queue.append(self.root)

        while True:
            # 从头部取出数据
            node = queue.pop(0)
            # 判断左节点是否为空
            if node.lchild == None:
                node.lchild = Node(item)
                return
            else:
                queue.append(node.lchild)

            if node.rchild == None:
                node.rchild = Node(item)
                return
            else:
                queue.append(node.rchild)

    def breadh_travel(self):
        """广度优先遍历"""

        if self.root == None:
            return

        # 队列
        queue = []
        # 添加数据
        queue.append(self.root)

        while len(queue)>0:
            # 取出数据
            node = queue.pop(0)
            print(node.item, end="")

            # 判断左右子节点是否为空
            if node.lchild is not None:
                queue.append(node.lchild)
            if node.rchild is not None:
                queue.append(node.rchild)

    def preorder_travel(self, root):
        """先序遍历 根 左 右"""
        if root is not None:
            # 先访问根节点
            print(root.item, end="")
            # 递归再访问左子树
            self.preorder_travel(root.lchild)
            # 递归访问右子树
            self.preorder_travel(root.rchild)

    def inorder_travel(self, root):
        """中序遍历 左 根 右"""
        if root is not None:
            self.inorder_travel(root.lchild)
            print(root.item, end="")
            self.inorder_travel(root.rchild)

    def postorder_travel(self, root):
        """后序遍历 根 左 右"""
        if root is not None:
            self.postorder_travel(root.lchild)
            self.postorder_travel(root.rchild)
            print(root.item, end="")


if __name__ == '__main__':
    tree = BinaryTree()
    tree.add("0")
    tree.add("1")
    tree.add("2")
    tree.add("3")
    tree.add("4")
    tree.add("5")
    tree.add("6")
    tree.add("7")
    tree.add("8")
    tree.add("9")
    tree.preorder_travel(tree.root)
    print()
    tree.inorder_travel(tree.root)
    print()
    tree.postorder_travel(tree.root)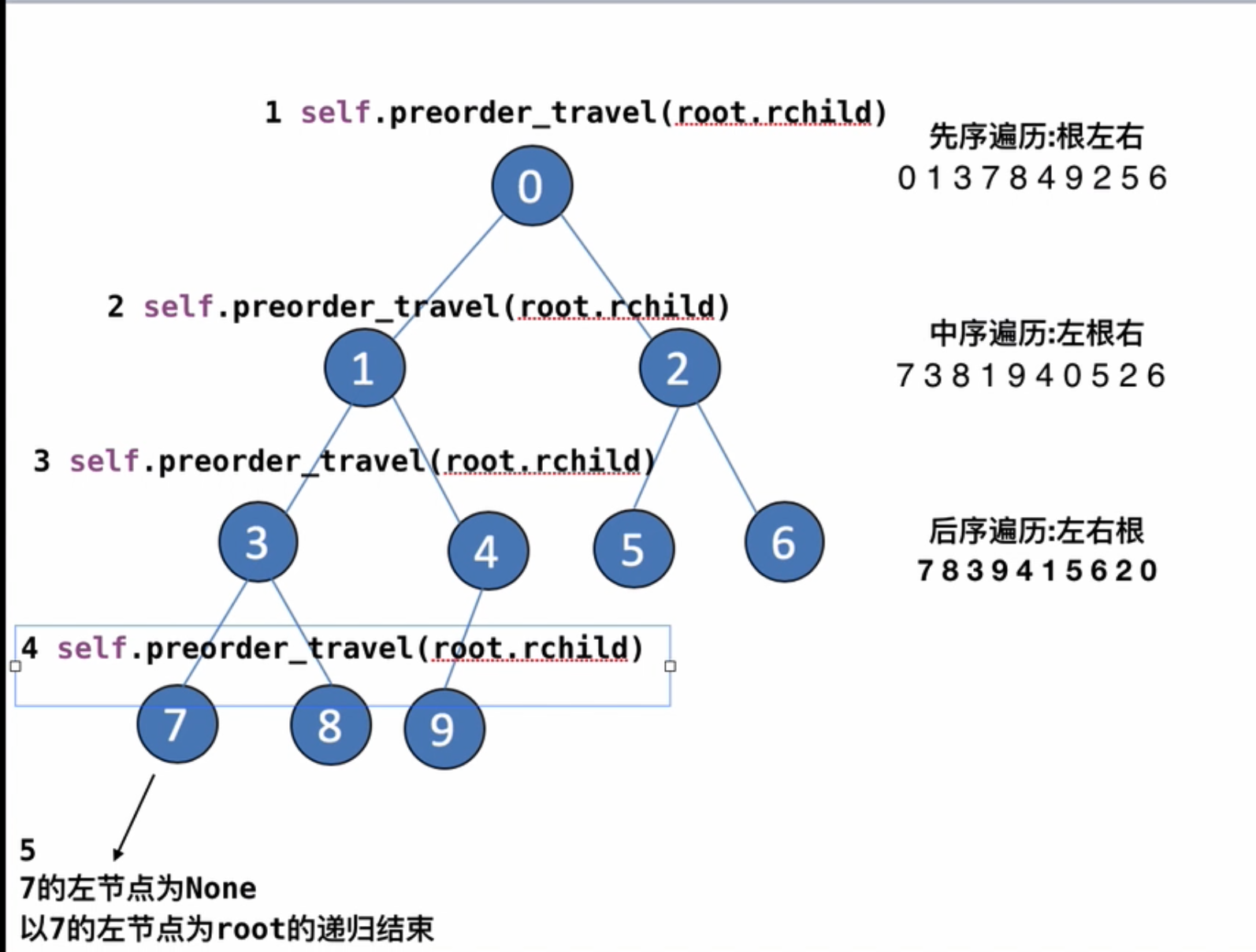

2.12二叉树由遍历结果反推二叉树的结构

我们需要知道先序遍历结果和中序遍历结果、或者后序遍历结果和中序遍历结果才能够确定唯一一棵树。

只知道先序遍历、后序遍历结果，不能保证确定唯一的一棵树。

通过先序遍历可以确定哪个元素是根节点，通过中序遍历可以知道左子树都有那些结点、右子树都有那些结点。

相关推荐
ACERT3332 小时前
1.吴恩达机器学习笔记week1-2（线性回归模型及Sklearn的使用）
人工智能·python·机器学习
感哥3 小时前
Python 异步编程
python
鹤顶红6533 小时前
Python -- 人生重开模拟器（简易版）
服务器·前端·python
刚入坑的新人编程3 小时前
算法训练.15
数据结构·c++·算法·哈希算法
databook3 小时前
Manim实现镜面反射特效
后端·python·动效
星哥说事3 小时前
Python自学21 - Python处理图像
python
西猫雷婶3 小时前
python学智能算法（三十八）|使用Numpy和PyTorch模块绘制正态分布函数图
pytorch·python·numpy
蕓晨3 小时前
循环队列_数组实现
数据结构·c++·算法
2301_764441333 小时前
使用python的加权Jaccard分析流程
开发语言·python
热门推荐
01UV 工具安装与国内镜像源配置指南02Spec-Kit 使用指南03GitHub 镜像站点0446个Nano-banana 精选提示词，持续更新中05UV安装并设置国内源06保姆级教程：手把手教你用Dify实现完美多轮对话（附Chatflow和提示词）07KGG转MP3工具|非KGM文件|解密音频08解决 WSL Ubuntu 中 /etc/resolv.conf 自动重置问题09Linux下V2Ray安装配置指南10jdk21下载、安装（Windows、Linux、macOS）