设计模式第四章(组合模式)

组合模式（Composite Pattern）是一种结构型设计模式 ，核心思想是将对象组合成树形结构，使客户端能以统一的方式处理单个对象和对象的组合。

简单来说，它就像处理 "文件夹和文件" 的逻辑：文件夹（组合对象）可以包含文件（单个对象）或其他文件夹（嵌套组合对象），而用户操作时不需要区分 "点的是文件还是文件夹"------ 无论是删除、复制还是查看大小，都能用同样的方式处理。

核心解决的问题

当系统中存在 **"整体 - 部分" 的树形关系 **（如组织架构、UI 组件树、文件系统等），且希望客户端代码无需区分 "单个元素" 和 "元素组合"时，组合模式可以消除这种差异，简化代码逻辑。

结构组成

组合模式包含 3 个核心角色：

抽象组件（Component）

定义单个对象和组合对象的共同接口（如 "获取名称""计算大小""添加子元素" 等方法），是客户端操作的统一入口。
叶子节点（Leaf）

树形结构中的最小单元，没有子节点（如 "文件""按钮"）。实现抽象组件的接口，但不实现 "添加 / 删除子元素" 等与组合相关的方法（或直接抛出异常）。
复合节点（Composite）

包含子节点的组合对象（如 "文件夹""面板"），可以是叶子节点或其他复合节点。实现抽象组件的所有接口，尤其负责管理子节点（添加、删除、遍历等）。

举个例子：文件系统

抽象组件（Component） ：FileSystemNode，定义方法getName()（获取名称）、getSize()（获取大小）、addChild()（添加子节点）。
叶子节点（Leaf） ：File，实现getName()和getSize()（返回文件本身大小），addChild()直接抛出异常（文件不能包含子元素）。
复合节点（Composite） ：Folder，实现getName()，getSize()返回所有子节点的大小之和，addChild()用于添加文件或子文件夹。

客户端代码可以这样统一操作：

java 复制代码

// 无论是文件还是文件夹，都用同样的方式调用
FileSystemNode file = new File("笔记.txt", 1024);
FileSystemNode folder = new Folder("文档");
folder.addChild(file);

System.out.println(file.getName()); // 单个对象操作
System.out.println(folder.getSize()); // 组合对象操作（自动计算所有子元素大小）

核心优势

客户端简化：无需判断操作的是 "单个元素" 还是 "组合元素"，统一调用接口。
扩展性好：新增叶子节点或复合节点时，无需修改现有代码（符合开闭原则）。
清晰表达树形结构：自然映射 "整体 - 部分" 关系，代码结构与业务逻辑一致。

适用场景

数据结构是树形结构（如组织架构树、菜单树、XML/JSON 节点树）。
希望客户端统一处理单个对象和组合对象（无需区分类型）。

典型案例：GUI 框架中的组件树（面板包含按钮、输入框，或嵌套其他面板）、权限系统中的角色层级（角色包含子角色和权限点）等。

实战部分1

我们需要计算每个省里面有多少人口，该如何计算
- 每个省份里面有多个城市
- 每个城市有很多区域
- 每个区域可以统计人数

这种数据就适用于组合模式，省里面包含城市，城市包含地区

代码部分

人口节点的接口类

java 复制代码

public interface PopulationNode {


    /**
     *  统计人口
     * @return
     */
    int computePopulation();
}

区域，假设这是一个最小的单位

java 复制代码

public class District implements PopulationNode{

    private final String name;

    // 区域的人口
    private int populationNum;

    public District(String name,int populationNum) {
        this.name = name;
        this.populationNum = populationNum;
    }



    @Override
    public int computePopulation() {
        return this.populationNum;
    }
}

城市，里面包含多个区域

java 复制代码

public class City implements PopulationNode{

    private final String name;

    private List<PopulationNode> districtList = new ArrayList<>();


    public void addDistrict(District district) {
        districtList.add(district);
    }

    public City(String name) {
        this.name = name;
    }


    @Override
    public int computePopulation() {
        return districtList.stream().mapToInt(PopulationNode::computePopulation).sum();
    }
}

省份，包含多个城市

java 复制代码

public class Province implements PopulationNode{
    private final String name;

    private List<PopulationNode> cityList = new ArrayList<>();

    public Province(String name) {
        this.name = name;
    }

    public void addCity(City city) {
        cityList.add(city);
    }


    @Override
    public int computePopulation() {
        return this.cityList.stream().mapToInt(PopulationNode::computePopulation).sum();
    }
}

测试部分

java 复制代码

 *
 *   组合模式    树是一个经典的组合模式，自己肚子里面有一堆节点，节点里面继续嵌套一堆节点
 *   我们创建一个 地区，假设这个地区是一个最小单位节点
 *   城市里面包含多个地区
 *   省份里面包含多个城市
 *   实际上我们最终计算的是地区的人口数相加即可得到总人口数
 */
public class TestMain {


    public static void main(String[] args) {
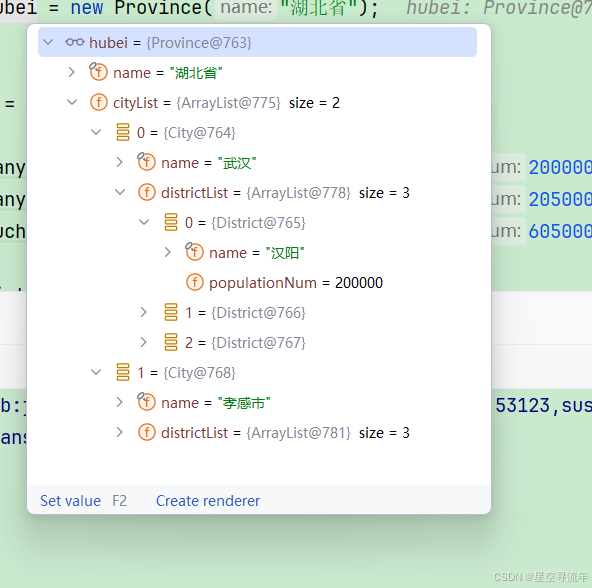
        Province hubei = new Province("湖北省");

        // 城市
        City wuhan = new City("武汉");
        //区域
        District hanyang = new District("汉阳",200000);
        District hanykou = new District("汉口",205000);
        District wuchang = new District("武昌",605000);

        wuhan.addDistrict(hanyang);
        wuhan.addDistrict(hanykou);
        wuhan.addDistrict(wuchang);


        // 城市
        City xiaogan = new City("孝感市");
        //区域
        District dawu = new District("大悟县",20000);
        District xiaochang = new District("孝昌县",25000);
        District yunmeng = new District("云梦",65000);

        xiaogan.addDistrict(dawu);
        xiaogan.addDistrict(xiaochang);
        xiaogan.addDistrict(yunmeng);



        hubei.addCity(wuhan);
        hubei.addCity(xiaogan);

        System.out.println("湖北省总人口数量："+hubei.computePopulation());
        System.out.println("孝感市人口数："+xiaogan.computePopulation());

    }

}

设计一个计算器

暂时只设计一个加法表达式

代码部分

java 复制代码

public interface Expression {


    int getValue();
}


/**
 *  数字类型表达式
 */
class NumberExpression implements Expression {

    private final int value;

    NumberExpression(int value) {
        this.value = value;
    }

    @Override
    public int getValue() {
        return value;
    }
}


/**
 *  加法表达式，  那么 左右个需要一个
 */
class AddExpression implements Expression {

    private final Expression left;
    private final Expression right;

    AddExpression(Expression left, Expression right) {
        this.left = left;
        this.right = right;
    }


    @Override
    public int getValue() {
        return this.left.getValue() + this.right.getValue();
    }
}

测试部分

java 复制代码

public class Calc {


    public static void main(String[] args) {
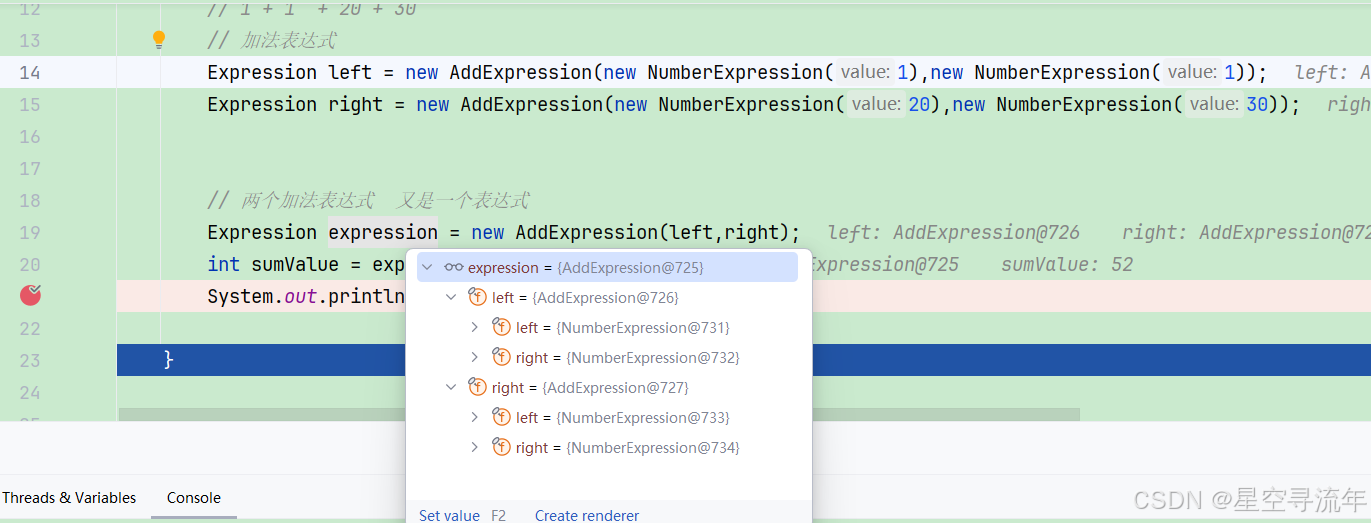
        // 1 + 1  + 20 + 30
        // 加法表达式
        Expression left = new AddExpression(new NumberExpression(1),new NumberExpression(1));
        Expression right = new AddExpression(new NumberExpression(20),new NumberExpression(30));


        // 两个加法表达式  又是一个表达式
        Expression expression = new AddExpression(left,right);
        int sumValue = expression.getValue();
        System.out.println(sumValue);

    }

高版本计算器实现

假设我们的表达式是 1+15*(9+4+(1+5))+6 这种有括号还有算数类的，这种该如何拆分

前言

一、先明确：中缀 vs 后缀表达式

中缀表达式 ：我们日常使用的格式，运算符在两个操作数中间 （如 3 + 4 * 2 - (1 + 5)），需要考虑 "运算符优先级" 和 "括号优先级"，计算时需调整顺序。
后缀表达式（逆波兰表达式） ：运算符在对应操作数的后面 （如 3 4 2 * + 1 5 + -），无需括号和优先级判断，按从左到右顺序即可计算（遇到运算符就用前面两个操作数运算）。

转换的核心目标：消除中缀的优先级和括号依赖，生成能直接按顺序计算的后缀格式。

二、转换的核心规则与工具

1. 必备工具

转换过程需要两个核心 "容器"，可视化图通常分为三部分：

区域 1：中缀表达式（待遍历）	区域 2：运算符栈（暂存运算符）	区域 3：结果列表（生成后缀表达式）
例如：`3 + 4 * 2 - (1 + 5)`	栈顶 → 空（初始状态）	空（初始状态）

运算符栈：用于暂存还未确定位置的运算符，核心作用是 "处理优先级"------ 优先级低的运算符要等优先级高的先进入结果。
结果列表：直接收集操作数和 "符合优先级的运算符"，最终输出就是后缀表达式。

2. 关键优先级定义（必须先明确）

转换时需遵循 "运算符优先级"，默认规则（优先级从高到低）：

括号：( 优先级最低（仅用于标记分组，不参与运算顺序）；) 不进栈，仅触发括号内运算符出栈。
乘除：*、/ 优先级高（同一级别）。
加减：+、- 优先级低（同一级别）。

三、转换的核心总结（关键记忆点）

操作数：见一个，直接丢进结果列表（无需判断）。
运算符：比栈顶 "小或等" 就弹栈（按优先级），弹到能进栈为止；栈空直接进。
括号：( 直接进栈，) 弹栈到 ( 为止（( 丢弃）。
最后一步：中缀遍历完，把栈里剩下的运算符全弹进结果。

按这个逻辑，无论多复杂的中缀表达式（带多层括号、不同优先级），都能一步步转成后缀格式，后续计算时只需按后缀顺序 "遇运算符就用前两个数运算" 即可。

代码部分

抽象父类

java 复制代码

public interface Expression {


    int getValue();

}

数字表达式类

java 复制代码

public class NumberExpression implements Expression{

    private final int value;

    public NumberExpression(int value) {
        this.value = value;
    }


    @Override
    public int getValue() {
        return this.value;
    }
}

数字操作类

java 复制代码

public abstract class BinaryOperatorExpression implements Expression{

    protected Expression left;
    protected Expression right;


    protected BinaryOperatorExpression(Expression left,Expression right) {
        this.left = left;
        this.right = right;
    }

}

算术类

加法表达式

java 复制代码

public class AddExpression extends BinaryOperatorExpression {


    public AddExpression(Expression left, Expression right) {
        super(left, right);
    }

    @Override
    public int getValue() {
        return left.getValue() + right.getValue();
    }
}

减法操作类

java 复制代码

public class SubtractionExpression extends BinaryOperatorExpression {


    public SubtractionExpression(Expression left, Expression right) {
        super(left, right);
    }

    @Override
    public int getValue() {
        return left.getValue() - right.getValue();
    }
}

乘法操作类

java 复制代码

public class MultiplicationExpression extends BinaryOperatorExpression {


    public MultiplicationExpression(Expression left, Expression right) {
        super(left, right);
    }

    @Override
    public int getValue() {
        return left.getValue() * right.getValue();
    }
}

除法操作类

java 复制代码

public class DivisionExpression extends BinaryOperatorExpression {


    public DivisionExpression(Expression left, Expression right) {
        super(left, right);
    }

    @Override
    public int getValue() {
        return left.getValue() / right.getValue();
    }
}

解析类

中缀表达式转为后缀表达式
后缀表达式计算结果

中缀表达式转为后缀表达式

java 复制代码

public class ExpressionParser {


    // 中缀表达式  (1 + 2) * 3 + (4 + 6)
    private final String middleExpression;

    // 指针指向的位置
    int point = 0;


    public ExpressionParser(String middleExpression) {
        this.middleExpression = middleExpression;
    }


    /**
     *  转为后缀表达式
     * @return
     */
    public List<String> toSuffix() {
        // 最终返回的后缀表达式
        List<String> subffixList = new ArrayList<>();

        // 辅助栈
        LinkedList<String> assistStack = new LinkedList<>();

        while (point < middleExpression.length()) {
            // 拿到的字符
            char c = middleExpression.charAt(point);

            // 左括号
            if (c == '(') {
                // 入辅助栈
                assistStack.addLast(c+"");
            } else if (c == ')') {
                // 右括号，遍历元素，直到遇到左括号，然后消除这一对括号
                while (!assistStack.getLast().equals("(")) {
                    subffixList.add(assistStack.removeLast());
                }
                assistStack.removeLast();
            } else if (c == '*' || c == '/') {
                while (!assistStack.isEmpty() && (assistStack.getLast().equals("*") || assistStack.getLast().equals("/"))) {
                    subffixList.add(assistStack.removeLast());
                }
                assistStack.addLast(c+"");
            } else if (c == '+' || c == '-') {
                while (topIsOperator(assistStack)) {
                    subffixList.add(assistStack.removeLast());
                }
                assistStack.addLast(c + "");
            } else if (Character.isDigit(c)) {
                StringBuilder numStr = new StringBuilder();
                while (point < middleExpression.length() && Character.isDigit(middleExpression.charAt(point))) {
                    numStr.append(middleExpression.charAt(point));
                    point ++;
                }
                point --;
                subffixList.add(numStr.toString());
            } else {
                throw new IllegalArgumentException("非法的操作符");
            }
            point ++;
        }

        while (!assistStack.isEmpty()) {
            subffixList.add(assistStack.removeLast());
        }

        return subffixList;
    }


    private boolean topIsOperator(LinkedList<String> assistStack) {
        if (assistStack.isEmpty()) {
            return false;
        }

        return Set.of("+","-","*","/").contains(assistStack.getLast());
    }
}

后缀表达式计算

后缀表达式（逆波兰表达式）的计算逻辑非常直观，核心依赖栈（先进后出） 暂存操作数，整体遵循 "从左到右遍历，遇操作数入栈，遇运算符则取栈顶操作数计算" 的规则，无需考虑优先级或括号（这些在转换为后缀时已处理）。

java 复制代码

    public Expression parse() {
        List<String> suffixList = this.toSuffix();
        LinkedList<Expression> stack = new LinkedList<>();

        for (String item : suffixList) {
            if (item.equals("+")) {
                Expression right = stack.removeLast();
                stack.addLast(new AddExpression(stack.removeLast(),right));
            } else if (item.equals("-")) {
                Expression right = stack.removeLast();
                stack.addLast(new SubtractionExpression(stack.removeLast(),right));
            } else if (item.equals("*")) {
                Expression right = stack.removeLast();
                stack.addLast(new MultiplicationExpression(stack.removeLast(),right));
            } else if (item.equals("/")) {
                Expression right = stack.removeLast();
                stack.addLast(new DivisionExpression(stack.removeLast(),right));
            } else {
                int num = Integer.parseInt(item);
                stack.addLast(new NumberExpression(num));
            }
        }
        return stack.getLast();
    }

测试用例

java 复制代码

public class MainTest {

    public static void main(String[] args) {
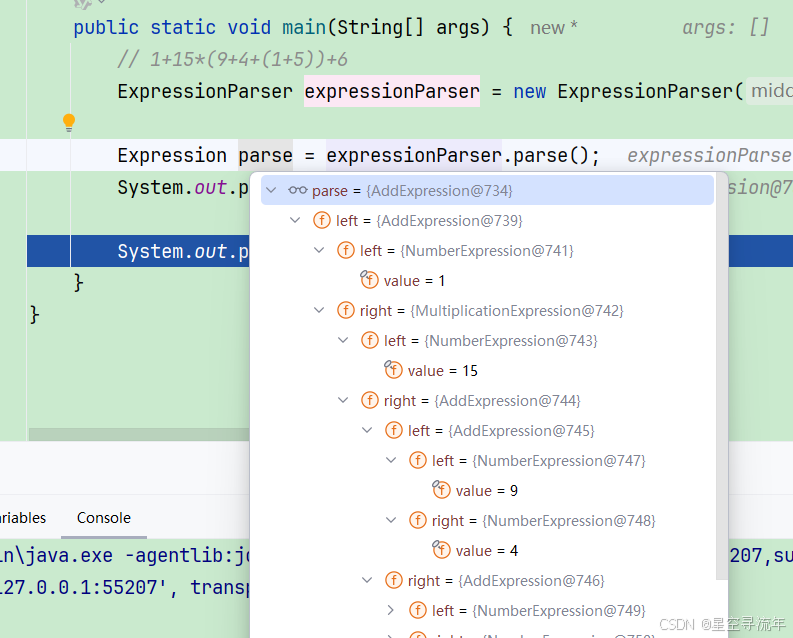
        // 1+15*(9+4+(1+5))+6
        ExpressionParser expressionParser = new ExpressionParser("1+15*(9+4+(1+5))+6");

        Expression parse = expressionParser.parse();
        System.out.println(parse.getValue());

        System.out.println(1+15*(9+4+(1+5))+6);
    }
}

最终计算结果 292