GESP C++5级 2025年6月编程2题解：最大公因数

P13014 [GESP202506 五级] 最大公因数

题目描述

对于两个正整数 a,ba,ba,b，他们的最大公因数记为 gcd⁡(a,b)\gcd(a,b)gcd(a,b)。对于 k>3k > 3k>3 个正整数 c1,c2,...,ckc_1,c_2,\dots,c_kc1,c2,...,ck，他们的最大公因数为：

gcd⁡(c1,c2,...,ck)=gcd⁡(gcd⁡(c1,c2,...,ck−1),ck)\gcd(c_1,c_2,\dots,c_k)=\gcd(\gcd(c_1,c_2,\dots,c_{k-1}),c_k)gcd(c1,c2,...,ck)=gcd(gcd(c1,c2,...,ck−1),ck)

给定 nnn 个正整数 a1,a2,...,ana_1,a_2,\dots,a_na1,a2,...,an 以及 qqq 组询问。对于第 i(1≤i≤q)i(1 \le i \le q)i(1≤i≤q) 组询问，请求出 a1+i,a2+i,...,an+ia_1+i,a_2+i,\dots,a_n+ia1+i,a2+i,...,an+i 的最大公因数，也即 gcd⁡(a1+i,a2+i,...,an+i)\gcd(a_1+i,a_2+i,\dots,a_n+i)gcd(a1+i,a2+i,...,an+i)。

输入格式

第一行，两个正整数 n,qn,qn,q，分别表示给定正整数的数量，以及询问组数。

第二行，nnn 个正整数 a1,a2,...,ana_1,a_2,\dots,a_na1,a2,...,an。

输出格式

输出共 qqq 行，第 iii 行包含一个正整数，表示 a1+i,a2+i,...,an+ia_1+i,a_2+i,\dots,a_n+ia1+i,a2+i,...,an+i 的最大公因数。

输入输出样例 #1

输入 #1

5 3
6 9 12 18 30

输出 #1

1
1
3

输入输出样例 #2

输入 #2

3 5
31 47 59

输出 #2

4
1
2
1
4

说明/提示

对于 60%60\%60% 的测试点，保证 1≤n≤1031 \le n \le 10^31≤n≤103，1≤q≤101 \le q \le 101≤q≤10。

对于所有测试点，保证 1≤n≤1051 \le n \le 10^51≤n≤105，1≤q≤1051 \le q \le 10^51≤q≤105，1≤ai≤10001 \le a_i \le 10001≤ai≤1000。

题目大意

给定nnn个正整数组成的序列aaa和qqq次询问，对于第i(1≤i≤q)i(1\le i\le q)i(1≤i≤q)次询问，输出gcd⁡(a1+i,a2+i,...,an+i)\gcd(a_1+i,a_2+i,\dots,a_n+i)gcd(a1+i,a2+i,...,an+i)的值。

题目分析

先说TLE的解法。

最简单的办法就是在输入后直接一次一次反复求整个数组加iii的最大公因数，意思就是直接处理每次询问，每次询问都遍历数组且求一遍gcd⁡\gcdgcd，这是很多考生都用的办法。

欧几里得算法模板

欧几里得算法（辗转相除法）求最大公因数可以用下面的精简代码

int gcd(int x,int y)
{
	return y==0?x:gcd(y,x%y);
}

也可以使用迭代

int gcd(int x,int y)
{
	while(y!=0)
	{
		int tmp=y;
		y=x%y;
		x=tmp;
	}
	return x;
}

复杂度如下表

	递归	迭代
时间复杂度	O(log⁡n)O(\log n)O(logn)	O(log⁡n)O(\log n)O(logn)
空间复杂度	O(log⁡n)O(\log n)O(logn)	O(1)O(1)O(1)

递归的空间用于递归栈调用，该题中无需考虑。

TLE Code

#include<bits/stdc++.h>
using namespace std;
int a[100001];
int gcd(int x,int y)
{
	return y==0?x:gcd(y,x%y);
}
int main()
{
	int n,q;
	cin>>n>>q;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=1;i<=q;i++)
	{
		int g=a[1]+i;
		for(int j=2;j<=n;j++)g=gcd(g,a[j]+i);
		cout<<g<<endl;
	}
	return 0;
}

但是一旦提交

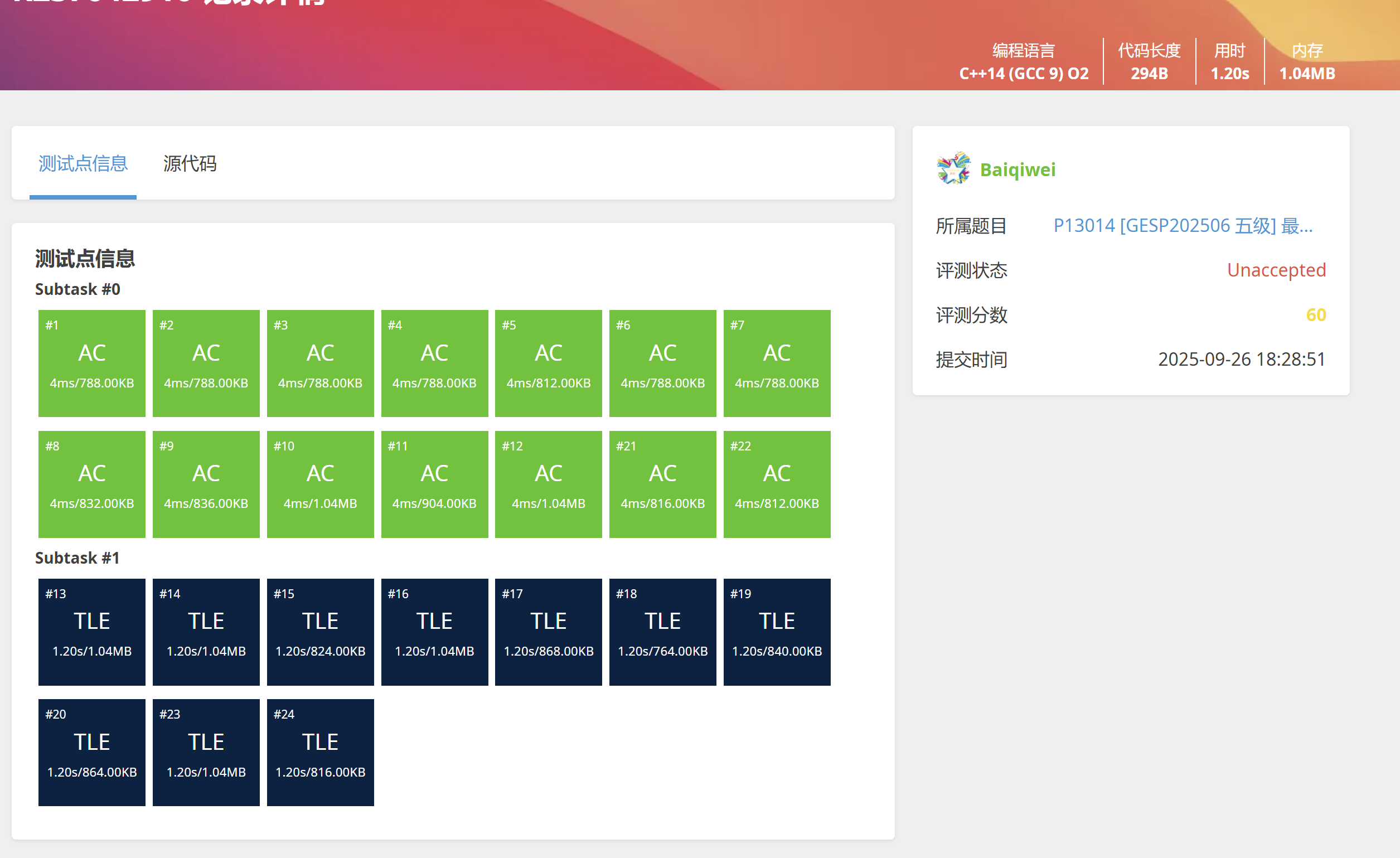
就噶了。

TLE Time

输入比处理快，只看处理部分。

外重循环：O(q)O(q)O(q)

内重循环：O(n)O(n)O(n)
gcd⁡\gcdgcd：O(log⁡ai)O(\log a_i)O(logai)

总时间：O(nqlog⁡ai)O(nq\log a_i)O(nqlogai)，数据范围不让过。

那过的方法是什么呢？

差分数组

对于长度为nnn的序列aaa，他的差分数组第一项与原数组第一项相等，后面差分数组第i(2≤i≤n)i(2\le i\le n)i(2≤i≤n)项等于ai−ai−1a_i-a_{i-1}ai−ai−1，注意即使是负数也不能绝对值。

现在，我要证明一个东西：gcd⁡(a+c,b+c)=gcd⁡(a+c,b−a)\gcd(a+c,b+c)=\gcd(a+c,b-a)gcd(a+c,b+c)=gcd(a+c,b−a)

证明gcd⁡(a+c,b+c)=gcd⁡(a+c,b−a)\gcd(a+c,b+c)=\gcd(a+c,b-a)gcd(a+c,b+c)=gcd(a+c,b−a)

众所周知，辗转相除法一开始是辗转相减法，后来通过优化才变成辗转相除法。

后面的取模比之前的相减快多了，但是不要忘本。

对于gcd(a,b)，可以推出gcd(b,a-b)，他们是等价的，你可以想象成在一个大长方形里面取截取最大的正方形，剩下的长宽就是gcd的参数。

那么用于gcd⁡(a+c,b+c)=gcd⁡(a+c,b−a)\gcd(a+c,b+c)=\gcd(a+c,b-a)gcd(a+c,b+c)=gcd(a+c,b−a)也好使，就假设a+ca+ca+c是a′a'a′，b+cb+cb+c是b′b'b′：
gcd⁡(a′,b′)=gcd⁡(a′,b−a)\gcd(a',b')=\gcd(a',b-a)gcd(a′,b′)=gcd(a′,b−a)。你感觉不一样。

来，别急，aaa和bbb的大小关系是要调整的，gcd⁡(a′,b−a)\gcd(a',b-a)gcd(a′,b−a)变成gcd⁡(b′,a−b)\gcd(b',a-b)gcd(b′,a−b)，是不是恍然大悟了？

没错，跟辗转相减法几乎一样了。其实这个式子是gcd⁡(a,b)\gcd(a,b)gcd(a,b)演变而来，他就是把a,ba,ba,b都加上ccc，证明新aaa和a,ba,ba,b差的最大公因数就是新的两个数的最大公因数。

这样，就能在一串数中，整体递增相同元素后快速找到最大公因数。

没听懂证明过程？举个栗子！

举个栗子

例如3 7，c=1c=1c=1，gcd⁡(a+c,b+c)=gcd⁡(4,8)=4\gcd(a+c,b+c)=\gcd(4,8)=4gcd(a+c,b+c)=gcd(4,8)=4，gcd⁡(a+c,b−a)=gcd⁡(4,4)=4\gcd(a+c,b-a)=\gcd(4,4)=4gcd(a+c,b−a)=gcd(4,4)=4，确实相等。

再比如5 6，c=2c=2c=2，gcd⁡(a+c,b+c)=gcd⁡(7,8)=1\gcd(a+c,b+c)=\gcd(7,8)=1gcd(a+c,b+c)=gcd(7,8)=1，gcd⁡(a+c,b−a)=gcd⁡(7,1)=1\gcd(a+c,b-a)=\gcd(7,1)=1gcd(a+c,b−a)=gcd(7,1)=1，确实相等。

其实这是必然的，自己随便写几个样例都是的。

实际应用

在一串数中，求完差分数组，把他从第二项起，每一项都取最大公因数。最后在每次询问中，用任意一个元素加上iii再与前面的gcd⁡\gcdgcd结果再一次进行gcd⁡\gcdgcd，得到的结果就是输出的答案。

Code

#include<bits/stdc++.h>
using namespace std;
int a[100001],cf[100001]; //原数组和差分数组
int gcd(int x,int y) //最大公因数
{
	return y==0:x:gcd(y,x%y);
}
int main()
{
	int n,q;
	cin>>n>>q; //输入
	for(int i=1;i<=n;i++)cin>>a[i],cf[i]=a[i]-a[i-1]; //输入 计算差分
	int g=cf[2];
	for(int i=3;i<=n;i++)g=gcd(g,cf[i]); //求gcd
	for(int i=1;i<=q;i++)
	{
		cout<<gcd(a[1]+i,g)<<endl; //处理 输出
	}
	return 0;
}

然而提交的时候

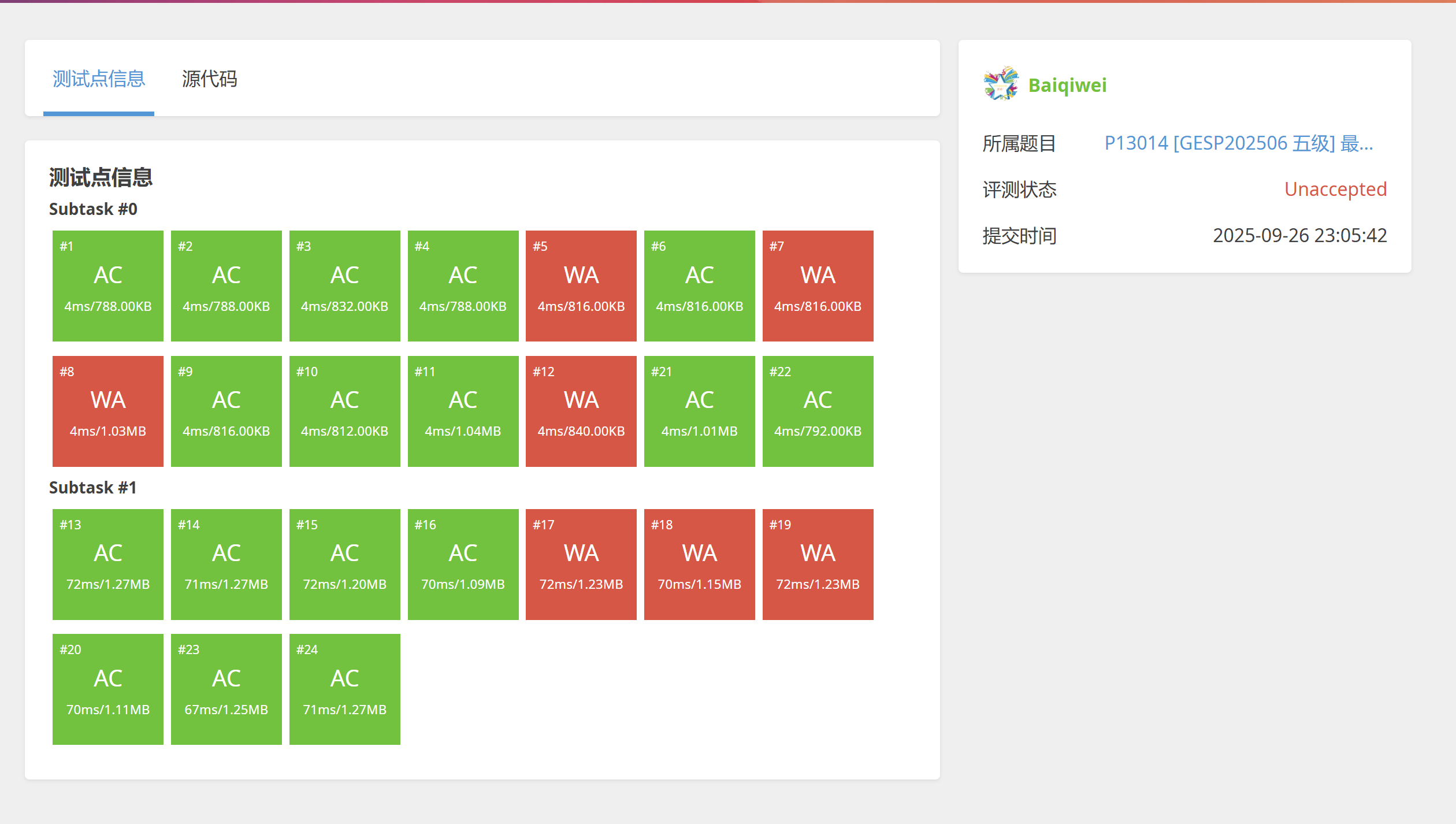
没错，n=1n=1n=1时忘了特判，加了特判能AC。

#include<bits/stdc++.h>
using namespace std;
int a[100001],cf[100001]; //原数组和差分数组
int gcd(int x,int y) //最大公因数
{
	return y==0?x:gcd(y,x%y);
}
int main()
{
	int n,q;
	cin>>n>>q; //输入
	for(int i=1;i<=n;i++)cin>>a[i],cf[i]=a[i]-a[i-1]; //输入 计算差分
    if(n==1)
    {
        for(int i=1;i<=q;i++)cout<<a[1]+i<<endl;
        return 0;
    }
	int g=cf[2];
	for(int i=3;i<=n;i++)g=gcd(g,cf[i]); //求gcd
	for(int i=1;i<=q;i++)
	{
		cout<<gcd(a[1]+i,g)<<endl; //处理 输出
	}
	return 0;
}

...个毛啊！

等一下，0分！？自定义评分脚本这么BT吗？

你一不小心把鼠标放到了wa的点上。

翻译：第3行第一列有字符错误，读取到了-，正确应是1

哦哦哦！忘记处理负数，加个abs就好了！

#include<bits/stdc++.h>
using namespace std;
int a[100001],cf[100001]; //原数组和差分数组
int gcd(int x,int y) //最大公因数
{
	return y==0?x:gcd(y,x%y);
}
int main()
{
	int n,q;
	cin>>n>>q; //输入
	for(int i=1;i<=n;i++)cin>>a[i],cf[i]=a[i]-a[i-1]; //输入 计算差分
    if(n==1)
    {
        for(int i=1;i<=q;i++)cout<<a[1]+i<<endl;
        return 0;
    }
	int g=cf[2];
	for(int i=3;i<=n;i++)g=gcd(g,cf[i]); //求gcd
	for(int i=1;i<=q;i++)
	{
		cout<<abs(gcd(a[1]+i,g))<<endl; //处理 输出
	}
	return 0;
}

啊！终于AC了。

总结

本题对于不会数学的人来说，送你一个词：天方夜谭。

对于只会简单gcd而不知道其中原理而tle的人，送你一个词：一瓶子不满半瓶子晃。

只有会进行细致数学分析和耐心查错的人，才能AC。
为什么5级都是这种数学分析题啊？