数据结构(长期更新)第1讲:
算法复杂度
++跟着潼心走,轻松拿捏C语言,困惑通通走,一去不回头~欢迎开始今天的学++  ++习内容,你的支持就是博主最大的动力++ 。
++习内容,你的支持就是博主最大的动力++ 。 博主主页:潼心1412o-CSDN博客
博主主页:潼心1412o-CSDN博客
目录
[1.1 数据结构前言](#1.1 数据结构前言)
[1.1.1 数据结构](#1.1.1 数据结构)
[1.1.2 算法](#1.1.2 算法)
[1.2 算法效率与复杂度](#1.2 算法效率与复杂度)
[1.3 时间复杂度](#1.3 时间复杂度)
[1.3.1 大O的渐进表示法](#1.3.1 大O的渐进表示法)
[1.3.2 时间复杂度计算实例](#1.3.2 时间复杂度计算实例)
1.1 数据结构前言
1.1.1 数据结构
数据结构(Data Structure)是计算机存储、组织数据的方式
指相互之间存在一种或多种特定关系的数据元素的集合
没有一种单一的数据结构对所有用途都有用,所以要学习各种各样的数据结构
1.1.2 算法
算法(Algorithm)就是定义良好的计算过程
取一个或一组值作为输入,产生一个或一组值输出
简单来讲,就是一系列计算步骤,用来将输入数据转化为输出数据
1.2 算法效率与复杂度
如何衡量算法的好坏(效率高低)
这就要引入复杂度的概念了
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源
因此衡量算法好坏,可从时间空间两个维度考量,及时间复杂度和空间复杂度
时间复杂度主要衡量算法的运行快慢,空间复杂度衡量算法运行时需要的额外时间
一般情况下,时间复杂度的重要性要大于空间复杂度
1.3 时间复杂度
定义:算法的时间复杂度是一个函数式T(N),描述了算法的运行时间
时间算法复杂度是衡量程序的时间效率,为什么不计算程序的运行时间呢
因为程序的运行时间会收到很多因素的影响
1.运行时间与编译环境和运行机器的配置有关系
2.时间只能写好程序后测试,不能在写程序之前通过理论思想进行计算评估
那么我们的做法是
程序执行的时间==二进制指令运行时间(假定每条指令执行时间相同)*执行次数

T(N)==N*N+2N+10
当N不断变⼤时T(N)的差别,上⾯我们已经看到了当N不断变⼤时常数和低阶项对结果的影响很⼩,所以我们只需要计算程序能代表增⻓量级的⼤概执⾏次数,复杂度的表⽰通常使⽤⼤O的渐进表⽰法。
1.3.1 大O的渐进表示法
大O符号(Big O Notation):用于描述函数渐进行为的数学符号
推导大O阶规则
1
|------------------------------------------|
| 时间复杂度函数式T(N)中,只保留最⾼阶项,去掉那些低阶项,因为当N不断变⼤时, |
| 低阶项对结果影响越来越⼩,当N⽆穷⼤时,就可以忽略不计了。 |
|-----------------------------------------|
| 如果最⾼阶项存在且不是1,则去除这个项⽬的常数系数,因为当N不断变⼤,这个系数 |
| 对结果影响越来越⼩,当N⽆穷⼤时,就可以忽略不计了。 |
- T(N)中如果没有N相关的项⽬,只有常数项,⽤常数1取代所有加法常数。
通过以上⽅法,可以得到 Func1 的时间复杂度为: O(N2)
1.3.2 时间复杂度计算实例

T(N)==2N+10
时间复杂度为O(N)

分情况讨论
1.M==N O(M)/O(N)
2.M>>N O(M)
3.M<<N O(N)

T(N)==100
时间复杂度为O(1)
1表示常数量级

1)若要查找的字符在字符串第⼀个位置,则: T (N) = 1
2)若要查找的字符在字符串最后的⼀个位置,则: T (N) = N
3)若要查找的字符在字符串中间位置,则: T (N) =N/2
因此:strchr的时间复杂度分为:
最好情况: O(1)
最坏情况: O(N)
平均情况: O(N)
总结
通过上⾯我们会发现,有些算法的时间复杂度存在最好、平均和最坏情况。
最坏情况:任意输⼊规模的最⼤运⾏次数(上界)
平均情况:任意输⼊规模的期望运⾏次数
最好情况:任意输⼊规模的最⼩运⾏次数(下界)
大O的渐进表示法在实际中⼀般情况关注的是算法的上界,也就是最坏运行情况。
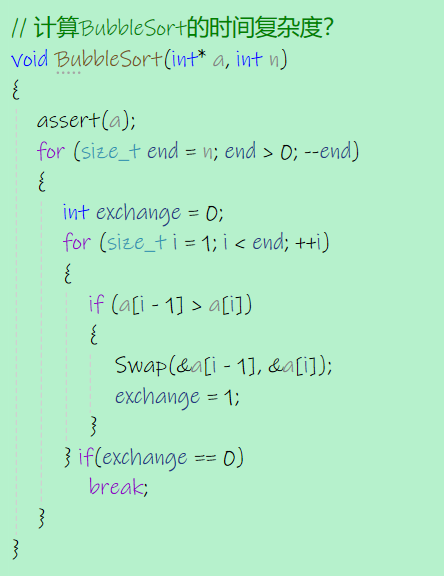
外层循环 内层循环
第一次: n-1
第二次: n-2
第三次: n-3
。。。 。。。
第n次 1
T(N)==1+2+3+...+n-1==n^2/2+n/2
所以时间复杂度为O(N^2)
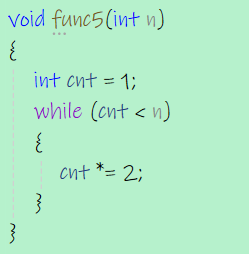
n-2,cnt=2,执行了1次
n=4,cnt=2,4,执行了2次
n=8,cnt=2,4,8,执行了3次
我们发现假设执行次数为x,2^x=n
所以时间复杂度为 O(log2(n))
注意书籍中 log2(n) 、 log n 、 lg n 的表示
当n接近⽆穷⼤时,底数的⼤⼩对结果影响不⼤。因此,⼀般情况下不管底数是多少都可以省略不写,即可以表示为 log n
不同书籍的表示⽅式不同,以上写法差别不⼤,我们建议使⽤ log n

递归算法的时间复杂度==单词递归的时间复杂度*递归次数==1*N
即O(N)
++好了今天的学习内容就到这里啦,谢谢你的陪伴,我是潼心,下次再见~如果这篇文章对你有帮助的话。请务必给主播一个一键三连,球球了,这对主播很重要~++ 
博主主页:潼心1412o-CSDN博客