【机器学习】监督学习 —— 决策树（Decision Tree）

[决策树（Decision Tree）](#决策树（Decision Tree）)

Decision Trees（DT）是一种 非参数的监督学习方法 ，用于 分类和回归 。其目标是通过学习从 数据特征 推断出的 简单决策规则 ，创建一个能够 预测目标变量取值 的模型。

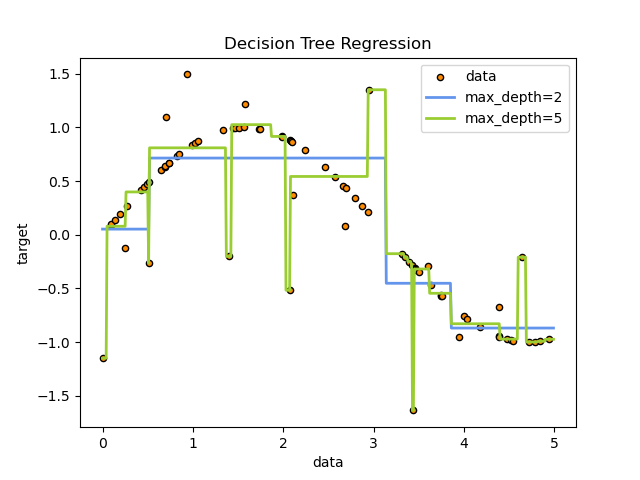
决策树可以视为一种 分段常数近似。

例如，在下方的示例中，决策树通过从数据中学习，以一系列 if‑then‑else 决策规则 来逼近正弦曲线。树的深度越大，决策规则越复杂，模型的拟合程度也越高。

Decision Tree
What is a decision tree?
Decision tree implementation
Decision Trees

决策树（Decision Tree）

决策树通过绘制 不同的选择及其可能的结果 帮助我们做决定。它在机器学习中用于 分类和预测 等任务。

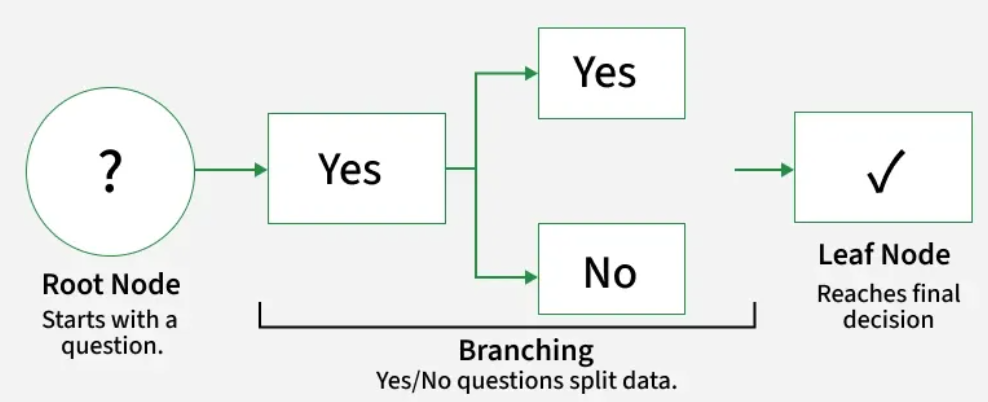
决策树通过展示 不同的选项及其相互关联 帮助我们做决定。它具有 类似树状的结构 ，从称为 根节点 的主要问题开始，根节点代表整个数据集 。随后，树根据数据中的特征 分支出不同的可能性。

它通过不断地对 数据特征 进行分裂，把 样本划分为更小的子集 ，直到 子集尽量"纯" （即大多数样本属于同一类，或 预测值稳定）。

根节点 ：表示 整个数据集的起始点。
分支：连接节点的线条，显示 从一个决策到另一个决策的流程。
内部节点 ：根据数据特征 做出决策的点。
叶节点 ：树的终点，进行 最终决策或预测 的地方。

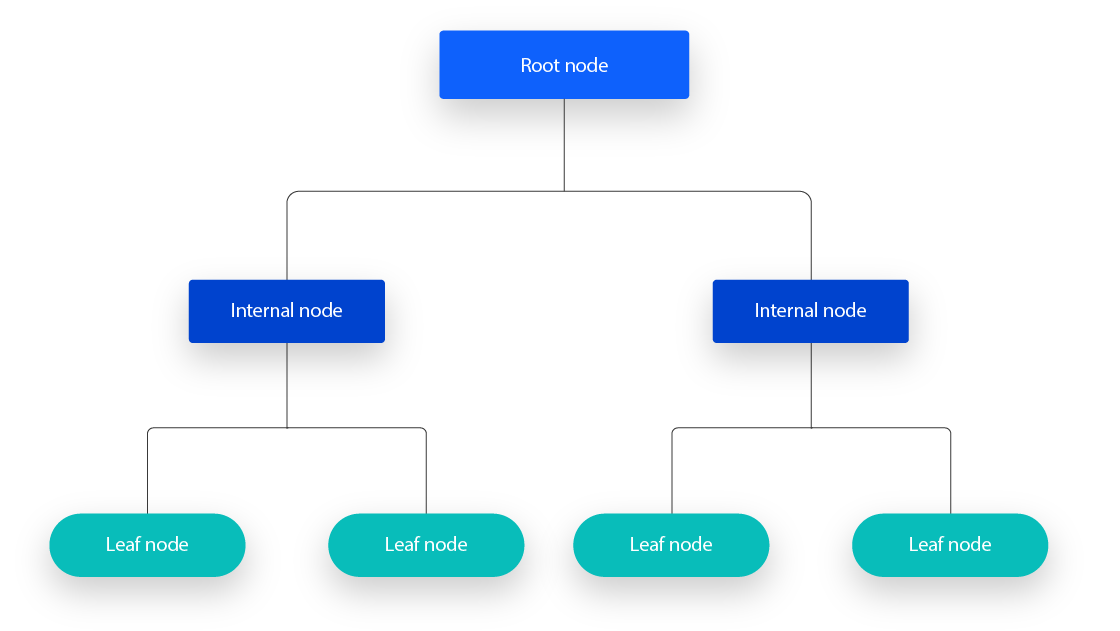
决策树通过递归地 将数据划分为越来越小的子集 来创建。在每一次划分时，数据会依据特定特征进行分割，且分割方式旨在 最大化信息增益。

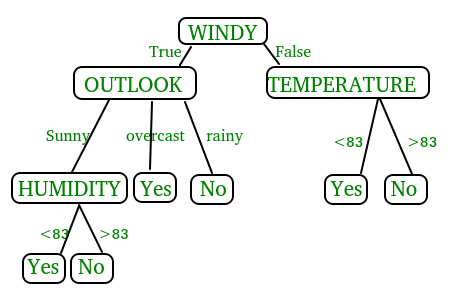
在上图中，决策树是一种类似流程图的树形结构，用于做出决策。它由 根节点 （WINDY）、内部节点 （OUTLOOK、TEMPERATURE）组成，根节点代表 完整的数据集 ，内部节点代表 对属性的测试 ，叶节点 代表 最终决策。树的分支代表测试的可能结果。

决策树分类

根据 目标变量，决策树主要分为两种类型：

分类树 ：用于 预测类别型结果 ，如垃圾邮件或非垃圾邮件等。这类树根据特征 划分数据，以将数据归类到预定义的类别中。
回归树 ：用于 预测连续结果 ，如预测房价。它不进行类别划分，而是根据输入特征提供 数值预测。

根据 划分准则，有以下类型：

ID3 ：Iterative Dichotomiser 3，Quinlan 开发，该算法利用 熵和信息增益 作为度量指标来评估候选划分。
C4.5 ：该算法被视为 ID3 的后续迭代，同样由 Quinlan 开发。它可以使用 信息增益或增益率 来评估决策树中的划分点。
CART ：classification and regression trees，由 Leo Breiman 引入。该算法通常使用 基尼不纯度 （Gini impurity）来确定最佳的划分属性。基尼不纯度衡量随机选择的属性被错误分类的概率。使用基尼不纯度进行评估时，数值越低越理想。

应用场景：

客户流失预测：公司使用决策树根据行为模式、购买历史和互动来预测客户是会离开还是留下。这使企业能够采取主动措施保留客户。

银行贷款审批：银行使用决策树来评估是否应批准贷款申请。决策依据信用评分、收入、就业状况和贷款历史等因素。这样可以预测批准或拒绝，从而实现快速且可靠的决策。

举个例子，假设你正在评估是否应该去冲浪，可以使用以下决策规则来做出选择：

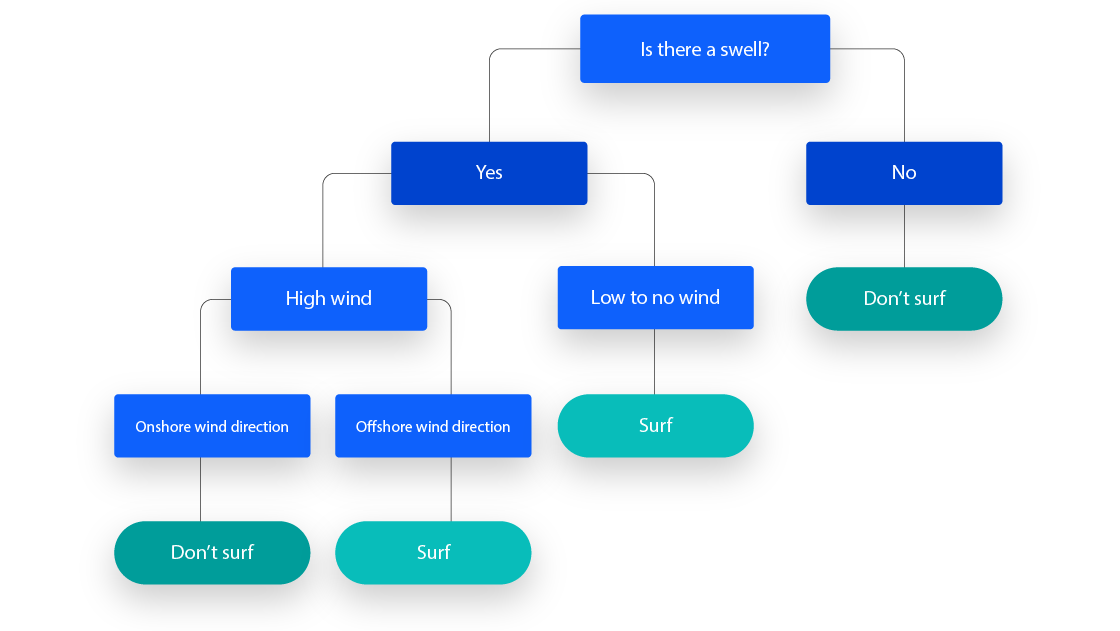
决策树学习采用 分而治之 的策略，通过 贪心搜索 来 确定树中的最佳划分点 。随后，这一划分过程会以 自上而下、递归的方式重复进行，直至所有记录或大多数记录被归入特定的类别标签。

决策树中的划分准则

在决策树中，每个节点的数据划分过程至关重要。划分准则用于 寻找最佳特征 来划分数据，常见的划分准则包括 信息熵 和 基尼不纯度。

熵：它 衡量数据中的不确定性或混乱程度 。决策树通过在提供关于目标变量最多信息的特征上划分数据，以 降低熵。
基尼不纯度 ：该标准 衡量节点的"杂质"程度 。基尼不纯度越低，特征对数据的划分就越能将其分成明确的类别。

这些标准帮助决定在树的每个决策点上，哪些特征对实现最佳划分有用。

熵与信息增益

熵（Entropy）是信息论中的一个概念，最初由香农提出，用来衡量 信息的不确定性 或 混乱程度 。在机器学习的决策树中，熵被引入来度量一个 数据集的纯度（impurity）。

它由以下公式定义，其中：
Entropy ( S ) = − ∑ c ∈ C p ( c ) log ⁡ 2 p ( c ) \text{Entropy}(S) = - \sum_{c \in C} p(c) \log_2 p(c) Entropy(S)=−c∈C∑p(c)log2p(c)

S S S 表示用于 计算熵的数据集 ， c c c 表示集合 S S S 中的类别， C C C 是类别集合，p ( c ) p(c) p(c) 表示属于类别 c c c 的数据点相对于集合 S S S 中总数据点数的比例。

熵值可以在 0 0 0 到 1 1 1 之间。为了选择最佳的划分特征并找到最优决策树，应使用熵最小的属性。

当 所有样本都属于同一类时： p ( c ) = 1 p(c)=1 p(c)=1 ，其他类别概率为 0 0 0，此时熵 = 0 0 0，表示 完全纯净；
当 样本类别均匀分布时 （如二分类时各占 50%）：熵达到最大值 （= 1 1 1），表示 最混乱。

信息增益 表示在 对给定属性进行划分前后熵的差值 。信息增益越大，说明该特征带来的 分类纯度提升越大，因此更适合用于划分。。信息增益通常用以下公式表示，

Information Gain ( S , A ) = Entropy ( S ) − ∑ v ∈ values(A) ∣ S v ∣ ∣ S ∣ Entropy ( S v ) \text{Information\ Gain}(S, A) = \text{Entropy}(S) - \sum_{v \in \text{values(A)}} \frac{| S_v |}{| S| } \text{Entropy}(S_v) Information Gain(S,A)=Entropy(S)−v∈values(A)∑∣S∣∣Sv∣Entropy(Sv)

其中，A A A 代表一个特定的属性或类标签 ， Entropy ( S ) \text{Entropy}(S) Entropy(S) 是数据集 S S S 的熵，∣ S v ∣ / ∣ S ∣ |S_v|/|S| ∣Sv∣/∣S∣ 表示 S S S 中的值数量与数据集 S S S 中值总数之比。

举个例子，假设有如下 "Play Tennis" 数据集：

Day	Outlook	Temp	Humidity	Wind	Tennis
1	Sunny	Hot	High	Weak	No
2	Sunny	Hot	High	Strong	No
3	Overcast	Hot	High	Weak	Yes
4	Rain	Mild	High	Weak	Yes
5	Rain	Cool	Normal	Weak	Yes
6	Rain	Cool	Normal	Strong	No
7	Overcast	Cool	Normal	Weak	Yes
8	Sunny	Mild	High	Weak	No
9	Sunny	Cool	Normal	Weak	Yes
10	Rain	Mild	Normal	Weak	Yes
11	Sunny	Mild	Normal	Strong	Yes
12	Overcast	Mild	High	Strong	Yes
13	Overcast	Hot	Normal	Weak	Yes
14	Rain	Mild	High	Strong	No

先计算 数据集的整体熵，可以通过计算 Play Tennis 为 Yes 的天数比例（ 9 / 14 9/14 9/14）以及 Play Tennis 为 No 的天数比例（ 5 / 14 5/14 5/14）来得到，将这些数值代入上面的熵公式，

Entropy ( Tennis ) = − ( 9 / 14 ) log ⁡ 2 ( 9 / 14 ) -- ( 5 / 14 ) log ⁡ 2 ( 5 / 14 ) = 0.94 \text{Entropy} (\text{Tennis}) = -(9/14) \log_2(9/14) -- (5/14) \log_2 (5/14) = 0.94 Entropy(Tennis)=−(9/14)log2(9/14)--(5/14)log2(5/14)=0.94

随后可以 分别计算每个属性的信息增益 。注意先 计算该属性的子集熵，例如属性 Humidity，

当 Humidity = High：
Entropy ( High ) = − 3 7 log ⁡ 2 3 7 − 4 7 log ⁡ 2 4 7 ≈ 0.985 \text{Entropy}(\text{High}) = -\frac{3}{7}\log_2\frac{3}{7} - \frac{4}{7}\log_2\frac{4}{7} \approx 0.985 Entropy(High)=−73log273−74log274≈0.985

当 Humidity = Normal：
Entropy ( Normal ) = − 6 7 log ⁡ 2 6 7 − 1 7 log ⁡ 2 1 7 ≈ 0.592 \text{Entropy}(\text{Normal}) = -\frac{6}{7}\log_2\frac{6}{7} - \frac{1}{7}\log_2\frac{1}{7} \approx 0.592 Entropy(Normal)=−76log276−71log271≈0.592

信息增益 = 整体熵 -- 划分后的加权平均熵。属性 Humidity 的信息增益如下：

Gain ( Tennis , Humidity ) = 0.94 − ( 7 / 14 ) ∗ ( 0.985 ) -- ( 7 / 14 ) ∗ ( 0.592 ) = 0.151 \text{Gain} (\text{Tennis}, \text{Humidity}) = 0.94 -(7/14)*(0.985) -- (7/14)*(0.592) = 0.151 Gain(Tennis,Humidity)=0.94−(7/14)∗(0.985)--(7/14)∗(0.592)=0.151

然后，对上表中 每个属性重复计算信息增益 ，并 选择信息增益最高的属性 作为决策树的 第一个划分点。

在本例中，outlook 产生了最高的信息增益 。随后，对每个子树重复该过程。

基尼不纯度

衡量的是：如果按照数据集中的类别分布 随机地为一个样本打标签 ，错误分类的概率 是多少。类似于熵，如果 集合 S S S 是纯的 （即全部属于同一类别），则其 不纯度为零。这可以用以下公式表示：

Gini Impurity ( S ) = 1 − ∑ i ( p i ) 2 \text{Gini}\ \text{Impurity}(S) = 1 - \sum_i (p_i)^2 Gini Impurity(S)=1−i∑(pi)2

S S S 是当前数据集， k k k 是类别数， p i p_i pi 是类别 i i i 在数据集中的比例。

当数据集是纯的（例如全是同一类别），假设 p = 1 p=1 p=1，则 Gini = 1 − 1 2 = 0 \text{Gini} = 1 - 1^2 = 0 Gini=1−12=0，表示完全没有不确定性。
当数据集类别分布越均匀，Gini 值越大，说明不纯度更高。二分类最极端情况： p 1 = 0.5 , p 2 = 0.5 p_1 = 0.5, p_2 = 0.5 p1=0.5,p2=0.5，则 Gini = 1 − ( 0. 5 2 + 0. 5 2 ) = 0.5 \text{Gini} = 1 - (0.5^2 + 0.5^2) = 0.5 Gini=1−(0.52+0.52)=0.5，这就是二分类情况下 Gini 的最大值。

和熵比较，二者趋势类似（纯度越高值越低），但：

熵的数学形式更偏信息论；
Gini 计算更简单，数值范围在二分类时为 ( [ 0 , 0.5 ] [0,0.5] [0,0.5])。
在实际应用（如 CART 决策树）中，常用 Gini 作为默认的划分标准。

决策树中的剪枝

剪枝是 防止决策树过拟合 的重要技术。过拟合发生在 树的深度过大、开始记忆训练数据而不是学习一般模式 时。这会导致在新、未见过的数据上表现不佳。

该技术通过 去除预测能力较弱的分支，降低树的复杂度。它通过帮助树更好地对新数据进行泛化，提升模型性能。它还使模型更简洁且部署更快捷。当决策树过于深且开始捕获数据中的噪声时，这很有用。

决策树的优势

易于理解 ：决策树是 可视化 的，这使得 跟踪决策过程 变得容易。
通用性：可用于分类和回归问题。
无需特征缩放 ：与许多机器学习模型不同，它 不需要我们对数据进行缩放或归一化。
处理非线性关系 ：它能 有效捕捉特征与结果之间的复杂非线性关系。
可解释性：树结构易于解释，帮助用户了解每个决策背后的原因。
处理缺失数据 ：它可以通过使用诸如 分配最常见值 或 在划分时忽略缺失数据 等策略来处理缺失值。

决策树的缺点

过拟合 ：如果 模型太深 ，它们可能会对训练数据过拟合，这意味着它们 记住数据而不是学习一般模式。这会导致在未见过的数据上表现不佳。
不稳定性 ：它可能不稳定，这意味着 数据的微小变化可能导致树结构和预测出现显著差异。
倾向于类别多的特征的偏差 ：它可能会对具有众多不同取值的特征产生偏倚，过度关注这些特征，导致可能遗漏其他重要特征，从而降低预测准确性。
捕捉复杂交互的困难 ：决策树可能 难以捕捉特征之间的复杂交互，这使得它们在某些类型的数据上效果较差。
对于大型数据集计算成本高 ：对于大型数据集，构建和剪枝决策树可能计算量大，尤其是随着树深度增加时。