双向链表的稳定排序
手撕一个双向链表的稳定排序算法。此外禁止在代码中创建新的临时节点。
已知链表节点的定义和测试代码如下:
C++
// ListNode类已经事先实现,不需要考生自行编写其中的代码
class ListNode {
private:
int val_;
ListNode* prev_;
ListNode* next_;
ListNode(int val = 0) : val_(val), prev_(nullptr), next_(nullptr) {} // 特殊限制:禁止考生在代码中创建新的链表节点
public:
ListNode* get_next() const { return next_; }
ListNode* get_prev() const { return prev_; }
int get_data() const { return val_; }
void set_next(ListNode* next) { next_ = next; }
void set_prev(ListNode* prev) { prev_ = prev; }
// 构建链表,禁止考生在sort函数中调用
static ListNode* BuildList(const std::vector<int>& values) {
ListNode dummy;
ListNode* list_tail = &dummy;
for (int val : values) {
ListNode* node = new ListNode(val);
if (list_tail != &dummy) {
node->set_prev(list_tail);
}
list_tail->set_next(node);
list_tail = node;
}
return dummy.next_;
}
};
// 测试代码
int main() {
ListNode* list = ListNode::BuildList({2, 1, 6, 0, 9, 1, 9, 8, 4, 4});
list = sort(list);
ListNode* last = nullptr;
while (list) {
std::cout << list->get_data() << " ";
last = list;
list = list->get_next();
}
std::cout << std::endl;
while (last) {
std::cout << last->get_data() << " ";
last = last->get_prev();
}
}插入排序解法
C++
ListNode* sort(ListNode* list_head) {
if (!list_head) {
return nullptr;
}
ListNode* curr = list_head->get_next();
// 将list_head与后续链表断开
if (curr) {
curr->set_prev(nullptr);
}
// list_head在逻辑上作为新链表的
list_head->set_next(nullptr);
list_head->set_prev(nullptr);
// 不停地把curr给摘到以list_head为头节点的链表当中去
while (curr != nullptr) {
ListNode* next_curr = curr->get_next();
ListNode* last_new_list_node = nullptr;
ListNode* new_list_node = list_head;
// 为了确保排序算法的稳定性,这里使用<=而不是<
while (new_list_node && new_list_node->get_data() <= curr->get_data()) {
last_new_list_node = new_list_node;
new_list_node = new_list_node->get_next();
}
// 考虑三种情况:
// 1. 最常规的情况,插入在某个已存在的节点之前
// 2. 插入在链表头节点之前
// 3. 插入在链表尾节点之后
// new_list_node->get_data() > curr->get->data(),将curr插入在new_list_node之前
if (new_list_node) {
curr->set_next(new_list_node);
curr->set_prev(new_list_node->get_prev());
if (new_list_node->get_prev()) {
new_list_node->get_prev()->set_next(curr);
}
new_list_node->set_prev(curr);
// 如果curr被插入到了新链表的头部,需要更新list_head指针
if (curr->get_prev() == nullptr) {
list_head = curr;
}
} else {
last_new_list_node->set_next(curr);
curr->set_next(nullptr);
curr->set_prev(last_new_list_node);
}
curr = next_curr;
}
return list_head;
}归并排序解法
C++
ListNode* sort(ListNode* list_head) {
if (!list_head) {
return nullptr;
}
if (!list_head->get_next()) {
return list_head;
}
// 找到链表的中点,将链表一分为二
ListNode* slow = list_head;
ListNode* fast = list_head->get_next();
while (fast && fast->get_next()) {
slow = slow->get_next();
fast = fast->get_next()->get_next();
}
ListNode* right_list_head = slow->get_next();
if (right_list_head) {
right_list_head->set_prev(nullptr);
}
slow->set_next(nullptr);
// 对两部分链表分别进行排序
ListNode* left = sort(list_head);
ListNode* right = sort(right_list_head);
// 将排序好的链表进行归并
ListNode* new_list_head = nullptr;
ListNode* new_list_tail;
// 初始化头节点
// 1. left和right均不为空,取最小者
// 2. left不为空
// 3. right不为空
if (left && right) {
if (left->get_data() <= right->get_data()) {
new_list_head = left;
left = left->get_next();
} else {
new_list_head = right;
right = right->get_next();
}
} else if (left) {
new_list_head = left;
left = left->get_next();
} else {
new_list_head = right;
right = right->get_next();
}
new_list_tail = new_list_head;
new_list_head->set_next(nullptr);
new_list_head->set_prev(nullptr);
while (left && right) {
if (left->get_data() <= right->get_data()) {
new_list_tail->set_next(left);
left->set_prev(new_list_tail);
new_list_tail = left;
left = left->get_next();
} else {
new_list_tail->set_next(right);
right->set_prev(new_list_tail);
new_list_tail = right;
right = right->get_next();
}
}
while (left) {
new_list_tail->set_next(left);
left->set_prev(new_list_tail);
new_list_tail = left;
left = left->get_next();
}
while (right) {
new_list_tail->set_next(right);
right->set_prev(new_list_tail);
new_list_tail = right;
right = right->get_next();
}
// 返回归并好的链表
return new_list_head;
}求N阶格雷码
下图展示了1~3阶格雷码的变化规律。
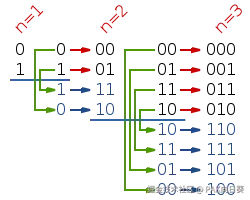
从图中我们可以知道,要计算3阶格雷码,可以先对2阶格雷码作镜像翻转,然后分别在编码的最前面补0或1。
现在请你编写一个程序,输入一个整数N和i(i≥0),打印N阶格雷码中的第i个具体的格雷码。
输入用例1:
3 3输出用例1:
010输入用例1:
4 6输出用例1:
yaml
0101暴力解法
直接上模拟,可以过90%的测试用例。
时间复杂度和空间复杂度均为O(2^N)
C++
#include <iostream>
#include <vector>
#include <list>
int main() {
std::ios_base::sync_with_stdio(true);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int level, index;
std::cin >> level >> index;
std::vector<std::list<uint8_t>> ar = {{0},{1}};
for (int i = 0; i < level - 1; ++i) {
// 添加翻转项
for (int a = ar.size() - 1; 0 <= a; --a) {
ar.push_back(ar[a]);
}
// 头插0、1
for (int a = 0; a < ar.size() / 2; ++a) {
ar[a].push_front(0);
}
for (int a = ar.size() / 2; a < ar.size(); ++a) {
ar[a].push_front(1);
}
}
// 输出答案
for (int bit : ar[index]) {
std::cout << bit;
}
}递归解法
暴力解法中我们需要枚举出所有的N阶格雷码,这意味着其中有至少2*N-1这个量级的空间是浪费的。(实在太夸张了!)
那既然我们已经知道要求N阶格雷码当中具体第几个格雷码了,能不能把这些无谓的计算和空间都给省略掉呢?
答案是肯定的。注意到要求解"求N阶格雷码中的第i个编码"这个原问题,可以先求解"求N-1阶格雷码中的第i'个编码"(i'可以通过i推导出来)这个子问题,然后给子问题的答案加上前缀"0"或"1"即可。
代码写出来是非常简单而优雅的。且时间和空间复杂度均为O(N),远远优于暴力模拟:
C++
#include <iostream>
#include <string>
#include <cmath>
#include <algorithm>
std::string Solve(int n, int i) {
if (n == 0) {
return "";
}
int half = 1 << (n - 1);
if (i < half) {
return "0" + Solve(n - 1, i);
} else {
return "1" + Solve(n - 1, 2 * half - i - 1);
}
}
int main() {
std::ios_base::sync_with_stdio(false);
std::cin.tie(nullptr);
int n, i;
std::cin >> n >> i;
std::cout << Solve(n, i);
return 0;
}递推解法
很显然刚才的递归算法是一个尾递归,我们可以直接将它展开为正向求解的递推算法,从而将空间复杂度降低到O(1)。
C++
#include <iostream>
#include <string>
#include <cmath>
#include <algorithm>
int main() {
std::ios_base::sync_with_stdio(false);
std::cin.tie(nullptr);
int n, i;
std::cin >> n >> i;
std::string ans;
for (; 0 < n; --n) {
int half = 1 << (n - 1);
if (i < half) {
ans.push_back('0');
}
else {
ans.push_back('1');
i = 2 * half - i - 1;
}
}
std::cout << ans;
return 0;
}正则表达式匹配
给定一个待检测字符串s和一个正则表达式p,请你编写一个程序来检测s是否完全匹配p。
已知s仅有小写英文字母构成,p中除了小写英文字母外,还包括以下几种特殊字符:
- ".":匹配任何的单个字符
- "*":匹配零个或多个正则表达式当中它前面的那一个字符
- "?":匹配一个或多个正则表达式当中它前面的那一个字符 题目保证输入的p一定是合法的正则表达式。
需特别强调,所谓完全匹配,是要求p能够描述整个完整的字符串s,而不是s当中的某个子串。
输入输出
输入的第一行为测试用例的总数t。接下来的t行,每一行都有一个s和p。
对于这t行输入,如果p可以匹配s,那么输出true,否则输出false。
测试用例
输入:
css
3
aa a
aa aa
aaa aa输出:
arduino
false
true
false输入:
css
5
a a.
a a.*
ab .*
ab .?
b a?输出:
arduino
false
true
true
true
false递归解法
暴力递归的时间复杂度大约在O(2^(m+n))这个数量级。如果给算法再引入一个记忆化数组来缓存子问题的答案,时间复杂度可以下降到O(m*n)。
以下是没有加优化的暴力递归实现:
C++
#include <iostream>
#include <string>
bool IsMatchImpl(const std::string& s, const std::string& p, int i, int j) {
if (j == p.size()) {
return i == s.size();
}
bool has_quantifier = j + 1 < p.size() && (p[j + 1] == '*' || p[j + 1] == '?');
if (!has_quantifier) {
if (i < s.size() && (s[i] == p[j] || p[j] == '.')) {
return IsMatchImpl(s, p, i + 1, j + 1);
}
else {
return false;
}
}
else if (p[j + 1] == '*') {
return IsMatchImpl(s, p, i, j + 2) || // 匹配0个
i < s.size() && (s[i] == p[j] || p[j] == '.') && IsMatchImpl(s, p, i + 1, j); // 匹配1个及以上
}
else if (p[j + 1] == '?') {
if (i < s.size() && (s[i] == p[j] || p[j] == '.')) {
return IsMatchImpl(s, p, i + 1, j + 2) || // 仅匹配1个
IsMatchImpl(s, p, i + 1, j); // 匹配1个以上
}
else {
return false;
}
}
return false;
}
int main() {
int t;
std::cin >> t;
while (t--) {
std::string s;
std::string p;
std::cin >> s >> p;
if (IsMatchImpl(s, p, 0, 0)) {
std::cout << "true" << std::endl;
} else {
std::cout << "false" << std::endl;
}
}
}动态规划解法
我们可以将上面自顶向下的递归函数进行展开,得到自底向上的动态规划解法。
时间复杂度和空间复杂度均为O(m*n)。
C++
#include <iostream>
#include <string>
#include <vector>
/*
".":匹配任何的单个字符
"*":匹配零个或多个正则表达式当中它前面的那一个字符
"?":匹配一个或多个正则表达式当中它前面的那一个字符
题目保证输入的p一定是合法的正则表达式。
*/
bool IsMatchImpl(const std::string& s, const std::string& p) {
int s_len = s.size();
int p_len = p.size();
std::vector<std::vector<bool>> dp(s_len + 1,
std::vector<bool>(p_len + 1, false));
dp[0][0] = true;
for (int j = 1; j <= p_len; ++j) {
if (p[j - 1] == '*') {
dp[0][j] = dp[0][j - 2];
}
}
for (int i = 1; i <= s_len; ++i) {
for (int j = 1; j <= p_len; ++j) {
if (p[j - 1] == '*') {
// 匹配0个
dp[i][j] = dp[i][j - 2];
// 匹配1个
if (s[i - 1] == p[j - 2] || p[j - 2] == '.') {
dp[i][j] = dp[i][j] || dp[i - 1][j];
}
}
else if (p[j - 1] == '?') {
if (s[i - 1] == p[j - 2] || p[j - 2] == '.') {
// 之前已经匹配过至少1个了 || 当前是匹配的第一个
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - 2];
}
}
else if (s[i - 1] == p[j - 1] || p[j - 1] == '.') {
dp[i][j] = dp[i - 1][j - 1];
}
}
}
return dp.back().back();
}
int main() {
int t;
std::cin >> t;
while (t--) {
std::string s;
std::string p;
std::cin >> s >> p;
std::cout << (IsMatchImpl(s, p) ? "true" : "false") << std::endl;
}
}树苗生长
有一块9*9的正方形棋盘,规定横向为x轴,纵向为y轴,并且左上角格子为坐标原点(0, 0)。那么棋盘中每个格子的位置都可以用(x,y)(0≤x,y≤8)来表示。
现在小明在棋盘上按顺序种植任意数量的树苗(会占用一个格子)。每棵小树苗在种植后会沿已知的一个方向生长繁衍,直到达到最大生长高度、遇到障碍。
请你编写一个程序,用于判断在种植完所有树苗、并且所有树苗均结束生长后,当前棋盘上是否存在由树苗围成的矩形封闭结构?
名词解释:
- 最大生长高度(max_grow_len):树苗向特定方向可以繁衍生长的最大格子数量(不包含它一开始被种植的位置)。例如,初始位置为(8, 0)、最大生长高度为为7、生长方向为向下的树苗在生长完毕后,会占用(8,0)~(8,7)这8个格子。
- 生长方向:上、右、下、左,依次用整数表示0、1、2、3表示。
- 障碍:当某棵树苗在生长方向上繁衍时,遇到已经存在的树苗,或者已经抵达棋盘边界,则立即停止生长(即使在该方向上还没有达到最大生长高度)。
- 种植顺序:当且仅当上一棵种植的树苗结束生长繁衍后,小明才会种植下一棵树苗。也就是说,棋盘上不可能同时出现两棵树苗正在生长繁衍的情况。另外,如果小明发现种植某颗树苗时,该位置已经被已有树苗占用,则会直接放弃种植当前树苗,直接开始尝试种植下一棵树苗。
输入输出
输入N行数据,代表依次种植的N棵树苗。
第i行输入由四个非负整数x, y, d, m构成,分别表示第i棵树苗的种植位置(x, y)、树苗的生长方向d、最大生长高度m。
输出字符串"true"或"false",表示种植和树苗生长全部结束后,当前棋盘上是否存在矩形封闭结构。
测试用例
测试用例1
输入:
0 0 1 7
8 0 2 7
8 8 3 7
0 8 0 7输入:
arduino
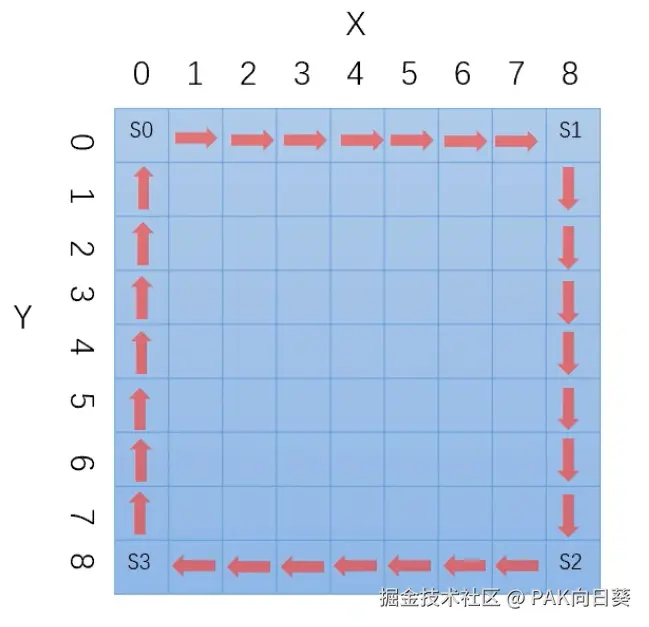
true说明:
输入含有4行,说明小明会依次种植4棵树苗:
- 第1棵树苗的种植坐标为(0, 0),向右生长,最大生长高度为7。
- 第2棵树苗的种植坐标为(8, 0),向下生长,最大生长高度为7。
- 第3棵树苗的种植坐标为(8, 8),向左生长,最大生长高度为7。
- 第4棵树苗的种植坐标为(0, 8),向上生长,最大生长高度为7。
最终棋盘的情况如下图所示,可见其中存在一个被树苗围成的矩形,因此我们的程序会打印"true"。
测试用例2
输入:
0 0 1 7
8 0 2 7
8 8 3 7
0 8 0 6输入:
arduino
false模拟+暴力检测
考虑到棋盘的大小是固定的,因此我们可以直接先模拟所有树苗的种植和生长情况,得到所有树苗种植完毕并完成生长的棋盘。
然后暴力枚举所有潜在的矩形左上角顶点和右下角顶点,看看它们围成的区域是否是合法的矩形。暴力检测的时间复杂度大约在O(9*9*9*9*9)这个数量级,还是很可以接受的。
C++
#include <iostream>
#include <vector>
#define N (9)
#define IN_RANGE(x, l, r) ((l) <= (x) && (x) < (r))
int board[N][N] = {0};
// 上,右,下,左
int grow_dir_di[] = {-1, 0, 1, 0};
int grow_dir_dj[] = {0, 1, 0, -1};
void PlacePlantAndGrow(int start_i, int start_j, int grow_dir, int max_grow_len) {
int cur_i = start_i;
int cur_j = start_j;
int cur_grow_len = 0;
while (IN_RANGE(cur_i, 0, N) && IN_RANGE(cur_j, 0, N) && cur_grow_len <= max_grow_len && !board[cur_i][cur_j]) {
board[cur_i][cur_j] = 1;
cur_i += grow_dir_di[grow_dir];
cur_j += grow_dir_dj[grow_dir];
++cur_grow_len;
}
}
bool HasValidRectangle() {
// 暴力枚举左上角点
for (int left_top_i = 0; left_top_i < N; ++left_top_i) {
for (int left_top_j = 0; left_top_j < N; ++left_top_j) {
// 如果左上角点没有树苗,直接放弃枚举右下角点
if (!board[left_top_i][left_top_j]) continue;
// 暴力枚举右下角点
for (int right_bottom_i = left_top_i + 2; right_bottom_i < N; ++right_bottom_i) {
for (int right_bottom_j = left_top_j + 2; right_bottom_j < N; ++right_bottom_j) {
bool is_valid_rect = true;
// 检测矩形竖向的两条边是否是封闭的
for (int test_i = left_top_i; test_i <= right_bottom_i; ++test_i) {
if (!board[test_i][left_top_j] || !board[test_i][right_bottom_j]) {
is_valid_rect = false;
break;
}
}
if (!is_valid_rect) continue;
// 检测矩形横向的两条边是否是封闭的
for (int test_j = left_top_j; test_j <= right_bottom_j; ++test_j) {
if (!board[left_top_i][test_j] || !board[right_bottom_i][test_j]) {
is_valid_rect = false;
break;
}
}
if (is_valid_rect) {
return true;
}
}
}
}
}
return false;
}
int main() {
int j, i, grow_dir, max_grow_len;
while (std::cin >> j >> i >> grow_dir >> max_grow_len) {
PlacePlantAndGrow(i, j, grow_dir, max_grow_len);
}
std::cout << (HasValidRectangle() ? "true" : "false") << std::endl;
}