旋转图像 - 技术栈

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

旋转规律（以3阶矩阵为例）： (0,0) -> (0,2) (0,1) -> (1,2) (0,2) -> (2,2) (1,0) -> (0,1) (1,1) -> (1,1) (1,2) -> (2,1) (2,0) -> (0,0) (2,1) -> (1,2) (2,2) -> (2,0)

总结规律：matrix[j][n-1-i]=matrix[i][j] 。

方法一：通过翻转代替旋转

旋转公式可通过一次水平翻转+一次转置实现，水平翻转：matrix[n-1-i][j]=matrix[i][j] ;转置：matrix[j][n-1-i]=matrix[n-1-i][j]。

所以只需根据上述思想编写两次变换的代码。

python 复制代码

class Solution(object):
    def rotate(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: None Do not return anything, modify matrix in-place instead.
        """
        n = len(matrix)
        
        #水平对称，互换进行n//2次
        for i in range(n//2):
            for j in range(n):
                tmp = matrix[i][j]
                #对应对称公式
                matrix[i][j] = matrix[n-i-1][j]
                matrix[n-i-1][j] = tmp
        #转置
        for i in range(n):
            for j in range(i):
                tmp = matrix[i][j]
                #转置公式
                matrix[i][j] = matrix[j][i]
                matrix[j][i] = tmp

方法二：原地旋转

直接使用旋转公式将所有值进行旋转，需要同等大小的辅助数组，这会有O(N²)的空间复杂度。怎么才能实现使用一个变量tmp实现原地旋转呢？

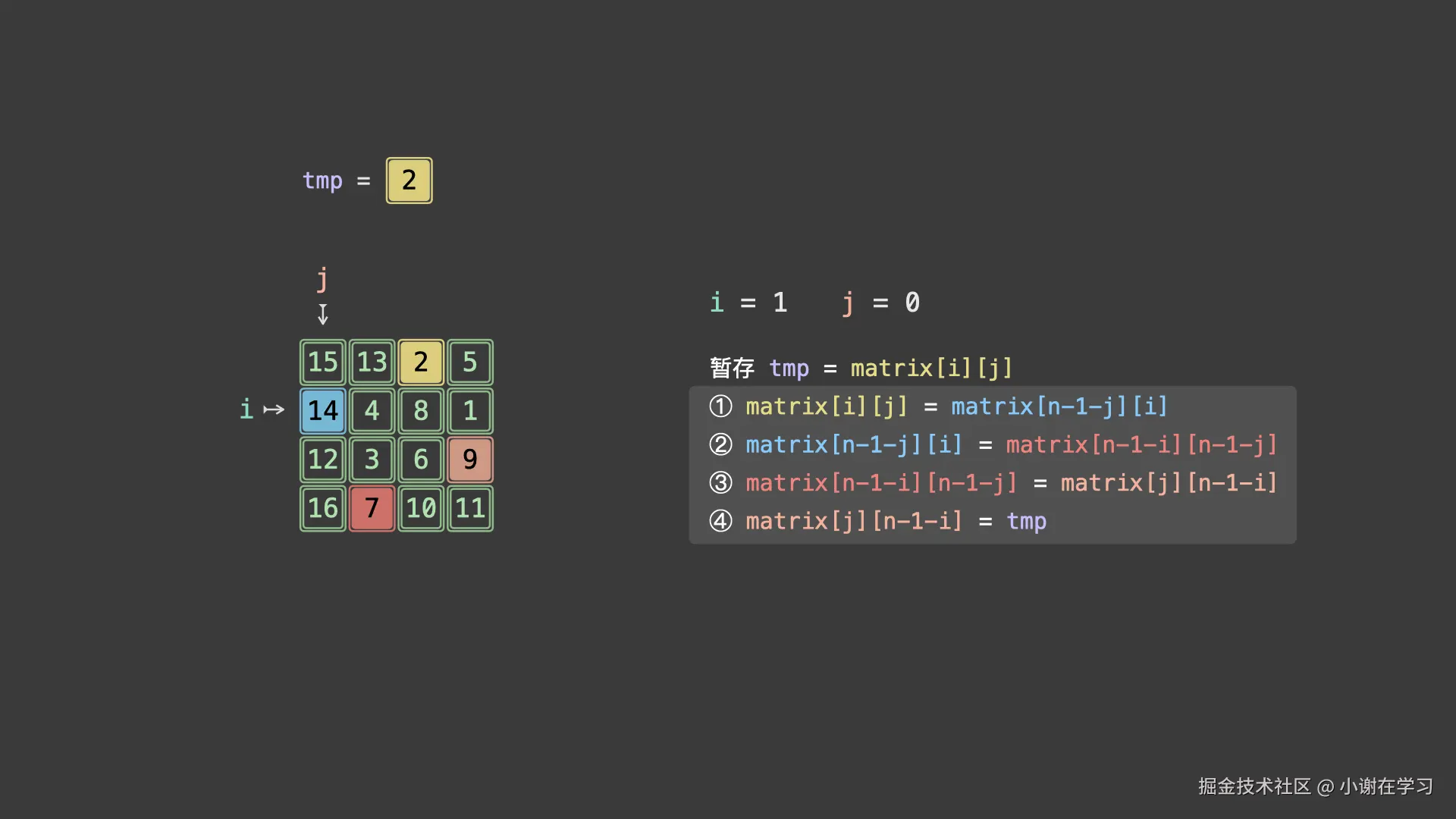
通过观察发现，旋转一周（也就是换四次位置）会有一个数放回最初的位置，相当于是对4个元素进行交换，也就是使用四次旋转公式：

第一个元素改变位置：matrix[j][n-1-i] = matrix[i][j]
第二个元素改变位置：matrix[n-1-i][n-1-j] = matrix[j][n-1-i]
第三个元素改变位置：matrix[n-1-j][i] = matrix[n-1-i][n-1-j]
第四个元素改变位置：matrix[i][j] = matrix[n-1-j][i] 可以由下往上，令tmp = matrix[i][j]，然后一个个将新值赋值给上一个位置，最后matrix[j][n-1-i] = tmp。

看总共需要循环多少次：

每次循环改变四个元素的位置，外层循环改变行，内层循环改变列；
由于这改变的四个元素，存在前半部分的行换到后半部分和前半部分的列换到后半部分；
所以对于外层循环，即行，需进行N//2次
对于列，需要进行(N+1)//2次，保证单数列位置的列能够旋转。

^图片来源：leetcode.cn/problems/ro...^

问题：为什么遍历行的时候不是进行(N+1)//2次？

因为对最后一行变换时只有一个元素，不需要修改。

python 复制代码

class Solution(object):
    def rotate(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: None Do not return anything, modify matrix in-place instead.
        """
        for i in range(n//2):
            for j in range((n+1)//2):
                tmp = matrix[i][j]
                matrix[i][j] = matrix[n-1-j][i]
                matrix[n-1-j][i] = matrix[n-1-i][n-1-j]
                matrix[n-1-i][n-1-j] = matrix[j][n-i-1]
                matrix[j][n-i-1] = tmp