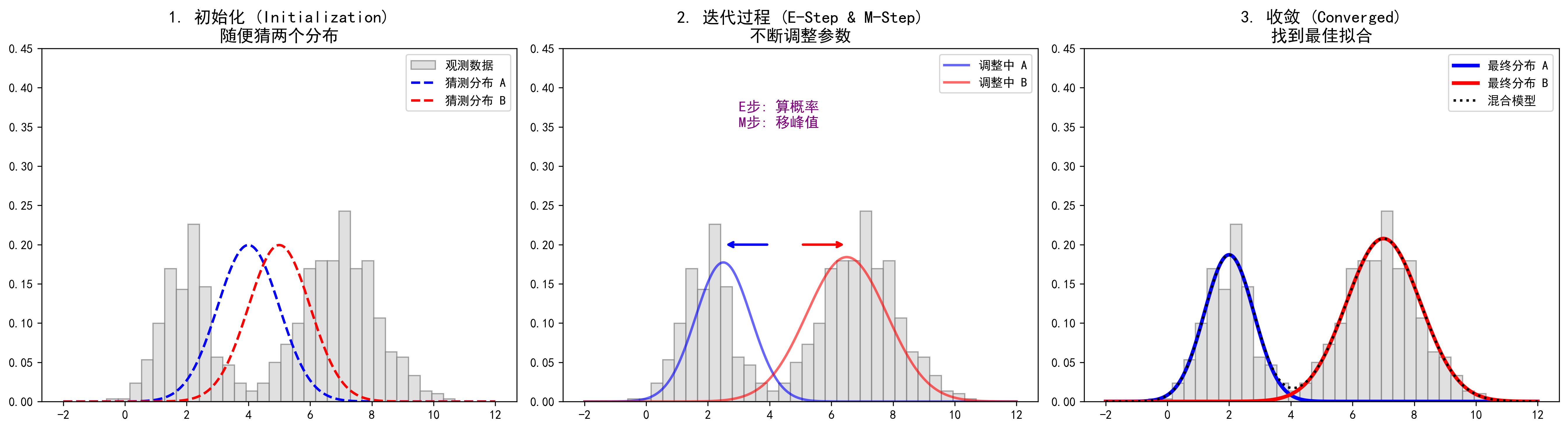
图解说明:
- 📊 灰色直方图:代表我们看到的观测数据(混在一起,分不清谁是谁)。
- 🔵 蓝色虚线/实线:代表我们猜测的分布 A(比如男生身高)。
- 🔴 红色虚线/实线:代表我们猜测的分布 B(比如女生身高)。
- 🟣 中间过程:一开始猜得很离谱(图1),通过不断调整(图2),最后完美拟合了数据(图3)。
今天我们要挑战一个稍微有点"烧脑"但非常有用的算法------EM 算法 (Expectation-Maximization) ,中文叫期望最大化算法。
别被名字吓跑了!它的核心逻辑其实非常像我们生活中的**"猜谜游戏"**。
如果你完全不懂算法,没关系。想象一下,你是一个侦探。
1. 它是解决什么问题的?(举个栗子)
假设你手里有一张纸条,上面写着 100 个人的身高数据 (比如 175, 162, 180, 158...)。
你知道这群人里既有男生 ,也有女生 。
一般来说,男生的平均身高要高一些,女生的平均身高要矮一些。
但是,这张纸条上没有标注性别!你只看到一堆数字,完全不知道哪个是男,哪个是女。
你的任务是:根据这堆混乱的数字,推算出男生和女生的平均身高分别是多少。
遇到的死结
这就陷入了一个**"鸡生蛋,蛋生鸡"**的死循环:
- 要想算出男生的平均身高 ,我得先知道哪些数据是男生的。
- 要想知道哪些数据是男生的 ,我得先知道男生的平均身高(比如这个数是 180,离男生平均值近,我才敢说他是男的)。
两个都不知道,怎么办?
EM 算法说:"别管那么多,先瞎猜一个,然后慢慢调整!"
2. EM 算法的"两步走"策略
EM 算法就像是一个不断反悔的侦探,它通过两个步骤循环操作,直到找到真相。
第一步:E 步 (Expectation) ------ 先瞎猜,算期望
既然不知道男生女生的平均身高,那我就先随便假设一个!
- 假设:男生平均 170cm,女生平均 160cm。
有了这个假设,我就可以去推测每一个身高数据属于谁了。
- 数据 180cm :离男生平均值 (170) 更近,离女生 (160) 远。那它大概率是男生(比如 90% 可能是男,10% 可能是女)。
- 数据 165cm :这就不好说了,卡在中间,可能一半一半吧。
没错,我们要对这 100 个数据,每一个都这样算一遍概率!
这时候,我们不再是"非黑即白"地说是男是女,而是给每个数据分配一个**"身份概率"**(权重)。
第二步:M 步 (Maximization) ------ 根据猜测,更新参数
现在,我们假装刚才猜的"身份概率"就是真的。
- 既然 180cm 主要是男生,那在算男生平均身高时,它的发言权就很大。
- 既然 165cm 是一半一半,那它对男女平均身高的贡献就各占一半。
根据这个重新分配好的权重,我们重新计算男生和女生的平均身高。
怎么算呢?用"加权平均":
- 新的男生平均 :把所有人的身高乘上他是男生的概率,再加起来除以总权重。
- 计算公式:
(180×0.9 + 165×0.5 + ...) ÷ (0.9 + 0.5 + ...) - 结果可能变成了 175cm(因为高个子在男生这边的权重更大)。
- 计算公式:
- 新的女生平均 :把所有人的身高乘上她是女生的概率,再加起来除以总权重。
- 计算公式:
(180×0.1 + 165×0.5 + ...) ÷ (0.1 + 0.5 + ...) - 结果可能变成了 158cm。
- 计算公式:
循环往复
有了新的平均值 (175, 158) ,我们再回到 E 步:
- 重新评估每个身高数据是男是女(这时候判断会更准,170cm 以前可能被当成男生,现在离 175 远了,可能被当成女生)。
- 然后再进 M 步,更新平均值。
就这样 E -> M -> E -> M 一直转圈,直到最后参数不再变化为止。
3. 为什么叫"期望最大化"?
- E (Expectation) :计算期望。就是在参数已知的情况下,猜测数据隐含的类别(填补缺失数据)。
- M (Maximization) :最大化似然函数。就是在数据补全的情况下,寻找最能解释这些数据的参数。
简单说就是:猜数据 -> 算参数 -> 再猜数据 -> 再算参数。
4. EM 算法的优缺点
✅ 优点 (为什么它厉害?)
- 解决缺失数据:它最擅长处理这种"含有隐变量"(也就是有一部分信息你看不到)的问题。
- 自动聚类:著名的高斯混合模型 (GMM) 就是用 EM 算法训练的,它可以把数据自动分成几个正态分布的波峰。
❌ 缺点 (也要注意)
- 容易陷入局部最优:如果你一开始瞎猜的参数太离谱,它可能最后收敛到一个错误的结果(走进了死胡同),而不是全局最好的结果。
- 收敛慢:有时候要转很多圈才能停下来。
5. 总结
EM 算法 就是一个**"试错法"大师**:
- 面对一团乱麻(既不知道类别,也不知道参数)。
- 它先随便给个初始值。
- E步:根据参数猜类别(心里有个底)。
- M步:根据类别算参数(修正模型)。
- 反复横跳,直到找到最合理的解释。
就像你在大雾天开车,看不清路(隐变量),你只能先凭感觉开(E步),看到路标后再修正方向(M步),一点点逼近目的地!🌫️