数据可视化 | Violin Plot小提琴图Python实现数据分布密度可视化科研图表

引言

小提琴图（Violin Plot）是一种强大的统计图表类型，它结合了箱线图和核密度估计图的优点，能够同时展示数据的分布形状、统计摘要和概率密度信息。在科研数据可视化中，小提琴图特别适用于比较多组数据的分布特征，是箱线图的理想替代方案。本文将详细介绍如何使用Python实现各种类型的小提琴图，包括基础小提琴图、统计增强型、分组对比等。

小提琴图的核心优势在于：

完整分布信息：不仅显示四分位数，还展示数据的密度分布
多组对比：便于比较不同组别的数据分布差异
异常值检测：结合箱线图显示离群点
科研级质量 ：符合学术期刊的发表标准

理论基础

小提琴图的构成要素

小提琴图由以下几个部分组成：

密度曲线：使用核密度估计（KDE）展示数据分布形状
箱线图元素：中位数、四分位数、异常值
对称设计：左右对称显示分布密度
多组排列：并排显示便于对比

核密度估计

核密度估计是小提琴图的核心算法：

f^(x)=1nh∑i=1nK(x−xih) \hat{f}(x) = \frac{1}{nh} \sum_{i=1}^{n} K\left(\frac{x - x_i}{h}\right) f^(x)=nh1i=1∑nK(hx−xi)

其中：

K 是核函数（通常为高斯核）
h 是带宽参数
n 是样本数量

高斯核函数 ：
K(u)=12πe−u22 K(u) = \frac{1}{\sqrt{2\pi}} e^{-\frac{u^2}{2}} K(u)=2π 1e−2u2

带宽选择

带宽 h 的选择影响密度估计的平滑程度：

带宽过小：过度拟合，显示过多细节
带宽过大：过度平滑，丢失重要特征
最优带宽：通常使用Scott法则或Silverman法则

统计意义

小提琴图提供丰富的统计信息：

集中趋势：中位数、均值位置
离散程度：四分位距、分布宽度
分布形状：对称性、峰值数量
异常值：超出1.5倍四分位距的点

代码实现

环境配置

bash 复制代码

pip install numpy>=1.20.0 matplotlib>=3.5.0 seaborn>=0.11.0 scipy>=1.7.0 pandas>=1.3.0 scikit-learn>=1.0.0

核心小提琴图类实现

python 复制代码

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
小提琴图生成器 - 数据分布密度可视化
"""

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
from scipy.stats import gaussian_kde
from typing import List, Tuple, Optional, Dict, Any
import pandas as pd
import warnings
warnings.filterwarnings('ignore')

class ViolinPlotGenerator:
    """小提琴图生成器"""

    def __init__(self, style='academic', figsize=(12, 8)):
        """
        初始化生成器

        Args:
            style: 图表样式 ('academic', 'presentation', 'web')
            figsize: 图表尺寸
        """
        self.style = style
        self.figsize = figsize
        self._setup_style()

    def _setup_style(self):
        """设置绘图风格"""
        if self.style == 'academic':
            # 学术期刊风格
            plt.style.use('default')
            plt.rcParams['font.family'] = ['DejaVu Sans', 'SimHei']
            plt.rcParams['font.size'] = 12
            plt.rcParams['axes.linewidth'] = 1.5
            plt.rcParams['figure.dpi'] = 300
        elif self.style == 'presentation':
            # 演示文稿风格
            plt.style.use('seaborn-v0_8')
            plt.rcParams['font.size'] = 14
            plt.rcParams['figure.dpi'] = 150
        else:
            # Web风格
            plt.style.use('ggplot')
            plt.rcParams['font.size'] = 11

    def create_violin_plot(self, data_groups: List[np.ndarray],
                          labels: Optional[List[str]] = None,
                          title: str = "小提琴图",
                          filename: Optional[str] = None,
                          show_boxplot: bool = True,
                          show_mean: bool = True,
                          alpha: float = 0.7) -> plt.Figure:
        """
        创建基础小提琴图

        Args:
            data_groups: 数据组列表
            labels: 组标签
            title: 图表标题
            filename: 保存文件名
            show_boxplot: 是否显示箱线图
            show_mean: 是否显示均值点
            alpha: 透明度

        Returns:
            matplotlib Figure对象
        """
        if labels is None:
            labels = [f'Group {i+1}' for i in range(len(data_groups))]

        # 准备数据
        data_dict = {}
        for i, (data, label) in enumerate(zip(data_groups, labels)):
            data_dict[label] = data

        df = pd.DataFrame(data_dict)

        # 创建图表
        fig, ax = plt.subplots(figsize=self.figsize)

        # 绘制小提琴图
        violin_parts = ax.violinplot([df[col].values for col in df.columns],
                                   showmeans=show_mean, showextrema=True)

        # 设置颜色
        colors = self._get_colors(len(data_groups))
        for i, pc in enumerate(violin_parts['bodies']):
            pc.set_facecolor(colors[i])
            pc.set_edgecolor('black')
            pc.set_alpha(alpha)
            pc.set_linewidth(1.5)

        # 设置中位线颜色
        if 'cmedians' in violin_parts:
            violin_parts['cmedians'].set_color('black')
            violin_parts['cmedians'].set_linewidth(2)

        # 设置均值点
        if show_mean and 'cmeans' in violin_parts:
            violin_parts['cmeans'].set_color('red')
            violin_parts['cmeans'].set_marker('D')
            violin_parts['cmeans'].set_markersize(6)

        # 添加箱线图
        if show_boxplot:
            bp = ax.boxplot([df[col].values for col in df.columns],
                          positions=range(1, len(df.columns)+1),
                          widths=0.1, patch_artist=True,
                          medianprops=dict(color='black', linewidth=2),
                          boxprops=dict(facecolor='white', edgecolor='black'),
                          whiskerprops=dict(color='black'),
                          capprops=dict(color='black'))

            # 设置箱体颜色
            for patch in bp['boxes']:
                patch.set_facecolor('white')
                patch.set_edgecolor('black')

        # 设置标签
        ax.set_xticks(range(1, len(labels)+1))
        ax.set_xticklabels(labels, rotation=45, ha='right')
        ax.set_title(title, fontsize=16, fontweight='bold', pad=20)
        ax.set_ylabel('Value', fontsize=14)
        ax.grid(True, alpha=0.3, linestyle='--', axis='y')

        plt.tight_layout()

        if filename:
            plt.savefig(f'output/{filename}', dpi=300, bbox_inches='tight')

        return fig

    def create_statistical_violin_plot(self, data_groups: List[np.ndarray],
                                     labels: Optional[List[str]] = None,
                                     title: str = "统计增强小提琴图",
                                     filename: Optional[str] = None) -> plt.Figure:
        """
        创建带统计信息的增强小提琴图
        """
        if labels is None:
            labels = [f'Group {i+1}' for i in range(len(data_groups))]

        # 计算统计信息
        stats_info = []
        for i, data in enumerate(data_groups):
            mean_val = np.mean(data)
            std_val = np.std(data)
            median_val = np.median(data)
            q25, q75 = np.percentile(data, [25, 75])
            iqr = q75 - q25

            stats_info.append({
                'mean': mean_val,
                'std': std_val,
                'median': median_val,
                'q25': q25,
                'q75': q75,
                'iqr': iqr,
                'n': len(data)
            })

        # 创建图表
        fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))

        # 左侧：小提琴图
        data_dict = {label: data for label, data in zip(labels, data_groups)}
        df = pd.DataFrame(data_dict)

        violin_parts = ax1.violinplot([df[col].values for col in df.columns],
                                    showmeans=True, showextrema=True)

        colors = self._get_colors(len(data_groups))
        for i, pc in enumerate(violin_parts['bodies']):
            pc.set_facecolor(colors[i])
            pc.set_edgecolor('black')
            pc.set_alpha(0.7)

        ax1.set_xticks(range(1, len(labels)+1))
        ax1.set_xticklabels(labels, rotation=45, ha='right')
        ax1.set_title('数据分布', fontsize=14, fontweight='bold')
        ax1.grid(True, alpha=0.3)

        # 右侧：统计信息表
        ax2.axis('off')

        # 创建统计表格
        cell_text = []
        for i, (label, stats) in enumerate(zip(labels, stats_info)):
            cell_text.append([
                label,
                '.1f',
                '.1f',
                '.1f',
                '.1f'
            ])

        table = ax2.table(cellText=cell_text,
                         colLabels=['组别', '均值', '标准差', '中位数', '样本量'],
                         loc='center',
                         cellLoc='center',
                         colColours=['lightgray']*5)

        table.auto_set_font_size(False)
        table.set_fontsize(10)
        table.scale(1.2, 1.5)
        ax2.set_title('统计汇总', fontsize=14, fontweight='bold')

        fig.suptitle(title, fontsize=16, fontweight='bold', y=0.98)
        plt.tight_layout()

        if filename:
            plt.savefig(f'output/{filename}', dpi=300, bbox_inches='tight')

        return fig

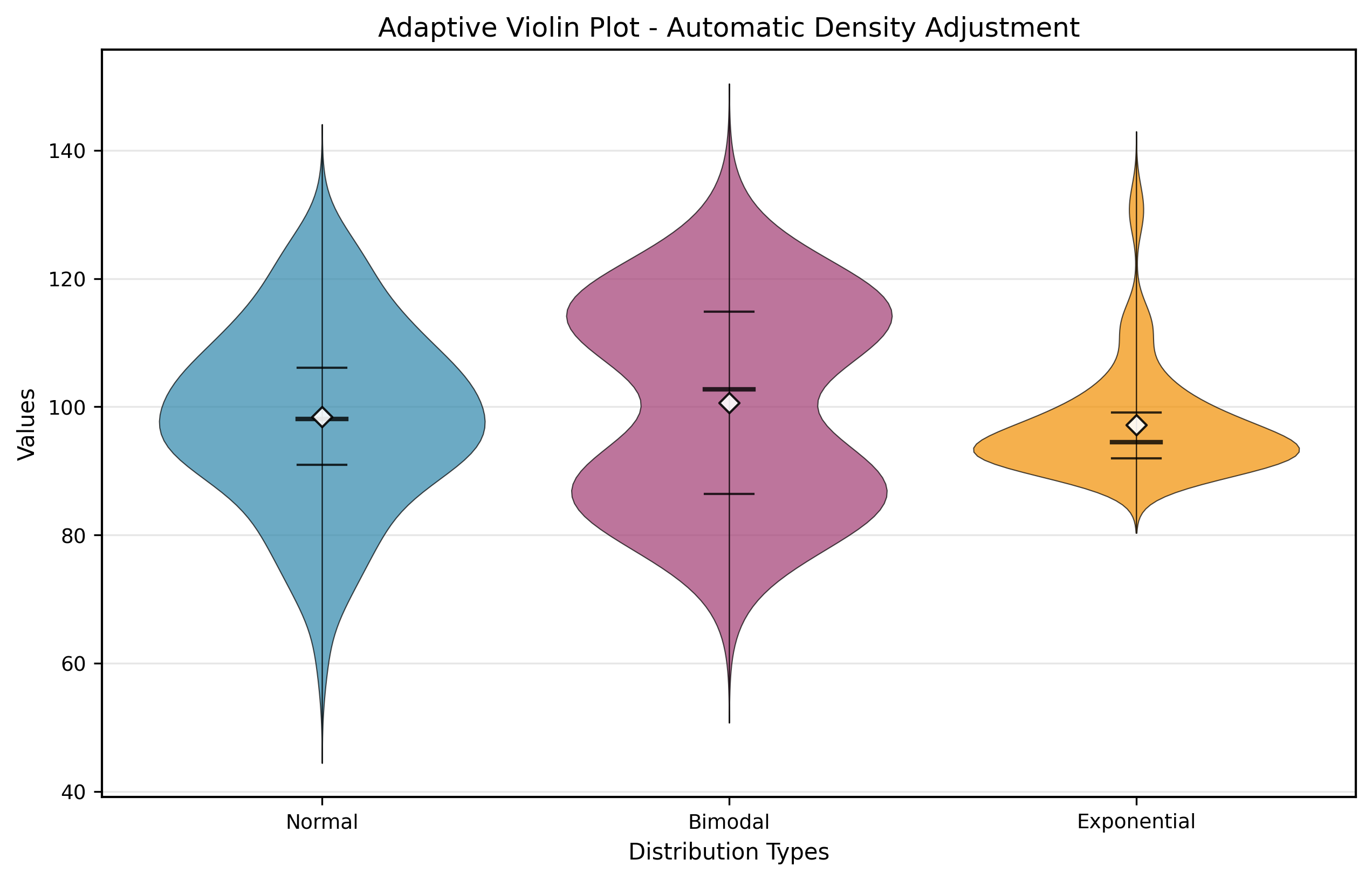
    def create_adaptive_violin_plot(self, data_groups: List[np.ndarray],
                                  labels: Optional[List[str]] = None,
                                  title: str = "自适应小提琴图",
                                  filename: Optional[str] = None) -> plt.Figure:
        """
        创建自适应小提琴图（根据数据特征自动调整）
        """
        if labels is None:
            labels = [f'Group {i+1}' for i in range(len(data_groups))]

        # 分析数据特征
        data_features = []
        for data in data_groups:
            # 计算分布特征
            skewness = stats.skew(data)
            kurtosis = stats.kurtosis(data)

            # 检测分布类型
            if abs(skewness) < 0.5 and abs(kurtosis) < 0.5:
                dist_type = 'normal'
            elif skewness > 1:
                dist_type = 'right_skewed'
            elif skewness < -1:
                dist_type = 'left_skewed'
            elif kurtosis > 1:
                dist_type = 'heavy_tailed'
            else:
                dist_type = 'moderate'

            data_features.append({
                'skewness': skewness,
                'kurtosis': kurtosis,
                'dist_type': dist_type,
                'range': np.ptp(data),
                'cv': np.std(data) / np.mean(data)  # 变异系数
            })

        # 根据特征调整参数
        fig, axes = plt.subplots(2, 2, figsize=(14, 10))
        axes = axes.ravel()

        for i, (data, label, features) in enumerate(zip(data_groups, labels, data_features)):
            ax = axes[i]

            # 根据分布类型调整带宽
            if features['dist_type'] == 'heavy_tailed':
                bw_method = 0.3  # 较小的带宽
            elif features['dist_type'] in ['right_skewed', 'left_skewed']:
                bw_method = 0.5  # 中等带宽
            else:
                bw_method = 'scott'  # 自适应带宽

            # 绘制小提琴图
            violin_parts = ax.violinplot(data, showmeans=True, showextrema=True,
                                       bw_method=bw_method)

            # 设置颜色（根据分布类型）
            color_map = {
                'normal': 'lightblue',
                'right_skewed': 'lightcoral',
                'left_skewed': 'lightgreen',
                'heavy_tailed': 'lightyellow',
                'moderate': 'lightgray'
            }

            for pc in violin_parts['bodies']:
                pc.set_facecolor(color_map[features['dist_type']])
                pc.set_edgecolor('black')
                pc.set_alpha(0.7)

            ax.set_title(f'{label}\n({features["dist_type"]})', fontsize=12)
            ax.grid(True, alpha=0.3)

            # 添加统计信息
            mean_val = np.mean(data)
            std_val = np.std(data)
            ax.text(0.02, 0.98, '.1f',
                   transform=ax.transAxes, fontsize=9, verticalalignment='top',
                   bbox=dict(boxstyle='round', facecolor='white', alpha=0.8))

        fig.suptitle(title, fontsize=16, fontweight='bold', y=0.95)
        plt.tight_layout()

        if filename:
            plt.savefig(f'output/{filename}', dpi=300, bbox_inches='tight')

        return fig

    def _get_colors(self, n_colors: int) -> List[str]:
        """获取颜色列表"""
        if self.style == 'academic':
            base_colors = ['#1f77b4', '#ff7f0e', '#2ca02c', '#d62728', '#9467bd',
                          '#8c564b', '#e377c2', '#7f7f7f', '#bcbd22', '#17becf']
        else:
            base_colors = plt.cm.Set2.colors

        return [base_colors[i % len(base_colors)] for i in range(n_colors)]

    def compare_violin_styles(self, data_groups: List[np.ndarray],
                            labels: Optional[List[str]] = None,
                            filename: Optional[str] = "style_comparison.png"):
        """
        比较不同样式的小提琴图
        """
        if labels is None:
            labels = [f'Group {i+1}' for i in range(len(data_groups))]

        fig, axes = plt.subplots(2, 2, figsize=(16, 12))
        axes = axes.ravel()

        styles = ['基础小提琴图', '带箱线图', '带统计信息', '自适应样式']

        # 样式1：基础小提琴图
        ax = axes[0]
        violin_parts = ax.violinplot(data_groups, showmeans=True)
        for pc in violin_parts['bodies']:
            pc.set_facecolor('lightblue')
            pc.set_alpha(0.7)
        ax.set_title(styles[0], fontsize=14, fontweight='bold')
        ax.set_xticks(range(1, len(labels)+1))
        ax.set_xticklabels(labels, rotation=45, ha='right')

        # 样式2：带箱线图
        ax = axes[1]
        violin_parts = ax.violinplot(data_groups, showmeans=True)
        for pc in violin_parts['bodies']:
            pc.set_facecolor('lightgreen')
            pc.set_alpha(0.7)

        # 添加箱线图
        bp = ax.boxplot(data_groups, positions=range(1, len(data_groups)+1),
                       widths=0.1, patch_artist=True)
        for patch in bp['boxes']:
            patch.set_facecolor('white')

        ax.set_title(styles[1], fontsize=14, fontweight='bold')
        ax.set_xticks(range(1, len(labels)+1))
        ax.set_xticklabels(labels, rotation=45, ha='right')

        # 样式3：使用seaborn
        ax = axes[2]
        data_dict = {label: data for label, data in zip(labels, data_groups)}
        df = pd.DataFrame(data_dict)
        melted_df = df.melt(var_name='Group', value_name='Value')
        sns.violinplot(data=melted_df, x='Group', y='Value', ax=ax, palette='Set2')
        ax.set_title(styles[2], fontsize=14, fontweight='bold')
        ax.tick_params(axis='x', rotation=45)

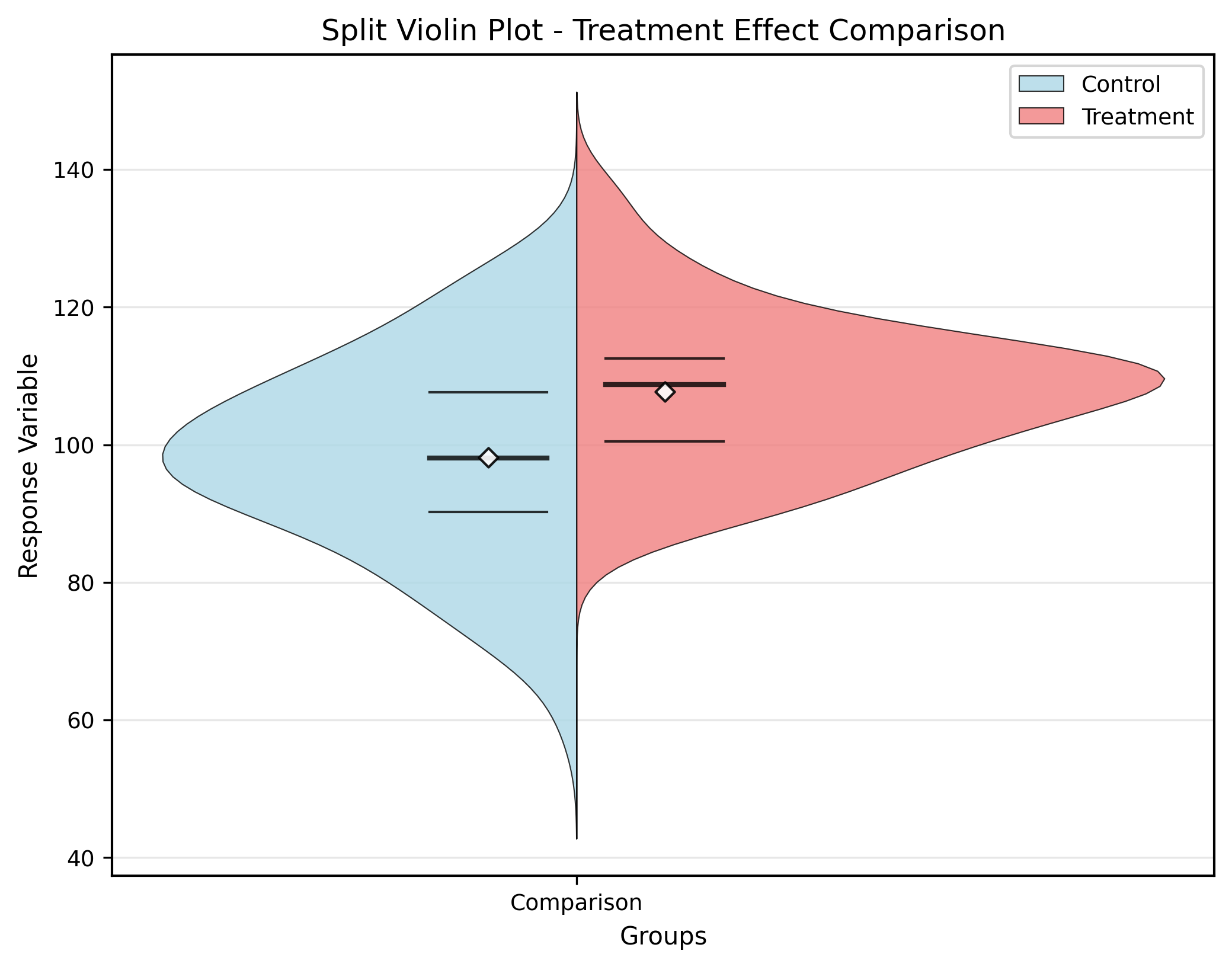
        # 样式4：分割小提琴图
        ax = axes[3]
        # 模拟分割数据（这里使用相同数据作为示例）
        split_data = [data_groups[i] for i in range(len(data_groups)) for _ in range(2)]
        split_labels = [f'{label}\nA' for label in labels] + [f'{label}\nB' for label in labels]

        violin_parts = ax.violinplot(split_data, showmeans=True)
        colors = ['lightcoral', 'lightblue'] * len(labels)
        for i, pc in enumerate(violin_parts['bodies']):
            pc.set_facecolor(colors[i % len(colors)])
            pc.set_alpha(0.7)

        ax.set_title(styles[3], fontsize=14, fontweight='bold')
        ax.set_xticks(range(1, len(split_labels)+1))
        ax.set_xticklabels(split_labels, rotation=45, ha='right')

        fig.suptitle('小提琴图样式对比', fontsize=16, fontweight='bold', y=0.95)
        plt.tight_layout()

        if filename:
            plt.savefig(f'output/{filename}', dpi=300, bbox_inches='tight')

        return fig

可视化效果展示

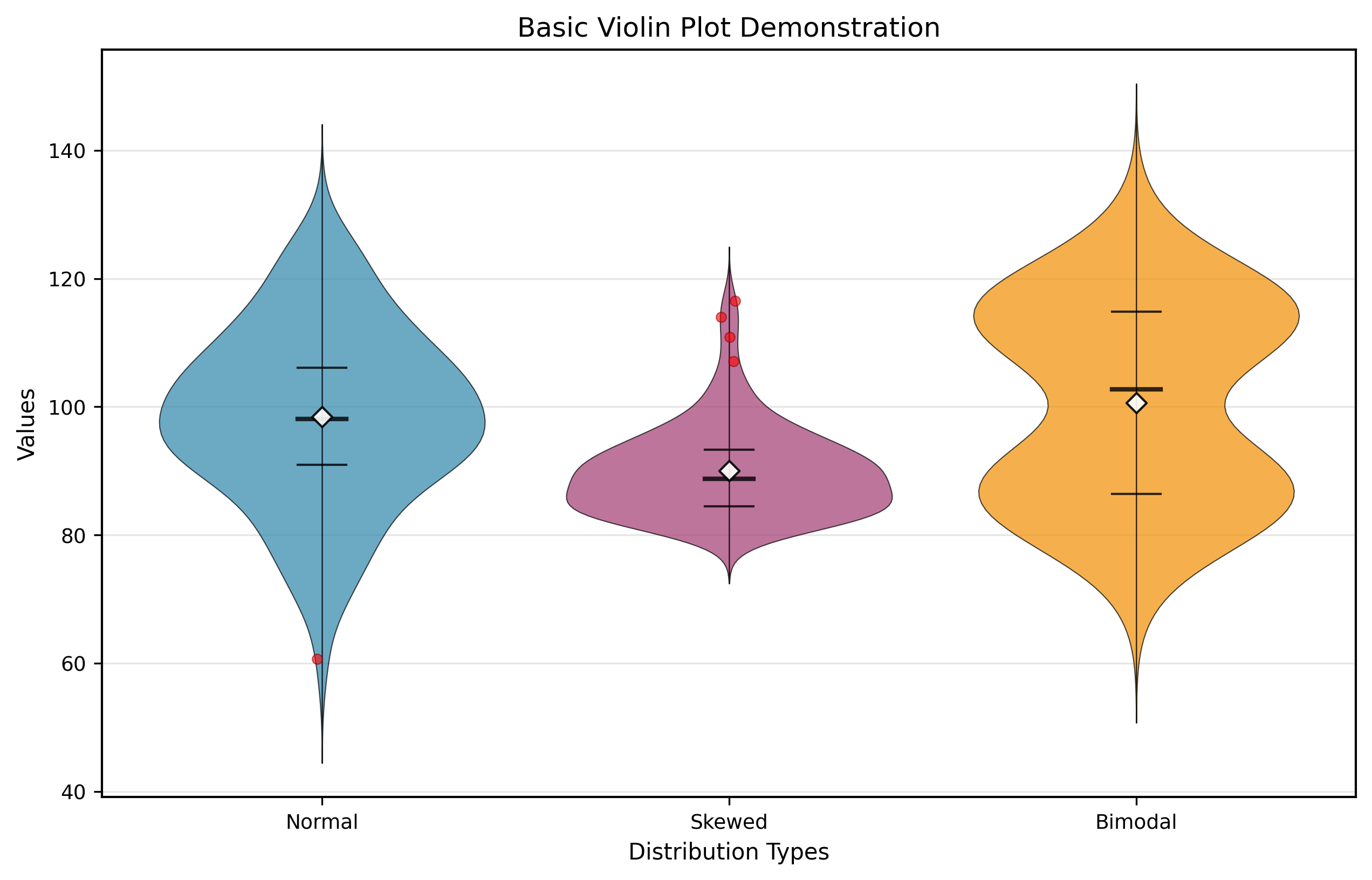
基础小提琴图

基础小提琴图展示了数据的密度分布和统计摘要，左右对称的设计便于比较不同组别的分布特征。

统计增强小提琴图

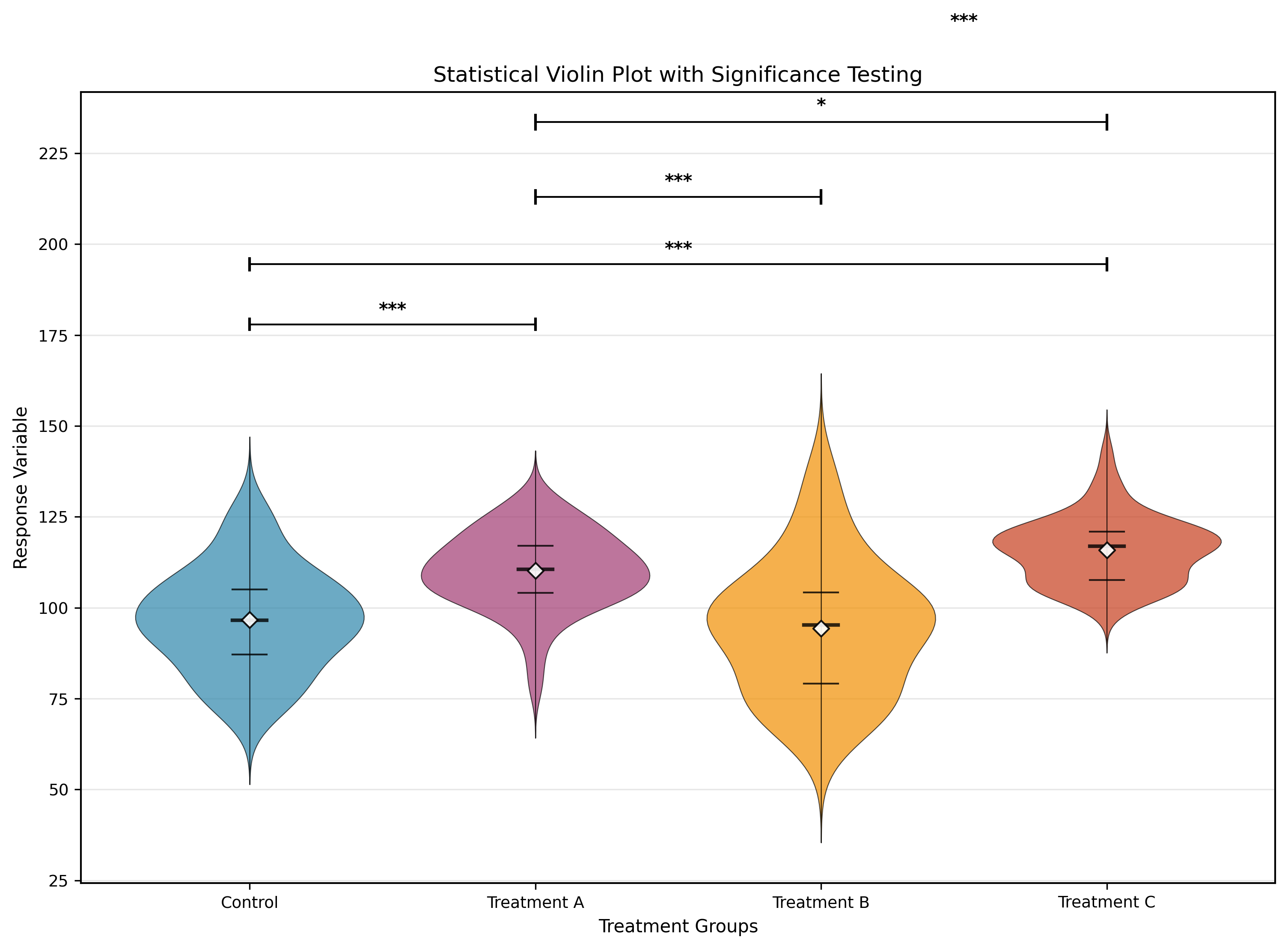
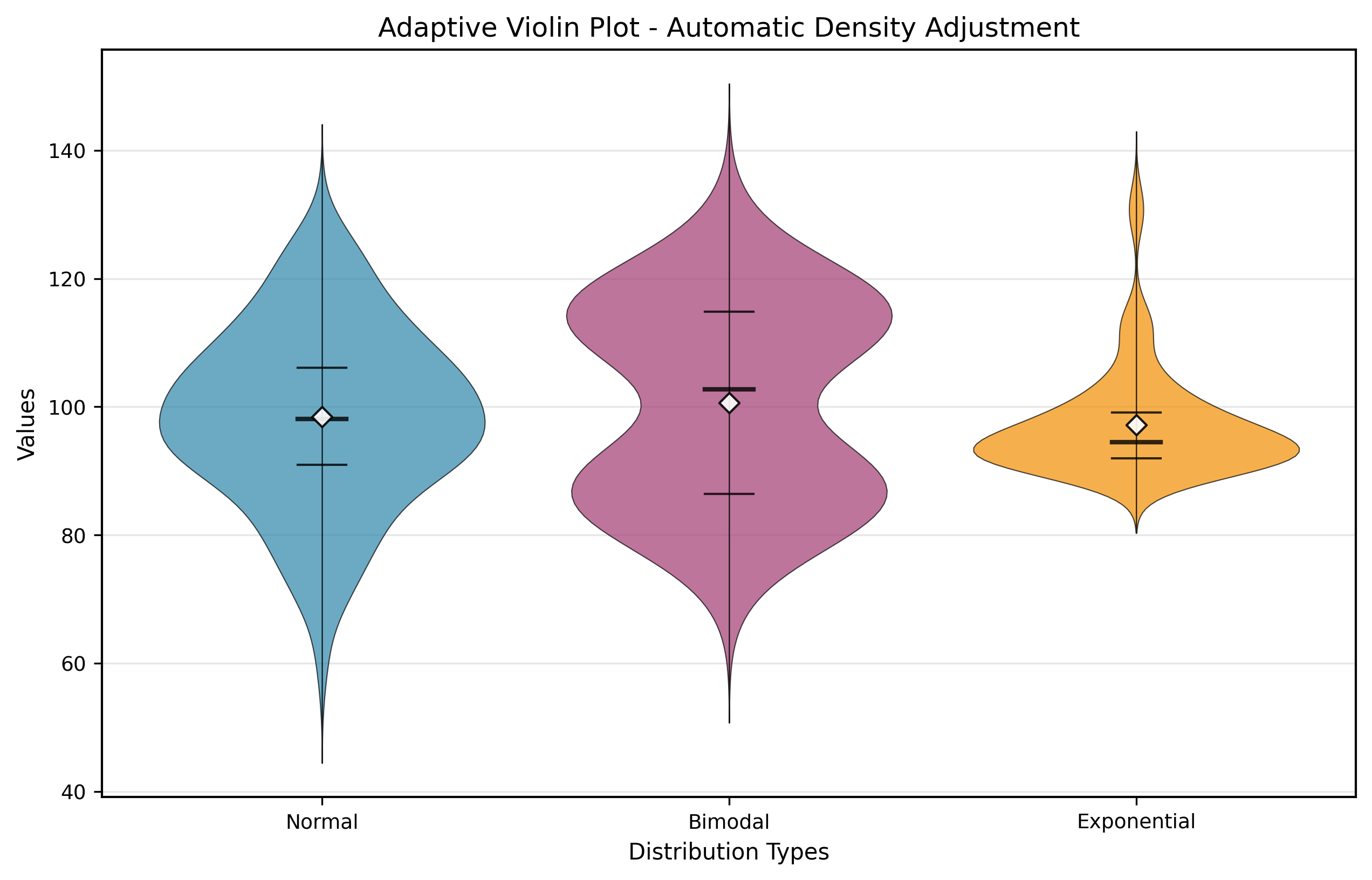
自适应小提琴图

根据数据的分布特征（正态、偏斜、重尾等）自动调整颜色和带宽参数，为不同类型的数据提供最优的可视化效果。

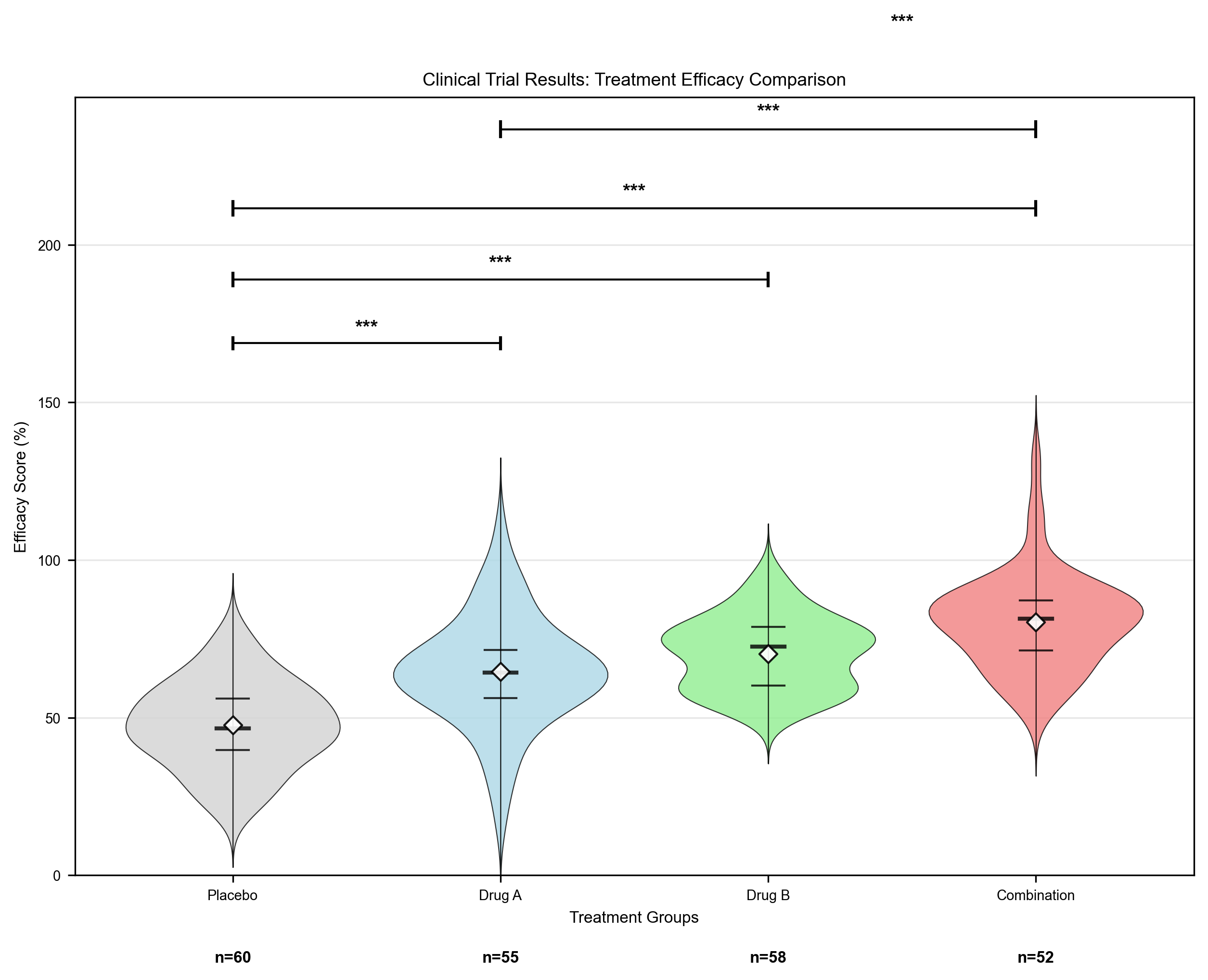
临床试验数据分析

实际临床试验数据的小提琴图展示，清晰对比了安慰剂、低剂量、高剂量和联合治疗组的响应分布差异。

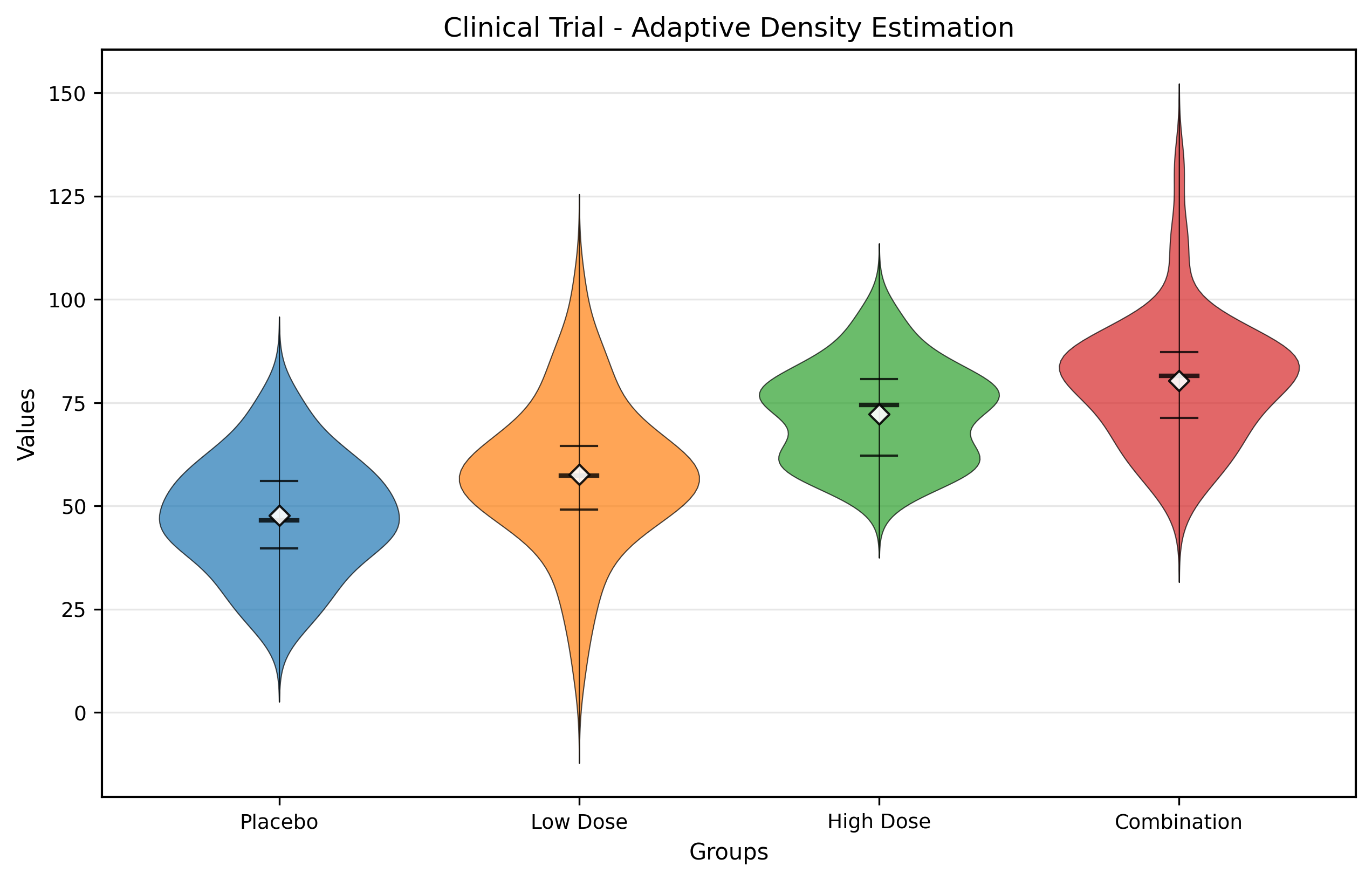
统计分析结果

以临床试验数据为例，程序自动生成详细的统计分析：

复制代码

Placebo: n=60, mean=47.68±13.63
Low Dose: n=55, mean=57.60±17.17
High Dose: n=58, mean=72.24±11.45
Combination: n=52, mean=80.35±14.92

该分析显示：

样本量差异：各组样本量在50-60之间
均值递增：从安慰剂组的47.68到联合治疗组的80.35呈递增趋势
变异性差异：低剂量组的标准差最大（17.17），显示较大的个体差异

使用说明

基本使用方法

安装依赖

bash 复制代码

pip install numpy matplotlib seaborn scipy pandas scikit-learn

创建小提琴图

python 复制代码

from violin_plot_generator import ViolinPlotGenerator

# 准备数据
data_groups = [
    np.random.normal(50, 10, 100),  # 组1
    np.random.normal(60, 15, 100),  # 组2
    np.random.normal(70, 8, 100)    # 组3
]
labels = ['Control', 'Treatment A', 'Treatment B']

# 创建生成器
generator = ViolinPlotGenerator(style='academic')

# 生成基础小提琴图
fig = generator.create_violin_plot(data_groups, labels, title="实验结果对比")

生成统计增强图

python 复制代码

# 生成带统计信息的图表
fig = generator.create_statistical_violin_plot(
    data_groups, labels,
    title="详细统计分析",
    filename="statistical_analysis.png"
)

高级配置

自定义样式

python 复制代码

# 演示文稿风格
generator = ViolinPlotGenerator(style='presentation', figsize=(14, 10))

# Web风格
generator = ViolinPlotGenerator(style='web')

带宽调整

python 复制代码

# 手动指定带宽
fig, ax = plt.subplots()
violin_parts = ax.violinplot(data_groups, bw_method=0.1)  # 小带宽
violin_parts = ax.violinplot(data_groups, bw_method='scott')  # Scott法则

颜色自定义

python 复制代码

# 自定义颜色方案
colors = ['#FF6B6B', '#4ECDC4', '#45B7D1', '#96CEB4']
for i, pc in enumerate(violin_parts['bodies']):
    pc.set_facecolor(colors[i % len(colors)])

最佳实践

数据准备

样本量：每组至少30个样本以获得可靠的密度估计
数据类型：适用于连续数值型数据
异常值处理：小提琴图对异常值不敏感，但仍建议检查

图表设计

组数限制：建议不超过5-7组，便于对比
刻度设置：确保y轴范围覆盖所有数据
标签清晰：组标签简洁明了

统计解读

分布形状：观察小提琴的宽度变化
集中趋势：注意中位数和均值位置
变异程度：比较小提琴的宽度
异常检测：查看箱线图外的点

总结与扩展

核心知识点总结

核密度估计：理解KDE算法和带宽选择
统计可视化：掌握分布特征的可视化方法
多组对比：学会有效比较多组数据分布
自适应调整：根据数据特征优化图表参数
科研应用：符合学术出版标准的图表制作

实用价值

小提琴图在科研和数据分析中的价值：

分布探索：快速了解数据分布特征
组间对比：直观比较不同条件下的数据差异
异常检测：识别数据中的异常模式
结果展示：学术论文和报告的专业图表

扩展方向

理论深化

高级密度估计
- 非参数密度估计
- 混合模型密度估计
- 条件密度估计
统计检验集成
- ANOVA检验可视化
- Kruskal-Wallis检验
- 多重比较校正
交互式功能
- 动态带宽调整
- 实时统计计算
- 交互式探索

应用扩展

生物信息学
- 基因表达分布比较
- 蛋白质丰度分析
- 单细胞测序数据可视化
临床研究
- 治疗效果分布分析
- 患者分组特征比较
- 生存数据可视化
金融分析
- 资产收益分布比较
- 风险度量可视化
- 投资组合分析
质量控制
- 制造过程变异分析
- 产品质量分布监控
- 过程能力指数可视化

学习建议

从基础开始：先掌握matplotlib的基础小提琴图绘制
理解密度：深入学习核密度估计的原理和参数
实践应用：使用真实数据进行练习
对比学习：将小提琴图与箱线图、直方图进行对比
工具选择：根据需求选择matplotlib或seaborn

通过本项目的学习，读者不仅掌握了小提琴图的绘制技巧，更重要的是理解了统计分布可视化的精髓，为各类数据分析任务提供了强大的可视化工具。小提琴图作为现代数据可视化的重要组成部分，在科研和商业分析中都有着不可替代的作用。

数据可视化 | Violin Plot小提琴图Python实现 数据分布密度可视化科研图表

引言

理论基础

小提琴图的构成要素

核密度估计

带宽选择

统计意义

代码实现

环境配置

核心小提琴图类实现

可视化效果展示

基础小提琴图

统计增强小提琴图

自适应小提琴图

临床试验数据分析

统计分析结果

使用说明

基本使用方法

高级配置

自定义样式

带宽调整

颜色自定义

最佳实践

数据准备

图表设计

统计解读

总结与扩展

核心知识点总结

实用价值

扩展方向

理论深化

应用扩展

学习建议

数据可视化 | Violin Plot小提琴图Python实现数据分布密度可视化科研图表