transformers音频实战01-音频概念

音频AI概念

1.1 音频的基本概念

将声音（物理振动）以可记录、可处理的形式呈现出来的方法。它分为 "模拟表示" 和 "数字表示" 两大类别，"波纹" 只是模拟表示中最直观的一种视觉化形式，无法涵盖音频表示的全部。

模拟表示的核心逻辑是 "物理量与声波振动直接对应"，常见形式有 3 种：

物理振动本身：比如唱片的凹槽（凹槽的深浅、疏密对应声波的振幅和频率）、磁带的磁信号（磁粉的磁化强度对应振幅）------ 这是 "看不见的模拟表示"，需要设备（唱针、磁头）还原成声音。
波形图（你说的 "波纹"） ：这是最直观的视觉化模拟表示 。它用 "横轴（X 轴）表示时间"，"纵轴（Y 轴）表示声波的振幅（音量大小）"，把连续的声波振动画成一条平滑的曲线（比如音频软件里看到的波形）。
例：你在手机录音 APP 里看到的 "动态波纹"，就是实时将麦克风捕捉的声波振动，转化为可视化的波形图 ------ 它能直观体现 "什么时候声音大（波峰高）、什么时候声音小（波峰低）"，但无法直接被计算机处理。
电信号：麦克风将声波振动转化为 "连续变化的电压信号"（振幅对应电压高低，频率对应电压变化速度），这个电信号也是模拟表示，需要通过 "模数转换" 才能变成数字信号。

模拟表示音频

想象一下你在水面上扔一块石头：

波纹：石头激起的波纹就像声波
振幅：波纹的高度 → 对应声音的音量（大声/小声）
频率：波纹的密集程度 → 对应声音的音调（高音/低音）

下面来回顾下波的一些概念。

波纹

想象一下，当你把一块石头扔进平静的湖面时，水面上会产生一圈圈向外扩散的涟漪。这些涟漪就是水波纹，声音的波纹（声波）也是类似的道理。

产生原因：当你说话、弹吉他或拍手时，物体会振动，从而挤压周围的空气。这种挤压会使空气产生疏密相间的变化。
传播过程：这种空气的疏密变化，会像湖面的涟漪一样，一圈一圈地向四面八方传播出去。
被我们接收：当这些"空气的涟漪"传播到我们的耳朵里，撞击耳膜，耳膜也会跟着同样地振动。我们的大脑再将这种振动翻译成声音。

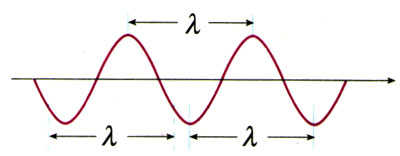
波长（λ）

波长（λ）是从一个波的一点到下一个波的同一点的物理长度，也就是在一个完整的振动周期内传播的距离。可以简单理解为相邻两个波峰之间（或者两个波谷之间）的距离，波长的国际单位是米。

频率（f）

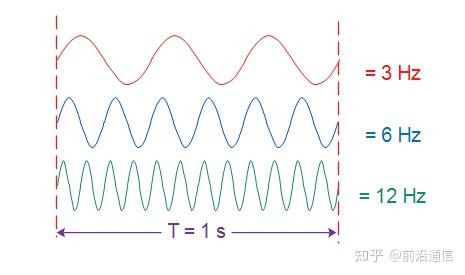
频率，就是物体振动的"快慢"。它直接决定了我们听到声音的音高（是尖锐还是低沉）。

频率是在一个时间单位里发生多少次（每 "1s"）。

频率的单位是赫兹，简称Hz。它的定义非常简单：
1 Hz = 每秒钟振动1次

如果某个声音的频率是 440 Hz：这意味着声源每秒钟来回振动了 440 次。这是音乐中的标准音高"La"（A4）。
如果某个声音的频率是 50 Hz ：这意味着声源每秒钟只振动了 50 次。这是一种很低沉的声音。

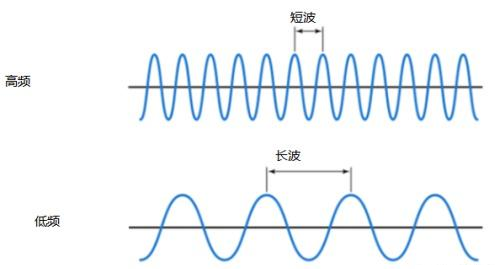
长波=低频

短波=高频（在同一时间帧内有更多的波）

常用单位及其换算
千赫兹（kHz）：1 kHz = 1000 Hz。
兆赫兹（MHz）：1 MHz = 1000 kHz = 1,000,000 Hz。
吉赫兹（GHz）：1 GHz = 1000 MHz = 1,000,000,000 Hz。

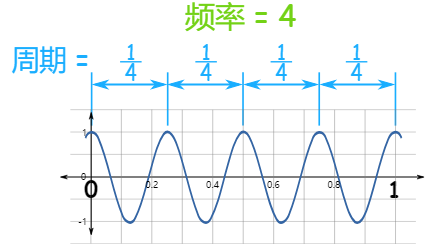
周期(T)

发生一次所需要的时间，假设频率2Hz 表示2个/s，周期就是：1个就是0.5s：

T=1/f 或者f=1/T

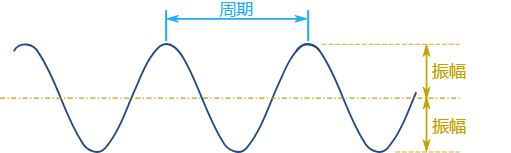
振幅

振幅是从中（平）线到最高点的高度（或到最低点），也是从最高点到最低点的距离除以2。

强度

频率的 "强度"：指该频率振动的 "幅度整体强弱"（对应音量）

声音的本质是 "空气的振动"，可以用一个 "正弦波" 描述：

要理解 " 频率为何能求出一个强度"，核心是区分 "瞬时幅度"（每个时间点的振动大小）和 "强度"（对振动 "整体强弱" 的量化描述）------ 强度本质是对无数个 "瞬时幅度" 的统计或整合结果，而非某一个时间点的数值。

用生活类比：比如你跑步时，"每一秒的速度"（如第 1 秒 5m/s、第 2 秒 6m/s）是 "瞬时速度"（对应 "瞬时幅度"）；而 "平均速度"（总路程 / 总时间）或 "最大速度" 是描述你跑步 "整体快慢" 的指标（对应 "强度"）------ 强度就是振动领域的 "整体强弱指标"。

以 2Hz（1 秒内 2 个完整波）的简谐振动 （最常见的振动形式，如音叉、纯音）为例，它的 "瞬时幅度" 随时间的变化是有规律的，遵循正弦 / 余弦函数：
瞬时幅度 A (t) = A₀ × sin (2πft)

其中：

f=2Hz（频率，决定 1 秒内波的数量）；
A₀是 "最大瞬时幅度"（振动的峰值，比如波的最高点到中间线的距离）；
t 是时间（如 0.0s、0.1s、0.2s...）。

当我们计算 "强度" 时，本质是对这个 "随时间变化的瞬时幅度" 做 "时间平均" 或 "能量整合"，因为：

人耳 / 仪器感知 "音量" 时，不会区分 "某一瞬间的幅度"，而是感知 "一段时间内的平均强弱"（比如你听一个 2Hz 的声音，不会觉得 "这一瞬间响、下一瞬间轻"，而是觉得 "整体有一个固定的音量"）；
物理上，"强度" 的本质是振动的能量密度（或功率），而能量与 "幅度的平方" 成正比，因此需要计算 "瞬时幅度平方的时间平均值"（专业上叫 "均方幅度"），再进一步推导为强度。

用具体数值验证（以 2Hz 简谐振动为例）

假设这个 2Hz 振动的 "最大瞬时幅度 A₀=10（单位可忽略）"，我们取 1 秒（刚好包含 2 个完整波）来计算，看看 "瞬时幅度" 如何整合为 "强度"：

时间 t（秒）	瞬时幅度 A (t)=10×sin (2π×2×t)	瞬时幅度的平方 A (t)²
0.00	10×sin(0)=0	0
0.125	10×sin(π)=0	0
0.25	10×sin(2π)=0	0
0.0625	10×sin(π/2)=10	100
0.1875	10×sin(3π/2)=-10	100（平方后负号消失）
0.3125	10×sin(5π/2)=10	100

接下来计算 "1 秒内瞬时幅度平方的平均值"（均方幅度）：

由于简谐振动的 "幅度平方" 在一个周期内的平均值是 A₀²/2（数学上可通过积分证明），对于 A₀=10 的振动，均方幅度 = 10²/2=50。

而物理上，强度与均方幅度成正比（若考虑声波，强度还与介质密度、声速等有关，但核心是 "均方幅度决定强弱"）------ 因此这个 2Hz 的振动，无论每个时间点的瞬时幅度如何变，其 "强度" 都由这个 "均方幅度（50）" 决定，最终表现为一个固定值。

什么样的频率下算一个强度

要理解 "什么样的频率下算一个强度"，核心结论是：与频率的具体数值（比如 2Hz、100Hz、1000Hz）无关 ------ 任何单一、稳定的频率（或频率成分固定的组合），都能通过整合其 "瞬时幅度" 得到一个对应的 "强度"。

关键不是 "频率多大"，而是 "频率是否稳定、是否为可被整合的'单一振动单元'"。下面从 "本质逻辑" 和 "实际场景" 两方面拆解，帮你彻底理清：

首先要打破一个误区：不是 "某个频率范围对应一个强度"，而是 "一个稳定的振动（无论频率是多少），都有一个描述其整体强弱的强度"。

可以把 "频率" 和 "强度" 理解为振动的两个独立 "维度"：

频率：描述振动的 "快慢"（1 秒内振动多少次，如 2Hz 慢、1000Hz 快）；
强度：描述振动的 "强弱"（振动的能量 / 幅度整体有多大，如小声、大声）。

就像 "汽车的速度（对应频率）" 和 "汽车的重量（对应强度）"------ 无论车速是 50km/h 还是 120km/h，每一辆稳定行驶的汽车都有一个固定的重量；同理，无论振动频率是 2Hz（如地震的低频振动）还是 2000Hz（如钢琴的中高音），每一个稳定的振动都有一个对应的强度。

比如：

2Hz 的地震波：频率慢，若振动幅度大（瞬时幅度的整合结果高），则强度大（破坏性强）；若幅度小，则强度小（几乎无感）；
1000Hz 的纯音：频率快，若扬声器振动幅度大（瞬时幅度整合结果高），则强度大（音量大）；若幅度小，则强度小（音量小）。

两种核心场景：帮你判断 "何时能算一个强度"

判断的关键是看 "振动的频率成分是否稳定、是否可被视为'一个整体'"，常见有两种场景：

场景 1：单一频率（纯音 / 纯振动）------ 必然对应一个强度

这是最基础的情况，比如你之前提到的 2Hz，或是收音机发出的 "纯蜂鸣音"（如 1000Hz）、音叉振动（如 440Hz 标准音）。

这类振动的特点是：频率只有一个，且不随时间变化，其 "瞬时幅度" 会按固定规律（正弦 / 余弦）波动（比如 0.0s 幅度 0、0.0625s 幅度 10、0.125s 幅度 0......）。

无论这个单一频率是 1Hz（极慢）还是 20000Hz（人耳上限），只要它稳定存在，就能通过 "整合瞬时幅度"（计算均方幅度、能量）得到一个固定的强度 ------ 因为它的 "强弱" 是统一的，没有其他频率干扰。

场景 2：多个频率组合（复合振动）------ 可按 "频率分组" 算多个强度，或算 "总强度"

现实中大部分振动是多个频率的组合，比如人的声音、音乐、机器噪音。这时 "强度" 的计算更灵活，但核心逻辑不变：每个稳定的频率成分，都能单独算一个强度；也能把所有频率的强度加起来，算 "总强度"。

举个例子：钢琴弹一个 "和弦"（比如 C 和弦，包含 261.6Hz、329.6Hz、392Hz 三个主要频率）。

单独看：261.6Hz 的振动有一个强度（对应这个低音的音量），329.6Hz 的振动有一个强度（对应中音的音量），392Hz 的振动也有一个强度（对应高音的音量）；
整体看：把这三个频率的强度相加，就能得到这个和弦的 "总强度"（对应你听到的 "和弦整体音量"）。

再比如 "白噪音"（包含人耳能听到的所有频率，20Hz-20000Hz）：

可以按 "频率段" 算强度（比如 20-200Hz 低频段的强度、200-2000Hz 中频段的强度、2000-20000Hz 高频段的强度），用来分析噪音的 "频率分布"（比如低频噪音多还是高频噪音多）；
也可以算 "总强度"（所有频率段强度之和），用来描述 "噪音整体有多吵"。

反例：什么时候 "无法算一个固定强度"？------ 频率不稳定 / 无规律时

如果振动的频率本身是 "变化的、无规律的"，那么它的 "强度" 也会随频率变化而波动，无法用一个固定值描述。但这不是 "频率多大" 的问题，而是 "频率是否稳定" 的问题。

比如：

汽车加速时的发动机噪音：频率从低到高持续变化（转速升高，频率变大），同时振动幅度也在变，因此 "强度" 会随时间波动，无法说 "这个噪音对应一个强度"，只能说 "某一时刻（对应某一频率）的强度是多少"；
杂乱的工地噪音：频率成分随时变化（一会儿是锤子敲打的高频，一会儿是卡车启动的低频），且每个频率的幅度也不稳定，因此也无法用一个固定强度描述，只能用 "平均强度" 或 "最大强度" 来大致衡量。
如何区分采样语音的 "频率稳定 / 不稳定""有规律 / 无规律"？

语音信号的本质是非平稳信号（频率成分随时间变化，比如说话时 "a""o" 的频率不同），但 "不稳定" 和 "无规律" 有明确判断标准 ------ 核心是看 "频率成分的变化是否可预测、是否符合语音的生理发声规律"。

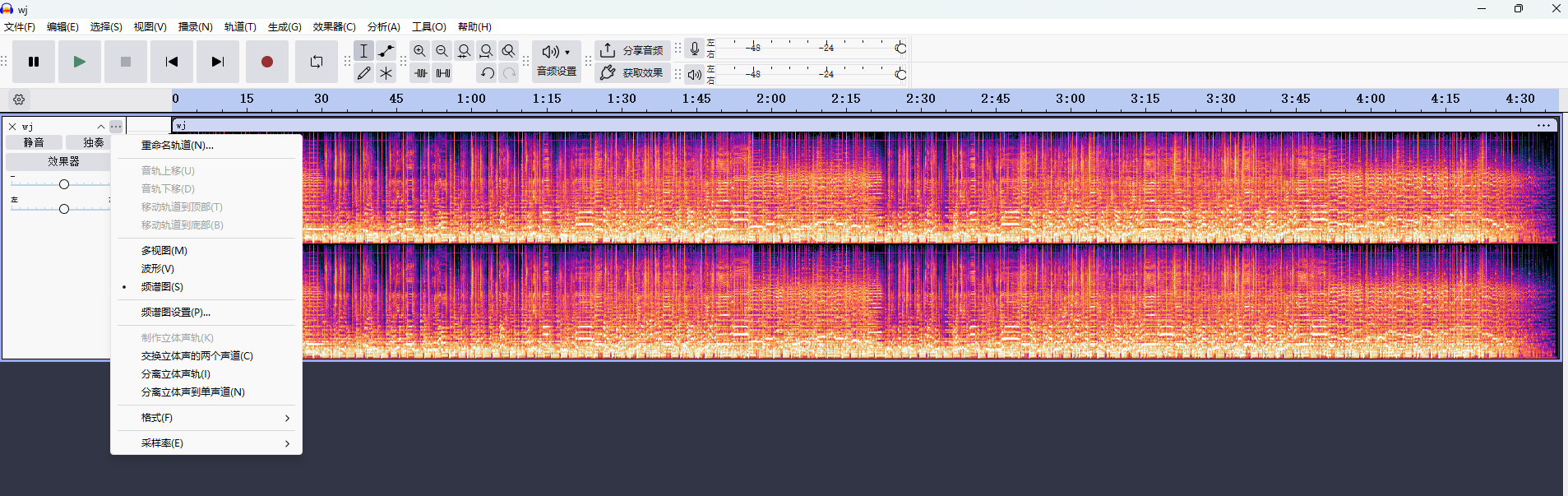
具体通过时频分析工具实现，最常用的是 "短时傅里叶变换（STFT）"，它能将一维的 "时间 - 幅度" 采样信号，转化为二维的 "时间 - 频率 - 能量" 图谱（俗称 "语谱图"），直观展示频率随时间的变化。

无需复杂编程，用开源工具就能观察：

入门级：Audacity（免费音频编辑软件）------ 导入采样语音后，用 "频谱分析" 功能生成语谱图，直观观察频率分布；
专业级：MATLAB/Python（ librosa 库）------ 通过librosa.stft()函数计算 STFT，再用librosa.display.specshow()绘制语谱图，量化分析频率随时间的变化率。

波速

波长：波在一个完整的振动周期内传播的距离。可以简单理解为相邻两个波峰之间的距离。
- 单位：通常是米。
频率：波每秒钟振动的次数。
- 单位：赫兹。1 Hz 就是每秒振动1次。
- 它代表波的"忙碌程度"。
波速：波在特定介质中传播的速度。
- 单位：米/秒。
- 关键点 ：波速只由介质本身决定，与频率和波长无关。例如，在室温空气中，声速大约是 343 米/秒；而在水中，声速会快得多，约 1500 米/秒。

想象一下你在跑道上跑步：

频率：你的步频，即每秒迈出多少步。
波长：你的步幅，即每一步跨出的距离。
波速：你的跑步速度。

你的跑步速度（波速） = 步频（频率） × 步幅（波长）

这个公式 Velocity（波速） = Frequency（频率） × Wavelength（波长） 是上面那个公式的变形，但意思完全一样。

数字表示音频

声音数字化的两个核心概念：采样率（Sample Rate）和位深（Bit Depth）

python 复制代码

# 用生活例子理解采样率：
# 假设你要记录一个人的跳舞动作，用图像的例子更形象：

低采样率（8kHz） = 每秒拍8张照片 → 只能看到大概动作
高采样率（44.1kHz） = 每秒拍44100张照片 → 能看到每个细微动作

# 位深好比照片的清晰度：
8位深 = 用8种颜色描述动作 → 轮廓清晰
16位深 = 用65536种颜色描述 → 细节丰富

1. 采样率 - 关于时间的"保真度"

生活例子： 想象你在用手机录一段很快的"哒哒哒"的机关枪声音。
- 低采样率（8kHz）： 就像你每隔1/8000秒才记录一个声音点。对于快速的枪声，你可能会漏掉很多单个的"哒"声，录下来的声音可能变成一片模糊的"嗡鸣声"，丢失了原始声音的节奏和尖锐感。
- 高采样率（44.1kHz）： 就像你每隔1/44100秒就记录一个点。这样你就能捕捉到每一个快速的"哒"声，还原出逼真、清晰的机关枪音效。
核心作用： 采样率决定了音频文件的频率范围（高音能到多高）。根据奈奎斯特定理，最高能录制和还原的频率是采样率的一半。44.1kHz的采样率可以记录最高22.05kHz的声音，这刚刚超过人耳的听觉极限（20kHz）。

想象一下你要用相机记录一个旋转的风扇：

风扇的转速 相当于声音的频率。
你拍照的速度 相当于 采样率。

情况一：拍照速度足够快（高采样率）
- 如果你的拍照速度比风扇叶片的旋转速度快很多，你拍下的连续照片连起来看，就能清晰地还原出风扇旋转的动态，甚至能数出有几个叶片。这说明你成功记录了高频信息。
情况二：拍照速度太慢（低采样率）
- 如果你的拍照速度和风扇转速差不多，甚至更慢，你就会发现一个奇怪的现象：在连续的照片中，风扇看起来可能转得很慢、静止，甚至像是在倒转！这完全扭曲了真实的运动。

在数字音频中，第二种情况导致的扭曲现象被称为混叠。

奈奎斯特-香农采样定理与混叠

这是理解两者关系的数学基础。

定理内容 ：要准确还原一个频率为 f 的信号，采样率必须至少是 2f。
奈奎斯特频率：这个可记录的最高频率（采样率 / 2）就被称为奈奎斯特频率。

为什么是 2 倍？

因为要定义一个正弦波（最简单的频率），你至少需要两个点：一个点捕捉波峰，一个点捕捉波谷。少于两个点，你就无法确定波的频率和形状。

例如，CD的44.1kHz采样率，最高能记录 44100 / 2 = 22050 Hz 的声音。这个频率已经远超普通人耳的听力上限（约20000 Hz），所以完全够用了

如果采样率不满足定理，会发生什么？

假设用 800Hz 采样率记录 440Hz 声音（800 < 2×440=880，不满足定理）：

此时会发生 "混叠"，440Hz 信号会被错误还原成 800 - 440 = 360Hz 的信号；

就像用每秒 800 张的速度拍每秒摆动 440 次的钟摆，由于拍照太慢，会误以为钟摆每秒只摆动 360 次（记录失真）。

注意常用的公式：

最高可还原频率 = 采样率 ÷ 2，上面的逻辑。
时长=样本总数/采样率
举例：如果一段音频有 32000 个采样点，采样率是 16000 Hz，那么时长就是 32000 ÷ 16000 = 2 秒。
采样间隔（秒）= 1 ÷ 采样率，两个相邻采样点之间的时间间隔。例如：
采样率 44.1kHz 时，采样间隔 = 1/44100 ≈ 0.00002267 秒（约 22.67 微秒），即每 22.67 微秒采集一个样本。

2. 位深 - 关于振幅的"精确度"

位深（如 16bit、24bit）描述的是：单个采样点的振幅信息，用多少个二进制位（Bit）来存储，位深越大能体现的精细度越高，分辨的声音模式越多。

小白解释： 位深就是每一张"声音照片"的精细程度，或者说它用了多少种"灰度"来记录音量的大小（存储使用二进制0和1）。

位深低（比如1位）： 只有纯黑和纯白两种颜色。记录声音时，音量要么是"巨响"（1），要么是"完全没声"（0）。这会产生巨大的噪音和失真，因为现实中的声音音量是连续变化的。
位深高（比如16位）： 有 2的16次方 = 65536 种不同的"灰度"来表示音量。从最轻的耳语到最响的爆炸声，它都能用这65536个精细的等级来准确记录。CD音质就是16位。
位深更高（24位）： 有 2的24次方 = 约1677万种等级！这让录音的动态范围极大，能同时记录下极其微弱和非常响亮的声音，而且背景噪音极低，专业录音都用这个。

生活例子： 想象你在调音量的旋钮，从完全无声（0）到最大声（100）。

低比特深度（8位 = 256级）： 这个旋钮只有256个档位。当你轻轻转动时，音量可能从第10档"咔哒"一下跳到第11档，中间没有平滑的过渡。在录音中，这会导致微小的声音细节被丢失，并且产生一种"数字化"的噪音（量化噪声）。声音听起来粗糙、有颗粒感。
高比特深度（16位 = 65，536级）： 这个旋钮有超过6万5千个档位。档位如此之多，以至于你转动它时，感觉是完全平滑的。它可以极其精确地记录下声音最细微的强弱变化，比如歌手从气息声到强音的平滑过渡，或者小提琴悠扬的尾音。动态范围更广，背景噪音极低。

核心作用： 位深决定了音频的动态范围（最轻和最响声音的差距）和精度。每一位大约提供6分贝的动态范围。16位深的理论动态范围是96dB，这已经非常接近CD品质了。

参数	在图像中的类比	在音频中的实际含义	核心决定因素
采样率	每秒拍摄的照片张数（时间上的连续性）	每秒采集的声音样本数	高频响应/带宽（声音能有多"尖"）
位深	每个像素可用的颜色数量（亮度/色彩的精度）	每个样本的振幅精度	动态范围/信噪比（声音细节的丰富度）

概念总结

术语	比喻	它决定了什么	常见值
波纹（声波）	要画的波浪线本身	声音的原始形状	-
振幅	波浪的高度	声音的音量/响度	-
采样率	每秒拍的照片数量	声音的频率范围（高音保真度）	44.1 kHz (CD), 48 kHz (视频), 96 kHz (高清音频)
位深	测量波浪高度的尺子的精确度	声音的动态范围和清晰度（噪音水平）	16-bit (CD), 24-bit (录音/母带)

一个综合例子：

录制一段 CD 质量的音乐（16-bit / 44.1 kHz）：

声波（波纹）传入麦克风，其振幅大小决定了音量。
音频接口每秒对声波进行 44,100 次 采样（采样率）。
每次采样时，用一个精确到 65,536 个等级的尺子（16-bit 位深）来测量此刻声波的振幅值，并转换成一个二进制数字。
所有这些数字连在一起，就构成了我们听到的数字音频文件。

易错点

频率，采样点混淆

频率（Hz）不是 "1 秒有多少个点"，而是 "1 秒内振动的次数"；而 "强度" 则是指振动的 "幅度大小"（对应声音的音量）。这两个概念完全不同，我们一步步拆解

先厘清：频率 ≠ 采样率（你混淆的核心

采样率（Sample Rate）：单位是 Hz，但含义是 "1 秒内采集的音频点数"（比如 16000Hz=1 秒采 16000 个点），这是 "记录声音的精度"，和声音本身的特性无关；
频率（Frequency）：单位也是 Hz，但含义是 "声音信号 1 秒内的振动次数"（比如 440Hz=1 秒振动 440 次），这是 "声音本身的音调高低"，和采样率无关。

举个例子：用 16000Hz 采样率记录 440Hz 的声音，就像 "用每秒拍 16000 张照片的速度，拍摄一个每秒摆动 440 次的钟摆"------ 采样率是 "拍照速度"，频率是 "钟摆摆动速度"，两者完全不同。

1.2 音频分类是什么？

生活化理解：就像教小朋友识别不同的声音

听到"汪汪" → 知道是狗狗
听到"叮咚" → 知道是门铃
听到"哗啦啦" → 知道是下雨

技术定义：让AI模型自动判断一段音频属于哪个预定义的类别。

1.3 模型如何"听"懂声音？

人类的听觉过程：

耳朵接收声波
耳蜗将不同频率的声音分离
大脑识别模式（这是说话声？音乐声？）

AI的"听觉"过程：

波形图 → 原始的声波记录

text 复制代码

[振幅, 振幅, 振幅, ...] # 一长串数字

频谱图 → AI的"听力图"
- 横轴：时间
- 纵轴：频率
- 颜色亮度：音量大小
梅尔频谱图 → 更接近人耳感知的"听力图"
- 对人耳敏感的低频区分辨更细
- 对不敏感的高频区分辨较粗

1.4 深度学习模型的工作原理

比喻：教AI认声音就像教小朋友认动物

训练阶段：

text 复制代码

给小朋友看：🐕 + 说"这是狗"
           🐱 + 说"这是猫"
           🐦 + 说"这是鸟"

推理阶段：

text 复制代码

小朋友看到新动物：🐕 → "这是狗！"

AI的工作流程：

python 复制代码

# 1. 准备"教材"（数据集）
音频文件 + 标签（如："狗叫", "猫叫"）

# 2. "学习"过程（训练）
模型分析成千上万个音频，学习模式

# 3. "考试"（推理）
新音频 → 模型 → 预测结果

实践案例 - 带着理解去编码

案例1：初识音频分类 - 使用现成的智能工具

数据集介绍：SUPERB关键词识别数据集

内容：人们说简单关键词的录音
关键词：yes, no, up, down, left, right等35个词
用途：测试模型是否能识别语音命令

核心关键词（语音命令）

这些是数据集中的主要识别目标，通常包括日常简单指令，例如：

yes（是）
no（否）
up（上）
down（下）
left（左）
right（右）
on（开）
off（关）
stop（停止）
go（开始）

特殊标签

除了上述核心关键词，数据集中还包含两个特殊标签用于区分非目标音频：

_silence_：表示静音片段（无有效声音）。
_unknown_：表示音频中存在声音，但不属于上述核心关键词（例如其他未标注的词汇或噪音）。

模型介绍：HuBERT-base模型

特点：像是一个受过听力训练的专业人士
能力：能理解音频的上下文含义
应用：智能音箱、语音助手

环境安装：

这里依然使用uv进行python项目管理

安装依赖包

复制代码

uv add torchaudio torchcodec ffmpeg matplotlib

默认音频加载需要用到torchcodec，并且调用ffmpeg所以要提前下载ffmpeg，下载地址

https://www.gyan.dev/ffmpeg/builds/

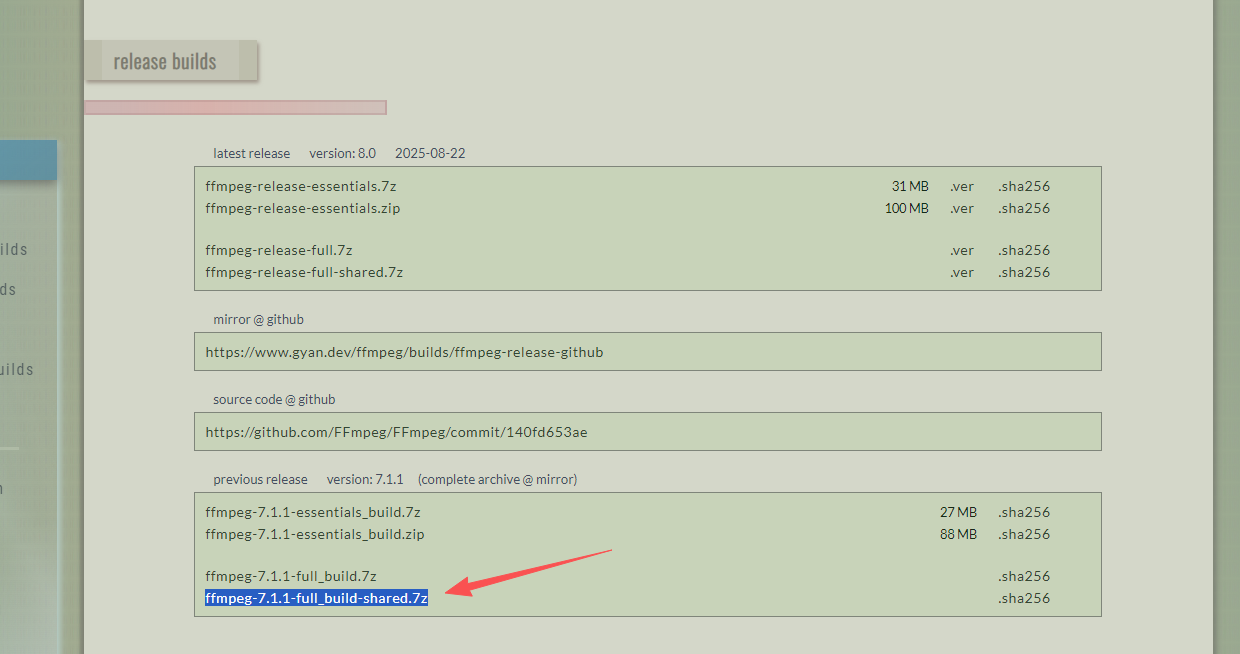
到目前位置torchcodec 只支持ffmpeg4-7 不要下载太新的版本，比如我下载的是

ffmpeg-7.1.1-full_build-shared.7z，注意下载full-shared版本有动态链接库dll

安装/修复 VC++ 运行库（最关键）

去微软官方下载最新版：https://aka.ms/vs/17/release/vc_redist.x64.exe

装完重启，再试加载。

可以尝试编写一个案例用于测试加载，因为很多时候都会报错

注意我这里ffmpeg目录虽然是8.0但是我里面的内容是7，之前用8.0走了太多弯路

torchcodec是使用libtorchcodec_core7.dll加载ffmpeg7所以我们可以先手动尝试加载看是否报错

复制代码

import os, ctypes

# 告诉 Python 去 torch\lib 目录找 DLL
torch_lib_path = r"D:\code\audio\.venv\Lib\site-packages\torch\lib"
os.add_dll_directory(torch_lib_path)

# 如果你自己下了 ffmpeg，把 bin 路径也加上
ffmpeg_bin_path = r"D:\green\ffmpeg-8.0-essentials_build\bin"
os.add_dll_directory(ffmpeg_bin_path)

# 尝试加载 torchcodec 的 DLL
dll_path = r"D:\code\audio\.venv\Lib\site-packages\torchcodec\libtorchcodec_core7.dll"
ctypes.CDLL(dll_path)

print("✅ DLL 加载成功")

因为ffmpeg会依赖torch和ffmpeg包

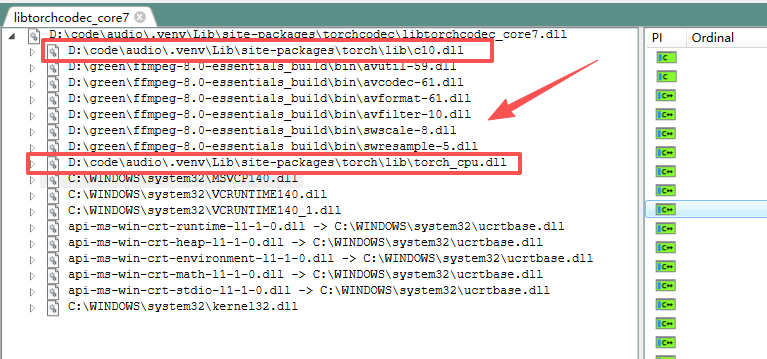
如果依然出现错误

复制代码

FileNotFoundError: Could not find module 'D:\code\audio\.venv\Lib\site-packages\torchcodec\libtorchcodec_core7.dll' (or one of its dependencies). Try using the full path with constructor syntax.

那就安装个depend去查看下libtorchcodec_core7.dll下是否还有dll没有。

一步一步编码学习：

复制代码

# 第一步：导入工具包
from transformers import pipeline  # 这是Hugging Face的"智能工具箱"
from datasets import load_dataset  # 用于加载标准数据集
import os, ctypes
# 这个一定要手动设置，否则可能会出错，如果需要加torch也一样的加
ffmpeg_bin_path = r"D:\green\ffmpeg-8.0-essentials_build\bin"
os.add_dll_directory(ffmpeg_bin_path)
print("🎯 学习目标：了解如何使用现成的AI工具进行音频分类")

# 第二步：创建一个音频分类器（就像买一个智能音箱）
print("\n1. 创建音频分类器...")
classifier = pipeline(
    "audio-classification",
    model="superb/hubert-base-superb-ks"
)
print("✅ 分类器创建成功！就像买了一个能听懂命令的智能音箱")

# 第三步：获取测试数据（就像准备测试题目）
print("\n2. 加载测试音频...")
dataset = load_dataset("Codec-SUPERB/superb_ks", split="original[:3]")  # 只取前3个样本
print(f"✅ 加载了 {len(dataset)} 个测试音频")

# 第四步：逐个测试并分析结果
print("\n3. 开始测试模型...")
for i, sample in enumerate(dataset):
    print(f"\n--- 测试音频 {i + 1} ---")

    audio_data = sample["audio"]
    print(f"📊 音频信息：")
    print(f"   采样率：{audio_data['sampling_rate']} Hz")
    print(f"   时长：{len(audio_data['array']) / audio_data['sampling_rate']:.2f} 秒")

    # 让模型"听"这个音频并判断
    predictions = classifier(audio_data['array'])

    print(f"🎧 模型识别结果：")
    for j, pred in enumerate(predictions[:3]):  # 显示前3个最可能的结果
        print(f"   {j + 1}. 可能是 '{pred['label']}'，置信度：{pred['score']:.2%}")

print("\n✨ 实践总结：")
print("• 学会了使用pipeline快速创建音频分类器")
print("• 了解了如何加载和使用标准数据集")
print("• 看到了模型如何对音频进行分类预测")

输出

复制代码

1. 创建音频分类器...
✅ 分类器创建成功！就像买了一个能听懂命令的智能音箱

2. 加载测试音频...
Device set to use cpu
✅ 加载了 3 个测试音频

3. 开始测试模型...

--- 测试音频 1 ---
📊 音频信息：
   采样率：16000 Hz
   时长：1.00 秒
🎧 模型识别结果：
   1. 可能是 '_silence_'，置信度：100.00%
   2. 可能是 'left'，置信度：0.00%
   3. 可能是 '_unknown_'，置信度：0.00%

--- 测试音频 2 ---
📊 音频信息：
   采样率：16000 Hz
   时长：1.00 秒
🎧 模型识别结果：
   1. 可能是 '_silence_'，置信度：100.00%
   2. 可能是 'left'，置信度：0.00%
   3. 可能是 '_unknown_'，置信度：0.00%

--- 测试音频 3 ---
📊 音频信息：
   采样率：16000 Hz
   时长：1.00 秒
🎧 模型识别结果：
   1. 可能是 '_silence_'，置信度：100.00%
   2. 可能是 'left'，置信度：0.00%
   3. 可能是 '_unknown_'，置信度：0.00%

我们到数据集去查看前三个音频确实是静音片段

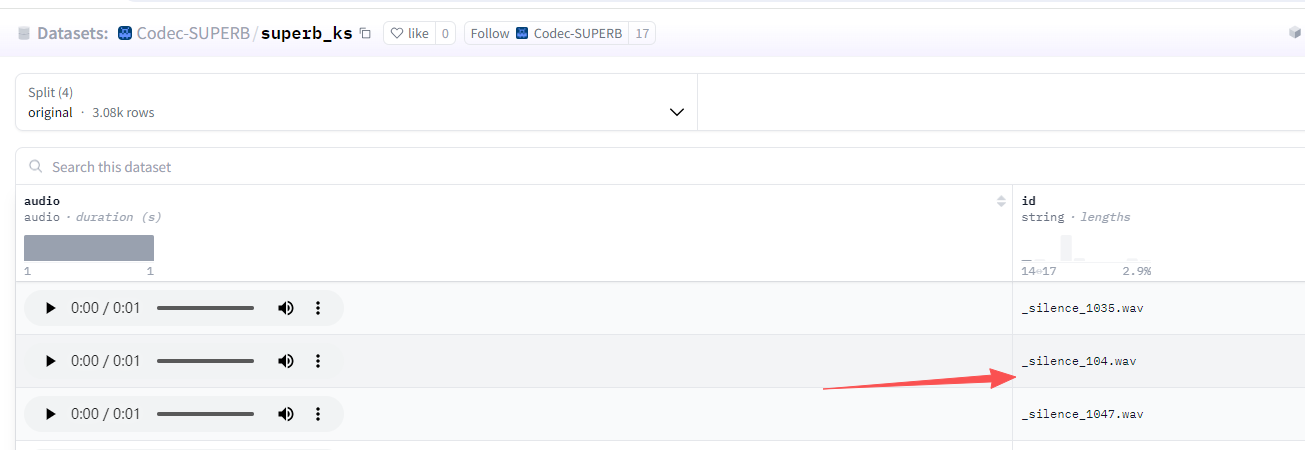
案例2：深入了解音频特征 - 看看AI的"眼睛"看到了什么

理论知识准备：

频谱图的重要性：就像医生看X光片一样，AI通过频谱图来"诊断"音频内容。

一步一步编码学习：

原始波形

以下这段代码生成的 "440Hz 纯音波形" 是一个音频信号处理的基础测试案例，用途就像数学中的 "1+1=2"、物理中的 "自由落体实验"------ 用最简单的场景理解复杂系统的核心原理。它的用途主要有 3 类，从 "学习理解" 到 "技术验证" 全覆盖：

最核心：学习音频信号的本质

音频（声音）的本质是 "随时间变化的振动信号"，而 440Hz 纯音是最简单的振动形式（单一频率、无杂音），适合用来直观理解：

声音的三要素：
- 频率（440Hz）→ 音调高低（A4 钢琴键的标准音）；
- 振幅（0.5）→ 音量大小（中等音量，避免失真）；
- 时长（2 秒）→ 声音持续时间。
数字音频的存储逻辑：
- 采样率（16000Hz）→ 每秒存 16000 个 "振动幅度"（就像用 16000 个点描述曲线）；
- 数组 pure_tone 里的 32000 个数值 → 就是这 2 秒内每个 "采样点" 的振动幅度（数字音频的本质就是这个数组）。
傅里叶变换的作用：
- 对这个纯音做傅里叶变换，会在 440Hz 处出现一个 "尖峰"（其他频率几乎为 0），直观验证 "傅里叶变换能拆解频率成分"；
- 对比 "复杂声音"（如人声）的频谱，能立刻理解 "复杂声音是多个纯音的叠加"。

代码：

复制代码

import torch
import torchaudio.transforms as T
import matplotlib.pyplot as plt
import numpy as np

# 中文配置
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False

print("🎯 学习目标：让音频特征图形更直观清晰")

# 1. 创建测试声音
sample_rate = 16000
duration = 2.0
t = np.linspace(0, duration, int(sample_rate * duration))

frequency = 440
pure_tone = 0.5 * np.sin(2 * np.pi * frequency * t).astype(np.float32)

waveform = torch.from_numpy(pure_tone).unsqueeze(0)  # (1, 32000)

# 2. 准备子图
fig, axes = plt.subplots(2, 2, figsize=(15, 10))

# --------------------------
# 2.1 原始波形
# --------------------------
plot_samples = 2000  # 展示前2000个点 ≈ 0.125s，能看到足够多周期
axes[0,0].plot(t[:plot_samples], pure_tone[:plot_samples], linewidth=1.5, color="darkorange")
axes[0,0].set_title('原始波形（前0.125秒）', fontsize=12)
axes[0,0].set_xlabel('时间 (秒)')
axes[0,0].set_ylabel('振幅')
axes[0,0].grid(True, alpha=0.4)
axes[0,0].set_ylim(-0.6, 0.6)

输出

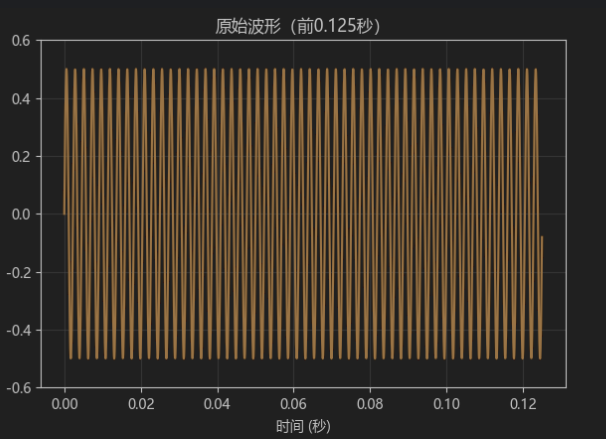
我们用具体数据一步步拆解这段代码的计算过程，从 "时间数组生成" 到 "波形生成"，再到 "PyTorch 张量转换"，用实际数值让每一步都清晰可见。

一、核心变量说明

先明确关键参数的含义和数值：

sample_rate = 16000：采样率（每秒采集 16000 个点）；
duration = 2.0：音频时长（2 秒）；
frequency = 440：声音频率（440Hz，每秒振动 440 次）；
最终生成的音频总点数 = 采样率 × 时长 = 16000 × 2 = 32000 个点。

二、第一步：生成时间数组 t（np.linspace 的计算）

代码：t = np.linspace(0, duration, int(sample_rate * duration))

作用：生成 32000 个从 0 到 2 秒的 "均匀时间点"，每个点对应一个采样时刻。

具体数据例子（取前 5 个和最后 1 个点）：

索引（第几个点）	时间值 `t`（秒）	计算逻辑（均匀间隔）
0	0.0	起点（第 0 秒）
1	~0.0000625	间隔 = 2 秒 / (32000-1) ≈ 0.0000625 秒（62.5 微秒）
2	~0.000125	0 + 2 × 间隔
3	~0.0001875	0 + 3 × 间隔
4	~0.00025	0 + 4 × 间隔
...	...	...
31999	2.0	终点（第 2 秒）

规律：每个点的时间 = 索引 × 间隔，间隔 ≈ 62.5 微秒（1/16000 秒，即采样周期）。

三、第二步：生成纯音波形 pure_tone（正弦波计算）

代码：pure_tone = 0.5 * np.sin(2 * np.pi * frequency * t).astype(np.float32)

作用：根据时间数组 t，计算每个时刻的声音振幅（0.5 是振幅，控制音量）。

正弦波公式拆解：

单个点的振幅 = 0.5 × sin (2π × 频率 × 时间)

2π × frequency × t：将 "时间" 转换为 "角度"（确保每秒振动 440 次）；
sin(...)：计算角度对应的正弦值（范围 [-1, 1]）；
0.5 × ...：将振幅压缩到 [-0.5, 0.5]（控制音量）。

具体数据例子（对应 t 的前 5 个点）：

索引	时间 `t`（秒）	角度 = 2π×440×t（弧度）	sin (角度)	振幅 = 0.5×sin (角度)	物理意义（声音状态）
0	0.0	0	0	0.0	振动起点（中间位置）
1	0.0000625	2π×440×0.0000625 ≈ 0.1727 弧度（≈9.9 度）	≈0.1719	≈0.0859	向上振动（小幅度）
2	0.000125	2π×440×0.00125 ≈ 0.3455 弧度（≈19.8 度）	≈0.3391	≈0.1696	继续向上振动
3	0.0001875	≈0.5183 弧度（≈29.7 度）	≈0.4932	≈0.2466	接近最高点
4	0.00025	≈0.6912 弧度（≈39.6 度）	≈0.6367	≈0.3183	向上振动中
...	...	...	...	...	...
1136	~0.071 秒	π/2（90 度）	1.0	0.5	振动最高点（音量最大）

关键规律：

每经过 1/440 ≈ 0.00227秒（440Hz 的 1/4 周期），角度增加 π/2，振幅从 0→0.5→0→-0.5→0，完成一次完整振动；
2 秒内共振动 440×2 = 880次，对应波形有 880 个完整周期。

四、第三步：转换为 PyTorch 张量 waveform

代码：waveform = torch.from_numpy(pure_tone).unsqueeze(0)

作用：将 NumPy 数组（pure_tone）转换为 PyTorch 张量，并增加 "通道维度"（音频通常需要通道信息）。

数据格式变化：

pure_tone 是 NumPy 数组，形状为 (32000,)（1 维数组，32000 个振幅值）；
torch.from_numpy(pure_tone) 转换为 PyTorch 张量，形状仍为 (32000,)；
.unsqueeze(0) 在第 0 维增加一个维度，最终形状为 (1, 32000)：
- 第 1 个维度 1：表示 "单通道音频"（如 mono 单声道）；
- 第 2 个维度 32000：表示 32000 个采样点的振幅值。

张量数据例子（前 5 个值）：

python 复制代码

# waveform 的前5个元素（通道维度为1，所以取 [0] 查看）
print(waveform[0, :5])  
# 输出：tensor([0.0000, 0.0859, 0.1696, 0.2466, 0.3183], dtype=torch.float32)

频谱图

如果把声音比作 "一道彩虹"，那频谱图就是 "拆解彩虹的工具"------ 它能让你看清：这道声音里藏了哪些 "颜色"（频率），每种 "颜色" 在不同时间有多 "亮"（强度）。

先从 "声音的本质" 说起

声音是空气的振动，就像你摇绳子时产生的波浪：

有的振动 "快"（比如蚊子嗡嗡叫）→ 我们听着 "音调高"，这叫 "高频"；
有的振动 "慢"（比如大鼓咚咚响）→ 我们听着 "音调低"，这叫 "低频"；
有的振动 "幅度大"（比如大喊）→ 我们听着 "声音响"，这叫 "强度高"；
有的振动 "幅度小"（比如耳语）→ 我们听着 "声音轻"，这叫 "强度低"。

但问题是：普通的声音（比如唱歌、说话）不是 "单一振动"，而是 "很多不同频率的振动混在一起"------ 就像彩虹是 "很多颜色混在一起" 一样。你直接听声音，只能知道 "好不好听"，却不知道里面有哪些 "高频 / 低频"，以及这些频率什么时候强、什么时候弱。

频谱图：把 "混合声音" 拆成 "时间 + 频率 + 强度" 的图

频谱图就是用 "一张二维图"，把这些藏在声音里的细节直观地画出来，三个核心维度一看就懂：

图的维度	对应声音的什么属性？	举个例子（听一首歌）
横轴（左右）	时间（从左到右是声音的播放顺序）	左边是歌曲开头，右边是歌曲结尾
纵轴（上下）	频率（从下到上是音调从低到高）	下面是贝斯的低频，上面是高音的高频
颜色深浅	强度（颜色越亮 / 越深，声音越响）	歌手唱歌时颜色变亮，伴奏弱时颜色变暗

用 "唱歌" 的例子看懂频谱图

假设你唱一句 "哆（1）- 来（2）- 咪（3）"：

唱 "哆"（低频）时：频谱图的 "下方区域"（低频区）会出现一块亮斑，而且在 "唱哆的时间段"（横轴某一段）内持续亮；
唱 "来"（中高频）时：亮斑会 "往上移" 到 "中间区域"（中高频区），对应 "来的时间段"；
唱 "咪"（更高频）时：亮斑会继续 "往上移" 到 "上方区域"（高频区），对应 "咪的时间段"；
如果你唱 "哆" 时声音比 "咪" 大："哆" 对应的亮斑会比 "咪" 的亮斑更亮。

这样一来，哪怕你没听过这句歌，只要看频谱图，也能知道：什么时候唱了什么音调、哪个音调更响 ------ 这就是频谱图的核心作用：把 "看不见的声音细节" 变成 "看得见的图"。

理想纯 440Hz 正弦波的核心特性是：频率单一且不随时间变化 ------ 从信号开始到结束，每个时间点的频率成分只有 440Hz，没有任何其他频率（如谐波、噪音）。

在语谱图中：

纵轴（频率）：440Hz 是固定位置，不会上下偏移；
横轴（时间）：每个时间点的频率都是 440Hz，因此所有时间点在 440Hz 处的 "能量" 都会被标注（颜色高亮）；
颜色：由于纯音的能量稳定（若幅度不变），这条直线的颜色深浅会保持一致（不会忽明忽暗）。

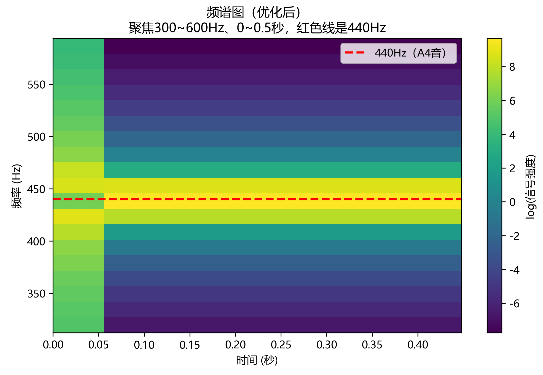
语谱图右侧的 "颜色刻度"（专业上叫颜色映射条 / 强度标尺），本质是 "颜色深度与能量（或幅度）的对应关系说明书"，而不是直接代表某个固定能量值。最终判断能量强弱，核心看颜色深度，但这个 "深度" 的具体物理意义，需要结合右侧刻度来解读。

先看懂刻度："log (信号强度)" 的本质是 "压缩动态范围"

上图右侧刻度是 log(信号强度) ，不是 "信号强度" 本身。核心逻辑：

对数转换的作用 ：电子化声音（比如合成器、音频软件生成的纯音）的 "信号强度动态范围极大"（强能量和弱能量差距可能达到 10⁶倍以上）。直接用 "线性刻度" 展示，弱能量会被 "挤成白色"，看不到细节；用 log() 转换后，能把大范围的能量差异压缩到小范围，让强弱能量都能显示（类似相机的 HDR 模式，亮部和暗部都能看清）。
刻度 "0" 的意义 ：log(信号强度)=0 对应 "信号强度 = 1"（因为 log(1)=0 ），但这里的 "1" 是 "归一化后的相对值" （不是实际物理能量的绝对值）。也就是说：
- 颜色越深（接近黄色）→ log(信号强度) 越大 → 实际信号强度越强；
- 颜色越浅（接近紫色）→ log(信号强度) 越小 → 实际信号强度越弱。

也就是归一化 1就是最大的，log(1)=0 也就是说0的时候颜色是最深的。

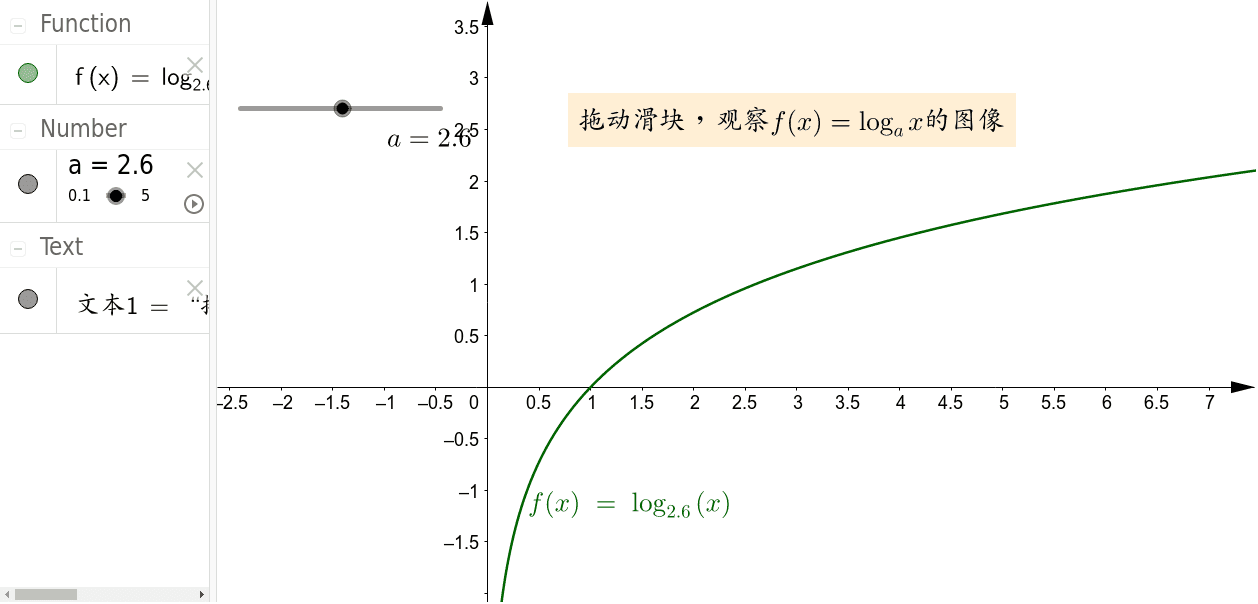
上图只是看下log函数的特点，没其他计算用途。

代码

复制代码

# --------------------------
# 3.2 频谱图（优化后：聚焦440Hz，放大细节，添加标记）
# --------------------------
n_fft = 1024  # 傅里叶变换窗口大小（不变）
spectrogram_transform = T.Spectrogram(n_fft=n_fft)
spectrogram = spectrogram_transform(waveform)  # (1, 513, 63) → (通道, 频率点, 时间帧)

# 1. 计算实际频率轴和时间轴（不变，但后续会用）
freq_axis = torch.fft.rfftfreq(n_fft, 1/sample_rate).numpy()  # 0 ~ 8000Hz
time_axis = np.arange(spectrogram.shape[2]) * (n_fft / sample_rate)  # 0 ~ 2秒

# 2. 关键优化：聚焦440Hz附近的频率范围（砍掉无关频率）
focus_freq_min = 300  # 只显示300Hz以上
focus_freq_max = 600  # 只显示600Hz以下
# 找到300~600Hz在freq_axis中的索引（用于截取频谱图）
freq_mask = (freq_axis >= focus_freq_min) & (freq_axis <= focus_freq_max)
focused_spectrogram = spectrogram[0, freq_mask, :]  # 截取300~600Hz的频谱
focused_freq_axis = freq_axis[freq_mask]  # 截取对应的频率轴

# 3. 关键优化：聚焦前0.5秒的时间范围（砍掉无关时间，让亮斑更粗）
focus_time_min = 0    # 从0秒开始
focus_time_max = 0.5  # 只显示前0.5秒
time_mask = (time_axis >= focus_time_min) & (time_axis <= focus_time_max)
focused_spectrogram = focused_spectrogram[:, time_mask]  # 截取0~0.5秒的频谱
focused_time_axis = time_axis[time_mask]  # 截取对应的时间轴

# 4. 绘制优化后的频谱图
im1 = axes[0,1].imshow(
    torch.log(focused_spectrogram + 1e-8),  # log增强对比度
    cmap='viridis', 
    aspect='auto',  # 自动调整宽高比，避免拉伸
    origin='lower',
    # 绑定实际坐标（重点：让轴显示300~600Hz、0~0.5秒，而非索引）
    extent=[focused_time_axis[0], focused_time_axis[-1], 
            focused_freq_axis[0], focused_freq_axis[-1]]
)

# 5. 关键优化：添加440Hz参考线（一眼找到目标频率）
axes[0,1].axhline(y=440, color='red', linestyle='--', linewidth=2, label='440Hz（A4音）')
axes[0,1].legend()  # 显示图例

# 其他优化：标签和标题更明确
axes[0,1].set_title('频谱图（优化后）\n聚焦300~600Hz、0~0.5秒，红色线是440Hz', fontsize=12)
axes[0,1].set_xlabel('时间 (秒)', fontsize=10)
axes[0,1].set_ylabel('频率 (Hz)', fontsize=10)
plt.colorbar(im1, ax=axes[0,1], label='log(信号强度)')  # 颜色条说明强度含义

输出：

一、先明确：这段代码的目标

我们已经有了一个 "2 秒长、440Hz 的纯音波形"（waveform），现在要把它转换成 "频谱图"，并通过优化让图中 "440Hz 的信号" 一眼就能看到。

二、逐部分详解代码

基础参数与频谱图生成

python 复制代码

n_fft = 1024  # 傅里叶变换窗口大小（不变）
spectrogram_transform = T.Spectrogram(n_fft=n_fft)
spectrogram = spectrogram_transform(waveform)  # (1, 513, 63) → (通道, 频率点, 时间帧)

n_fft = 1024：傅里叶变换的 "窗口大小"（一次分析 1024 个采样点）。窗口越大，频率分析越精确，但时间分析越粗糙（权衡关系）。
T.Spectrogram(n_fft=n_fft) ：用torchaudio的工具创建一个 "频谱图转换器"，本质是对音频做 "短时傅里叶变换"（STFT）。
spectrogram = ... ：将波形waveform转换为频谱图。输出形状(1, 513, 63)的含义：
- 1：音频通道数（单声道）；
- 513：频率点数量（对应 0~8000Hz 的频率范围）；
- 63：时间帧数量（2 秒音频被分成 63 个小窗口，每个窗口约 32 毫秒）。

假设 spectrogram 是一个形状为 (1, 513, 63) 的数组，可拆解为：

第 1 个维度（通道） ：[0]（单声道，只有 1 个通道）；
第 2 个维度（频率） ：[0]~[512]（513 个频率点，对应 0~8000Hz）；
第 3 个维度（时间） ：[0]~[62]（63 个时间帧，对应 0~2 秒）。

其数据结构类似下图（只展示部分关键位置，省略中间值）：

python 复制代码

spectrogram = [
    [  # 第0通道（唯一通道）
        [10, 12, 15, ..., 8],   # 第0频率点（0Hz）：63个时间帧的能量
        [5, 7, 9, ..., 6],     # 第1频率点（≈31.25Hz）：63个时间帧的能量
        ...,
        [200, 210, 205, ..., 190],  # 第x频率点（440Hz）：63个时间帧的能量
        ...,
        [3, 2, 4, ..., 1]      # 第512频率点（8000Hz）：63个时间帧的能量
    ]
]

2. 计算实际的 "频率轴" 和 "时间轴"

python 复制代码

# 1. 计算实际频率轴和时间轴（不变，但后续会用）
freq_axis = torch.fft.rfftfreq(n_fft, 1/sample_rate).numpy()  # 0 ~ 8000Hz
time_axis = np.arange(spectrogram.shape[2]) * (n_fft / sample_rate)  # 0 ~ 2秒

freq_axis ：生成 "实际频率值" 的数组（单位 Hz）。
因为n_fft=1024、采样率 16000Hz，所以频率范围是0 ~ 8000Hz（采样率的一半，奈奎斯特极限），共 513 个点（1024/2 + 1）。
time_axis ：生成 "实际时间值" 的数组（单位秒）。
每个时间帧的长度 = n_fft / 采样率 = 1024/16000 ≈ 0.064秒，63 个帧总时长≈2 秒，和原始音频一致。

3. 优化 1：聚焦 440Hz 附近的频率（砍掉无关频率）

python 复制代码

# 2. 关键优化：聚焦440Hz附近的频率范围（砍掉无关频率）
focus_freq_min = 300  # 只显示300Hz以上
focus_freq_max = 600  # 只显示600Hz以下
# 找到300~600Hz在freq_axis中的索引（用于截取频谱图）
freq_mask = (freq_axis >= focus_freq_min) & (freq_axis <= focus_freq_max)
focused_spectrogram = spectrogram[0, freq_mask, :]  # 截取300~600Hz的频谱
focused_freq_axis = freq_axis[freq_mask]  # 截取对应的频率轴

为什么要聚焦？：原始频谱图显示 0~8000Hz，440Hz 只占很小一块，信号容易被稀释。
freq_mask ：生成一个 "布尔数组"，标记freq_axis中哪些频率在 300~600Hz 范围内（True表示保留，False表示丢弃）。
focused_spectrogram ：用freq_mask截取频谱图，只保留 300~600Hz 的频率部分（刚好包含 440Hz），其他高频 / 低频全砍掉。

4. 优化 2：聚焦前 0.5 秒的时间（砍掉无关时间）

python 复制代码

# 3. 关键优化：聚焦前0.5秒的时间范围（砍掉无关时间，让亮斑更粗）
focus_time_min = 0    # 从0秒开始
focus_time_max = 0.5  # 只显示前0.5秒
time_mask = (time_axis >= focus_time_min) & (time_axis <= focus_time_max)
focused_spectrogram = focused_spectrogram[:, time_mask]  # 截取0~0.5秒的频谱
focused_time_axis = time_axis[time_mask]  # 截取对应的时间轴

为什么要聚焦？：原始频谱图显示 2 秒的全时间，440Hz 的信号是一条 "细长的亮线"，不显眼。截取前 0.5 秒后，亮线变 "粗"，视觉上更突出。
time_mask ：标记time_axis中哪些时间在 0~0.5 秒范围内。
focused_spectrogram：进一步截取时间维度，只保留前 0.5 秒的频谱，让信号更集中。

5. 绘制优化后的频谱图（核心可视化）

python 复制代码

# 4. 绘制优化后的频谱图
im1 = axes[0,1].imshow(
    torch.log(focused_spectrogram + 1e-8),  # log增强对比度
    cmap='viridis', 
    aspect='auto',  # 自动调整宽高比，避免拉伸
    origin='lower',
    # 绑定实际坐标（重点：让轴显示300~600Hz、0~0.5秒，而非索引）
    extent=[focused_time_axis[0], focused_time_axis[-1], 
            focused_freq_axis[0], focused_freq_axis[-1]]
)

torch.log(focused_spectrogram + 1e-8) ：对频谱值取对数（+1e-8避免 log (0) 报错）。
作用：增强弱信号的对比度 ------ 原始频谱中 440Hz 的信号强度远高于其他频率，取 log 后明暗差异更明显。
cmap='viridis'：设置颜色映射（用绿色 - 黄色 - 紫色表示强度从低到高）。
origin='lower'：让频率轴 "从下到上递增"（符合直觉：下面是低频，上面是高频）。
extent：绑定坐标轴的实际数值（x 轴 0~0.5 秒，y 轴 300~600Hz），避免显示抽象的 "索引值"。

6. 添加参考线和标签（让图 "能看懂"）

python 复制代码

# 5. 关键优化：添加440Hz参考线
axes[0,1].axhline(y=440, color='red', linestyle='--', linewidth=2, label='440Hz（A4音）')
axes[0,1].legend()  # 显示图例

# 其他优化：标签和标题
axes[0,1].set_title('频谱图（优化后）\n聚焦300~600Hz、0~0.5秒，红色线是440Hz', fontsize=12)
axes[0,1].set_xlabel('时间 (秒)', fontsize=10)
axes[0,1].set_ylabel('频率 (Hz)', fontsize=10)
plt.colorbar(im1, ax=axes[0,1], label='log(信号强度)')  # 颜色条说明强度含义

axhline(y=440)：在 440Hz 的位置画一条红色虚线，直接标记目标频率，一眼就能找到信号位置。
颜色条：说明 "颜色深浅" 对应 "信号强度"（log 值越大，颜色越亮，信号越强）。
标题和标签：明确图的内容（聚焦范围、参考线含义），避免歧义。

梅尔频谱图

梅尔频谱图（Mel Spectrogram）是基于人耳听觉特性优化的频谱图，核心是将传统频谱图的 "线性频率轴" 转换为 "符合人耳感知的梅尔频率轴"，让频谱更贴近人类对声音的主观感受。它是语音识别、音乐分析等领域的核心特征，比传统频谱图更能捕捉声音的关键信息。

一、先理解核心：人耳的 "非线性听觉特性"

传统频谱图用 "线性频率轴"（如 0~8000Hz 均匀分布），但人耳对频率的感知并非线性 ------对低频声音的频率差异更敏感，对高频声音的频率差异更迟钝。

举个例子：

人耳能轻松区分 200Hz 和 300Hz（差异 100Hz）的声音；
但很难区分 7000Hz 和 7100Hz（同样差异 100Hz）的声音，甚至需要差异 500Hz 以上才能感知到。

这种特性可用 "梅尔刻度（Mel Scale）" 量化：1 梅尔（Mel）对应人耳感知到的 "1000Hz 纯音的音高变化单位" ，频率与梅尔的换算关系为：

Mel(f)=2595×log10(1+700f)

f：实际频率（Hz）；
当 f=1000Hz 时，Mel(1000)=1000，即 1000Hz 对应 1000 梅尔；
频率越高，梅尔值增长越慢（体现人耳对高频的迟钝）。

二、梅尔频谱图的本质："传统频谱图 + 梅尔滤波"

梅尔频谱图不是直接对波形计算，而是在传统短时傅里叶变换（STFT）频谱图的基础上，通过 "梅尔滤波器组" 处理得到的，流程如下：

第一步：计算传统频谱图（同之前的步骤）

对音频波形分帧，每帧做 STFT，得到 "频率（Hz）- 时间 - 能量" 的三维频谱图（如之前的 (1, 513, 63) 结构），并对能量取平方得到 "功率谱（Power Spectrum）"。

第二步：设计 "梅尔滤波器组"

根据梅尔刻度，在 "线性频率轴" 上生成一组三角滤波器（通常 20~40 个），特点是：

低频区域：滤波器密度高（相邻滤波器重叠多），对应人耳对低频的敏感；
高频区域：滤波器密度低（相邻滤波器重叠少），对应人耳对高频的迟钝；
所有滤波器覆盖人耳可听范围（通常 20Hz~20000Hz），且总能量守恒（避免信息丢失）。

例：若设计 26 个梅尔滤波器，传统频谱图的 513 个频率点会被 "合并" 为 26 个梅尔频率点 ------ 每个梅尔频率点的能量，是该滤波器覆盖的所有线性频率点能量的加权和。

第三步：生成梅尔频谱图

将传统功率谱通过 "梅尔滤波器组"，得到 "梅尔频率 - 时间 - 能量" 的三维数组，这就是梅尔频谱图。

形状示例：若输入是单声道、63 个时间帧、26 个梅尔滤波器，梅尔频谱图的形状为 (1, 26, 63)（通道数 × 梅尔频率数 × 时间帧数）；
视觉上：低频区域的 "频率分辨率" 高，高频区域的 "频率分辨率" 低，更贴近人眼对声音感知的直觉。

第四步：（可选）取对数增强细节

与传统频谱图类似，通常会对梅尔频谱的能量取对数（log(Mel Spectrum + 1e-8)），目的是：

压缩能量的动态范围（让弱能量的细节更清晰，如语音中的辅音）；
更符合人耳对 "音量" 的对数感知特性（人耳对音量的感知与能量的对数成正比）。

三、梅尔频谱图 vs 传统频谱图：核心差异

通过表格直观对比两者的关键区别：

对比维度	传统频谱图（Linear Spectrogram）	梅尔频谱图（Mel Spectrogram）
频率轴	线性频率（Hz），均匀分布	梅尔频率（Mel），低频密集、高频稀疏
听觉匹配度	不匹配人耳特性（高频分辨率过剩，低频不足）	高度匹配人耳特性，更贴近主观听感
维度（频率点）	多（如 n_fft=1024 时为 513 个）	少（通常 20~40 个梅尔滤波器）
数据冗余度	高（高频区域信息冗余，人耳无法感知）	低（去除冗余，保留关键感知信息）
核心应用场景	通用频率分析（如纯音检测、噪音分析）	语音识别（ASR）、音乐分类、情感识别等

代码

复制代码

# --------------------------
# 3.3 梅尔频谱图（优化：同样绑定实际时间/梅尔频率）
# --------------------------
mel_transform = T.MelSpectrogram(
    sample_rate=sample_rate,
    n_fft=n_fft,
    n_mels=64,
    f_max=8000  # 最大频率8000Hz（与采样率匹配）
)
mel_spectrogram = mel_transform(waveform)  # (1, 64, 63) → (通道数, 梅尔频带, 时间帧)

# 绘制梅尔频谱图
im2 = axes[1,0].imshow(
    torch.log(mel_spectrogram[0] + 1e-8),
    cmap='viridis',
    aspect='auto',
    origin='lower',
    extent=[time_axis[0], time_axis[-1], 0, 64]  # 梅尔频带0~64（对应0~8000Hz）
)
axes[1,0].set_title('梅尔频谱图\n（人耳敏感的频率范围）', fontsize=12)
axes[1,0].set_xlabel('时间 (秒)', fontsize=10)
axes[1,0].set_ylabel('梅尔频带', fontsize=10)
plt.colorbar(im2, ax=axes[1,0], label='log(强度)')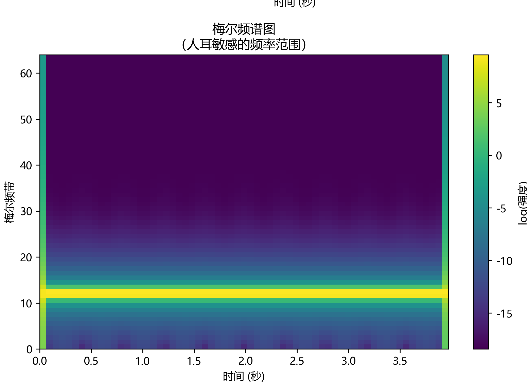

可通过以下代码验证 440Hz 对应的能量分布：

复制代码

import torch
import librosa.display
import matplotlib.pyplot as plt

# 假设 mel_spectrogram 是 (1, 64, 63) 的张量
mel_bands = mel_spectrogram[0].numpy()  # 提取单通道梅尔频谱

# 找到能量最高的频带索引
max_band = mel_bands.argmax(axis=0)  # 每一时间帧的最高能量频带
print("平均最高频带索引：", max_band.mean())  # 看是否接近14

若输出接近 14，说明理论计算与实际一致，黄色亮带的 "10-20 范围" 是滤波器重叠的正常现象。

假设 mel_spectrogram 是 PyTorch 张量，形状为 (1, 64, 63)，对应：

第 1 维（通道数） ：1 → 单声道音频（若为立体声则为 2）；
第 2 维（梅尔频带） ：64 → 64 个梅尔滤波器（对应 0~8000Hz 的非线性映射）；
第 3 维（时间帧） ：63 → 63 个时间窗口（覆盖音频总时长，如 2 秒）。

数据结构示意图（简化版，仅展示关键位置）：

python 复制代码

mel_spectrogram = torch.tensor([
    [  # 第0通道（单声道）
        [0.02, 0.03, 0.02, ..., 0.01],  # 第0梅尔频带（最低频，≈20Hz）：63帧能量
        [0.05, 0.06, 0.05, ..., 0.04],  # 第1梅尔频带：63帧能量
        ...,
        [2.1, 2.3, 2.2, ..., 2.0],      # 第14梅尔频带（≈440Hz）：63帧能量（高能量）
        ...,
        [0.01, 0.01, 0.02, ..., 0.01],  # 第63梅尔频带（最高频，≈8000Hz）：63帧能量
    ]
])

MFCC特征图

MFCC（Mel - Frequency Cepstral Coefficients，梅尔频率倒谱系数）特征图是音频信号处理与语音识别领域里，对音频特征进行可视化呈现的一种方式，用于直观展示音频在不同时间、不同梅尔频率倒谱系数维度上的特征分布。下面从生成逻辑、构成要素、作用等方面详细介绍：

一、生成流程与原理

前期基础处理：先对音频做预处理（如读取音频、获取采样率），再通过短时傅里叶变换（STFT）将时域音频转为频域频谱，接着用梅尔滤波器组（模拟人耳听觉特性，对高频分辨率低、低频分辨率高）处理，得到梅尔频谱，之后经对数运算、离散余弦变换（DCT），最终提取出 MFCC 系数，这些系数构成 MFCC 特征图的数据基础。
核心逻辑：模拟人耳对声音的感知，突出与语音识别、音频分析相关的关键特征，压缩无关冗余信息，让特征更紧凑、更具区分度。

二、特征图的构成与解读

维度与坐标 ：
- 一般为二维热力图形式，横轴通常是时间帧索引 ，代表音频不同时刻；纵轴是 MFCC 系数索引（比如提取 13 个 MFCC 系数，纵轴就是 0 - 12 ），每个系数反映音频在特定 "倒谱特征维度" 上的信息，不同系数关注音频不同方面特征（如低频包络、高频细节等）。
- 颜色深浅对应特征值大小（颜色条标注数值含义，常与能量、系数强度相关），颜色深表示该时间帧下对应 MFCC 系数的强度或权重高。
示例解读：以一段语音的 MFCC 特征图为例，若某段时间（横轴某区间）、某几个 MFCC 系数（纵轴某区间）颜色较深，说明这段语音在对应时间里，这些倒谱维度特征更突出，可能和语音的音调、语速、音色等属性相关，比如低频相关系数（如前几个系数）颜色深，可能对应语音中低频能量丰富、声调平稳部分。

三、作用与应用场景

音频分析：帮助直观观察音频信号在时间和倒谱域的变化，识别音频中的关键特征（如语音的起始、结束，不同音素的切换），理解音频内容特性（如音乐的旋律走向、噪音干扰情况）。
语音识别：作为核心特征输入机器学习模型（如 LSTM、GRNN 等），特征图能辅助调试模型、分析特征有效性，比如看不同说话人、不同发音的 MFCC 特征图差异，优化特征提取与模型训练。
音乐信息检索：用于区分音乐风格、识别乐器音色，通过对比不同音乐片段的 MFCC 特征图，快速筛选出风格相似或包含特定乐器演奏的音频。

简单来说，MFCC 特征图是把音频复杂的特征信息，以直观可视化方式呈现，让我们能 "看见" 音频在梅尔频率倒谱域的特征变化，是音频信号处理、分析与建模的重要辅助工具。比如在语音识别研究里，可通过对比不同发音人的 MFCC 特征图，调整识别模型；在音频分类任务中，依据特征图差异设计分类规则。

代码

复制代码

# --------------------------
# 3.4 MFCC特征（优化：增加对比度，让系数差异更明显）
# --------------------------
mfcc_transform = T.MFCC(
    sample_rate=sample_rate,
    n_mfcc=13,
    melkwargs={'n_fft': n_fft, 'n_mels': 64, 'f_max': 8000}
)
mfcc = mfcc_transform(waveform)  # (1, 13, 63) → (通道数, MFCC系数, 时间帧)

# 绘制MFCC（优化：用vmin/vmax控制颜色范围，增强对比度）
im3 = axes[1,1].imshow(
    mfcc[0],
    cmap='viridis',
    aspect='auto',
    origin='lower',
    extent=[time_axis[0], time_axis[-1], 0, 12],  # MFCC系数0~12
    vmin=mfcc[0].min(),  # 颜色最小值=MFCC最小值
    vmax=mfcc[0].max()   # 颜色最大值=MFCC最大值
)
axes[1,1].set_title('MFCC特征\n（13个关键系数，音频"指纹"）', fontsize=12)
axes[1,1].set_xlabel('时间 (秒)', fontsize=10)
axes[1,1].set_ylabel('MFCC系数', fontsize=10)
plt.colorbar(im3, ax=axes[1,1], label='系数值')

# 调整子图间距，避免标签重叠
plt.tight_layout()
# 保存图像（dpi=300确保高清，bbox_inches='tight'避免标签被截断）
plt.savefig('audio_features_visualization_optimized.png', dpi=300, bbox_inches='tight')
plt.show()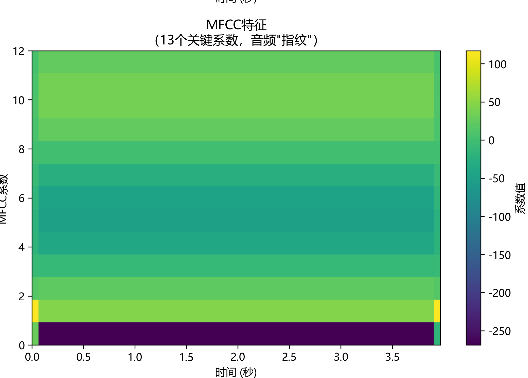

1.T.MFCC`参数解析（特征提取的 "规则设定"）

python 复制代码

mfcc_transform = T.MFCC(
    sample_rate=sample_rate,  # 采样率（16000Hz，与音频一致）
    n_mfcc=13,  # 提取13个MFCC系数（语音识别的标准配置）
    melkwargs={'n_fft': n_fft, 'n_mels': 64, 'f_max': 8000}  # 梅尔频谱的参数
)

sample_rate：必须与输入音频的采样率一致（这里是 16000Hz），确保频率计算准确。
n_mfcc=13 ：指定提取 13 个 MFCC 系数。
- 为什么是 13 个？前 13 个系数包含了音频最关键的声学特征（低阶系数反映整体轮廓，高阶阶系数反映细节），更多系数会引入冗余，更少则则丢失信息。
melkwargs ：传递给梅尔频谱的参数（MFCC 基于梅尔频谱计算，因此需要先定义梅尔频谱的参数）：
- n_fft：傅里叶变换窗口大小（之前定义为 1024，控制频率分辨率）；
- n_mels=64：梅尔滤波器数量（64 个频带，覆盖 0~8000Hz）；
- f_max=8000：最高频率（与采样率 16000Hz 匹配，因奈奎斯特频率为 8000Hz）。

2. 提取 MFCC 特征：mfcc = mfcc_transform(waveform)

输入：waveform是原始音频波形（形状通常为(1, N)，1 是单声道，N 是总采样点数）。
输出：mfcc是 MFCC 特征张量，形状为(1, 13, 63)，各维度含义：
- 第 1 维（1）：通道数（单声道）；
- 第 2 维（13）：13 个 MFCC 系数（索引 0~12）；
- 第 3 维（63）：时间帧数量（与之前的梅尔频谱一致，每帧对应约 0.03 秒）。
计算逻辑 ：MFCC 提取是 "梅尔频谱→对数转换→DCT 变换" 的三步过程：
1. 先计算梅尔频谱（用melkwargs参数）；
2. 对梅尔频谱取对数（增强低能量细节）；
3. 做离散余弦变换（DCT），取前 13 个系数（过滤高频冗余，保留关键特征）。