前缀和数组的介绍:
前缀和数组是一种重要的数据结构,它能够高效地解决一系列与区间求和相关的问题。在处理一维或多维数组时,前缀和数组可以快速计算任意区间内元素的总和,这在算法设计中尤为重要。
前缀和数组的定义:
- 前缀和数组是基于原始数组构建的,
- 其每个元素存储了从数组开始到当前索引位置的元素累加和。
简单来说就是:数组节点存储开始节点到本节点数据的和
一维数组前缀和:
- 一维前缀和的核心思想是构建一个前缀和数组 s,
- 其中 s[i] 表示从数组起点到第 i 个元素的累加和。
- 前缀和数组构建公式为: s[0]=a[1] (先保存第一个数据) s[i] = s[i-1] + a[i]
- 区间和 = s[r] - s[l-1] (需要注意的是要防止越界)
- 空间复杂度 O(N) 需要消耗一定的空间
- 时间复杂度 O(1) 常量的时间复杂度
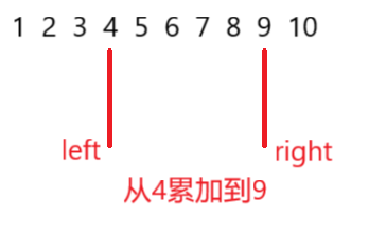
两个位置区间的和:
使用循环的方式从起点遍历到终点进行累加
cpp
int number_sum(int arr[],int left,int right){
int sum=0;
for(int i=left;i<=right;i++){
sum+=arr[i];
}
return sum;
} 前缀和数组的构建:
- 首先构建前缀和数组 创建一个数组
- 由于第一个数据前面没有数据,所以直接放入到前缀和数组中
- 第二个数据开始,每次添加之前的前缀和 s[i]=s[i-1]+a[i]
cpp
#include<iostream>
using namespace std;
int a[10]={1,2,3,4,5,6,7,8,9,10};
int s[10];//创建前缀和数组
int main(){
//把第一个数组存入
s[0]=a[0];
//从第二个数据开始按照公式存入
for(int i=1;i<10;i++){
s[i]=s[i-1]+a[i];
}
return 0;
} 
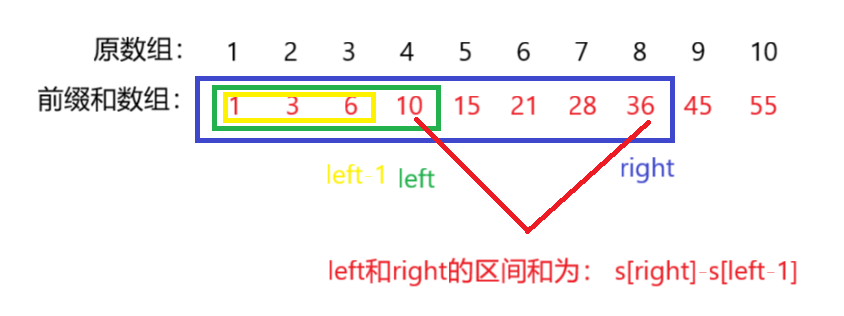
获取一个区间的和:
假设我们要求 left ~right 区间范围内的和
- s[left] 存储了 0~left的和
- s[right] 存储了 0~right的和
- 要求left~right的区间和
- 只需要让s[right]- s[left-1] == left-right 这个区间的和
cpp
int get_sum(int s[],int left,int right){
return s[right]-s[left-1];
}
需要注意的是:
- 当left 为数组第一个位置时 left-1会数组越界
- 解决方法1:对left进行判断处理 当left==第一个位置时 直接返回 s[right]
- 解决方法2:构建前缀和从下标1开始构建,下标0这个位置存储0 这样就可以完美解决。
cpp
int get_sum(int s[],int left,int right){
if(left==0) return s[right];//left为起点特殊处理
return s[right]-s[left-1];
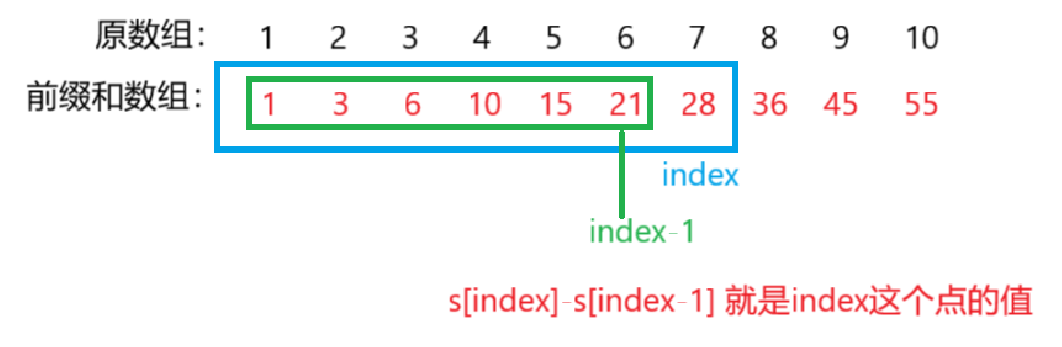
} 获取某个位置的值:
也可以使用前缀和去获取某个位置的值: index
- s[index] 代表的是 起点到index的和
- s[index-1]代表的是 起点到 index-1的和
- s[index] - s[index-1] 就是这个位置的值
- 需要注意的是 index==起点时,需要进行特殊处理
cpp
int get_data(int s[],int index){
if(index==0) return s[index];
return s[index]-s[index-1];
} 
求区间和:
题目分析:
题目的意思是:给出一个一维数组,然后给出多个区间,求每个区间的和
- 使用一维数组前缀和进行处理
相应程序:
cpp
#include<iostream>
using namespace std;
int a[100005];//存放数据 数组从1开始计数
int s[100005];//创建前缀和数组
int n,m;
int get_sum(int left,int right){
if(right==0) return s[right];
return s[right]-s[left-1];
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
s[i]=s[i-1]+a[i]; //由于下标从1开始,所以可以直接加上去即可
}
cin>>m;
int p,p1;
for(int i=1;i<=m;i++){
cin>>p>>p1;
cout<<get_sum(p,p1)<<endl;
}
return 0;
} 二维数组前缀和:
二维数组前缀和是一种在二维矩阵上进行快速区域求和的技术,它是一维前缀和概念的扩展。在二维数组中,前缀和可以帮助我们快速计算任意子矩阵的元素和,这在处理图像处理或者某些区域查询问题时非常有用。
二维前缀和的构建:
- 构建时按照指定点位到起始点位置构成的矩形
- 第一个点的前缀和为二维数组的第1个数据
- 构建公式为: s[x][y]=s[x][y-1]+s[x-1][y]-s[x-1][y-1]+a[x][y]
以下面的数据为例:
假设我要统计S[3][1]这个点位的前缀和该怎么处理呢?

我们可以把数据分为几个部分
- 左边的一部分
- 上边的一部分
- 本身这个位置的数据
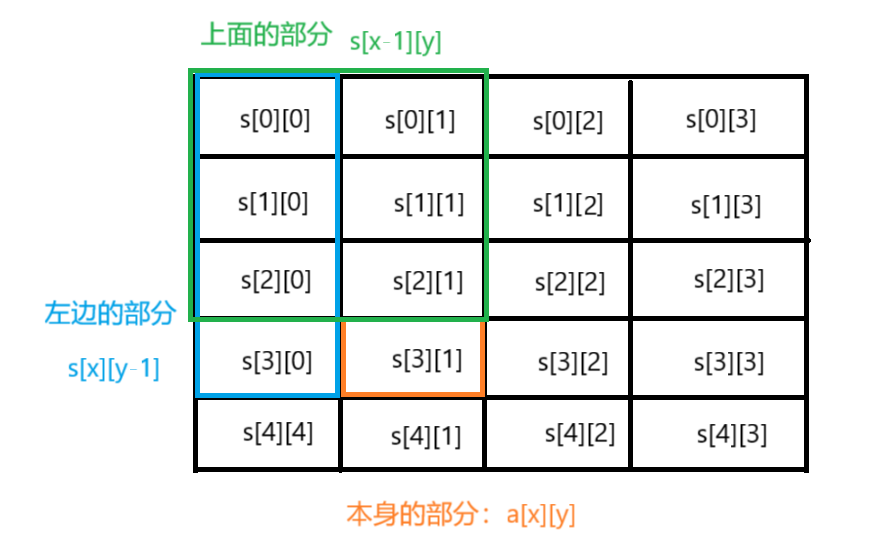
由于左边部分和右边部分重叠了一个区域,所以要减去这个区域
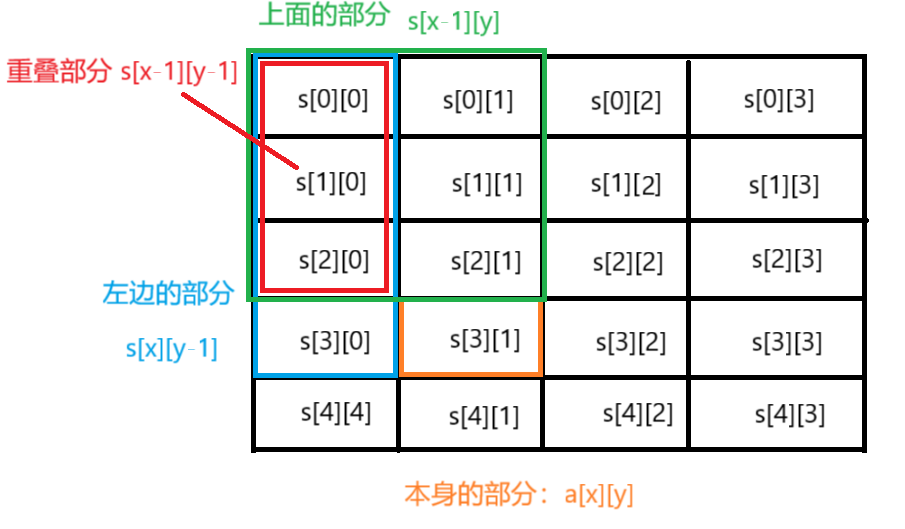
最后可以得到:s[x][y]=s[x][y-1]+s[x-1][y]-s[x-1][y-1]+a[x][y]
- 由于x和y都会减1
- 所以构建矩阵的时候最好从下标1开始构建,这样就不用判断数据的越界问题了
cpp
#include<iostream>
using namespace std;
int a[105][105];//存放数据 数组从下标1开始构建
int s[105][105];//创建前缀和数组
int n,m;//行数列数
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];//输入数据
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];//构建前缀和
}
}
return 0;
} 起点到位置区间和:
由于是从起点到指定位置(x,y)的区间和直接返回s[x][y]即可
cpp
int get_Sum(int x,int y){
return s[x][y];
} 某个区间的区间和:
起点:x1 y1 终点 x2 y2
结果为:s[x2][y2]-s[x1][y1]=s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]

需要注意的时:当我们用图形去模拟时,坐标会出现问题:需要将x1减去1 y1减去1
所以最后的式子为:s[x2][y2]-s[x1][y1]=s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]
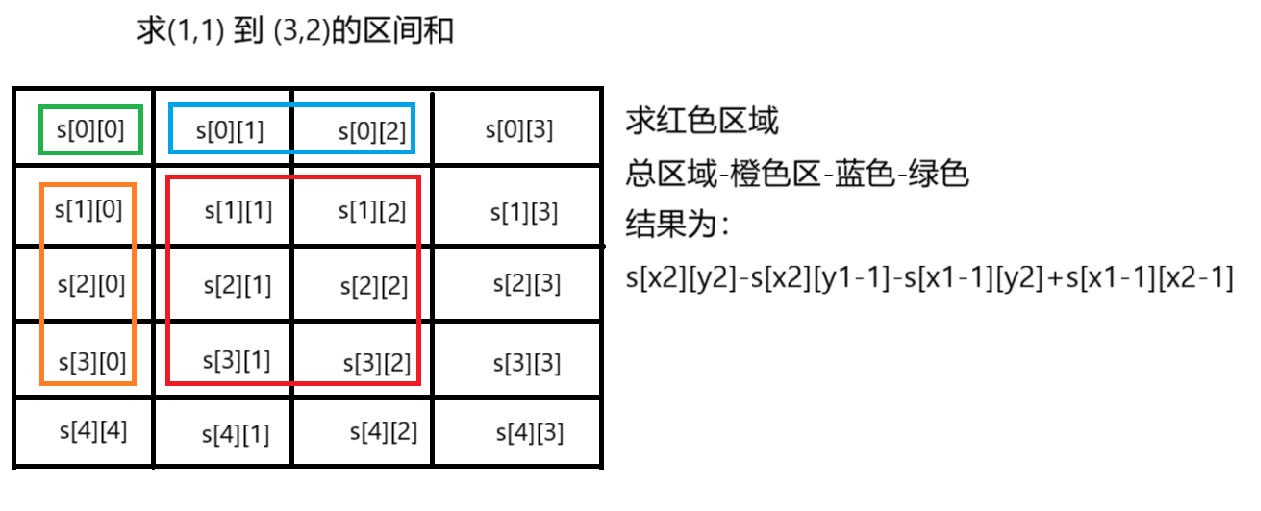
cpp
int get_Sums(int x1,int y1,int x2,int y2){
return s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1];
} 黑白格:
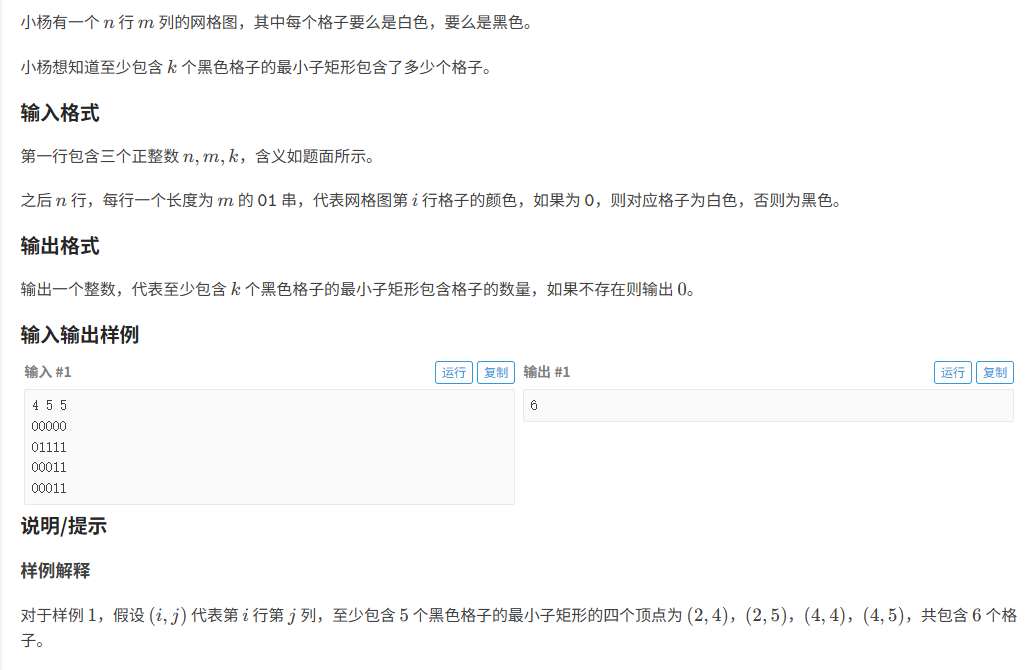

题目分析:
题目的意思是:给出一个只有0,1的矩阵,现在给出一个k代表1的个数
求这个二维数组中包含k个1的矩阵且占的格子最小,没有的话输出0。
- 需要求最小的矩阵且矩阵中有k个1
暴力求解(60/100):
- 我们枚举每一个矩阵中的所有矩形
- 判断矩形中是否容纳k个1
- 如果容纳了保存其矩阵所占的格子(x2-x1+1)*(y2-y1+1) 数组下标以1开始
- 保留最小的格子数
- 这种方法需要6个循环嵌套(时间复杂度高)
相应程序:
cpp
#include<iostream>
using namespace std;
char arr[103][103];//存放矩阵,从1-n 1-m
int number=0;//统计1的个数
int min1=5000000;//包含格子数
int n,m,k;
int main(){
cin>>n>>m>>k;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>arr[i][j];
if(arr[i][j]=='1') number++;
}
}
if(number<k) cout<<0<<endl;//不存在输出0
else{
for(int x1=1;x1<=n;x1++){ //起点的x坐标
for(int y1=1;y1<=m;y1++){ //起点的y坐标
for(int x2=x1;x2<=n;x2++){ //终点的x坐标
for(int y2=y1;y2<=m;y2++){//终点的y坐标
int num=(x2+1-x1)*(y2+1-y1);//区域方格的个数
if(num>=k){
int num1=0; //统计1的个数
for(int x=x1;x<=x2;x++){
for(int y=y1;y<=y2;y++){
if(arr[x][y]=='1') num1++;
}
}
if(num1>=k) min1=min(min1,num);
if(min1==k){ //最小为本身的话直接退出
cout<<min1;
return 0;
}
}
}
}
}
}
cout<<min1;
}
return 0;
} 二维数组前缀和:
- 提前计算出矩形所占1的个数(只有0,1就是求前缀和)
- 这样可以少去两个嵌套循环
- 但这个方法需要多创建一个数组,需要消耗内存(空间换时间)
相应程序:
cpp
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,m,k;
cin>>n>>m>>k;
char a;//由于数据没有空格隔开,需要使用char类型读取数据
int f[n+1][m+1]={};
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a;
if(a=='1') f[i][j]++;
//加上当前位置的数字
f[i][j]=f[i][j]+f[i-1][j]+f[i][j-1]-f[i-1][j-1];
//构造前缀和数组
}
}
int ans=INT_MAX;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
//枚举左上角
for(int w=i;w<=n;w++){
for(int l=j;l<=m;l++){
//枚举右下角
if(f[w][l]-f[i-1][l]-f[w][j-1]+f[i-1][j-1]>=k){
//如果黑格子足够,就判断子矩阵大小是否更小
ans=min(ans,(w-i+1)*(l-j+1));
}
}
}
}
}
if(ans==INT_MAX) cout<<0;
//更新过答案,就输出答案,否则输出0
else cout<<ans;
return 0;
}黑白方块:
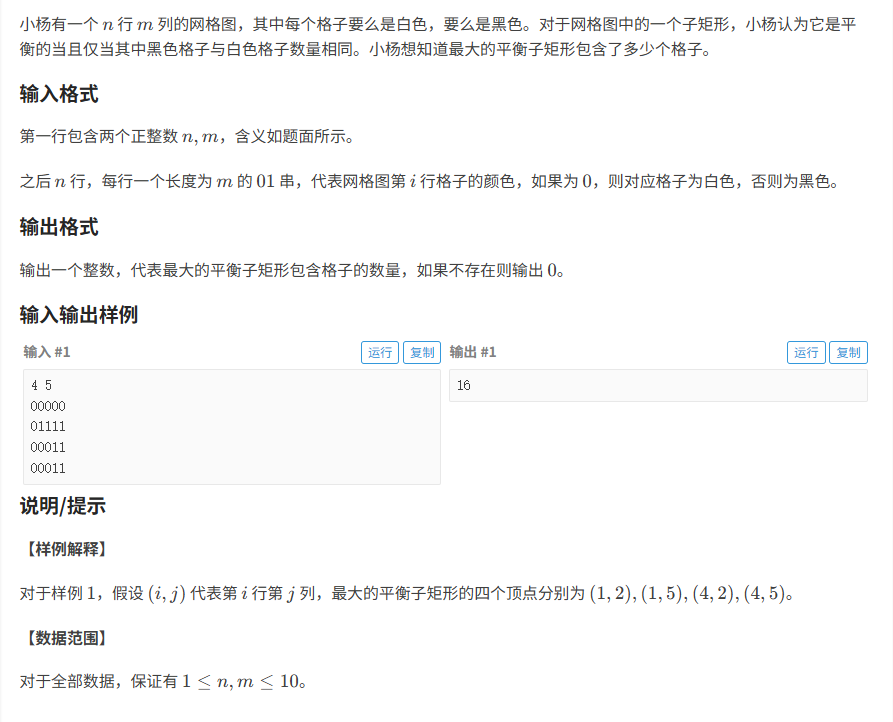
题目分析:
题目的意思:给你只有0 1的矩阵,求矩阵中0的个数和1的个数相同的矩阵(平衡矩阵)
- 求最大的平衡矩阵所占的格数
- 如果没有输出0
暴力求解:
- 枚举所有矩阵的情况
- 如果是平衡矩阵,保存其格子数
- 最后输出最大的那个格子数
相应程序:
cpp
#include<bits/stdc++.h>
using namespace std;
int n,m,ans,tmp;
char mp[20][20];
int cheak(int a,int b,int c,int d){
//a<=c b<=d
int cnt=0;
//枚举矩阵中的每个点
for(int i=a;i<=c;i++)
for(int j=b;j<=d;j++)
if(mp[i][j]=='1') cnt++;//统计黑格的个数
return 2*cnt==(c-a+1)*(d-b+1);//如果黑格子的数量为总数的一半,则为平衡矩阵
}
int main(){
cin>>n>>m;
//输入二维矩阵没有空格,一定要用char[][]
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>mp[i][j];
//不降原则枚举矩形的左上角(i,j)和右下角 (ii,jj)
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
for (int ii = i; ii <= n; ii++) {
for (int jj = j; jj <= m; jj++) {
if (cheak(i, j, ii, jj)){//cheak检查当前矩阵是否是平衡矩阵
//利用 (ii - i + 1) * (jj - j + 1)求出矩阵中点的总数
ans = max(ans, (ii - i + 1) * (jj - j + 1));
}
}
}
}
}
cout << ans << endl;
return 0;
}前缀和求解:
- 提前计算好每个矩阵的前缀和
- 枚举所有的矩阵
- 进行判断即可
相应程序:
cpp
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,m;
cin>>n>>m;
char a;//由于数据没有空格隔开,需要使用char类型读取数据
int f[n+1][m+1]={};
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a;
if(a=='1') f[i][j]++;
//加上当前位置的数字
f[i][j]=f[i][j]+f[i-1][j]+f[i][j-1]-f[i-1][j-1];
//构造前缀和数组
}
}
int ans=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
//枚举左上角
for(int w=i;w<=n;w++){
for(int l=j;l<=m;l++){
//枚举右下角
//计算格子的数量
int data=(w-i+1)*(l-j+1)
//判断是否为一半
if((f[w][l]-f[i-1][l]-f[w][j-1]+f[i-1][j-1])*2==data){
ans=max(ans,data);
}
}
}
}
}
cout<<ans;
return 0;
}