文章目录


题目描述
题目链接:394. 字符串解码
题目描述:
示例 1:
输入:s = "3[a]2[bc]"
输出:"aaabcbc"
示例 2:输入:s = "3[a2[c]]"
输出:"accaccacc"
示例 3:输入:s = "2[abc]3[cd]ef"
输出:"abcabccdcdcdef"
示例 4:输入:s = "abc3[cd]xyz"
输出:"abccdcdcdxyz"
提示:1 <= s.length <= 30
s 由小写英文字母、数字和方括号 '[]' 组成
s 保证是一个 有效 的输入。
s 中所有整数的取值范围为 [1, 300]
二、为什么这道题值得你花几分钟的时间弄懂?
这道题是栈结构应用的经典进阶题,更是面试中"考察逻辑思维与数据结构灵活运用"的高频题------它完美融合了"栈的嵌套处理"与"字符串操作"的核心逻辑,不仅考察我们对栈的理解,还考察对复杂字符串场景的拆解能力。
题目核心价值
- 栈能力的"试金石":集中考察
栈的入栈、出栈、嵌套匹配等核心用法,栈用得熟则解题如"简单题",反之则会将中等题变成困难题,是检验数据结构基础的绝佳案例。 - 直击嵌套问题核心:精准考察"嵌套结构处理"思维------如何将多层嵌套的
k[encoded_string]转化为栈可处理的顺序逻辑,是解题的核心,而非单纯的语法调用。 - 多知识点协同融合:串联"数字解析""字符串拼接"与"栈的状态管理",考察对不同知识点的搭配运用能力,而非单一知识点的机械记忆。
- 实际场景的"缩影":类似"嵌套解析"问题(如JSON解析、公式计算、模板渲染)在工作中高频出现,解题思路可直接迁移复用。
- 面试的"区分利器":能快速筛选出"只会死记语法"和"理解底层逻辑"的候选人------基础选手能靠栈的用法写出常规解法,进阶选手能优化字符串拼接效率、分析边界场景,契合面试选拔标准。
面试考察的核心方向
- 数据结构选型的底层逻辑:为何用栈而非其他结构,栈的"后进先出"特性如何匹配嵌套解析的场景,能否说清栈特性与题目场景的匹配度。
- 嵌套逻辑的拆解思维:能否快速想到"分层处理"核心思路,如何处理多层嵌套(如3[a2[c]]),能否清晰梳理每一步的栈状态变化。
- 语法与逻辑的协同:是否能将栈操作与"数字提取、字符串拼接"逻辑结合,避免"懂语法却想不出思路"或"有思路却写不对代码"。
- 复杂度分析的准确性:能否清晰说明栈解法的时间/空间代价,理解字符串拼接、栈操作对复杂度的影响。
- 边界场景的兼容能力:对多位数(如100[abc])、多层嵌套、纯字母字符串等特殊用例的处理,体现代码的稳健性。
掌握这道题,既能夯实栈结构的使用基础,又能加深理解"嵌套问题分层处理"的核心逻辑,后续遇到类似"嵌套解析"问题都能举一反三,无论笔试还是面试都能从容应对。
三、算法原理
本题核心算法是 "栈+分层解析",利用栈的"后进先出"特性处理嵌套结构,思路清晰且高效,步骤拆解如下:
如何解决问题?
字符串解码的核心难点是嵌套结构的处理(如3[a2[c]]),而栈的"后进先出"特性恰好能完美匹配这种"先遇到外层、后处理外层"的嵌套逻辑:
- 我们可以定义两个栈:
数字栈(numstack)存储重复次数k,字符串栈(strstack)存储待拼接的字符串; - 遍历字符串时,按字符类型分情况处理:
- 遇到数字:解析完整数字(处理多位数),压入数字栈;
- 遇到
[:解析后续的待重复字符串,压入字符串栈; - 遇到
]:弹出数字栈顶的重复次数、字符串栈顶的待重复字符串,将其重复后拼接到字符串栈的新栈顶; - 遇到字母:直接拼接到字符串栈的栈顶字符串中。
为了让整体的操作统一我们初始化的时候将字符串栈(strstack)先压入一个空字符串,用来将首位的字符串进行拼接(在模拟过程中步骤六可以体会)。
模拟过程
我们以覆盖单次数、多层嵌套、纯字母拼接、多位数重复 的案例 1[a2[bc]]de10[f] 为例,完整模拟每一步的栈状态变化,其中最后 10[f] 会重点体现多位数处理逻辑,循环拼接会省略。
初始状态
- 数字栈
numstack = [](存储重复次数) - 字符串栈
strstack = [""](初始空字符串,用于承接最外层拼接结果) - 索引
i = 0(遍历字符串的指针)
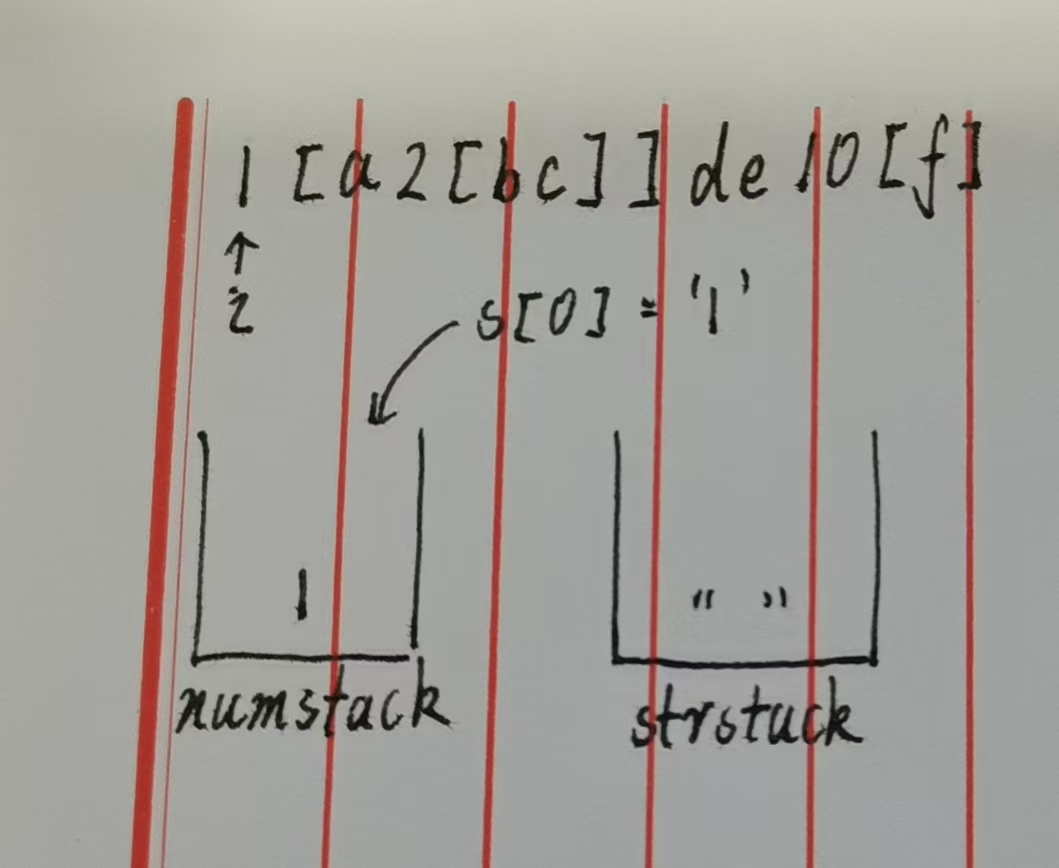
步骤1:解析数字 1(i=0)
- 字符
s[0] = '1',触发数字解析逻辑:- 解析完整数字:
an = 1,解析后i自增到1; - 将数字
1压入numstack→numstack = [1]。
- 解析完整数字:
此时栈状态如下图👇:
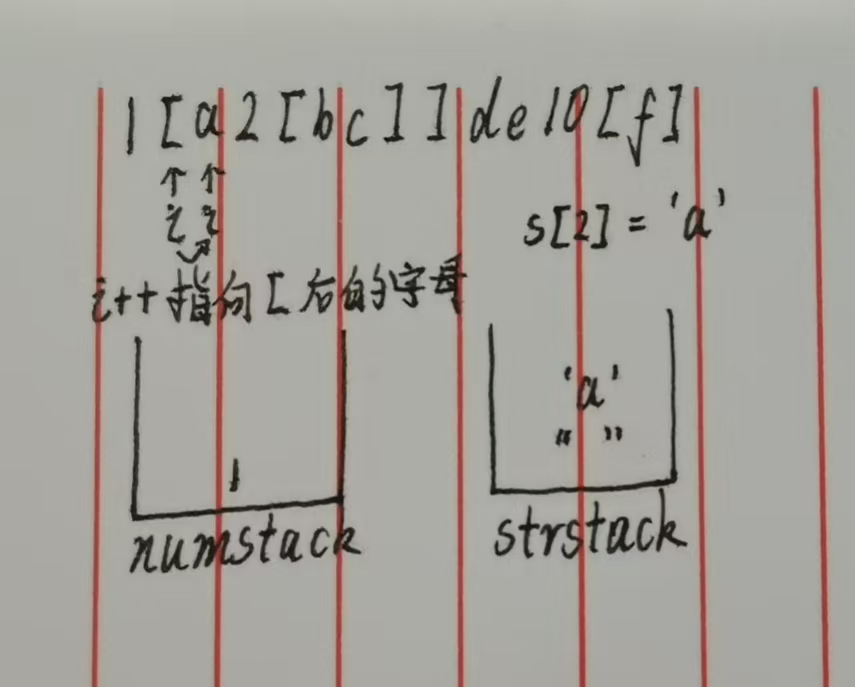
步骤2:解析左括号 [ 与字母 a(i=1)
- 字符
s[1] = '[',触发左括号逻辑:i自增到2,调用getStr解析字母:s[2] = 'a',得到字符串"a";- 将
"a"压入strstack→strstack = ["", "a"]; - 解析后
i自增到3。
此时栈状态如下图👇:
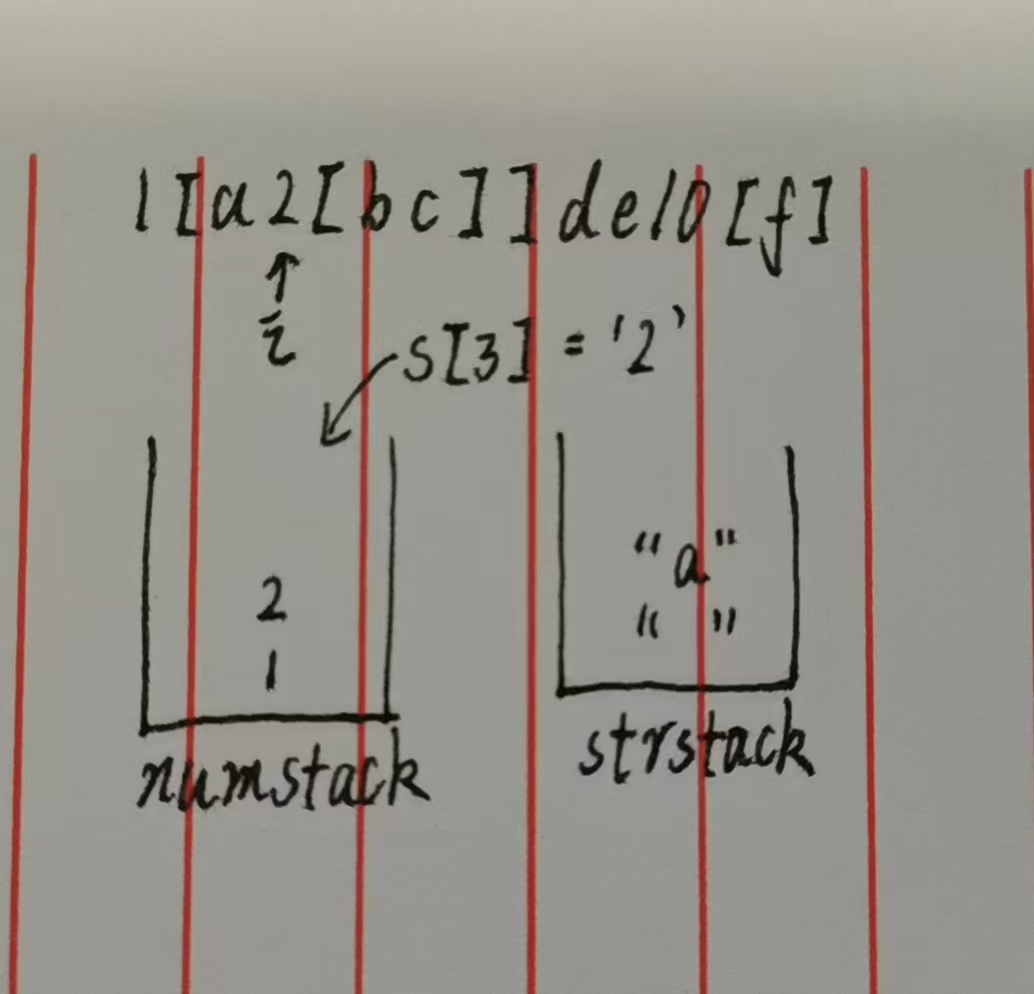
步骤3:解析数字 2(i=3)
- 字符
s[3] = '2',触发数字解析逻辑:- 解析完整数字:
an = 2,解析后i自增到4; - 将数字
2压入numstack→numstack = [1, 2]。
- 解析完整数字:
此时栈状态如下图👇:
步骤4:解析左括号 [ 与字母 bc(i=4)
- 字符
s[4] = '[',触发左括号逻辑:i自增到5,逐个解析字母:s[5] = 'b'、s[6] = 'c',得s到字符串"bc";- 将
"bc"压入strstack→strstack = ["", "a", "bc"]; - 解析后
i自增到7。
此时栈状态如下图👇:
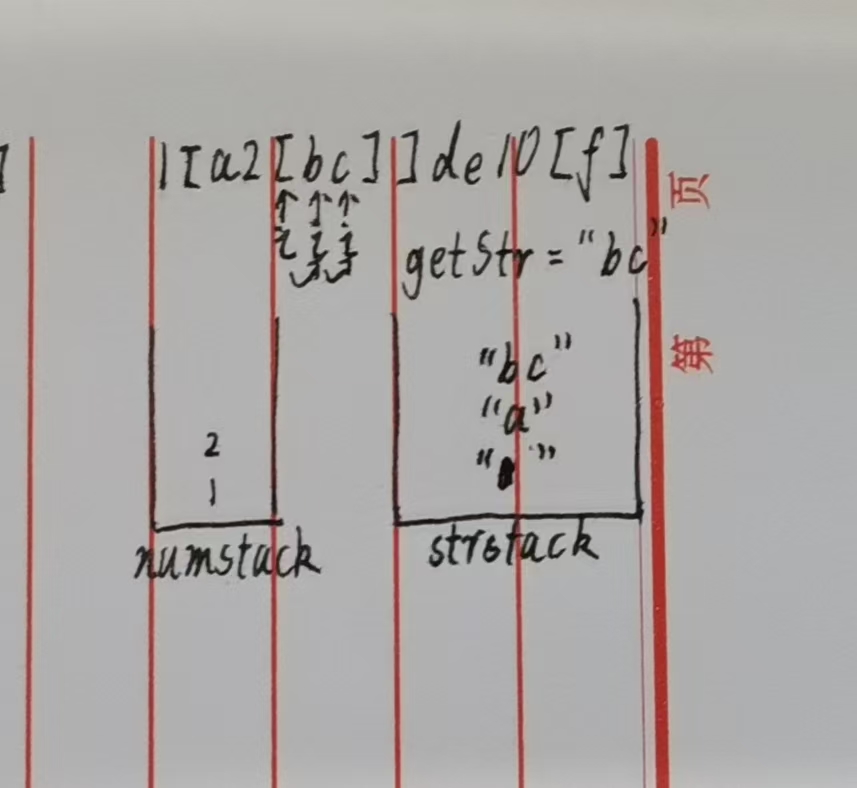
步骤5:解析右括号 ](i=7)→ 处理内层嵌套 2[bc]
- 字符
s[7] = ']',触发右括号逻辑进行拼接:- 弹出
numstack栈顶的2→numstack = [1]; - 弹出
strstack栈顶的"bc"→strstack = ["", "a"]; - 将
"bc"重复2次得到"bcbc",拼接到strstack新栈顶"a"后 →strstack = ["", "abcbc"]; i自增到8。
- 弹出
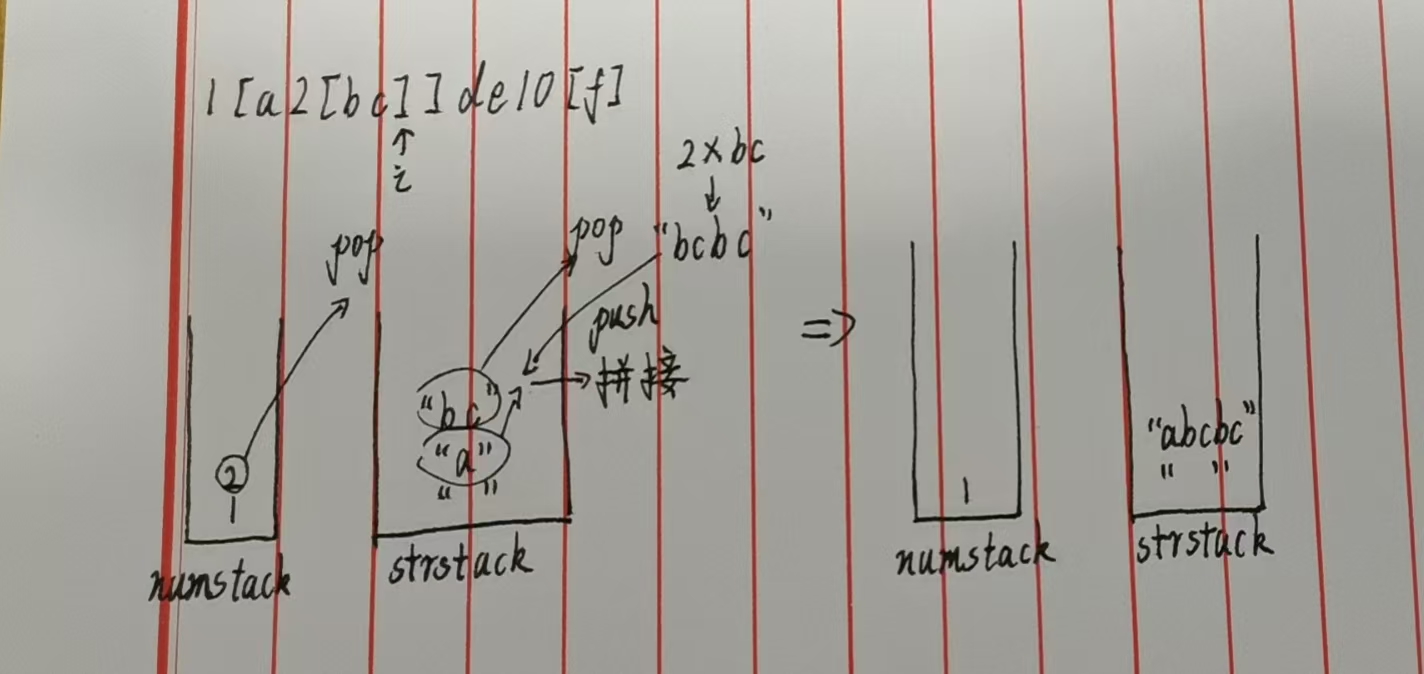
此时栈状态如下图👇:
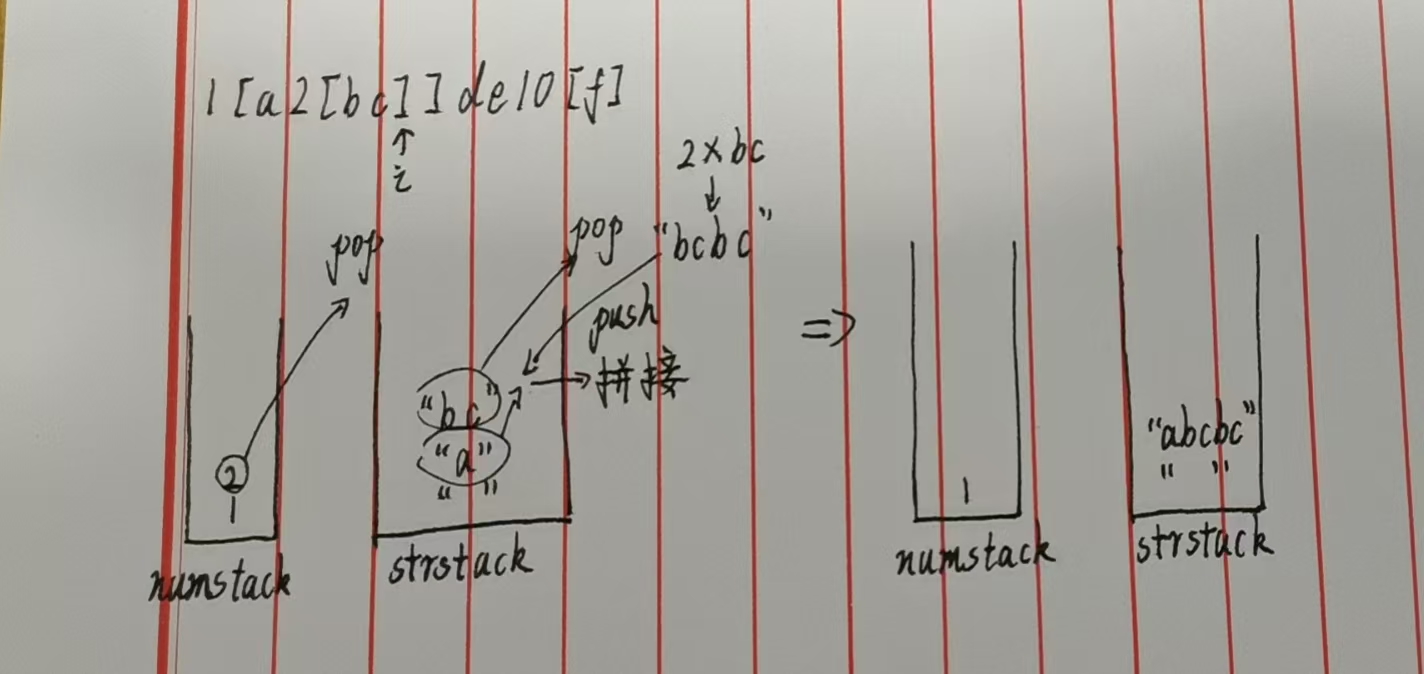
步骤6:解析右括号 ](i=8)→ 处理外层嵌套 1[abcbc]
- 字符
s[8] = ']',触发右括号逻辑进行拼接:- 弹出
numstack栈顶的1→numstack = []; - 弹出
strstack栈顶的"abcbc"→strstack = [""]; - 将
"abcbc"重复1次得到"abcbc",拼接到strstack栈顶空字符串后 →strstack = ["abcbc"]; i自增到9。
- 弹出
此时栈状态如下图👇:
这一步空字符串的作用就体现出来了,如果没有最开始的初始化空字符串这一步找不到操作统一,还需单独特判会非常麻烦。
步骤7:解析纯字母 de(i=9)
- 字符
s[9] = 'd'、s[10] = 'e',触发纯字母逻辑:- 解析得到字符串
"de"; - 将
"de"拼接到strstack栈顶"abcbc"后 →strstack = ["abcbcde"]; - 解析后
i自增到11。
- 解析得到字符串
此时栈状态如下图👇:
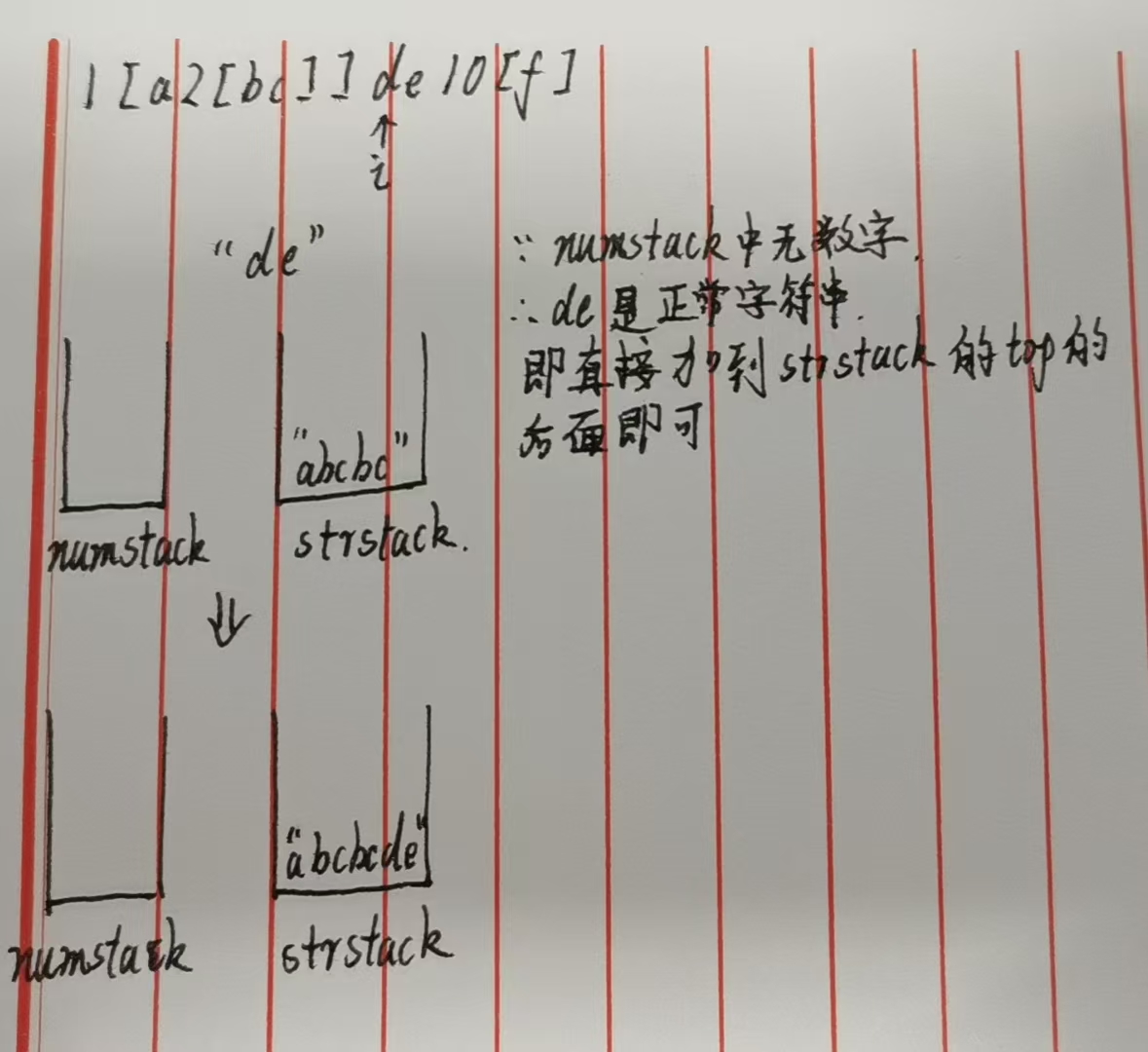
步骤8:解析多位数 10 与 10[f](i=11)
- 字符
s[11] = '1'、s[12] = '0',触发数字解析逻辑:- 解析多位数:先取
'1'→an=1,再取'0'→an=1*10+0=10,解析后i自增到13; - 将数字
10压入numstack→numstack = [10]。
- 解析多位数:先取
- 字符
s[13] = '[',触发左括号逻辑:i自增到14,解析字母'f'→ 得到"f";- 将
"f"压入strstack→strstack = ["abcbcde", "f"],i自增到15。
- 字符
s[15] = ']',触发右括号逻辑:- 弹出
numstack栈顶的10→numstack = []; - 弹出
strstack栈顶的"f"→strstack = ["abcbcde"]; - 将
"f"重复10次(ffffffffff),拼接到栈顶字符串后 →strstack = ["abcbcdeffffffffff"]; i自增到16,遍历结束。
- 弹出

最终结果
遍历完成后,strstack 栈顶的字符串即为解码结果:
"abcbcdeffffffffff"
细节注意
- 多位数处理:数字可能是1位(如3)、多位(如100),需循环解析完整数字,不能只取单个字符。
- 栈的初始化:字符串栈初始压入空字符串,避免拼接时处理栈空的边界情况。
- 字符串拼接优化:使用
reserve预分配内存,减少字符串拼接时的内存重新分配开销。 - 索引管理:确保索引同步推进,避免索引错乱。
- 嵌套边界:处理
]时,拼接结果要拼接到字符串栈的新栈顶,而非直接替换,保证外层嵌套能正确合并内层结果。
四、代码实现
cpp
class Solution {
public:
// 解析数字:处理多位数,i以引用传递保证索引同步
int getNumber(string& s,int& i)
{
int an = 0;
while(i < s.size() && s[i] >= '0' && s[i] <= '9')
{
an *= 10; // 处理十位、百位等高位
an += s[i++] - '0';// 转换字符为数字并推进索引
}
return an;
}
// 解析纯字母字符串,i以引用传递保证索引同步
string getStr(string& s,int& i)
{
string an;
while(i < s.size() && s[i] >= 'a' && s[i] <= 'z')
{
an += s[i++];
}
return an;
}
// 处理闭合符]:弹出栈顶数字和字符串,重复后拼接到上层
void Analysis(stack<int>& numstack, stack<string>& strstack)
{
int time = numstack.top();
numstack.pop();
string str = strstack.top();
strstack.pop();
// 预分配内存,优化拼接效率
string result;
result.reserve(str.length() * time);
// 重复指定次数并拼接到上层字符串
for (int i = 0; i < time; i++)
strstack.top() += str;
}
string decodeString(string s) {
stack<int> numstack; // 存储重复次数
stack<string> strstack; // 存储待拼接的字符串
strstack.push(""); // 初始空字符串,避免栈空
int i = 0;
while(i < s.size())
{
if(s[i] >= '0' && s[i] <= '9')
{
// 遇到数字:解析完整数字并压栈
numstack.push(getNumber(s,i));
}
else if(s[i] == '[')
{
// 遇到[:解析后续字母并压栈
i++;
strstack.push(getStr(s,i));
}
else if(s[i] == ']')
{
// 遇到]:处理拼接逻辑
Analysis(numstack,strstack);
i++;
}
else
{
// 遇到纯字母:直接拼接到栈顶
string add = getStr(s,i);
strstack.top() += add;
}
}
return strstack.top();
}
};复杂度分析
- 时间复杂度:O(n)。n为解码后的字符串总长度;遍历原字符串耗时O(m)(m为原字符串长度),字符串拼接的总操作次数等于解码后的长度n,整体由拼接操作主导,为O(n);
- 空间复杂度:O(n)。栈需要存储嵌套层级的数字和字符串,最坏情况下(如100[a100[b]])栈的存储量与解码后的长度n同阶。
五、总结
核心考点回顾
- 栈的"状态管理思维":将嵌套的解码逻辑转化为栈的层级状态,遇到闭合符时向上归并,是解题核心。
- 多类型字符的分层处理:数字、字母、括号分情况解析,保证逻辑清晰,避免边界错误。
- 性能优化意识:使用reserve预分配字符串内存,减少拼接时的内存开销,提升代码效率。
解题思路迁移
- 嵌套解析问题:只要是"先遇到外层、后处理外层"的嵌套结构(如括号匹配、公式计算、JSON解析),均可采用"栈+分层归并"的思路。
六、下题预告
六、下题预告
下一篇我们继续深挖栈的经典应用!接下来我们一起研究 力扣 946. 验证栈序列 这道高频栈题,我们一起彻底吃透栈在「入栈-出栈」序列验证场景的核心用法,从规则拆解到代码实现,一步步夯实栈结构的解题能力!
Doro 又爱着小花🌸奖励🌸坚持看到这里的你!栈"后进先出"的核心逻辑超实用,能掌握它在嵌套场景的使用技巧,你已经超厉害啦~
相信现在的你,对栈处理嵌套问题的思路已经胸有成竹了,下次遇到需要解析嵌套结构的题目,一定能第一时间想到用栈破局。把这篇内容收藏起来,后续刷题时遇到栈相关题型,随时翻查就能快速唤醒记忆。
如果你在今天的栈学习中有任何疑问 ------ 比如栈的状态管理、字符串拼接优化,或者有更优的解题思路,都可以发到评论区,博主看到会第一时间回复。
最后别忘了点个赞关注博主呀,你的支持就是博主持续更新优质算法内容的最大动力,我们下道题不见不散!
