[算法设计与分析-从入门到入土] 贪心算法
个人导航
知乎:https://www.zhihu.com/people/byzh_rc
CSDN:https://blog.csdn.net/qq_54636039
注:本文仅对所述内容做了框架性引导,具体细节可查询其余相关资料or源码
参考文章:各方资料
文章目录
- [[算法设计与分析-从入门到入土] 贪心算法](#[算法设计与分析-从入门到入土] 贪心算法)
- 个人导航
- [贪心算法Greedy Approach](#贪心算法Greedy Approach)
-
-
-
- [1.分数背包问题Fractional Knapsack](#1.分数背包问题Fractional Knapsack)
- 2.最短路径
- [3.最小耗费生成树Minimum Cost Spanning Trees](#3.最小耗费生成树Minimum Cost Spanning Trees)
- [4.文件压缩File Compression](#4.文件压缩File Compression)
-
-
贪心算法Greedy Approach
贪心算法常用于解决需要最大化或最小化某个量的优化问题,核心特点如下:
- 迭代过程:通过逐步构建解决方案,每一步都寻找局部最优解
- 最优性差异:部分场景下局部最优解可转化为全局最优解,部分场景无法得到全局最优
- 决策逻辑:基于少量计算做推测,不考虑后续影响 ,核心目标是产生最大即时收益
- 效率优势:每一步仅处理少量信息、完成少量工作,最终算法通常具有高效性
1.分数背包问题Fractional Knapsack
已知 n 件物品,参数如下:
- 物品大小: s 1 , s 2 , ... , s n s_{1},s_{2},\dots,s_{n} s1,s2,...,sn
- 物品价值: v 1 , v 2 , ... , v n v_{1},v_{2},\dots,v_{n} v1,v2,...,vn
- 背包容量: C C C
目标:确定一组非负实数 x 1 , x 2 , ... , x n x_{1},x_{2},\dots,x_{n} x1,x2,...,xn,使得总价值 ∑ i = 1 n x i v i \sum_{i=1}^{n} x_{i}v_{i} ∑i=1nxivi 最大,同时满足约束条件 ∑ i = 1 n x i s i ≤ C \sum_{i=1}^{n} x_{i}s_{i} \leq C ∑i=1nxisi≤C
贪心策略:
- 计算每个物品的价值-大小比率 : y i = v i s i y_i = \frac{v_i}{s_i} yi=sivi
- 按比率 y i y_i yi 降序排序物品
- 按排序顺序,尽可能多地将当前物品放入背包
2.最短路径
给定有向图 G = ( V , E ) G=(V,E) G=(V,E),每条边具有非负长度,指定源点 s s s
目的: 确定从源点 s s s 到 V V V 中其他所有顶点的最短距离
贪心策略: Dijkstra 算法
假设 V = { 1 , 2 , ... , n } V=\{1,2,...,n\} V={1,2,...,n} 且源点 s = 1 s=1 s=1
将顶点集合划分为两个子集,逐步扩充"距离已确定"的顶点集合,更新剩余顶点的最短路径标签
- 子集 X X X:到源点距离已确定的顶点集合(初始 X = { 1 } X=\{1\} X={1})
- 子集 Y Y Y:剩余所有顶点集合(初始 Y = { 2 , 3 , ... , n } Y=\{2,3,\dots,n\} Y={2,3,...,n})
- 标签 λ [ y ] \lambda[y] λ[y]( y ∈ Y y \in Y y∈Y):表示仅经过 X X X 中顶点到达 y y y 的最短路径长度
λ [ 1 ] = 0 , λ [ i ] = { length ( 1 , i ) if ( 1 , i ) ∈ E ∞ if ( 1 , i ) ∉ E , 2 ≤ i ≤ n \lambda[1]=0,\quad\lambda[i]=\left\{ \begin{array}{ll} \text{length}(1,i) & \text{if } (1,i) \in E \\ \infty & \text{if } (1,i) \notin E \end{array} \right.,\quad 2 \leq i \leq n λ[1]=0,λ[i]={length(1,i)∞if (1,i)∈Eif (1,i)∈/E,2≤i≤n
流程:
-
从 Y Y Y 中选择 λ \lambda λ 值最小的顶点 y y y,将其移至 X X X
-
对所有满足 w ∈ Y w \in Y w∈Y 且 ( y , w ) ∈ E (y,w) \in E (y,w)∈E 的顶点 w w w,更新标签:
λ [ w ] = min { λ [ w ] , λ [ y ] + length ( y , w ) } \lambda[w] = \min\{\lambda[w], \lambda[y] + \text{length}(y,w)\} λ[w]=min{λ[w],λ[y]+length(y,w)} -
重复步骤 1-2,直至 Y Y Y 为空
时间复杂度: Θ ( n 2 ) \Theta(n^2) Θ(n2)
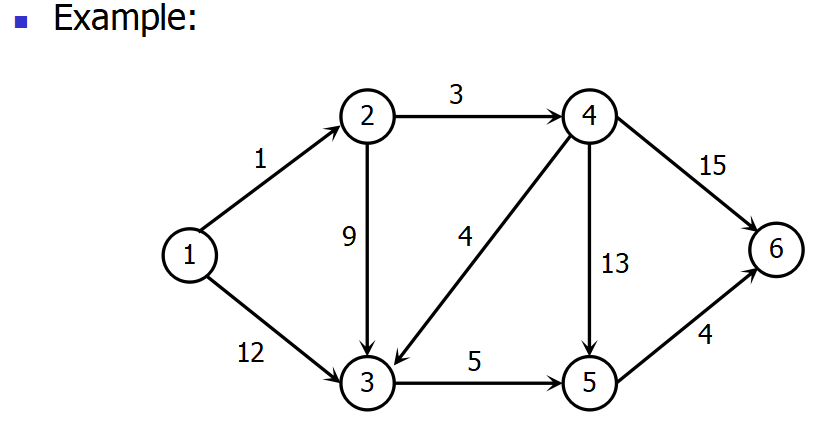
例子:
3.最小耗费生成树Minimum Cost Spanning Trees
维护一个由多棵生成树构成的森林,通过逐步合并树木,最终形成一棵生成树(无环、包含所有顶点、总权重最小)
-
将图中所有边按权重升序排序
-
初始化森林 ( V , T ) (V, T) (V,T),其中 T = ∅ T=\varnothing T=∅(仅包含所有顶点,无任何边)
-
迭代处理排序后的边 e ∈ E − T e \in E-T e∈E−T
- 若将 e 加入 T 后不会形成环,则将 e 纳入 T
- 否则舍弃 e
-
重复步骤 3,直至 (V, T) 成为一棵完整的树
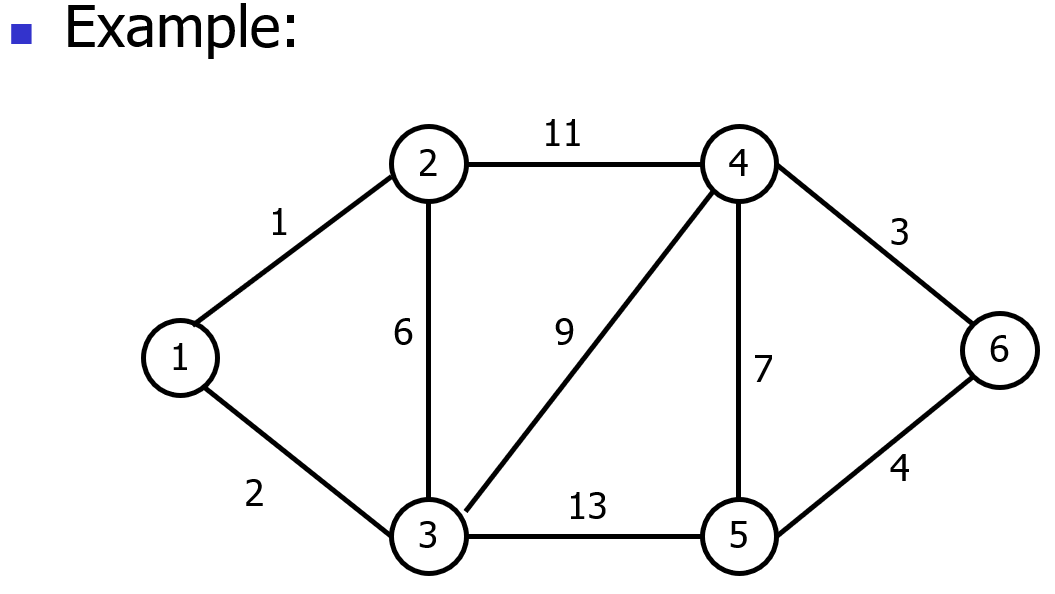
例子:
4.文件压缩File Compression
-> 哈夫曼编码(前缀码构建)
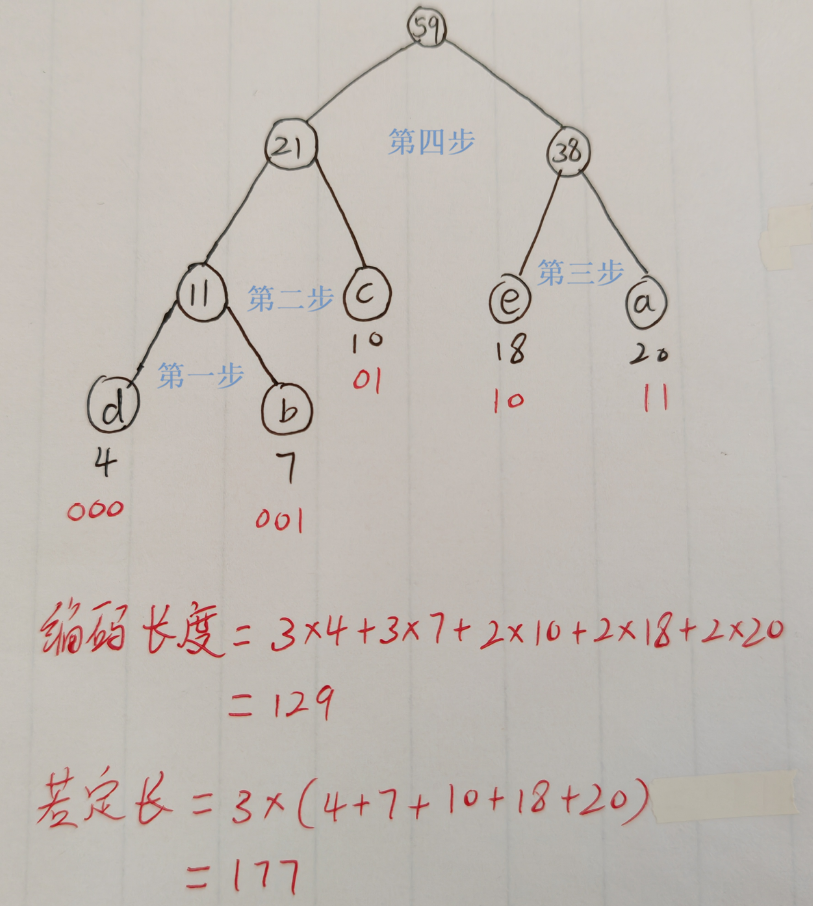
将由字符集合 C = { c 1 , c 2 , ... , c n } C=\{c_1,c_2,\dots,c_n\} C={c1,c2,...,cn} 组成的文件进行压缩, f ( c j ) f(c_j) f(cj) 表示字符 c j c_j cj 的出现频率
为提升压缩效率,采用变长编码
- 高频字符分配较短编码
- 低频字符分配较长编码
- 约束条件:任一字符的编码不得是其他字符编码的前缀(前缀码),保证解码唯一性
基于完全二叉树构建编码:内部节点含 0/1 标记的分支
- 叶节点对应字符
- 根节点到叶节点的 0/1 序列即为该字符的编码
贪心步骤:
- 从初始字符集合 C C C 开始
- 选取集合中出现频率最小的两个字符 c i c_i ci 和 c j c_j cj
- 创建新节点 c c c,其频率为 c i c_i ci 和 c j c_j cj 的频率之和,令 c i c_i ci 和 c j c_j cj 为 c c c 的子节点
- 更新集合: C = ( C − { c i , c j } ) ∪ { c } C = (C - \{c_i,c_j\}) \cup \{c\} C=(C−{ci,cj})∪{c}
- 重复步骤 2-4,直至集合 C 中仅剩一个字符(即二叉树的根节点)
例子: