LeetCode 437. 路径总和 III

题目描述

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例

示例 1：

复制代码

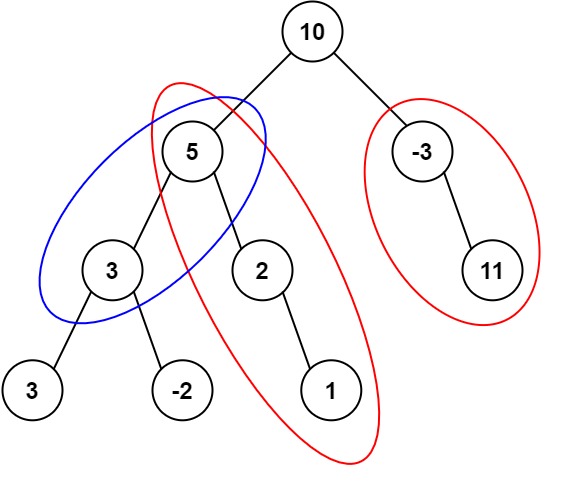
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

复制代码

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

解法

1.前缀和 + DFS

解题思路

如果二叉树是一条链，本题就和 560. 和为 K 的子数组完全一样了：统计有多少个非空连续子数组的元素和恰好等于 targetSum。所以你必须先弄明白 560 题（特殊情况），再来做本题（一般情况）。560 题的做法见 LeetCode 560. 和为 K 的子数组。

我们要解决的问题是：DFS 遍历这棵树，遍历到节点 node 时，假设 node 是路径的终点，那么有多少个起点，满足起点到终点 node 的路径总和恰好等于 targetSum？

和 560 题一样的套路：一边遍历二叉树，一边用哈希表 cnt 统计前缀和（从根节点开始的路径和）的出现次数。设从根到终点 node 的路径和为 s，那么起点的个数就是 cnt $s-targetSum$ ，加入答案。对比 560 题，我们在枚举子数组的右端点（终点），统计有多少个左端点（起点），做法完全一致。

cpp 复制代码

class Solution {
public:
    int pathSum(TreeNode* root, int targetSum) {
        int ans = 0;
        unordered_map <long long,int> m{{0,1}};
        auto dfs = [&](this auto&& dfs,TreeNode* node, long long s){
            if(node == nullptr) return;
            s += node -> val;
            if(m.find(s - targetSum) != m.end()) ans += m[s - targetSum];
            m[s] ++;
            dfs(node -> left,s);
            dfs(node -> right,s);
            m[s] --;
        };
        dfs(root,0);
        return ans;
    }
};

时间复杂度O（N），空间复杂度O（N）