文章目录
摘要
本周重复学习了Transformer的内容,内容比较多,从机制到步骤通过pytorch代码进行实现。
Abstract
This week, I reviewed the content on Transformers, which was quite extensive, and implemented everything from the mechanism to the steps using PyTorch code.
1 Transformer
在之前了解过注意力机制,但是在学习到语言模型时,发现对注意力机制还是理解不够到位。所以本周重新对注意力机制进行学习。注意力机制就是把焦点聚焦在重要的事物上。
做法:
1、输入查询(query,Q),比如在淘宝输入"笔记本"
2、计算相似性,淘宝根据查询Q,和后台的所有商品的关键字Key或者title来对比,相似性越高,推送的可能性越高。
3、得到价值,这个物品在算法的价值,一件商品物美价廉、评论好、购买多,那么这件物品价值就会更高。
4、计算带权重的价值,相似性(K)和价值(V)相乘,值越高的越重要。
将词向量和位置信息相加,这个词就有了位置信息。
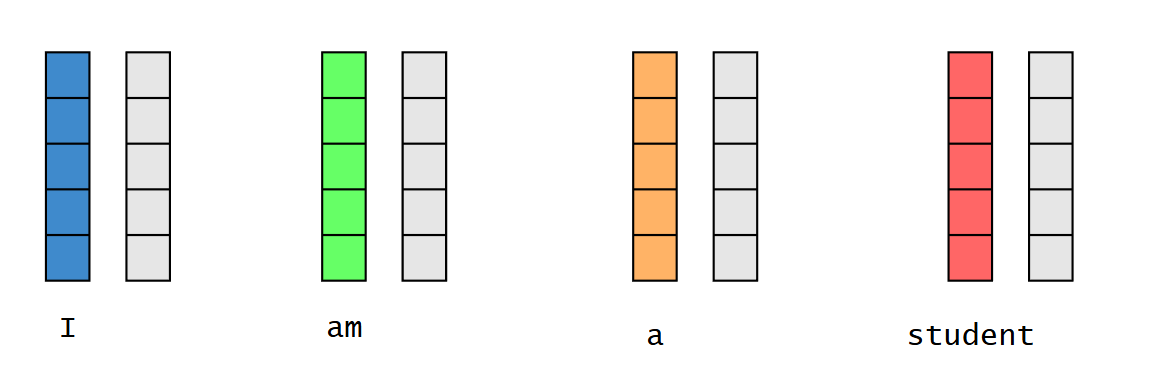
通过权重矩阵 w q 、 w k 、 w v w_q、w_k、w_v wq、wk、wv与词向量相乘,得到每个词的 q 、 k 、 v q、k、v q、k、v权重向量。
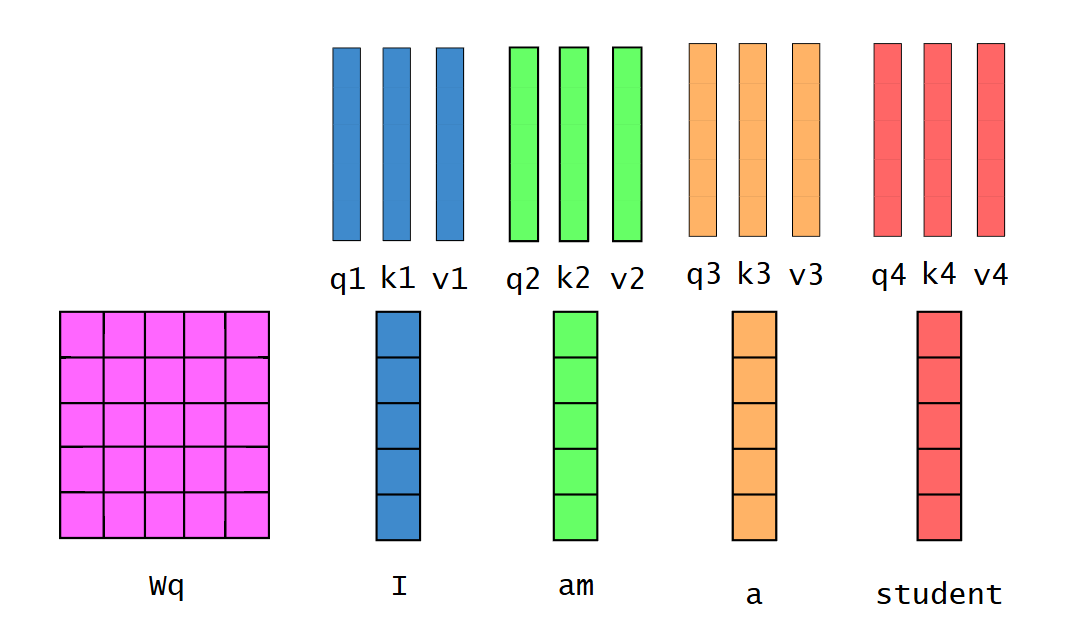
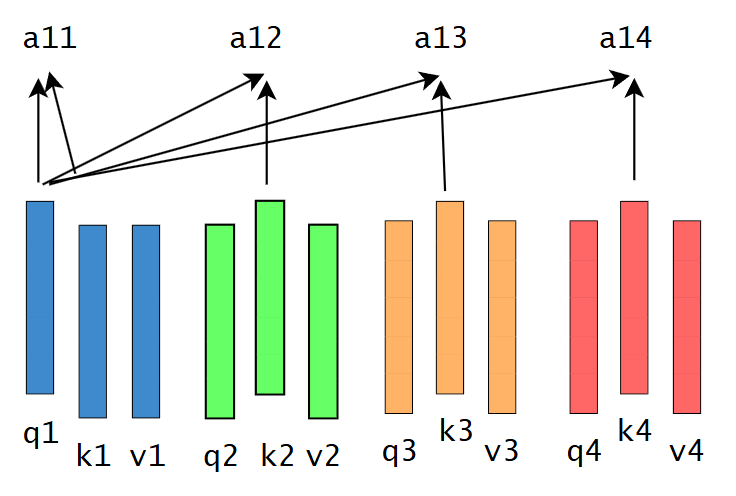
从第一个词的角度与自己、其他词的k向量进行点积,代表自己与自己、与其他词的相似度。
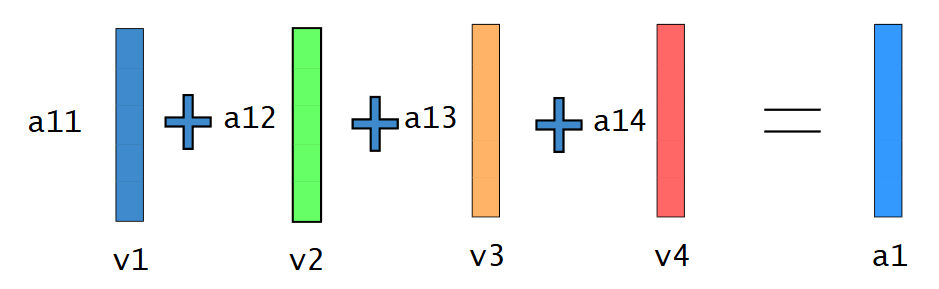
按照相似度与v向量相乘再相加最后得到的a向量包含词的上下文信息。
1.1 Scaled Dot-Product Attention
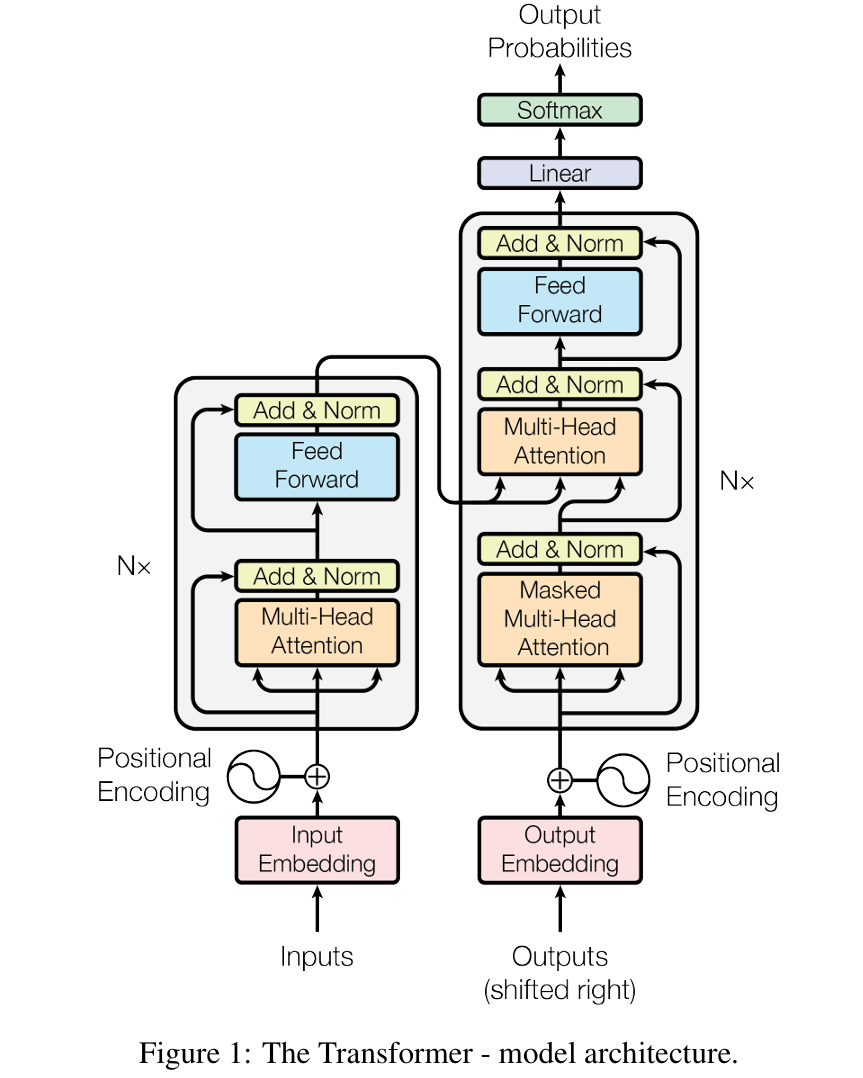
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V Attention(Q,K,V)=softmax(dk QKT)V
分子 d k \sqrt{d_k} dk 为了解决梯度太低的问题,Q为多个query的矩阵。
在计算 q t q_t qt之前只能看见前面 k 1 , . . . , k t − 1 k_1,...,k_{t-1} k1,...,kt−1的信息,将 k t − 1 k_{t-1} kt−1后面的值乘上一个很大的负权重,这样后面的值的影响就很低。
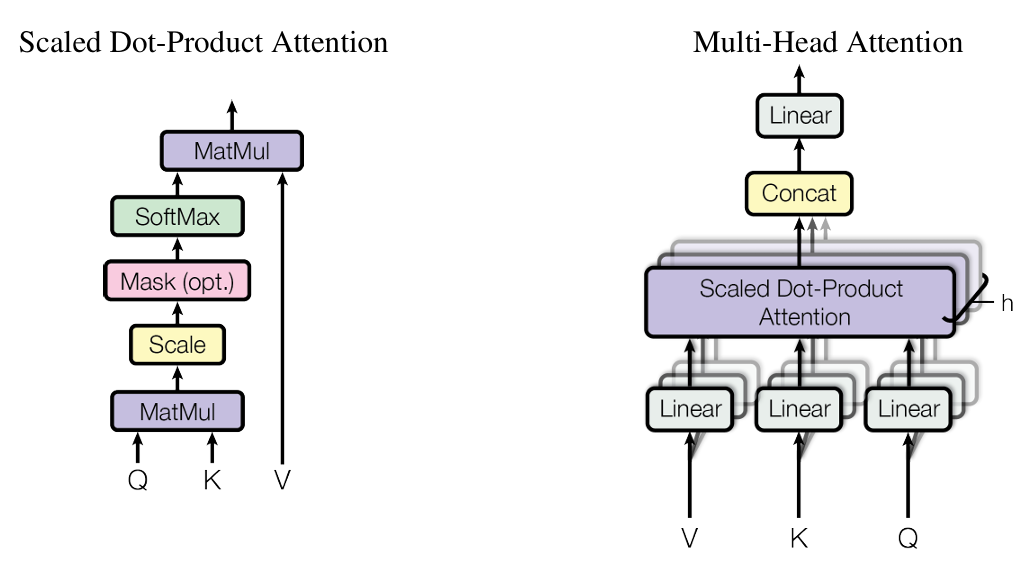
1.2 Multi-head Attention
经过不同的权重矩阵得到不同的QKV,不同的词在不同的模式下理解是不一样的。
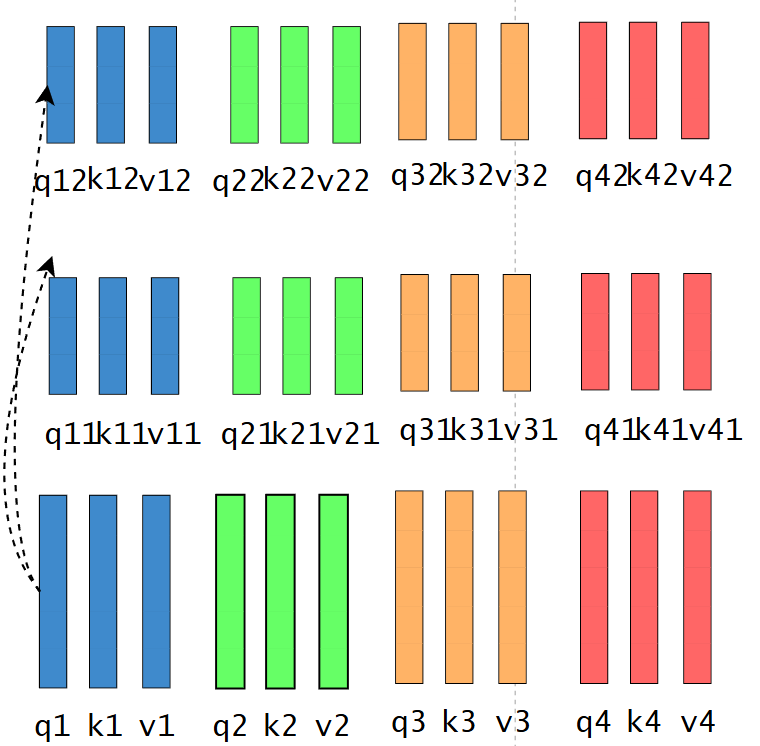
经过相同的相似度计算流程,再将得到的向量拼在一起,就得到和刚刚一样长的向量。
M u l t i H e a d ( Q , K , V ) = C o n c a t ( h e a d 1 , ⋅ , h e a d h ) W O w h e r e h e a d i = A t t e n t i o n ( Q , W i Q , K W i K , V W i V ) MultiHead(Q,K,V)=Concat(head_1,\cdot,head_h)W^O \\ where head_i=Attention(Q,W_i^Q,KW_i^K,VW_i^V) MultiHead(Q,K,V)=Concat(head1,⋅,headh)WOwhereheadi=Attention(Q,WiQ,KWiK,VWiV)
2 基础知识
标量、向量、矩阵、张量
标量:一个人身高175cm,体重70kg,年龄25岁。这三个数字都是标量。
向量:一个人的特征(175,70,25)组成的称为向量,向量之间是有相关性的,另一个人的向量(170,70,25),可以说这两个人比较相似。
矩阵: R 2 × 3 = ( 175 70 25 170 70 25 ) R^{2\times 3}=\begin{pmatrix}175 & 70 & 25 \\ 170 & 70 & 25\end{pmatrix} R2×3=(17517070702525)多个向量组成一个矩阵,上面代表有两个样本,每个样本三个特征。
张量:标量可以说是一个0维张量,向量是一个1维张量,矩阵是一个二维张量,两个矩阵拼合是一个三维张量 R 2 × 2 × 3 = ( [ 175 70 25 170 70 25 ] [ 175 70 25 170 70 25 ] ) R^{2\times 2 \times 3}=\begin{pmatrix} \begin{bmatrix}175 & 70 & 25 \\ 170 & 70 & 25\end{bmatrix} \\ \begin{bmatrix}175 & 70 & 25 \\ 170 & 70 & 25\end{bmatrix} \end{pmatrix} R2×2×3= [17517070702525][17517070702525]
总结
本周学习的内容比较基础,但是里面有很多重要的东西需要理解。