近世代数（抽象代数）详细笔记--域

第五章：域的扩张

5.1向量空间(线性空间)

为了较深入地研究域,特别是研究扩域,有必要将线性代数中已学过的数域上的向量空间的概念推广到任意域上.

定义 :线性空间

设 V V V是一个带有加法 (记作 " + + +" ) 运算的非空集合, F F F 是一个域. 如果 V V V关于加法运算构成一个交换群 , 并且对每个 k ∈ F , v ∈ V k \in F, v \in V k∈F,v∈V, 在 V V V中可唯一地确定一个元素 k v kv kv(称为 k k k与 v v v的标量乘法), 使得对所有的 k , l ∈ F , u , v ∈ V k,l \in F, u,v \in V k,l∈F,u,v∈V, 满足

(1) ( k l ) v = k ( l v ) (kl)v = k(lv) (kl)v=k(lv);

(2) ( k + l ) v = k v + l v (k + l)v = kv + lv (k+l)v=kv+lv;

(3) k ( u + v ) = k u + k v k(u + v) = ku + kv k(u+v)=ku+kv;

(4) 1 v = v 1v = v 1v=v,

则称 V V V为域 F F F上的一个向量空间 (vector space) 或线性空间 (linear space). 向量空间中的元素称为向量 (vector), 域中的元素称为标量或纯量(scalar), 域 F F F称为向量空间的基域.

定义 ：子空间

设 V V V是域 F F F上的向量空间， U U U是 V V V的非空子集。如果 U U U关于 V V V的运算也构成 F F F上的向量空间，则称 U U U为 V V V的子空间。

定义 ：线性相关

设 v 1 , v 2 , ⋯   , v n v_1, v_2, \cdots, v_n v1,v2,⋯,vn是向量空间 V V V的一组向量，如果存在不全为零的元素 k 1 , k 2 , ⋯   , k n ∈ F k_1, k_2, \cdots, k_n \in F k1,k2,⋯,kn∈F，使得
k 1 v 1 + k 2 v 2 + ⋯ + k n v n = 0 , k_1v_1 + k_2v_2 + \cdots + k_nv_n = 0, k1v1+k2v2+⋯+knvn=0,

则称向量组 v 1 , v 2 , ⋯   , v n v_1, v_2, \cdots, v_n v1,v2,⋯,vn在 F F F上线性相关 （linearly dependent）。如果一个向量组在 F F F上不是线性相关的，则称这个向量组在 F F F上线性无关（linearly independent）。

定义 ：基

设 V V V是 F F F上的向量空间， B B B是 V V V的一个非空子集。如果 B B B中任一有限子集都在 F F F上线性无关，且 B B B张成 V V V，则称 B B B为 V V V的基。

定理 5.1.1

如果 { u 1 , u 2 , ⋯   , u m } \{u_1,u_2,\cdots,u_m\} {u1,u2,⋯,um}和 { w 1 , w 2 , ⋯   , w n } \{w_1,w_2,\cdots,w_n\} {w1,w2,⋯,wn}都是域 F F F上向量空间 V V V的基，那么 m = n m = n m=n。

5.2扩域

定义：极小多项式

设 a 是域 F 的扩域中的一个元素。如果 a 是 F 上的代数元 （即存在一个非零多项式 f(x) \in F[x] 使得 f(a) = 0），那么 a 在 F 上的极小多项式 p(x) 是满足以下条件的唯一多项式：

1. 首一的：最高次项的系数为 1。
2. 不可约的：不能在 F 上分解为两个次数更低的多项式的乘积。
3. 以 a 为根：p(a) = 0。
4. 次数最低：它是所有以 a 为根的多项式中次数最小的。

理解 ：有些类似 λ \lambda λ矩阵中提到的最小多项式，简单来说，极小多项式就是刻画代数元 a a a 相对于基域 F F F 的"最精简"的代数方程。

定义 :扩域

设 F F F和 E E E是两个域. 如果 F ⊆ E F \subseteq E F⊆E，并且 F F F中的运算就是 E E E的运算在 F F F上的限制，则称 E E E为域 F F F的扩域 (extension field)，而称 F F F为 E E E的子域。记作： E / F E/F E/F

定理：5.2.1

设 F F F是一个域， S 1 S_1 S1和 S 2 S_2 S2是 F F F的两个非空子集。则： F ( S 1 ) ( S 2 ) = F ( S 1 ∪ S 2 ) = F ( S 2 ) ( S 1 ) F(S_1)(S_2) = F(S_1 \cup S_2) = F(S_2)(S_1) F(S1)(S2)=F(S1∪S2)=F(S2)(S1)

其中 F ( S ) F(S) F(S)表示域 F F F添加集合 S S S所生成的域（即 F F F与 S S S中元素的所有有理函数构成的域）。

理解：

F ( S 1 ) ( S 2 ) F(S_1)(S_2) F(S1)(S2)表示先添加子集 S 1 S_1 S1到 F F F中生成域 F ( S 1 ) F(S_1) F(S1)，然后再添加子集 S 2 S_2 S2到 F ( S 1 ) F(S_1) F(S1)中生成域 F ( S 1 ) ( S 2 ) F(S_1)(S_2) F(S1)(S2)。 F ( S 2 ) ( S 1 ) F(S_2)(S_1) F(S2)(S1)表示先添加 S 2 S_2 S2再添加 S 1 S_1 S1所生成的域。 F ( S 1 ∪ S 2 ) F(S_1 \cup S_2) F(S1∪S2)表示一次性添加 S 1 S_1 S1和 S 2 S_2 S2中所有元素到 F F F所生成的域。 定理表明：无论先添加哪个子集，最终生成的域都是相同的；分步添加（无论顺序）与直接添加并集的结果一致。

举例：

(1) S = { a } S = \{a\} S={a}，其中 a ∈ E a \in E a∈E。记
F ( { a } ) = F ( a ) . F(\{a\}) = F(a). F({a})=F(a).

称 F ( a ) F(a) F(a) 为 F F F 的==单扩域 ==或单扩张 (simple extension)。

F ( a ) F(a) F(a) 是由 E E E 中哪些元素组成的呢？首先，因为 a ∈ F ( a ) a \in F(a) a∈F(a)，有 a k ∈ F ( a ) a^k \in F(a) ak∈F(a) ( k ∈ N k \in \mathbb{N} k∈N)，因此对任意的 f ( x ) ∈ F [ x ] f(x) \in F[x] f(x)∈F[x]， f ( a ) ∈ F ( a ) f(a) \in F(a) f(a)∈F(a)。又对任意的 g ( x ) ∈ F [ x ] g(x) \in F[x] g(x)∈F[x]，如果 g ( a ) ≠ 0 g(a) \neq 0 g(a)=0，则 1 g ( a ) ∈ F ( a ) \frac{1}{g(a)} \in F(a) g(a)1∈F(a)（域对除法封闭）。

从而定义集合：
F ~ = { f ( a ) g ( a ) ∣ f ( x ) , g ( x ) ∈ F [ x ] , g ( a ) ≠ 0 } ⊆ F ( a ) . \widetilde{F} = \left\{ \frac{f(a)}{g(a)} \ \bigg| \ f(x), g(x) \in F[x], g(a) \neq 0 \right\} \subseteq F(a). F ={g(a)f(a) f(x),g(x)∈F[x],g(a)=0}⊆F(a).

由域的定义直接验证可知， F ~ \widetilde{F} F 是一个域，且 F ⊆ F ~ F \subseteq \widetilde{F} F⊆F ， a ∈ F ~ a \in \widetilde{F} a∈F ，从而
F ~ = F ( a ) , \widetilde{F} = F(a), F =F(a),

即
F ( a ) = { f ( a ) g ( a ) ∣ f ( x ) , g ( x ) ∈ F [ x ] , g ( a ) ≠ 0 } . F(a) = \left\{ \frac{f(a)}{g(a)} \ \bigg| \ f(x), g(x) \in F[x], g(a) \neq 0 \right\}. F(a)={g(a)f(a) f(x),g(x)∈F[x],g(a)=0}.

理解 ：
F ( a ) F(a) F(a)就是所有在 a a a 处有定义的有理函数的集合。换句话说，它是 F F F 上所有有理函数在 a a a 处的取值的集合。

• 当 a a a 是代数元时，这个表示可以简化
  F ( a ) = { c 0 + c 1 a + c 2 a 2 + ⋯ + c n − 1 a n − 1 ∣ c i ∈ F } F(a) = \{c_0 + c_1a + c_2a^2 + \cdots + c_{n-1}a^{n-1} \mid c_i \in F\} F(a)={c0+c1a+c2a2+⋯+cn−1an−1∣ci∈F}

  换句话说：

  • F ( a ) F(a) F(a) 是 F F F 上的 n n n 维向量空间
  • 基为 { 1 , a , a 2 , ... , a n − 1 } \{1, a, a^2, \ldots, a^{n-1}\} {1,a,a2,...,an−1}
  • 不需要分式形式，所有元素都是次数小于 n n n 的多项式

• 当 a a a 是超越元时，这个表示就是最简形式

(2) S = { a 1 , a 2 , ⋯   , a s } S = \{a_1, a_2, \cdots, a_s\} S={a1,a2,⋯,as}，其中 a i ∈ E a_i \in E ai∈E ( i = 1 , 2 , ⋯   , s i = 1, 2, \cdots, s i=1,2,⋯,s)。记
F ( S ) = F ( a 1 , a 2 , ⋯   , a s ) . F(S) = F(a_1, a_2, \cdots, a_s). F(S)=F(a1,a2,⋯,as).

称 F ( a 1 , a 2 , ⋯   , a s ) F(a_1, a_2, \cdots, a_s) F(a1,a2,⋯,as) 为 F F F 的添加 E E E 的元素 a 1 , a 2 , ⋯   , a s a_1, a_2, \cdots, a_s a1,a2,⋯,as 所得的扩域。由定理 5.2.1 知，
F ( a 1 , a 2 , ⋯   , a s ) = F ( a 1 ) ( a 2 ) ⋯ ( a s ) . F(a_1, a_2, \cdots, a_s) = F(a_1)(a_2) \cdots (a_s). F(a1,a2,⋯,as)=F(a1)(a2)⋯(as).

这说明，添加有限个元素于 F F F 所得到的扩域可通过逐次的单扩张而得到。

与 (1) 类似，可得
F ( a 1 , a 2 , ⋯   , a s ) = { f ( a 1 , a 2 , ⋯   , a s ) g ( a 1 , a 2 , ⋯   , a s ) ∣ f , g ∈ F [ x 1 , x 2 , ⋯   , x s ] , g ( a 1 , a 2 , ⋯   , a s ) ≠ 0 } . F(a_1, a_2, \cdots, a_s) = \left\{ \frac{f(a_1, a_2, \cdots, a_s)}{g(a_1, a_2, \cdots, a_s)} \ \bigg| \ f, g \in F[x_1, x_2, \cdots, x_s], g(a_1, a_2, \cdots, a_s) \neq 0 \right\}. F(a1,a2,⋯,as)={g(a1,a2,⋯,as)f(a1,a2,⋯,as) f,g∈F[x1,x2,⋯,xs],g(a1,a2,⋯,as)=0}.

层次关系：

定义 ：有限扩域与扩张次数

设 E E E是 F F F的扩域. 如果 E E E作为 F F F上的向量空间是有限维的, 则称 E E E是 F F F的有限扩域 或有限扩张(finite extension), 否则称 E E E为 F F F的无限扩域 或无限扩张(infinite extension). E E E在 F F F上的维数 dim ⁡ F E \dim_F E dimFE称为 E E E关于 F F F的扩张次数(degree of extension), 记作 [ E : F ] [E:F] [E:F], 即 [ E : F ] = dim ⁡ F ( E ) . [E:F] = \dim_F(E). [E:F]=dimF(E).

定理 5.2.2

设 K K K是域 E E E的有限扩域， E E E是域 F F F的有限扩域，则 K K K是域 F F F的有限扩域，且 [ K : F ] = [ K : E ] ⋅ [ E : F ] . [K:F] = [K:E] \cdot [E:F]. [K:F]=[K:E]⋅[E:F].

定理 : 5.2.3（域论基本定理，Kronecker(1887)）

设 F F F是域， f ( x ) f(x) f(x)是 F [ x ] F[x] F[x]中次数大于零的多项式，那么存在 F F F的扩域，使得 f ( x ) f(x) f(x)在此扩域中有根。

5.3代数扩张

定义：有理函数

有理函数是多项式的商，形式为：

f ( x ) g ( x ) \frac{f(x)}{g(x)} g(x)f(x) 其中 f ( x ) , g ( x ) ∈ F [ x ] f(x), g(x) \in F[x] f(x),g(x)∈F[x]， g ( x ) ≠ 0 g(x) \neq 0 g(x)=0 其中 F [ x ] F[x] F[x] 表示域 F F F 上的一元多项式环，

核心是"多项式除以非零多项式"的形式。

理解：（三个角度）

1. 形式分式的观点

   有理函数的本质是形式上的分式 ，重点关注其代数结构（如运算规则、等价性），而非作为"函数"的分析性质（如定义域、连续性）。例如， x 2 − 1 x − 1 \frac{x^2 - 1}{x - 1} x−1x2−1 与 x + 1 x + 1 x+1 作为有理函数是等价的（可通过约分得到），即使前者在 x = 1 x = 1 x=1 处"无定义"，但从代数结构上二者一致。

2. 与有理数的类比

   有理函数的定义和性质可通过与有理数类比理解，二者都是"两个代数结构的商"，运算规则完全平行：

有理数 Q \mathbb{Q} Q	有理函数域 F ( x ) F(x) F(x)
形式: m n \frac{m}{n} nm，其中 m , n ∈ Z m, n \in \mathbb{Z} m,n∈Z（整数环）， n ≠ 0 n \neq 0 n=0	形式: f ( x ) g ( x ) \frac{f(x)}{g(x)} g(x)f(x)，其中 f ( x ) , g ( x ) ∈ F [ x ] f(x), g(x) \in F[x] f(x),g(x)∈F[x]（多项式环）， g ( x ) ≠ 0 g(x) \neq 0 g(x)=0
等价性: 约分（消去分子分母的公因子），如 6 8 = 3 4 \frac{6}{8} = \frac{3}{4} 86=43	等价性: 约分（消去分子分母的公因式），如 x 2 − 1 x 2 + x − 2 = ( x − 1 ) ( x + 1 ) ( x − 1 ) ( x + 2 ) = x − 1 x + 2 \frac{x^2 - 1}{x^2 + x - 2} = \frac{(x - 1)(x + 1)}{(x - 1)(x + 2)} = \frac{x - 1}{x + 2} x2+x−2x2−1=(x−1)(x+2)(x−1)(x+1)=x+2x−1
运算规则: 加法（通分）、乘法（分子乘分子，分母乘分母）	运算规则: 加法（通分）、乘法（分子乘分子，分母乘分母），与有理数完全一致

3. 在域扩张中的意义
   域扩张中， F ( a ) = { f ( a ) g ( a ) ∣ f ( x ) , g ( x ) ∈ F [ x ] , g ( a ) ≠ 0 } F(a) = \left\{ \frac{f(a)}{g(a)} \ \bigg| \ f(x), g(x) \in F[x], g(a) \neq 0 \right\} F(a)={g(a)f(a) f(x),g(x)∈F[x],g(a)=0} 是核心构造，其与有理函数的关系可概括为：

• F ( a ) F(a) F(a) 中的每个元素，本质是有理函数在 a a a 处的取值 （将有理函数 f ( x ) g ( x ) \frac{f(x)}{g(x)} g(x)f(x) 中的变量 x x x 替换为域扩张中的元素 a a a）；
• 条件 g ( a ) ≠ 0 g(a) \neq 0 g(a)=0 是关键：确保分式在扩域 E E E 中有意义（分母不为零，避免无定义）；
• F ( a ) F(a) F(a) 的本质是"包含域 F F F 和元素 a a a 的最小子域"，而有理函数的商结构恰好保证了它对四则运算封闭（满足域的定义）。

定义 :代数元，超越元，代数扩张，超越扩张

设 E E E为域 F F F的扩域， a ∈ E a \in E a∈E，

如果存在 F F F上的非零多项式 f ( x ) f(x) f(x)（ F [ x ] F[x] F[x]中的多项式），使得 f ( a ) = 0 f(a) = 0 f(a)=0，则称 a a a为 F F F上的一个代数元(algebraic element)。

如果 a a a不是 F F F上的代数元，那么称 a a a为 F F F上的一个超越元(transcendental element)。

如果 F F F的扩域 E E E中的每个元素都是 F F F上的代数元，则称 E E E是 F F F的代数扩张(algebraic extension)。

如果 E E E不是 F F F的代数扩张，则称 E E E为 F F F的超越扩张(transcendental extension)。

有理数域上的代数元称为代数数，不是代数数的数称为超越数。

定理:5.3.1

设 E E E是域 F F F的扩域， a ∈ E a \in E a∈E。

(1) 如果 a a a是 F F F上的超越元，则 F ( a ) F(a) F(a)同构于 F [ x ] F[x] F[x]的商域 F ( x ) F(x) F(x)；

(2) 如果 a a a是 F F F上的代数元，则 F ( a ) F(a) F(a)同构于 F [ x ] / ⟨ p ( x ) ⟩ F[x]/\langle p(x) \rangle F[x]/⟨p(x)⟩（其中 p ( x ) p(x) p(x)是 a a a在域 F F F上的极小多项式）。

推论1 :

设 a a a是 F F F上的代数元， p ( x ) p(x) p(x)是 F F F上的一个首一多项式，则下列条件等价：

(1) p ( x ) p(x) p(x)是 a a a在域 F F F上的极小多项式 ；

(2) p ( x ) p(x) p(x)在 F F F上不可约，且 p ( a ) = 0 p(a) = 0 p(a)=0；

(3) p ( x ) p(x) p(x)是 F F F上以 a a a为根的次数最小的非零多项式；

(4) 如果 f ( x ) f(x) f(x)是域 F F F上任意一个以 a a a为根的多项式，则 p ( x ) ∣ f ( x ) p(x) \mid f(x) p(x)∣f(x)（即 p ( x ) p(x) p(x)整除 f ( x ) f(x) f(x)）。

定理 5.3.2

设 a a a是 F F F上的代数元， p ( x ) p(x) p(x)是 a a a在 F F F上的极小多项式， deg ⁡ ( p ( x ) ) = n \deg(p(x)) = n deg(p(x))=n，则

(1) F ( a ) = F [ a ] F(a) = F[a] F(a)=F[a]；

(2) F ( a ) F(a) F(a)是 F F F的有限扩张，且 [ F ( a ) : F ] = n [F(a): F] = n [F(a):F]=n；

(3) F ( a ) F(a) F(a)中的每一个元素都能唯一地表为
c 0 + c 1 a + c 2 a 2 + ⋯ + c n − 1 a n − 1 (5.3.1) c_0 + c_1a + c_2a^2 + \cdots + c_{n-1}a^{n-1} \tag{5.3.1} c0+c1a+c2a2+⋯+cn−1an−1(5.3.1)

的形式，其中 c 0 , c 1 , ⋯   , c n − 1 ∈ F c_0, c_1, \cdots, c_{n-1} \in F c0,c1,⋯,cn−1∈F。

推论 2 设 a 1 , a 2 , ⋯   , a s a_1,a_2,\cdots,a_s a1,a2,⋯,as都是 F F F上的代数元，则

(1) F ( a 1 , a 2 , ⋯   , a s ) = F [ a 1 , a 2 , ⋯   , a s ] F(a_1,a_2,\cdots,a_s) = F[a_1,a_2,\cdots,a_s] F(a1,a2,⋯,as)=F[a1,a2,⋯,as]；

(2) F ( a 1 , a 2 , ⋯   , a s ) F(a_1,a_2,\cdots,a_s) F(a1,a2,⋯,as)是 F F F的有限扩张，且

F ( a 1 , a 2 , ⋯   , a s ) : F \] ⩽ \[ F ( a 1 ) : F \] \[ F ( a 2 ) : F \] ⋯ \[ F ( a s ) : F \] . \[F(a_1,a_2,\\cdots,a_s): F\] \\leqslant \[F(a_1): F\]\[F(a_2): F\]\\cdots\[F(a_s): F\]. \[F(a1,a2,⋯,as):F\]⩽\[F(a1):F\]\[F(a2):F\]⋯\[F(as):F\]. **定理** :5.3.3 如果 E E E是 F F F的有限扩域，那么 E E E是 F F F的**代数扩张**。 **推论3** 设 a , a 1 , a 2 , ⋯   , a s a,a_1,a_2,\\cdots,a_s a,a1,a2,⋯,as都是 F F F上的代数元，则 F ( a ) F(a) F(a)与 F ( a 1 , a 2 , ⋯   , a s ) F(a_1,a_2,\\cdots,a_s) F(a1,a2,⋯,as)都是 F F F上的代数扩张。 **推论4** 设 a , b a,b a,b是 F F F上的代数元，那么 a + b a+b a+b、 a − b a-b a−b、 a ⋅ b a \\cdot b a⋅b以及 a b ( b ≠ 0 ) \\frac{a}{b}(b \\neq 0) ba(b=0)都是 F F F上的代数元。 **定理** :5.3.4 设 K K K是 E E E的代数扩张， E E E是 F F F的代数扩张，则 K K K是 F F F的代数扩张。 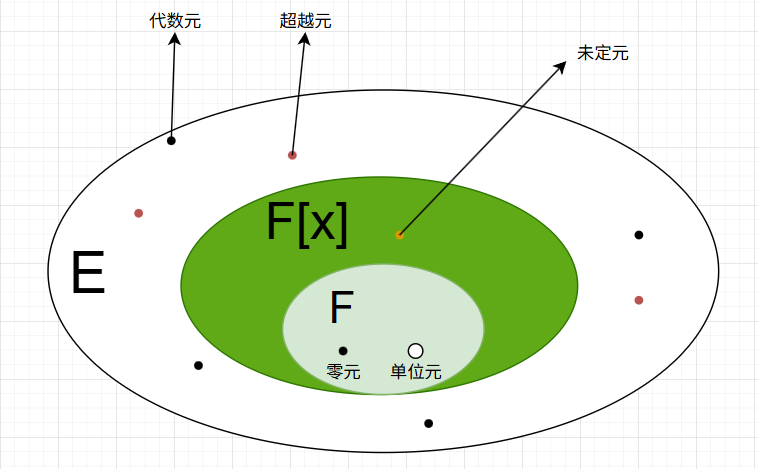 未定元：纯粹是"形式符号"，用于定义多项式环。 代数元/超越元：是真实存在于某个扩域中的元素，按是否满足代数方程来分类。 可以说：未定元是"理想化的超越元"，它保证了多项式环的自由性；而在具体扩域中，元素要么是代数元，要么是超越元。 **层次关系** ：结合**定理** :5.3.1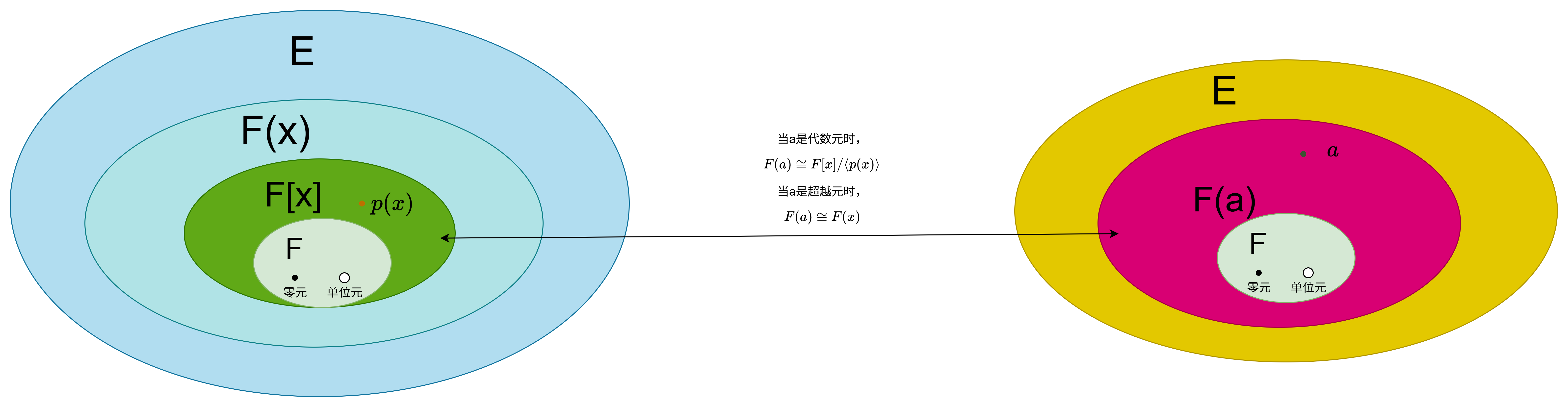 **扩张理解**： F ( a ) F(a) F(a) 是"数值化"的扩张：我们关心的是元素 a a a的具体数值性质 F \[ x \] F\[x\] F\[x\] 是"形式化"的扩张：我们关心的是多项式作为代数表达式的形式性质  ### 5.4多项式的分裂域 **定义**:分裂域 设 E E E是 F F F的扩域， f ( x ) f(x) f(x)为 F F F上的一个非常数多项式。如果 f ( x ) f(x) f(x)能分解成 E \[ x \] E\[x\] E\[x\]中一次因式的乘积，则称 f ( x ) f(x) f(x)在 E E E上是分裂的。如果 f ( x ) f(x) f(x)在 E E E上是分裂的，但 f ( x ) f(x) f(x)在 E E E的任一包含 F F F的真子域上都不分裂，则称\*\* E E E为多项式 f ( x ) f(x) f(x)在 F F F上的分裂域 (splitting field)。\*\* 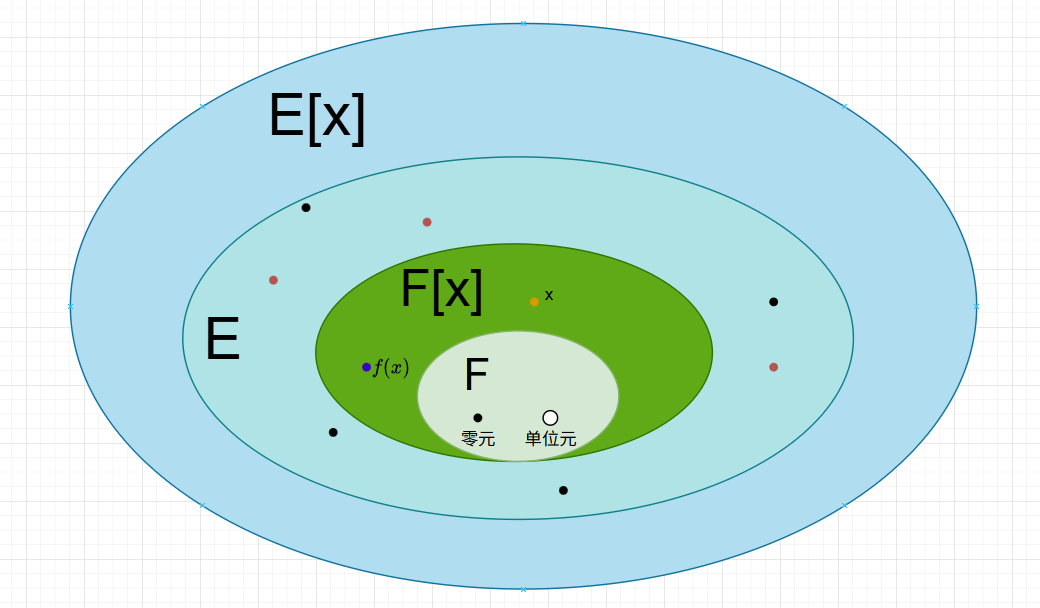 **定理** 5.4.1 设 f ( x ) ∈ F \[ x \] f(x) \\in F\[x\] f(x)∈F\[x\]， E E E是 F F F的扩域，且在 E E E上有 f ( x ) = b ( x − a 1 ) ( x − a 2 ) ⋯ ( x − a n ) , b ≠ 0 , f(x) = b(x - a_1)(x - a_2)\\cdots(x - a_n),\\ b \\neq 0, f(x)=b(x−a1)(x−a2)⋯(x−an), b=0, 则 E E E为 f ( x ) f(x) f(x)在 F F F上的分裂域的**充分必要** 条件是 E = F ( a 1 , a 2 , ⋯   , a n ) . E = F(a_1, a_2, \\cdots, a_n). E=F(a1,a2,⋯,an). **理解** ： 分裂域就是包含 F F F 和 f ( x ) f(x) f(x) 所有根的最小的域。如果 E E E比这个生成的域大，那就不是"最小"的，因此不是分裂域；如果 E E E小，可能缺一些根，所以也不满足。换句话说，分裂域就是"刚好"包含所有根的那个域。 **定理** 5.4.2 设 f ( x ) f(x) f(x)为域 F F F上的一个非常数多项式，则存在 F F F的扩域 E E E，使 E E E为 f ( x ) f(x) f(x)在 F F F上的分裂域。 **理解**：无论多项式多么复杂，我们总能找到一个"更大的"域（例如，通过逐步添加根来构造），在这个域中，多项式能完全分解成一次因式。这保证了分裂域总是存在的 **引理** 1 设 F F F是域， p ( x ) p(x) p(x)是 F F F上的一个不可约多项式， a a a是 p ( x ) p(x) p(x)在 F F F的某个扩域中的根。如果 ϕ \\phi ϕ是从 F F F到域 F ′ F' F′的域同构， b b b是 ϕ ( p ( x ) ) \\phi(p(x)) ϕ(p(x))在 F ′ F' F′的某个扩域中的根，那么存在 F ( a ) F(a) F(a)到 F ′ ( b ) F'(b) F′(b)的同构(假设为 ψ \\psi ψ)，它在 F F F上与 ϕ \\phi ϕ相同，且将 a a a映到 b b b。 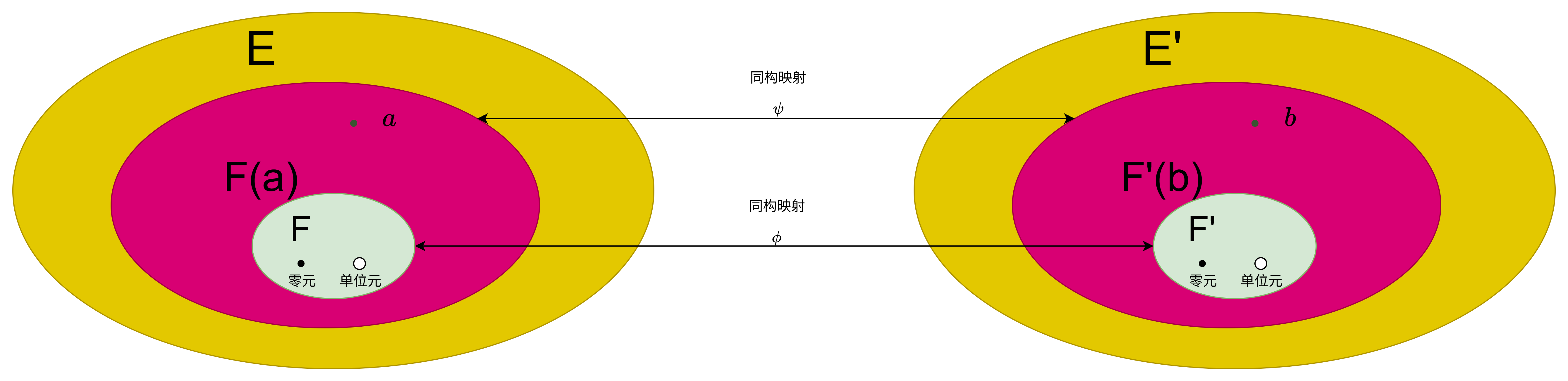 **推论** 1 设 F F F是域， p ( x ) p(x) p(x)是 F F F上的不可约多项式。如果 a a a是 p ( x ) p(x) p(x)在 F F F的某个扩域中的根， b b b是 p ( x ) p(x) p(x)在 F F F的另一个扩域中的根，那么域 F ( a ) F(a) F(a)与 F ( b ) F(b) F(b)同构。 （下面证明分裂域的同构唯一性。） **定理** 5.4.3 设 ϕ \\phi ϕ是域 F F F到 F ′ F' F′的同构， f ( x ) f(x) f(x)是 F F F上的非常数多项式。如果 E E E是 f ( x ) f(x) f(x)在 F F F上的分裂域， E ′ E' E′是 ϕ ( f ( x ) ) \\phi(f(x)) ϕ(f(x))在 F ′ F' F′上的分裂域，那么存在从 E E E到 E ′ E' E′的同构，且该同构在 F F F上与 ϕ \\phi ϕ一致。 **推论**2 设 F F F是域， f ( x ) ∈ F \[ x \] f(x) \\in F\[x\] f(x)∈F\[x\]，那么 f ( x ) f(x) f(x)在 F F F上的任何两个分裂域都是同构的。 **定义** 5.4.2 设 f ( x ) = a n x n + a n − 1 x n − 1 + ⋯ + a 1 x + a 0 ∈ F \[ x \] f(x) = a_nx\^n + a_{n-1}x\^{n-1} + \\cdots + a_1x + a_0 \\in F\[x\] f(x)=anxn+an−1xn−1+⋯+a1x+a0∈F\[x\]。称多项式 n a n x n − 1 + ( n − 1 ) a n − 1 x n − 2 + ⋯ + a 1 ∈ F \[ x \] na_nx\^{n-1} + (n-1)a_{n-1}x\^{n-2} + \\cdots + a_1 \\in F\[x\] nanxn−1+(n−1)an−1xn−2+⋯+a1∈F\[x

为 f ( x ) f(x) f(x)的导数 (derivative)，记作 f ′ ( x ) f'(x) f′(x)。

定理 5.4.4

设 f ( x ) , g ( x ) ∈ F [ x ] f(x), g(x) \in F[x] f(x),g(x)∈F[x]， a ∈ F a \in F a∈F，则

(1) ( f ( x ) + g ( x ) ) ′ = f ′ ( x ) + g ′ ( x ) (f(x) + g(x))' = f'(x) + g'(x) (f(x)+g(x))′=f′(x)+g′(x)；

(2) ( a f ( x ) ) ′ = a f ′ ( x ) (af(x))' = af'(x) (af(x))′=af′(x)；

(3) ( f ( x ) g ( x ) ) ′ = f ′ ( x ) g ( x ) + f ( x ) g ′ ( x ) (f(x)g(x))' = f'(x)g(x) + f(x)g'(x) (f(x)g(x))′=f′(x)g(x)+f(x)g′(x)。

定理 5.4.5

域 F F F上的多项式 f ( x ) f(x) f(x)在 F F F的某个扩域 E E E上有重根 的充要条件是 f ( x ) f(x) f(x)和 f ′ ( x ) f'(x) f′(x)在 F [ x ] F[x] F[x]中有正次数的公因式。

定理 5.4.6

设 f ( x ) f(x) f(x)是域 F F F上的不可约多项式。如果 F F F的特征为 0 0 0，那么 f ( x ) f(x) f(x)没有重根。如果 F F F的特征为 p ≠ 0 p \neq 0 p=0，那么仅当存在 F F F上的某个多项式 g ( x ) g(x) g(x)，使得 f ( x ) = g ( x p ) f(x) = g(x^p) f(x)=g(xp)时 f ( x ) f(x) f(x)有重根。

定义 5.4.3

如果域 F F F的特征为 0 0 0，或 F F F的特征为 p p p且 F p = { a p ∣ a ∈ F } = F F^p = \{a^p \mid a \in F\} = F Fp={ap∣a∈F}=F，则称 F F F为完备域(perfect field)。

定理 5.4.7

每个有限域都是完备域。

定理 5.4.8

如果 f ( x ) f(x) f(x)是完备域上的不可约多项式，那么 f ( x ) f(x) f(x)没有重根。

定理 5.4.9

设 f ( x ) f(x) f(x)是域 F F F上的不可约多项式， E E E是 f ( x ) f(x) f(x)在 F F F上的分裂域，那么 f ( x ) f(x) f(x)在 E E E中的所有根都有相同的重数。

推论 3

设 f ( x ) f(x) f(x)是域 F F F上的不可约多项式， E E E是 f ( x ) f(x) f(x)的分裂域，那么 f ( x ) f(x) f(x)可分解成如下形式：
a ( x − a 1 ) n ( x − a 2 ) n ⋯ ( x − a t ) n , a(x - a_1)^n(x - a_2)^n\cdots(x - a_t)^n, a(x−a1)n(x−a2)n⋯(x−at)n,

其中 a ∈ F a \in F a∈F， a 1 , a 2 , ⋯   , a t a_1, a_2, \cdots, a_t a1,a2,⋯,at是 E E E中不同的元素。

定理 5.4.10（施泰尼茨 (Steinitz), 1910）

设 F F F是特征为 0 0 0的域， a , b a, b a,b是 F F F上的代数元，则存在 c ∈ F ( a , b ) c \in F(a, b) c∈F(a,b)，使得 F ( a , b ) = F ( c ) F(a, b) = F(c) F(a,b)=F(c)。

推论 4

特征 0 0 0的域的任何有限扩域都是单扩域 。一个具有性质 E = F ( a ) E = F(a) E=F(a)的元素 a a a称为 E E E的本原元。

5.5有限域

本节要介绍抽象代数中最优美，也是非常重要的内容------有限域。有限域最早是由伽罗瓦在1830年证明一般五次方程不可解时引入的。到今天，有限域上的矩阵群已经成为一类重要的有限群（见习题5 - 1的20题和21题）。在过去的50年中，有限域在计算机科学、编码理论、信息论以及密码学中都有重要的应用。首先来考虑有限域的元素个数。

定义 ：有限域

一个具有有限个元素的域
性质：

加法群是阿贝尔群，乘法群是循环群的域是有限域

定理：5.5.1

有限域的阶是一个素数的幂

定理: 5.5.2

对每个素数 p p p 和每个正整数 n n n，在同构的意义下存在唯一的 p n p^n pn 阶的有限域，并且所有元素都是方程 x p n − x = 0 x^{p^n} - x = 0 xpn−x=0的根，该域的特征 为 p p p。

注：

因为对每个素数幂 p n p^n pn 仅存在一个 p n p^n pn 阶的域，所以可将此域记作 GF ( p n ) \text{GF}(p^n) GF(pn)（以纪念伽罗瓦），并称之为 p n p^n pn 阶的伽罗瓦域。 下面来讨论 p n p^n pn 阶域的结构。

**定理：**5.5.3

(1) GF ( p n ) \text{GF}(p^n) GF(pn) 作为加法群同构于
Z p ⊕ Z p ⊕ ⋯ ⊕ Z p ⏟ n 个 ; \underbrace{\mathbb{Z}_p \oplus \mathbb{Z}_p \oplus \cdots \oplus \mathbb{Z}p}{n个}; n个 Zp⊕Zp⊕⋯⊕Zp;

(2) GF ( p n ) \text{GF}(p^n) GF(pn) 的全体非零元的集合关于乘法构成的群是一个 p n − 1 p^n - 1 pn−1 阶的循环群。

推论 1

有限域 E E E是它的素子域的一个单扩域。

推论 2

GF ( p n ) : GF ( p ) \] = n . \[\\text{GF}(p\^n): \\text{GF}(p)\] = n. \[GF(pn):GF(p)\]=n. **推论** 3 设 a a a是 GF ( p n ) \\text{GF}(p\^n) GF(pn)的非零元乘法群的生成元，则 a a a 是 GF ( p ) \\text{GF}(p) GF(p)上的 n n n 次代数元。 **定理** :5.5.4 对于 n n n 的每个正因数 m m m，有限域 GF ( p n ) \\text{GF}(p\^n) GF(pn) 中存在唯一的 p m p\^m pm 阶子域，并且这些子域是 GF ( p n ) \\text{GF}(p\^n) GF(pn)中仅有的子域。 **有限域的构造** ： 有限域的构造是通过以下步骤实现的： 1. 从素数域 F p \\mathbb{F}_p Fp 开始 2. 在素数域 F p \\mathbb{F}_p Fp选择n次数的不可约多项式 f ( x ) f(x) f(x)（注：对于域 F \\mathbb{F} F上的多项式环 F \[ x \] \\mathbb{F}\[x\] F\[x\]，理想\< f ( x ) f(x) f(x)\>是**极大理想** 当且仅当 f ( x ) f(x) f(x)是**不可约多项式**） 3. 构造多项式环的商环 F p / ( f ( x ) ) \\mathbb{F}_p/(f(x)) Fp/(f(x))（注：结合上面注释，根据**环论基本定理** 可得 F p / ( f ( x ) ) \\mathbb{F}_p/(f(x)) Fp/(f(x))是域） 4. 得到的商环就是有限域 F p n \\mathbb{F}_{p\^n} Fpn （注： F p \[ x \] \\mathbb{F}_p\[x\] Fp\[x\] 中多项式的系数来自 F p \\mathbb{F}_p Fp，有 p p p 种选择，在商环 F p \[ x \] / ⟨ f ( x ) ⟩ \\mathbb{F}_p\[x\]/\\langle f(x) \\rangle Fp\[x\]/⟨f(x)⟩ 中，每个等价类可以由唯一的次数小于 n n n 的多项式代表。这样的多项式形如： a 0 + a 1 x + ⋯ + a n − 1 x n − 1 a_0 + a_1x + \\cdots + a_{n-1}x\^{n-1} a0+a1x+⋯+an−1xn−1，其中 a i ∈ F p a_i \\in \\mathbb{F}_p ai∈Fp，每个系数有 p p p 种选择，所以总共有： p × p × ⋯ × p = p n p \\times p \\times \\cdots \\times p = p\^n p×p×⋯×p=pn个元素） F p n = F p \[ x \] / ⟨ f ( x ) ⟩ \\mathbb{F}_{p\^n} = \\mathbb{F}_p\[x\]/\\langle f(x) \\rangle Fpn=Fp\[x\]/⟨f(x)⟩ 其中 f ( x ) f(x) f(x) 是 F p \\mathbb{F}_p Fp 上的 n n n 次不可约多项式。 例子：从 F 2 \\mathbb{F}_2 F2 构造 F 256 \\mathbb{F}_{256} F256 1. **基础域** ：从素数域 F 2 = { 0 , 1 } \\mathbb{F}_2 = \\{0,1\\} F2={0,1} 开始 2. **选择不可约多项式** ：在 F 2 \[ x \] \\mathbb{F}_2\[x\] F2\[x\] 中选择一个8次不可约多项式 f ( x ) f(x) f(x) * 例如： f ( x ) = x 8 + x 4 + x 3 + x + 1 f(x) = x\^8 + x\^4 + x\^3 + x + 1 f(x)=x8+x4+x3+x+1 3. **构造商环** ： F 256 = F 2 \[ x \] / ⟨ f ( x ) ⟩ \\mathbb{F}_{256} = \\mathbb{F}_2\[x\]/\\langle f(x) \\rangle F256=F2\[x\]/⟨f(x)⟩ 4. **域元素表示** ： F 256 \\mathbb{F}_{256} F256 中的每个元素可以表示为： a 0 + a 1 x + a 2 x 2 + ⋯ + a 7 x 7 a_0 + a_1x + a_2x\^2 + \\cdots + a_7x\^7 a0+a1x+a2x2+⋯+a7x7 其中 a i ∈ F 2 = { 0 , 1 } a_i \\in \\mathbb{F}_2 = \\{0,1\\} ai∈F2={0,1}，共有 2 8 = 256 2\^8 = 256 28=256 个元素 F 256 \\mathbb{F}_{256} F256 运算： * 加法运算 多项式系数在 F 2 \\mathbb{F}_2 F2 中按位相加（模2加法）等价于按位异或(XOR)运算 例如： ( x 3 + x + 1 ) + ( x 2 + x ) = x 3 + x 2 + 1 (x\^3 + x + 1) + (x\^2 + x) = x\^3 + x\^2 + 1 (x3+x+1)+(x2+x)=x3+x2+1 * 乘法运算 1. 先进行普通多项式乘法 2. 结果对不可约多项式 f ( x ) f(x) f(x) 取模（在 F 2 \\mathbb{F}_2 F2 系数下） 3. 保证结果仍是次数小于8的多项式 例如：计算 x 4 ⋅ x 3 = x 7 x\^4 \\cdot x\^3 = x\^7 x4⋅x3=x7（未超过8次，直接得结果） 计算 x 7 ⋅ x = x 8 x\^7 \\cdot x = x\^8 x7⋅x=x8，由于 x 8 ≡ x 4 + x 3 + x + 1 ( m o d f ( x ) ) x\^8 \\equiv x\^4 + x\^3 + x + 1 \\pmod{f(x)} x8≡x4+x3+x+1(modf(x))，所以结果为 x 4 + x 3 + x + 1 x\^4 + x\^3 + x + 1 x4+x3+x+1 参考： [近世代数 \| 韩士安, 林磊 \| download on Z-Library](https://z-lib.by/book/18151929/fad168/%E8%BF%91%E4%B8%96%E4%BB%A3%E6%95%B0.html)近世代数 ------韩士安 [代数结构入门：群、环、域、向量空间 - 知乎](https://zhuanlan.zhihu.com/p/21583674) [【静夜思】一些抽象代数的核心思想和实际应用_抽象代数有什么用-CSDN博客](https://blog.csdn.net/hanss2/article/details/99173432)