以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。

分析:
题目给了若干个区间,每个区间都有一个开始位置和一个结束位置,题目要我们把所有有重叠的区间合并,最后得到一组互不重叠、但能完整覆盖原区间的结果。如果区间是乱序的,我们根本没法判断当前区间应该和哪个区间合并,因为可能后面还有一个起点更小的区间。所以第一步先把所有区间按开始位置从小到大排好顺序,方便后面的操作。
排序完成之后,观察一下区间在什么情况下会出现重合。
以intervals = [[1,3],[2,6],[8,10],[15,18]]为例
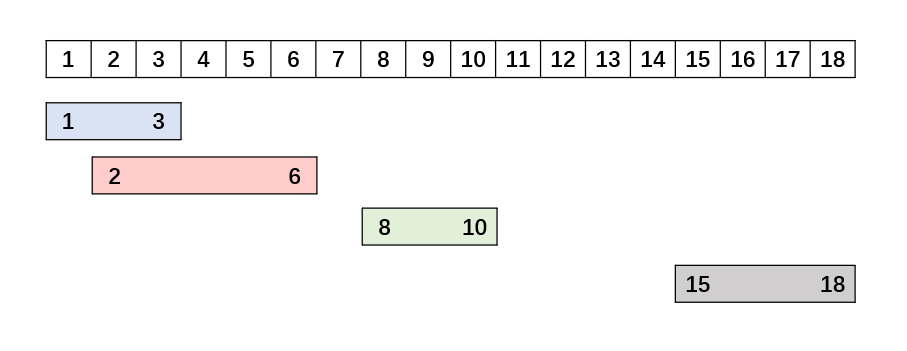
图上可以看得蓝色的[1,3]和粉色的[2,6]重合了,可以发现判断重合最重要的就是前面一组数的end和后面一组数的start进行比较,也就是蓝色的3和粉色的2进行比较,如果第二组数的stat<=第一组数的end,那么就可以进行合并。例子中粉2<=蓝3,就可以进行合并。因为一开始已经进行过排序了,所以这时候只需要前后二组两两比较就可以了。
合并后变成了这样:
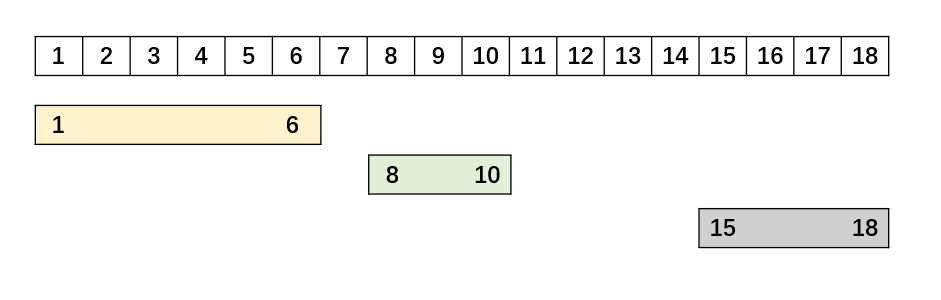
前面已经分析了合并条件,现在考虑如果需要合并,那么合并后的那个区间start和end的值是什么。
start的值只需要沿用前面的区间的start就可以,因为因为排序已经保证当前合并区间的start位置一定是这两个区间中最靠左的那个。真正需要更新的是end位置,它应该延伸到两个区间中能到达的最远位置,所以只需要取两个区间的end值的max就好了。比如这里合并前的[1,3]中的3和[2,6]中的6比较,6是更大的,那么就选6作为新的end,最终合并成黄色的那块区间[1,6]。
可以用res来存放合并后的结果。一开始先选第一个区间[1,3]作为当前合并区间,因为它前面没有任何区间,不可能发生合并问题,所以这个区间可以在最初就直接放到res中去。然后开始看后面的区间。当我们走到一个新的区间时,只需要关心一件事:它的开始位置,是否落在当前合并区间的范围之内。如果新的区间开始的位置小于等于当前区间结束的位置,说明在当前区间还没结束的时候,新区间就已经开始了,这两个区间在数轴上是连在一起的,因此它们必须被合并。此刻我们看[2,6],与res中的最后一组数[1,3]进行比较,发现满足条件。满足条件合并后的区间,start不需要重新计算,只需要去更新end,此时res中变成了[1,6]。但是如果新的区间start大于当前区间end,说明这两个区间在数轴上是完全分开的,中间没有任何重叠部分。这种情况下,只需要把它固定下来,加入到res中,然后把新的区间当作一个全新的合并区间,继续向后比较。比如这里再往后看[8,10],这里[8,10]中的start 8>[1,6]中的end 6,所以可以确定是无重叠的,直接把[8,10]加入到res中就可以这时res中就变成了[[1,6], [8,10]]。按照这个规则一路向后扫描,每一步要么扩展当前区间的结束位置,要么开启一个新的区间直接存到res。由于区间已经排好序,任何区间只可能和它左边最近的那个区间发生重叠,永远不需要回头看更早的区间。当所有区间都扫描完成后,所有合并好的区间自然就形成了一组互不重叠、并且完整覆盖原区间的结果。
C++代码如下:
cpp
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
if (intervals.empty()) {
return {};
}
sort(intervals.begin(), intervals.end());// 排序
vector<vector<int>> res;
res.push_back(intervals[0]);// 第一组数先存到res中
for (int i = 1; i < intervals.size();i++) {
if (intervals[i][0]<= res.back()[1]){// 有重叠,进行处理,更新res中最后一组数的end值
res.back()[1] = max(intervals[i][1],res.back()[1]);
}
else {
res.push_back(intervals[i]);// 无重叠,直接加入
}
}
return res;
}
};