【iOS】简单的四则运算
前言
四则运算的本质是使用运算符号优先级来判断是否入栈出栈,其思路有两种:一种是中缀表达式转后缀表达式,对后缀表达式进行计算得到结果;另一种是直接使用中缀表达式计算结果。
表达式
- 中缀表达式:操作符以中缀形式位于运算数中间,是我们日常通用的算术逻辑公式,如 3 + 2。
- 后缀表达式:又称逆波兰式,操作符以后缀形式位于两个运算数后,如 3 2 +。
- 前缀表达式:又称波兰式,操作符以前缀形式位于两个运算数前,如 + 3 2。
其中中缀表达式适合于人类思维结构和运算习惯,但不适用于计算机。适用于计算机的表达式是后缀表达式。与中缀表达式不同,后缀表达式不需要使用括号来标识操作符的优先级,而是按操作符从左到右出现的顺序依次执行进行计算。
进行简单四则运算
无论哪种方法计算,都需要使用栈,因此我们要使用OC数组等模拟实现栈:
objc
#import <Foundation/Foundation.h>
@interface Stack : NSObject
@property(nonatomic, strong) NSMutableArray *stackArray;
@property(nonatomic, assign) NSInteger stackSize;
-(void)push:(double)num;
-(void)pop:(double*)num;
-(double)getTop;
-(BOOL)isEmpty;
@end
objc
#import "Stack.h"
@implementation Stack
-(instancetype)init {
self = [super init];
if (self) {
//+arrayWithCapacity:(NSUInteger)numItems:创建可变数组
self.stackArray = [NSMutableArray arrayWithCapacity:100];
self.stackSize = 100;
}
return self;
}
-(void)push:(double)num {
[self.stackArray addObject:@(num)];
}
-(void)pop:(double *)num {
if (self.stackArray.count > 0) {
NSNumber *last = [self.stackArray lastObject];
*num = [last doubleValue];
[self.stackArray removeLastObject];
}
}
-(double)getTop {
return [[self.stackArray lastObject] doubleValue];
}
-(BOOL)isEmpty {
return self.stackArray.count == 0;
}
@end直接使用中缀表达式计算
直接使用中缀表达式计算不需要生成一个新的表达式序列,而是使用两个栈一边读取一边计算,动态判断是否直接计算或者先压入栈。
这里我们提前写好运算符优先级表,行对应 theta1(栈顶运算符),列对应 theta2(当前读入的运算符)。
其返回值:
- '<':栈顶运算符优先级低,当前读入运算符入栈
- '>':栈顶运算符优先级高,栈顶符号出栈并计算
- '=':括号匹配或表达式结束
- '0':非法情况
| i\j | + | - | ***** | / | ( | ) | = |
|---|---|---|---|---|---|---|---|
| + | > | > | < | < | < | > | > |
| - | > | > | < | < | < | > | > |
| ***** | > | > | > | > | < | > | > |
| / | > | > | > | > | < | > | > |
| ( | < | < | < | < | < | = | 0 |
| ) | > | > | > | > | 0 | > | > |
| = | < | < | < | < | < | 0 | = |
具体实现:
objc
char Precede(char theta1, char theta2) {
//theta1:栈顶运算符
//theta2:当前正在处理运算符
int i = 0, j = 0;
char pre[7][7] = {
{'>', '>', '<', '<', '<', '>', '>'},
{'>', '>', '<', '<', '<', '>', '>'},
{'>', '>', '>', '>', '<', '>', '>'},
{'>', '>', '>', '>', '<', '>', '>'},
{'<', '<', '<', '<', '<', '=', '0'},
{'>', '>', '>', '>', '0', '>', '>'},
{'<', '<', '<', '<', '<', '0', '='}
};
switch (theta1) {
case '+':
i = 0;
break;
case '-':
i = 1;
break;
case '*':
i = 2;
break;
case '/':
i = 3;
break;
case '(':
i = 4;
break;
case ')':
i = 5;
break;
case '=':
i = 6;
break;
}
switch (theta2) {
case '+':
j = 0;
break;
case '-':
j = 1;
break;
case '*':
j = 2;
break;
case '/':
j = 3;
break;
case '(':
j = 4;
break;
case ')':
j = 5;
break;
case '=':
j = 6;
break;
}
return pre[i][j];
}后续的主要逻辑是,初始化两个栈,一个存储数字,一个存储运算符号,然后将符号与数字不断地入栈出栈知道"="。其中对小数、负数再单独进行处理。
这里展示主要运算操作部分:
objc
-(NSString *)evaluateResult:(NSString *)input {
int index = 0;
int isNegative = 0;
int isParentheses = 0;
self.StackNum = [[Model alloc] init];
self.StackSign = [[Model alloc] init];
[self.StackSign push:'='];
char ch = [input characterAtIndex:index++];
if (ch == '-') {
ch = [input characterAtIndex:index++];
isNegative = 1;
}
double a, b, theta, x1, x2;
while (ch != '=' || [self.StackSign getTop] != '=') {
if (istTheta(ch)) {
if (ch == '(') {
isParentheses = 1;
}
if (ch == '-' && [input characterAtIndex:index - 2] == '(') {
//检查符号前是否有括号判断是否为负数
//检查后重置isParentheses,防止让程序以为自己还在括号开头
isNegative = 1;
isParentheses = 0;
ch = [input characterAtIndex:index++];
continue;//判断为符号而不是运算符减,跳出while循环剩余部分,避免继续往下执行将-当作减号运算符压入符号栈
}
switch (Precede([self.StackSign getTop], ch)) {
case '<':
[self.StackSign push:ch];
ch = [input characterAtIndex:index++];
break;
case '>':
[self.StackSign pop:&theta];
[self.StackNum pop:&b];
[self.StackNum pop:&a];
[self.StackNum push:Operate(a, theta, b)];
break;
case '=':
[self.StackSign pop:&theta];
ch = [input characterAtIndex:index++];
break;
}
} else if (isdigit(ch)) {
x1 = ch - '0';
[self.StackNum push:x1];
x2 = x1;
ch = [input characterAtIndex:index++];
while (isdigit(ch)) {
x1 = ch - '0';
x2 = 10 * x2 + x1;
ch = [input characterAtIndex:index++];
}
if (ch == '.') {
ch = [input characterAtIndex:index++];
double decimal = 0.0;
double count = 0;
while (isdigit(ch)) {
double f = (double)(ch - '0');
decimal += f / pow(10, count++);
ch = [input characterAtIndex:index++];
x2 += decimal;
}
}
double tempX1;
[self.StackNum pop:&tempX1];
if (isNegative) {
[self.StackNum push:-x2];
} else {
[self.StackNum push:x2];
}
} else {
return @"错误";
}
}
double result = [self.StackNum getTop];
if (isnan(result)) {
return @"错误";
} else {
NSString *resultString = [NSString stringWithFormat:@"%f", result];
resultString = [self removeZero:resultString];
return resultString;
}
}输入几个算式验证下运算结果:

中缀表达式转后缀表达式再计算
中缀表达式转后缀表达式
主要操作为:准备一个字符栈存储尚未处理的操作符和括号,从左至右依次遍历中缀表达式各个字符。
- 字符为运算数:直接送入后缀表达式。
- 字符为左括号:直接入栈。
- 字符为右括号:直接出栈,并将出栈字符依次送入后缀表达式,直到栈顶字符为左括号,只要满足栈顶为左括号,即可进行最后一次出栈 。
(左右括号只出栈,不送入后缀表达式) - 字符为操作符:
- 若栈空:直接入栈。
- 若栈非空:判断栈顶操作符。若栈顶操作符低于该操作符,该操作符入栈;否则出栈,并将出栈字符依次送入后缀表达式,直到栈空或栈顶操作符优先级高于该操作符,停止出栈。
- 重复上述步骤直至完成中缀表达式的遍历,接着判断字符栈是否为空,非空直接出栈,并将出栈字符依次送入后缀表达式。
objc
-(NSArray*)infixToPostfix:(NSArray*)tokens {
NSMutableArray *output = [NSMutableArray array];
Model *model = [[Model alloc] init];
for (NSString *token in tokens) {
if (token.length == 0) {
continue;
}
if (![self isTheta:token]) {
[output addObject:token];
} else {
if ([token isEqualToString:@"("]) {
[model push:token];
} else if ([token isEqualToString:@")"]) {
while (![[model top] isEqualToString:@"("]) {
[output addObject:[model pop]];
}
[model pop];
} else {
while (![model isEmpty] && [self priorityOfOperator:[model top]] >= [self priorityOfOperator:token]) {
[output addObject:[model pop]];
}
[model push:token];
}
}
}
while (![model isEmpty]) {
[output addObject:[model pop]];
}
return output;
}这里可以参考《数据结构》:中缀表达式转后缀表达式 + 后缀表达式的计算博客中的示例图来更形象地理解。
后缀表达式的计算
主要操作为:准备一个运算数栈存储运算数和操作结果,从左至右依次遍历后缀表达式各个字符。
- 字符为运算数:直接入栈。
- 字符为操作符:连续出栈两次,使用出栈的两个数据进行相应计算,并将计算结果入栈。
(注意 :第一个出栈的运算数为 a ,第二个为 b ,此时的运算符为 - ,计算为 b - a ,a 和 b 顺序不能反!!)
- 重复上述步骤直完成后缀表达式的遍历,最后栈中的数据就是计算结果。
objc
-(double)evaluatePostfix:(NSArray*)tokens {
Model *model = [[Model alloc] init];
for (NSString *token in tokens) {
if (![self isTheta:token]) {
[model push:@(token.doubleValue)];
} else {
double a = [[model pop] doubleValue];
double b = [[model pop] doubleValue];
double result = 0;
if ([token isEqualToString:@"+"]) {
result = b + a;
} else if ([token isEqualToString:@"-"]) {
result = b - a;
} else if ([token isEqualToString:@"*"]) {
result = b * a;
} else if ([token isEqualToString:@"/"]) {
if (a == 0) {
return NAN;
}
result = b / a;
}
[model push:@(result)];
}
}
return [[model pop] doubleValue];
}这里值得注意的有两点:
- 分词
我们需要将每个运算符和数字分隔开各自作为一个字符存入数组中(尤其注意代码中分隔负数的方法)
objc
-(NSArray*)tokenize:(NSString*)input {
NSMutableArray *tokens = [NSMutableArray array];
NSMutableString *numberBuffer = [NSMutableString string];
for (int i = 0; i < input.length; i++) {
unichar ch = [input characterAtIndex:i];//当前字符
NSString *chStr = [NSString stringWithFormat:@"%c", ch];//字符改写成字符串形式
BOOL isNegative = NO;
if (ch == '-') {
if (i == 0) {
isNegative = YES;
} else {
unichar preChar = [input characterAtIndex:i - 1];
if ([self isTheta:[NSString stringWithFormat:@"%c", preChar]] && preChar != ')') {
isNegative = YES;
}
}
}
if (isdigit(ch) || ch == '.' || isNegative) {
//如果是数字、小数、负数,追加到字符后面形成完整数字
[numberBuffer appendString:chStr];
} else {
if (numberBuffer.length > 0) {
//将处理好的完整数字加到数组中并置空,准备处理下一个字符
//[tokens addObject:numberBuffer];
[tokens addObject:[numberBuffer copy]];
[numberBuffer setString:@""];
}
if (ch != ' ' && ch != '=') {
[tokens addObject:chStr];
}
}
}
if (numberBuffer.length > 0) {
//[tokens addObject:numberBuffer];
[tokens addObject:[numberBuffer copy]];
}
return tokens;
}- NSMutableString的可变性和对象引用
我们在分词时,有一个缓存字符串numberBuffer,当我们得到完整数字或是符号,并要将其加到数组tokens中时,使用了copy。
objc
[tokens addObject:[numberBuffer copy]];那么为什么不是直接把numberBuffer添加到tokens数组中呢?
回想一下copy的内容,非容器类可变对象的copy和mutableCopy都是深拷贝,与原对象不共用同一内存地址,也就是说[numberBuffer copy]会创建一个NSString副本,这样数组中每个元素不会随numberBuffer改变而改变。
这样的输出是正确的:

然而,[tokens addObject:numberBuffer]存的是同一个NSMutableString 的引用,当numberBuffer的值改变时,数组中对应内容也会随之改变,这样tokens中的数组最终都会变成最后一次numberBuffer的内容。
这样会违背我们的预期,输出结果就是错误的:

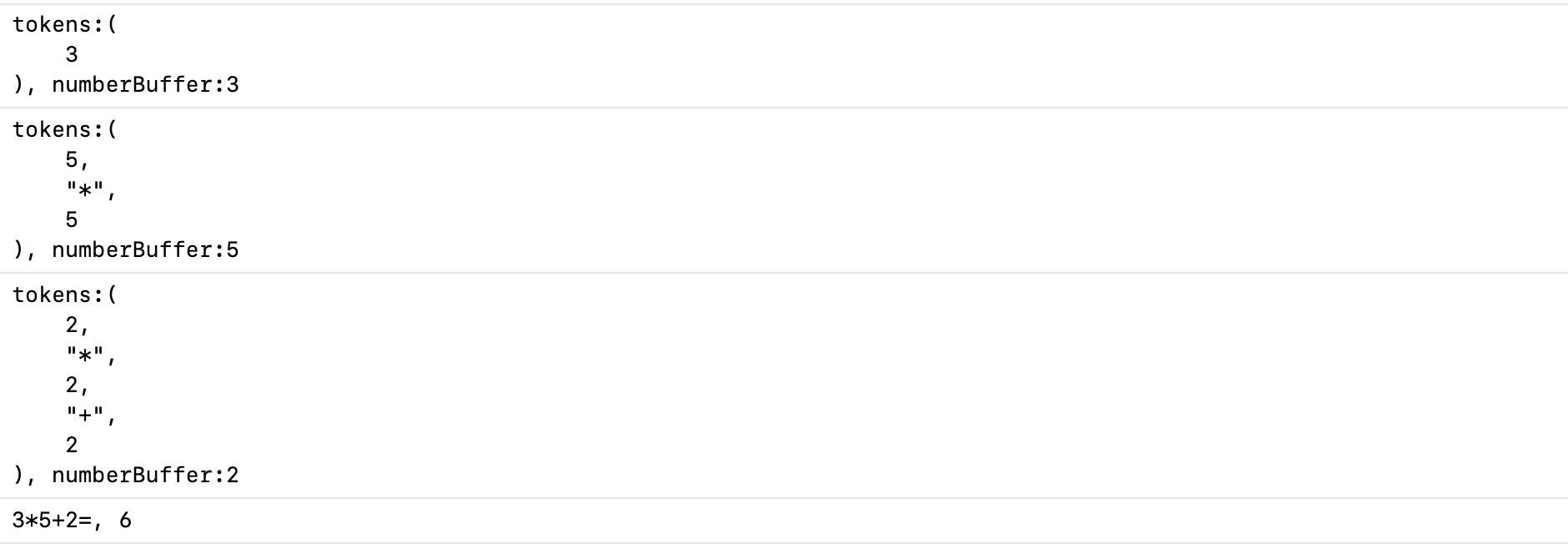
这里我们再逐步输出一下tokens和numberBuffer直观地看一下不使用copy的问题:
总结
简单的四则运算是我在仿写计算器时的核心,同时也对栈的学习很有帮助,后面将会多复习这里。