🎬 胖咕噜的稞达鸭 :个人主页
🔥 个人专栏 : 《数据结构》《C++初阶高阶》《算法入门》
⛺️技术的杠杆,撬动整个世界!

最小栈
题目解析 :
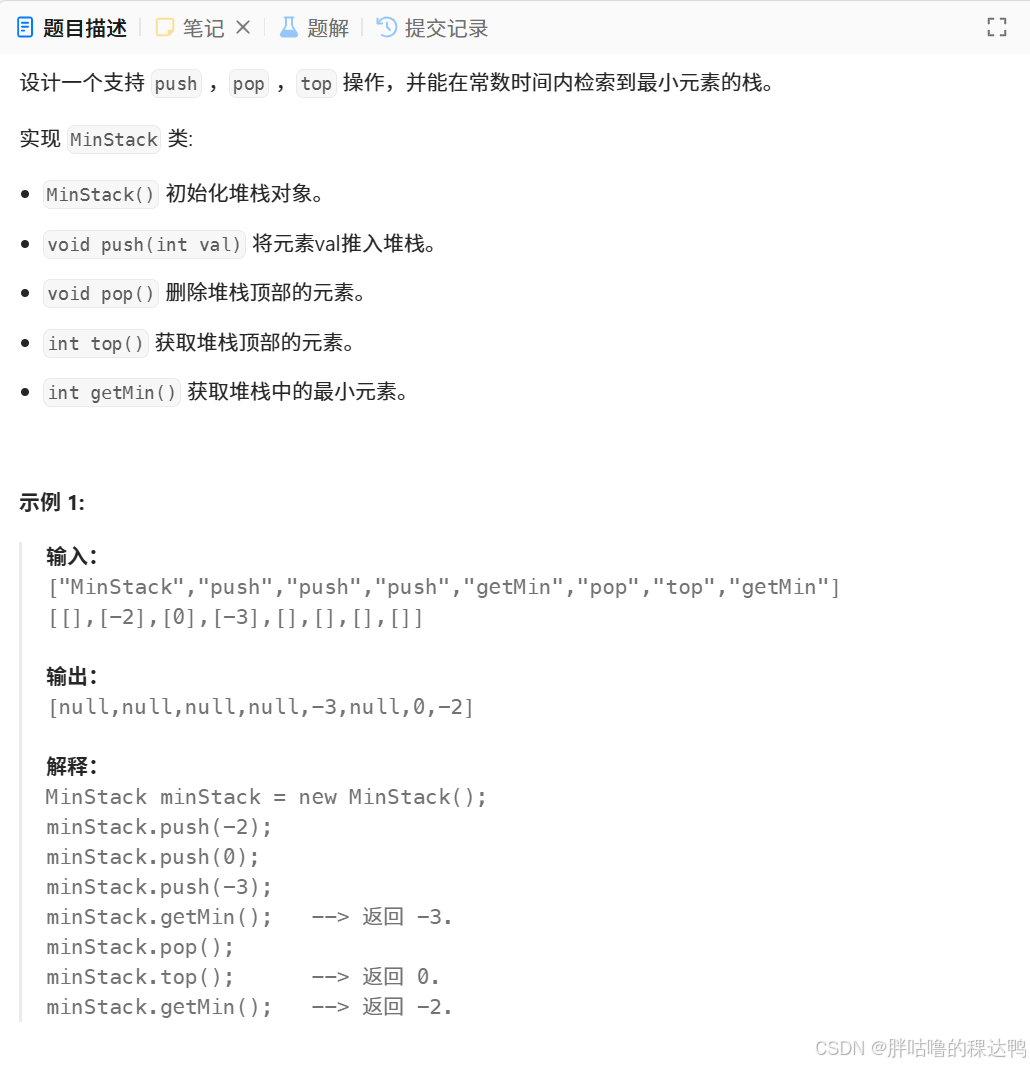
这个题目需要设计一个特殊的栈(被称为最小栈),它需要支持普通栈的push,pop,top等操作,同时还需要在常数时间(O(1))内找到栈中的最小元素,通过getMin()实现。
思路 :
题目中需要找出最小元素的栈,搞两个栈,一个定义_st,是正常的栈,一个辅助栈,叫_minst,假如第一个入栈的数据是5,入栈_st第一个数字是5,_minst也入栈5,后来入栈的数字都进入正常的栈_st内,只有比5小的数字才插入_minst中,假设3,入栈_st,比5小,同样入栈_minst,也就是说,入栈_minst的数只能是小于第一次入栈_minst的数字。
用辅助栈记住内阁数据栈状态下的最小值,那要是相等的呢?
答案是:要计入的,假如最后删除数字的时候,在_st中没有入栈_minst的都需要被删除。
下面就是如何将我们的思路过程转化为代码呈现在OJ题上。
定义两个栈,都是stack<int>类型的,普通栈stack<int>_st,辅助栈stack<int>_minst,构造栈可以不写,编译器对于内置类型会取自动调用默认生成的,自定义类型也会调用默认构造,在库里会提供,自动调用,析构也不用写。
直接开始进行插入,在_st中插入数据val,在_minst中插入数据的条件是要么_minst为空,要么即将插入的值小于等于入栈_minst的数字;
删除数字,对于_st来说,不管任何条件都需要删除,_minst中,删除的数字要满足等于_st栈顶的数字;
最后返回两个栈,getMin()将会返回最小元素,达到题目要求。
上代码!
cpp
class MinStack {
public:
MinStack() {
}
void push(int val) {
_st.push(val);
if(_minst.empty()||val<=_minst.top())
{
_minst.push(val);
}
}
void pop() {
if(_st.top()==_minst.top())
{
_minst.pop();
}
_st.pop();
}
int top() {
return _st.top();
}
int getMin() {
return _minst.top();
}
private:
stack<int>_st;
stack<int>_minst;
};栈的压入,弹出序列
栈的压入,弹出序列
题目解析:
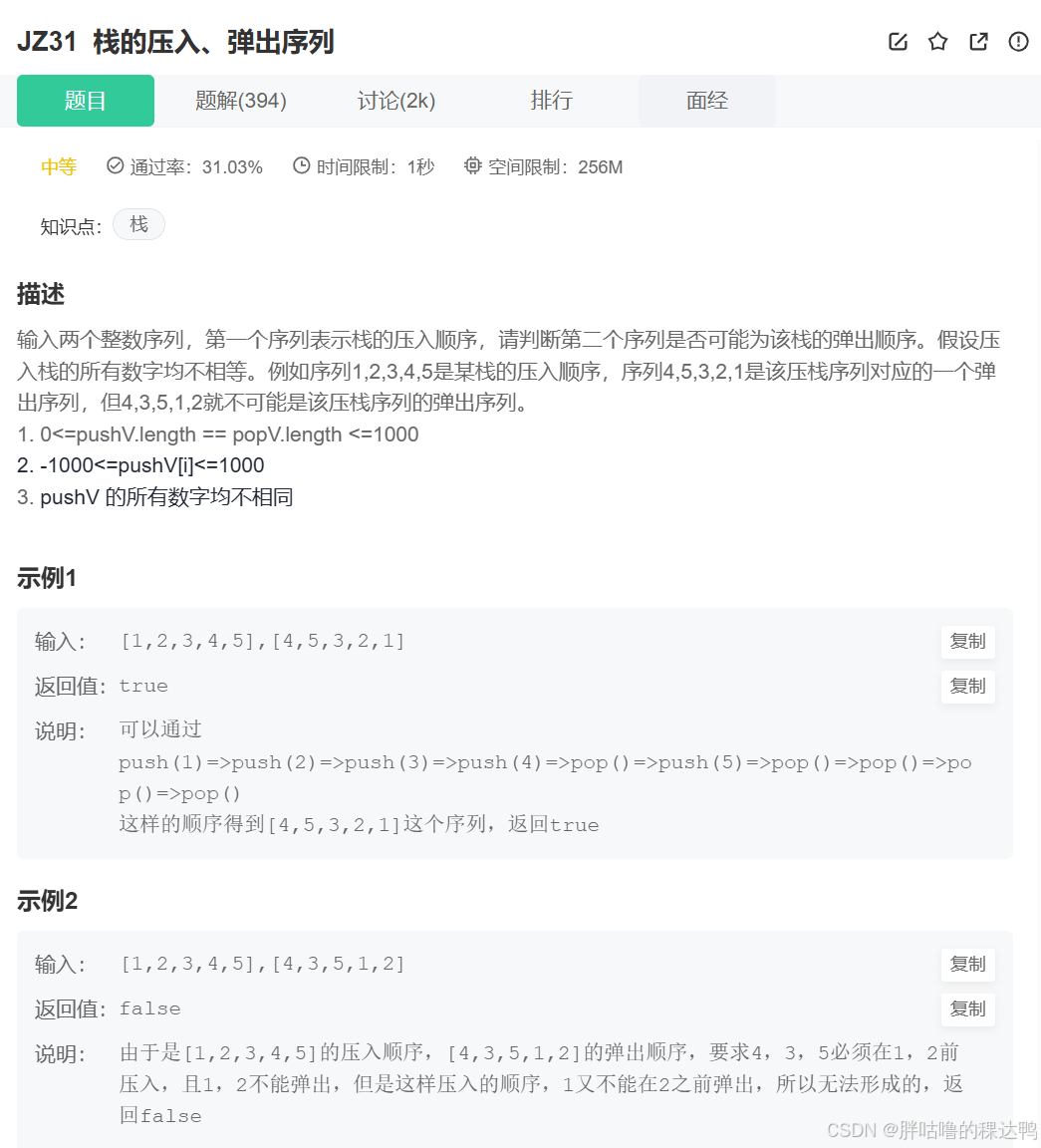
判断第二个整数序列是否是第一个整数序列(表示栈的压入顺序)对应的弹出顺序;通俗一点解释,栈的特点是"先进后出",比如往栈中压入1-2-3,弹出的顺序只能是3-2-1,第一个序列,压入顺序:1-2-3-4-5,第二个序列,需要判断的弹出顺序,随时压入,随时弹出。
这里我们用示例1来进行解释:
1.先入栈序列入栈一个值,
2.栈顶数据跟出栈序列是否匹配,匹配就持续出;
3.入栈序列结束,就结束了
对于入栈序列1-2-3-4-5,和出栈序列4-5-3-2-1;分别用指针指向两个序列的第一个值,入栈组1先入栈,跟出栈组4进行比对,不匹配,继续入栈;入栈组2,跟出栈组4比对,不匹配,继续入栈,入栈组3,跟出栈组4比对,不匹配,继续入栈,入栈组4,跟出栈组4比对,匹配,出栈;此时出栈组要指向下一个数字5;入栈组5,跟出栈组5比对,匹配,出栈;接着继续匹配,得出4-5-3-2-1是1-2-3-4-5的弹出顺序。
下面就是如何将我们的思路过程转化为代码呈现在OJ题上。
定义一个存储int类型的栈,利用"先进后出"的特性模拟入栈,出栈过程。
范围for循环遍历入栈序列pushV中的每一个元素,再将当前元素压入栈中st.push(e),接着要跟出栈序列进行比对,为了遍历出栈序列,我们定义一个无符号整数变量popi,作为出栈序列popV的索引指针,只要栈不为空!st.empty()而且栈顶元素等于出栈序列的当前索引popi位置的元素,就执行出栈操作,如果有元素出栈,popi往后挪动,继续判断下一个出栈元素;
当遍历完出栈序列后,判断栈是否为空, return st.empty();如果栈为空,那么说明所有栈中的元素在出栈序列中都有匹配的对象,如果栈不为空,那就说明当前的出栈序列不符合入栈序列的顺序。
cpp
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param pushV int整型vector
* @param popV int整型vector
* @return bool布尔型
*/
bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {
//首先需要遍历出栈序列
size_t popi=0;
stack<int>q;//两个序列定义一个栈
for(auto& e:pushV)//范围for遍历入栈序列pushV
{
q.push(e);//插入值
while(!q.empty() && q.top()==popV[popi])//栈顶元素等于出栈序列的当前索引`popi`位置的元素,并且栈不为空
{
q.pop();//就执行出栈操作
popi++;//出栈之后索引++
}
}
return q.empty();
}
};二叉树层序遍历
二叉树层序遍历
题目解析:
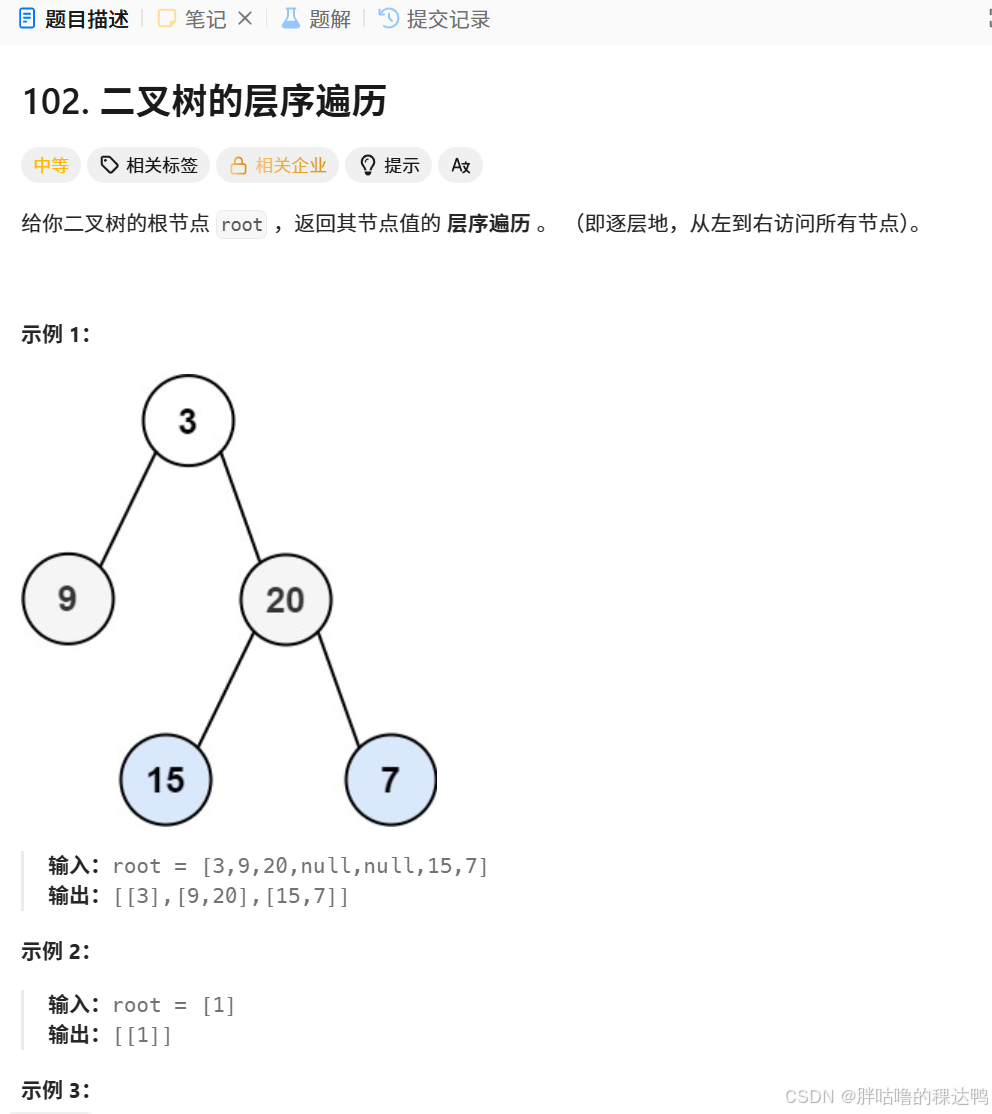
要求遍历二叉树,每一层都要放到一个二维数组当中,每一行的数据个数是不规则的,但是我们如何获取每一行的数据放到每一行呢?
思路:
思路一 :这里我们定义两个队列,用一个q1存储二叉树节点的元素,queue<TreeNode*>q1,一个q2用于存储当前节点是第几层的,queue<int>q2,当第一个根节点3入queue<TreeNode*>q1队列,在q2队列记录第一层;广度优先遍历,第二次入q1队列,需要拿到3的子节点,9和20,在q2队列计入2 2,作为第二层;依次直到记录完所有的二叉树节点,队列为空。
思路二 :
我们只用一个队列和重要变量levelsize,levelsize用来记录当前层的数据个数,这个思路的思想是一层一层出,第一层入数据3,levelsize统计为1,出数据用levelsize--表示;这时候3会顺带过来下一层数据9和20,levelsize统计为2,出数据用levelsize--表示;这时候9和20会带过来下一层的数据25,15和7,levelsize统计为3,出数据用levelsize--表示。最后将遍历到的数据插入二维数组中。
问题来了:
levelsize作为一个被定义的变量,如何获取到队列中的元素?
答:队列入数据出数据会带过来下一层数据,只要进入过的数据它们之后没有节点,都为空子树,就拿不到了,此时也大致完成了我们一层一层记录节点个数的过程。
综合下来我们选择第二种思路来写代码:
下面就是如何将我们的思路过程转化为代码呈现在OJ题上。
这道题目的最终目的是将二叉树中的节点按照每一层的数据一层一层拿下来,最后插入封装在二维数组中。所以我们首先需要一个二维数组,**vect<vect<int>>vv**;一个队列queue<TreeNode*>q;
接着就可以开始放数据,定义一个levelsize来记录当前层的数据个数,如果根节点不为空,就插入队列q 中,并且相应的levelsize多了一个数据,levelsize赋值1;
接着进行子节点的遍历提取计数,对于每一层的节点取出来之后都需要一个数组进行封装,所以vector<int>v定义用来储存每一层的节点,二叉树每一层的头节点作为队列每一层的头节点,TreeNode* front=q.front();在队列中删除进行这一层下一个节点的提取,q.pop();将头节点插入到数组中,v.push_back(front->val);
注意:这里不是删除了这个节点,队列中只有删除第一个,才可以拿到第二个,进行不断地提取,直到整个队列为空,这里我们用levelsize--,也就是每一层如果levelsize为0,就进行下一层的操作。
队列出数据入数据会将子节点带过来,分别判断如果front的左右子节点不为空,那么就入队列,执行while(!q.empty());队列不为空,循环执行以上操作。
最后队列为空,也就说明所有的二叉树节点每一层都在每一层对应的数组中做好了封装,这里我们来进行封装的汇总,vv.push_back(v);最后返回vv,结束作答。
上代码!
cpp
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>>vv;//定义一个二维数组用来存储最后的结果
queue<TreeNode*>q;
int levelsize=0;
if(root)
{
q.push(root);
levelsize=1;
}
while(!q.empty())
{
//当前层数据个数,控制一层一层出
vector<int>v;
while(levelsize--)
{
TreeNode* front=q.front();
q.pop();
v.push_back(front->val);
if(front->left)
q.push(front->left);
if(front->right)
q.push(front->right);
}
vv.push_back(v);
//当前层出完,下一层都进队列,队列的size()就是下一层的数据个数
levelsize=q.size();
}
return vv;
}
};栈中遵循先进后出的规则,但是队列不遵循这个规则。
