机器人全身控制浅谈：理解 WBC 的原理

概念

WBC（Whole-Body Control，全身控制）是什么？机器人是由"各关节"组成的，其不是"各关节各玩各的"而是一个耦合的整体。在某个时刻可能要做很多事情，比如保持平衡（重心别出圈）、手/脚要动作到目标位置、躯干姿态不能乱、关节不能超限、脚下不能打滑。这些都是一系列任务的组合。

WBC的核心就是把这些任务（目标）和约束（物理/安全）写进一个小型优化问题，在每个控制周期（几百hz~1Khz）求解，得到**"当下这毫秒，各关节应该怎么动/用多大力"**。

一句话总结就是WBC就是用优化的方法求解出要给"关节多少力""以便让机器的各个关节一起配合完成多个目标，且不违反物理与安全约束。

原理

动力学方程

要解释WBC的原理，那必须绕不开动力学方程，这里就先对动力学方程做个简单介绍。

M(q)v˙+h(q,v)=STτ+JcTλ M(q)\dot{v} + h(q,v) = S^T \tau + J_c^T \lambda M(q)v˙+h(q,v)=STτ+JcTλ

配合接触约束：

Jcv=0,λ∈摩擦锥 J_c v = 0,\quad \lambda \in \text{摩擦锥} Jcv=0,λ∈摩擦锥

通俗理解公式就是："惯性 × 加速度 + 自然出现的力 = 电机能给的力 + 地面/物体的反力"

公式左边：机器人自身的自然物理

• M(q)v˙M(q)\dot{v}M(q)v˙：惯性项。M(q)M(q)M(q)是质量矩阵，描述机器人在不同姿态下的惯性特性。\\dot{v} 是广义加速度（关节加速度或身体的加速度）；其意义就像是广义加速度（关节加速度或身体的加速度）；其意义就像是广义加速度（关节加速度或身体的加速度）；其意义就像F=ma里面的里面的里面的ma，表示加速一个有惯性的物体需要的力
• h(q,v)h(q,v)h(q,v)：重力+速度相关项（科氏力、离心力）。如果机器人静止，这里主要就是重力。如果在运动，这里就会出现"速度带来的额外力"，类似开车转弯时身体被甩出去的感觉。

公式右边：外界能提供的"驱动力"

• STτS^T \tauSTτ：电机能施加的关节力矩。τ\tauτ电机产生的力矩（控制器的输出），STS^TST选择矩阵，把电机力矩映射到广义坐标系中。
• JcTλJ_c^T \lambdaJcTλ：接触点反力。λ\lambdaλ来自地面或物体的力（约束反作用力），JcJ_cJc接触点的雅可比，把关节速度映射到接触点速度。JcTλJ_c^T \lambdaJcTλ把"地面推脚的力"转换回"关节的力"。

直观记忆就是类比现实生活中的推车子：

• 你推车：电机力矩τ\tauτ。
• 地面支撑车子：接触反力λ\lambdaλ。
• 车子有质量，要加速就得克服惯性：M(q)v˙M(q)\dot{v}M(q)v˙。
• 重力和转弯的惯性： h(q,v)h(q,v)h(q,v)。

接触力约束

还要满足接触力约束Jcv=0,λ∈摩擦锥J_c v = 0,\quad \lambda \in \text{摩擦锥}Jcv=0,λ∈摩擦锥，其中Jcv=0J_c v = 0Jcv=0意义是接触点速度为0，比如机器人脚贴在地上不滑、不穿透；λ∈摩擦锥\quad \lambda \in \text{摩擦锥}λ∈摩擦锥意义是接触力必须满足摩擦模型，脚不会不穷大摩擦，力要在摩擦椎范围内。

公式中涉及到一个雅可比，什么是雅可比JcJcJc?

假设有一个机械臂：

• 关节角度：就像是控制的"按钮"。
• 手末端的位置：就是最终关心的"结果"。

那么问题就是关节角度动一动，末端的位置会怎么动了？这个"关节空间的微小变化"影响到"末端空间的微小变化"。这样一个映射关系，就是雅可比矩阵JJJ。

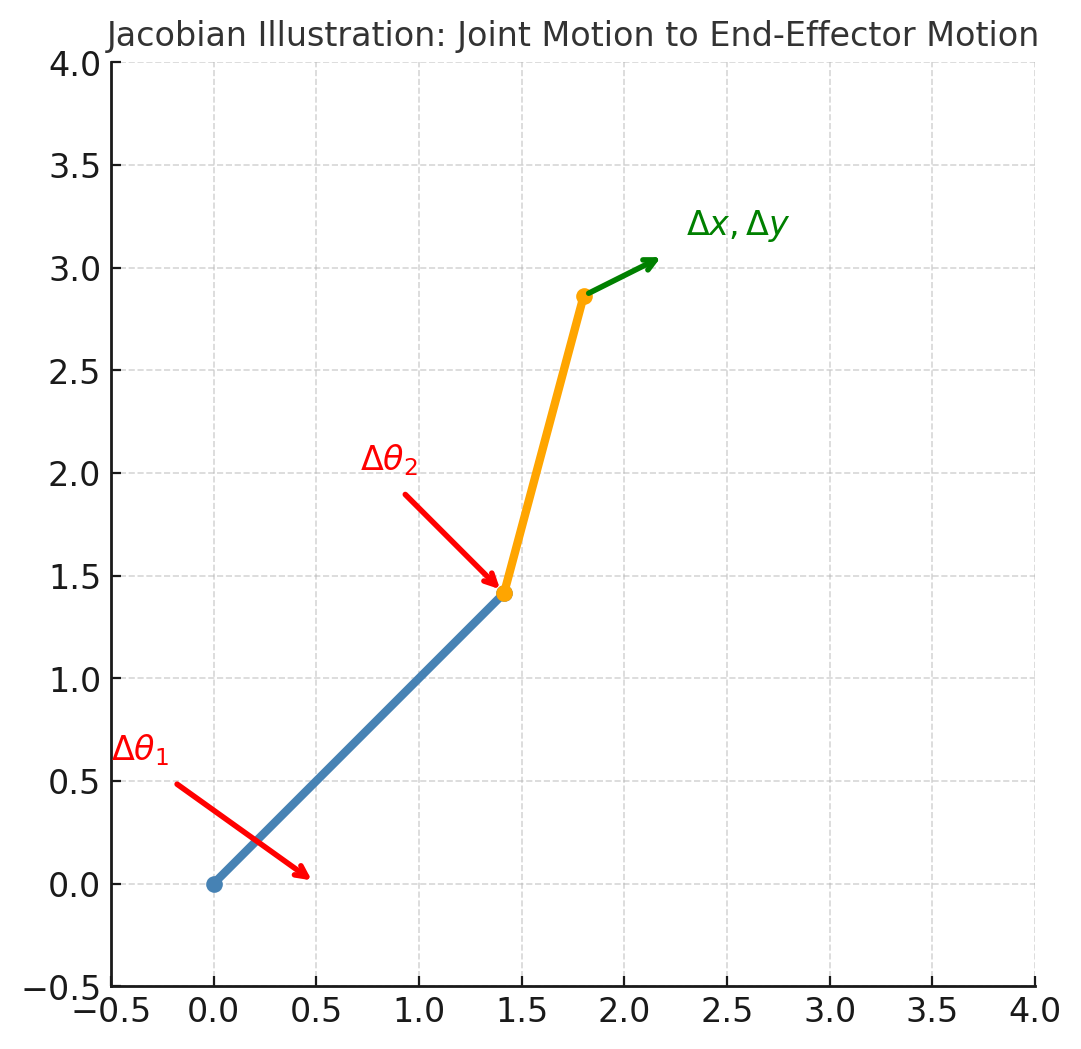
图中红色箭头表示关节角度的小变化Δθ1,Δθ2\Delta \theta_1 , \Delta \theta_2Δθ1,Δθ2。红色箭头的变换导致绿色箭头末端位置的变化：Δx,Δy\Delta x , \Delta yΔx,Δy。雅可比矩阵 JJJ 就是把

Δθ1Δθ2\]⟶\[ΔxΔy\] \\begin{bmatrix}\\Delta \\theta_1 \\\\ \\Delta \\theta_2\\end{bmatrix} \\longrightarrow \\begin{bmatrix}\\Delta x \\\\ \\Delta y\\end{bmatrix} \[Δθ1Δθ2\]⟶\[ΔxΔy

因此如果想要末端动多少就用JJJ，想算末端力传回关节多少就用JTJ^TJT。

总结一下雅可比JJJ就是关节空间和任务空间的桥梁，作用就是我们关节动多少，末端/接触点动多少。

动力学方程在WBC中的用处？

动力学方程是机器人身体运动的"牛顿定律"，我们来看看WBC的目标是什么？WBC不只是让机器人"走"或"站"，而是要全身协调，比如要去抓杯子，脚要保持不滑，躯干要保持平衡，关节力矩不能超过电机限制。所以WBC的本质是解一个优化问题 ，找出一组关节力矩τ\tauτ，既能完成任务目标，又满足动力学方程和约束。

优化问题

WBC的核心思路是把机器人全身的目标任务转化为优化问题，在满足物理规律和约束条件的前提下，求出最合适的一组关节力矩τ\tauτ。

具体一点在WBC中求解的决策变量通常是如下三个：

x=[v˙τλ] x = \begin{bmatrix} \dot{v} \\ \tau \\ \lambda \end{bmatrix} x= v˙τλ

• 最优的关节力矩τ\tauτ。
• 接触点反力λ\lambdaλ。
• 机器人下一步的加速度\\dot{v} 。

优化问题转换为数学的目标函数如下：

min⁡x∥Jtaskv˙−v˙des∥2+∥τ∥2+∥λ∥2 \min_{x} \| J_{\text{task}} \dot{v} - \dot{v}_{\text{des}} \|^2 + \| \tau \|^2 + \| \lambda \|^2 xmin∥Jtaskv˙−v˙des∥2+∥τ∥2+∥λ∥2

公式中Jtaskv˙−v˙desJ_{\text{task}} \dot{v} - \dot{v}{\text{des}}Jtaskv˙−v˙des表示实际加速度与期望加速度的误差，Jtaskv˙J{\text{task}} \dot{v}Jtaskv˙是在当前关节加速度下，末端/任务空的实际加速度，而v˙des\dot{v}_{\text{des}}v˙des是我们期望任务空间实现的期望加速度（比如手往前加速 0.5 m/s²，质心保持 0 加速度）。

同时优化问题还要满足以下约束条件：

• 动力学约束：M(q)v˙+h(q,v)=STτ+JcTλM(q)\dot{v} + h(q,v) = S^T \tau + J_c^T \lambdaM(q)v˙+h(q,v)=STτ+JcTλ。这是硬约束，控制器必须遵守。
• 接触约束：Jcv=0J_c v = 0Jcv=0，接触点不能乱动（不滑、不穿透）。
• 摩擦约束：λ∈Kfric\lambda \in \mathcal{K}_{\text{fric}}λ∈Kfric，接触力必须符合摩擦模型（不能无限大）。
• 力矩限制：τmin⁡≤τ≤τmax⁡\tau_{\min} \leq \tau \leq \tau_{\max}τmin≤τ≤τmax。

总结一下优化问题的目标函数意思就是要满足任务误差最小化（手/身体/质心的加速度跟踪目标），同时要满足能量或力矩最小化（不能浪费力），同时满足接触力正则化（力要稳定不能乱跳）。

方程有了，怎么求解了？

这个目标函数是一个二次型，符合QP，所以可以用现成的QP求解器来解，例如：OSQP、qpOASES、Gurobi（商业求解器）、CPLEX（商业求解器）、CVXPy（Python 封装，常用于原型），这里就不过多阐述了。

总结一下WBC核心就是要解决一个优化问题：二次目标（误差最小 + 力矩正则） + 动力学/接触/摩擦/限幅约束。其求解的方式通常使用QP 求解器（实时、高效、全局最优）。求解的结果是关节力矩τ\tauτ（给电机执行），同时还得到加速度v˙\dot{v}v˙和接触力λ\lambdaλ。

示例

接下来我们调用cvxpy库看看示例，直观体验一下。

import cvxpy as cp
import numpy as np

# ---- 机械臂参数 ----
l1, l2 = 1.0, 1.0
m1, m2 = 1.0, 1.0
theta1, theta2 = np.deg2rad(45), np.deg2rad(30)

# ---- 雅可比（末端位置对关节的导数）----
J_task = np.array([
    [-l1*np.sin(theta1) - l2*np.sin(theta1+theta2), -l2*np.sin(theta1+theta2)],
    [ l1*np.cos(theta1) + l2*np.cos(theta1+theta2),  l2*np.cos(theta1+theta2)]
])

# ---- 动力学质量矩阵 M（简化版）----
M = np.array([
    [m1*l1**2 + m2*(l1**2 + l2**2 + 2*l1*l2*np.cos(theta2)), m2*(l2**2 + l1*l2*np.cos(theta2))],
    [m2*(l2**2 + l1*l2*np.cos(theta2)), m2*l2**2]
])
h = np.zeros(2)  # 忽略重力/科氏项

# ---- 接触约束：假设末端y方向不能动（竖直方向约束）----
Jc = np.array([[0, 1]]) @ J_task   # 取末端y方向的行

# ---- 变量 ----
ddq = cp.Variable(2)   # 关节加速度
tau = cp.Variable(2)   # 力矩
lam = cp.Variable(1)   # 接触力 (竖直反作用力)

# ---- 期望任务加速度（末端x方向=1.0, y方向=0.0）----
xddot_des = np.array([1.0, 0.0])

# ---- 目标函数：末端任务 + 力矩/接触力正则 ----
objective = cp.Minimize(
    cp.sum_squares(J_task @ ddq - xddot_des) +
    0.01*cp.sum_squares(tau) +
    0.01*cp.sum_squares(lam)
)

# ---- 约束 ----
constraints = [
    M @ ddq + h == tau + Jc.T @ lam,   # 动力学方程
    Jc @ ddq == 0,                     # 接触点不加速
    tau >= -10, tau <= 10,
    lam >= 0                           # 接触力必须向上推
]

# ---- 求解 ----
prob = cp.Problem(objective, constraints)
prob.solve()

print("Optimal joint accelerations:", ddq.value)
print("Optimal torques:", tau.value)
print("Optimal contact force λ:", lam.value)
print("End-effector acc achieved:", J_task @ ddq.value)
print("Desired end-effector acc   :", xddot_des)

上面的示例中可以分为几部分：

（1）任务

末端（手）在水平 xxx 方向产生 1.0m/s21.0 \text{m/s}^21.0m/s2 的加速度。在垂直 yyy 方向不要加速（因为手撑在桌子上，不应该离开桌面）。

数学写法：

x¨des=[1.0,0.0]T \ddot{x}_{des} = [1.0,0.0]^T x¨des=[1.0,0.0]T

（2）决策变量

优化器要决定的量是

q¨=[θ¨1,θ¨2]T,τ=[τ1,τ2]T,λ \ddot{q} = [\ddot{\theta}_1,\ddot{\theta}_2]^T, \quad \tau = [\tau_1,\tau_2]^T, \quad \lambda q¨=[θ¨1,θ¨2]T,τ=[τ1,τ2]T,λ

（3）要优化的目标函数

最小化

min⁡q¨,  τ,  λ∥Jtaskq¨−x¨des∥2+0.01∥τ∥2+0.01∥λ∥2 \min_{\ddot{q},\;\tau,\;\lambda}\| J_{\text{task}} \ddot{q} - \ddot{x}_{des} \|^2+ 0.01 \|\tau\|^2+ 0.01 \|\lambda\|^2 q¨,τ,λmin∥Jtaskq¨−x¨des∥2+0.01∥τ∥2+0.01∥λ∥2

（4）约束条件

• 动力学约束：M(q)q¨+h(q,q˙)=τ+JcTλM(q)\ddot{q} + h(q,\dot{q}) = \tau + J_c^T \lambdaM(q)q¨+h(q,q˙)=τ+JcTλ
• 接触约束：Jcq¨=0J_c \ddot{q} = 0Jcq¨=0
• 力矩范围：−10≤τi≤10-10 \leq \tau_i \leq 10−10≤τi≤10
• 接触力非负：λ≥0\lambda \geq 0λ≥0

（5）输出结果

最后调用

prob = cp.Problem(objective, constraints)
prob.solve()

求解得出结果：

Optimal joint accelerations: [ 0.50615867 -1.88900987]
Optimal torques: [-1.12977187 -0.94450493]
Optimal contact force λ: [1.29515155e-23]
End-effector acc achieved: [ 9.77823461e-01 -5.00938335e-17]
Desired end-effector acc   : [1. 0.]

QP 解出来的就是

• 最优关节加速度：q¨\ddot{q}q¨
• 最优关节力矩：τ\tauτ
• 接触反力：λ\lambdaλ
• 实际末端加速度：x¨=Jtaskq¨\ddot{x} = J_{\text{task}} \ddot{q}x¨=Jtaskq¨

并与期望值 x¨des\ddot{x}_{des}x¨des 对比。

上面的代码中只截取了关键部分，下面是绘制图像的效果如下，可以直观体会看看：

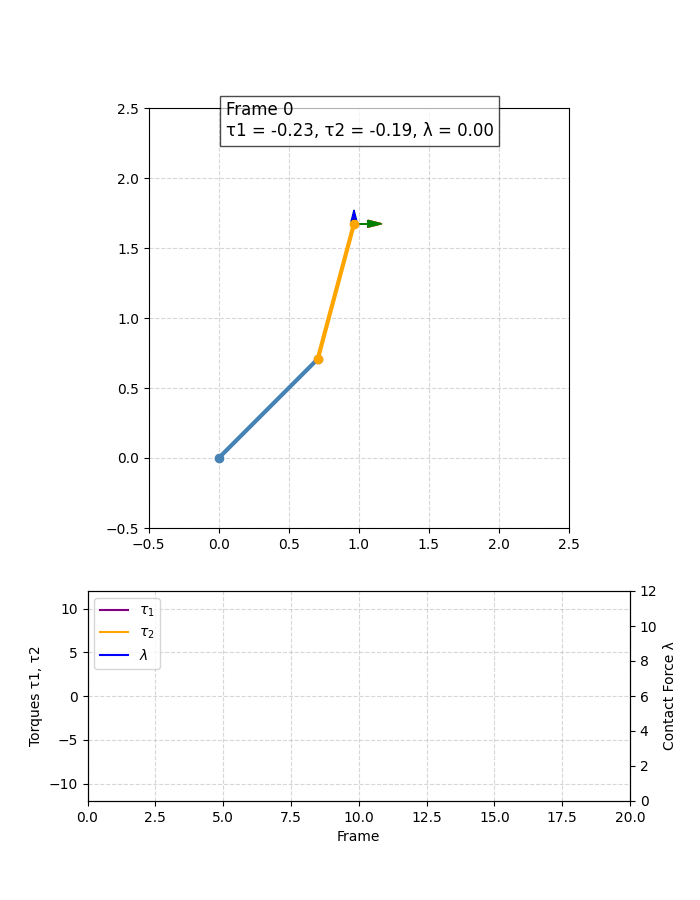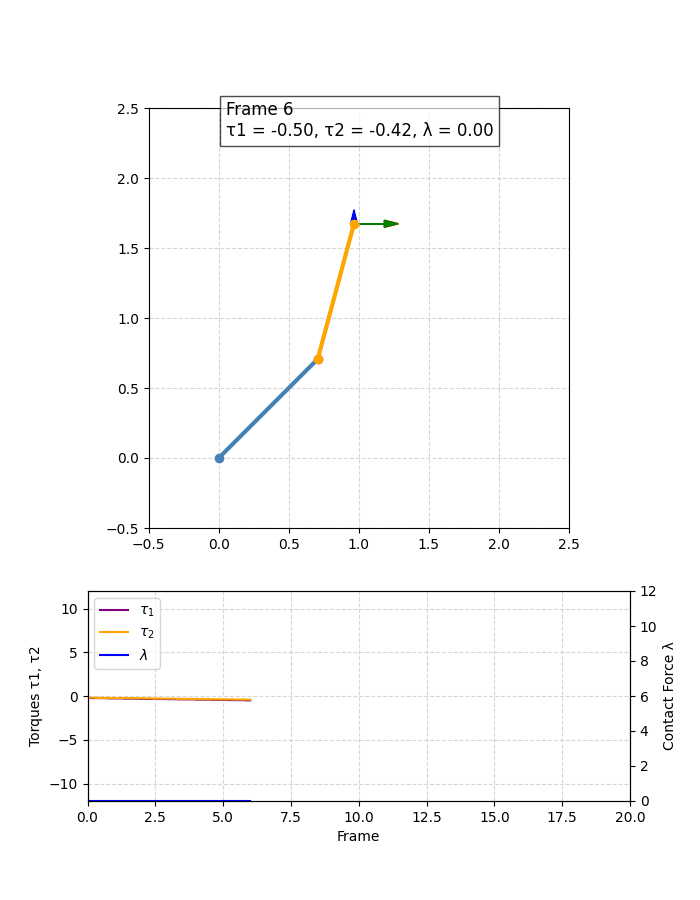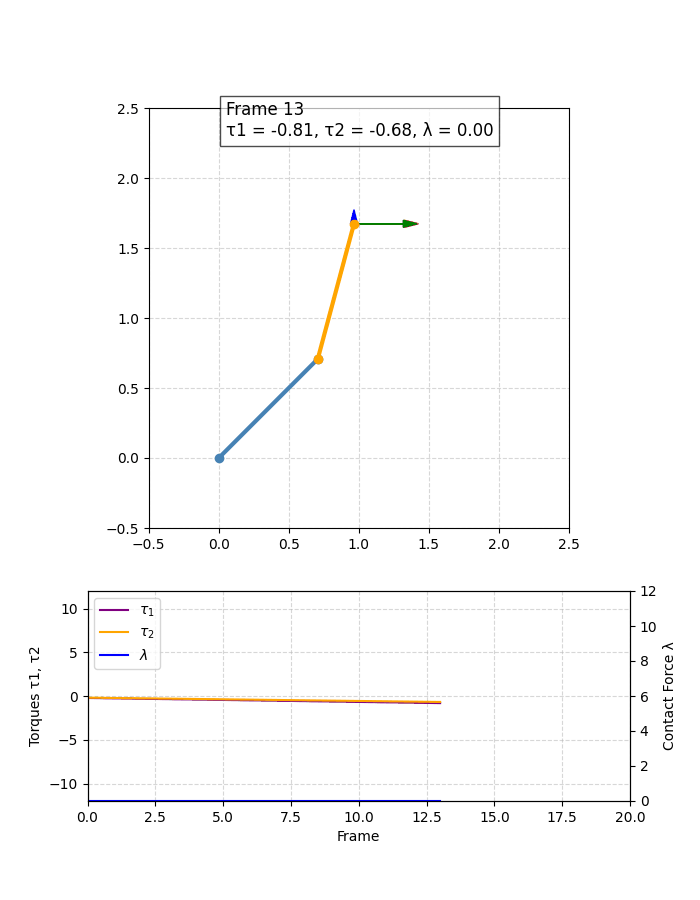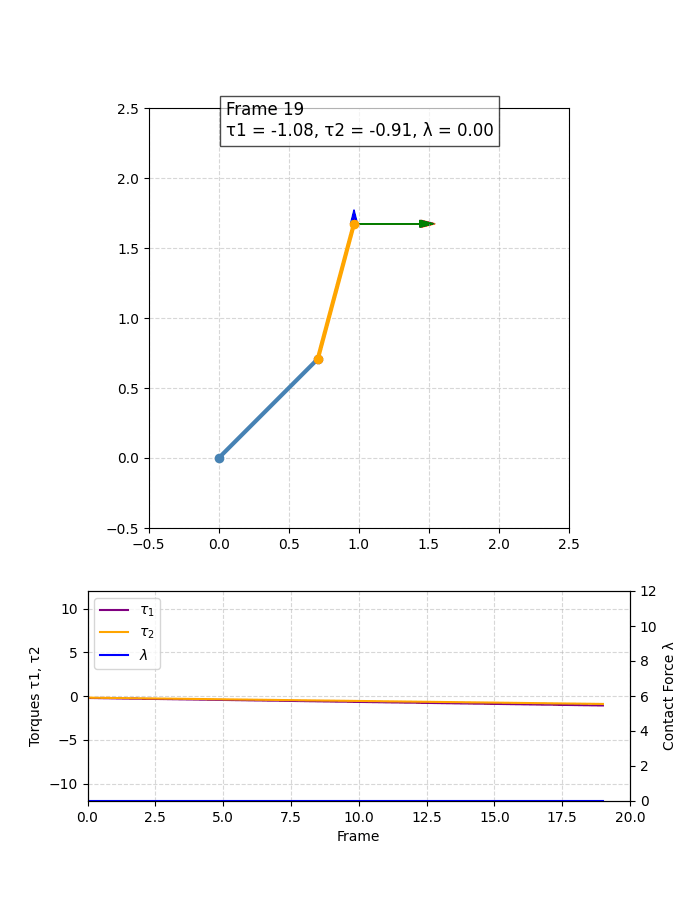
WBC与MPC

上一篇文章我们分析了MPC，那么MPC与WBC什么关系了？

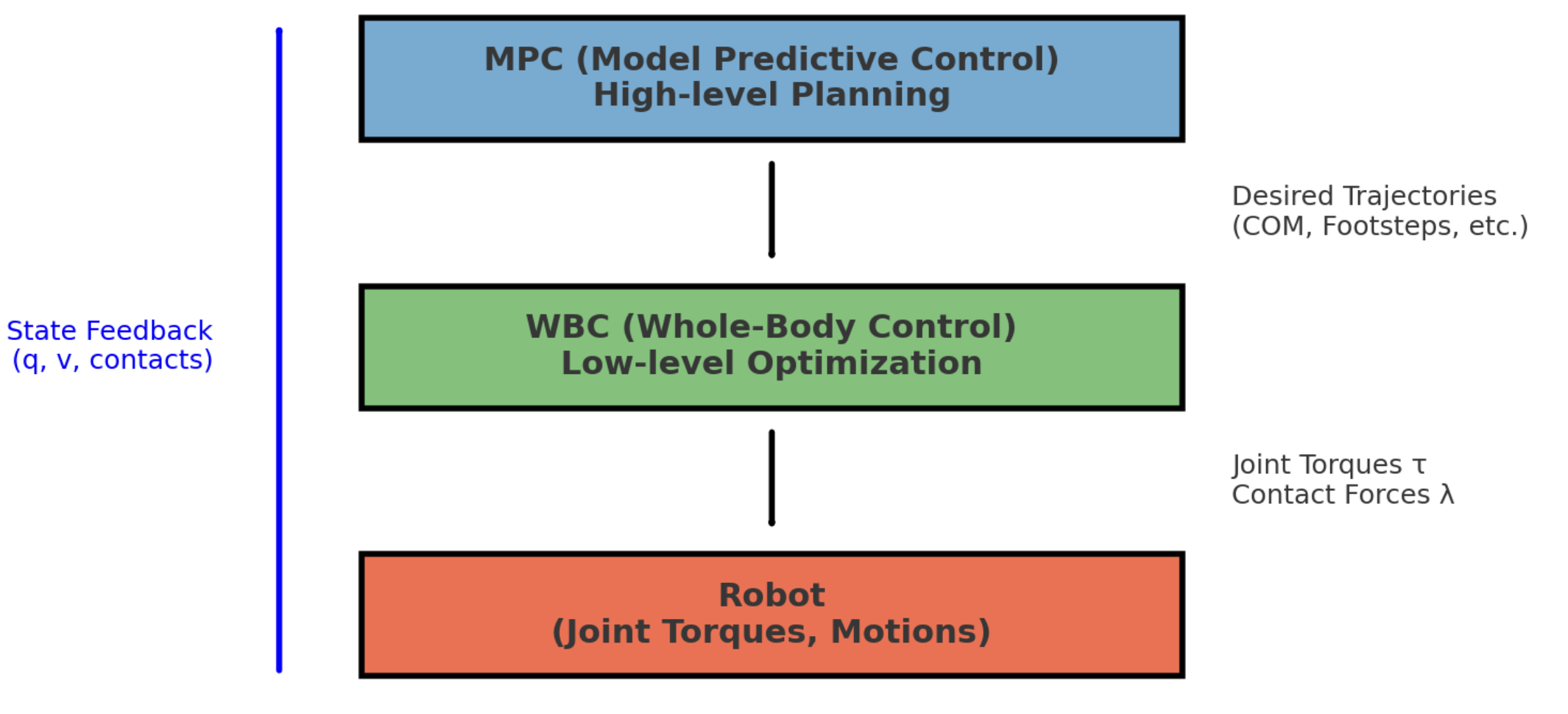
MPC在WBC之上，MPC作为决策层做"未来几步的规划"，比如预测未来1S内，质心应该怎么移动，脚该放哪里，其输出的是期望的任务轨迹。WBC是在下层，拿到MPC给的任务（目标加速度/姿态/接触序列）在动力学和接触约束下，求解QP得到当下这一瞬间的关节力矩τ\tauτ。简而言之MPC决定"机器人未来要往哪走"，WBC决定"当前每个关节该怎么出力"。

举个例子：双足机器人走路

• MPC：优化未来 1 秒的 质心轨迹、摆腿位置、支撑相切换。输出：期望的 x¨des\ddot{x}_{des}x¨des（质心加速度）、脚的落点计划。
• WBC：把这些期望当作任务输入，解 QP ，输出关节力矩 τ\tauτ，同时计算接触力 λ\lambdaλ，保证机器人在每一步不摔倒。