C++ 二分算法(1)

二分算法是一个很简单的算法但是呢我们在实际操本次我作的时候往往很难控制边界

本次主要讲解两种二分算法

以leetcode 704题为例

1.第一种

第一种二分算法

也是大部分人常用的算法

二分法算法和滑动窗口一样本质上是一种特殊的双指针算法

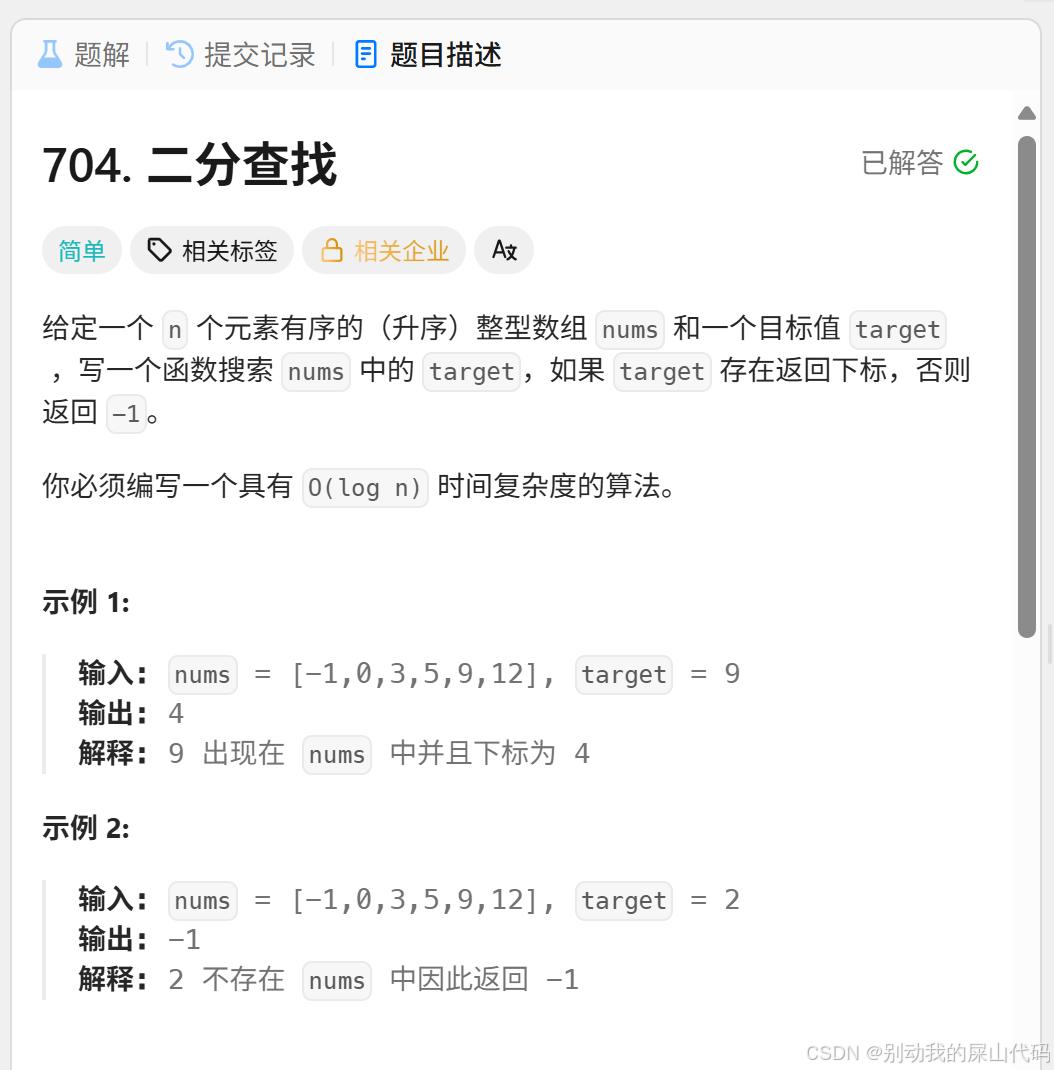
Example:nums={-1,0,3,5,9,12,17,23} target=3

二分的位置我们设置为mid

mid这个地方设置成****

问题1 mid为什么不设置成呢

因为left值在int 范围内 right值在left范围内但是left+right可能溢出int可表示的值导致截断

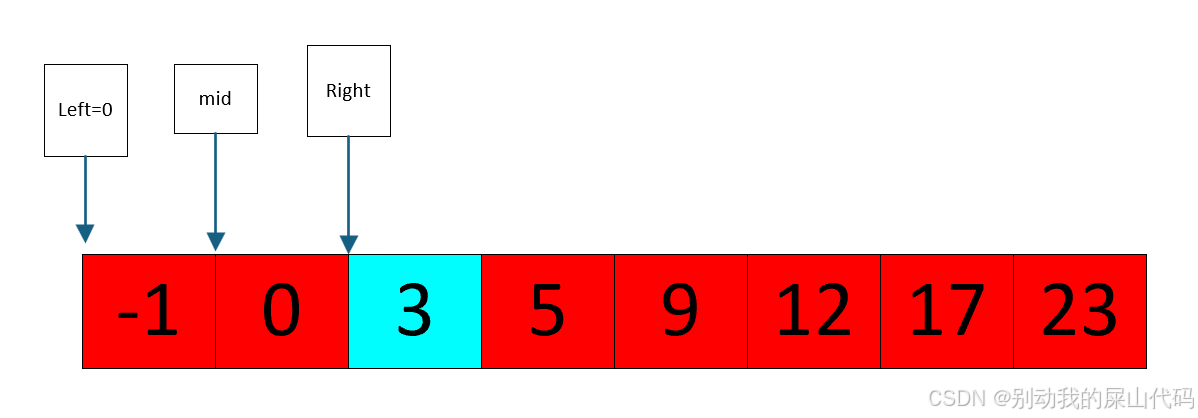
起始状态 left=0 right=7 mid=0+3=3

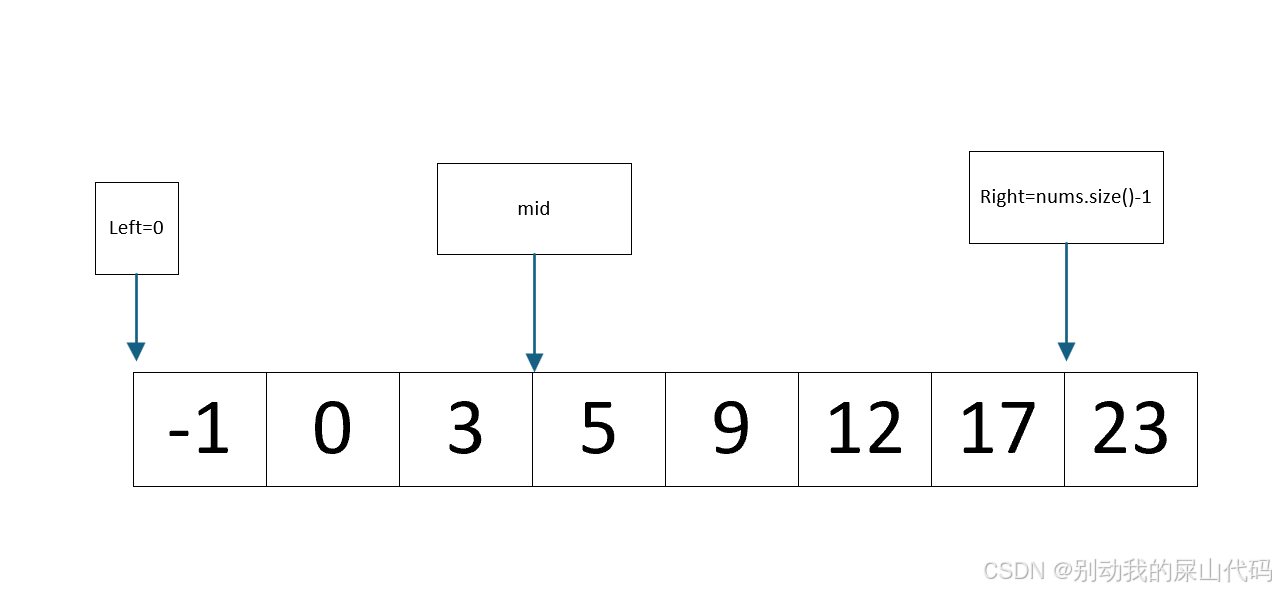
此时我们判断 nums[mid]=5>target=3

说明 target不可能存在于下图mid和right之间

也就是不可能存在于5到23之间

******我们看范围是以元素为单位看范围

不是以指针指向的区间为单位看范围******

也就是不可能存在于下图红色的区域

也就是说target只可能存在于下图蓝色区域的位置(即-1到3之间)

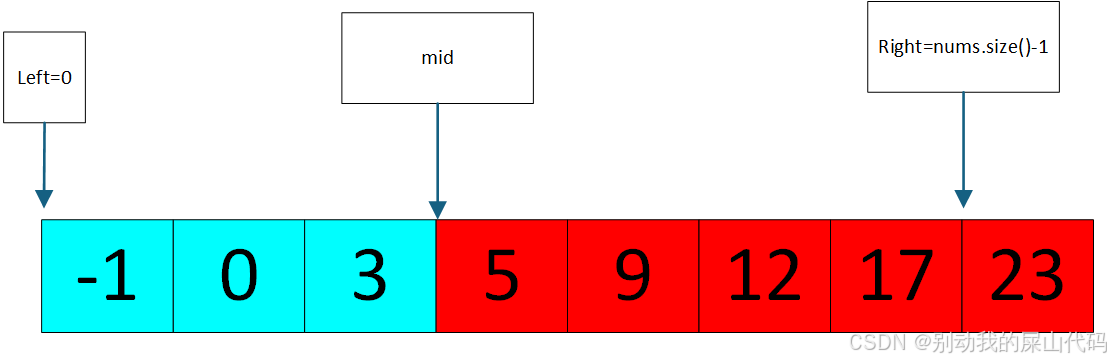
所以下一次二分的末尾也就是下一次二分right的位置应该指向蓝色区域的最后一个元素

也就是right应该指向3

转换成1代码就是right=mid-1;

mid重新计算即可

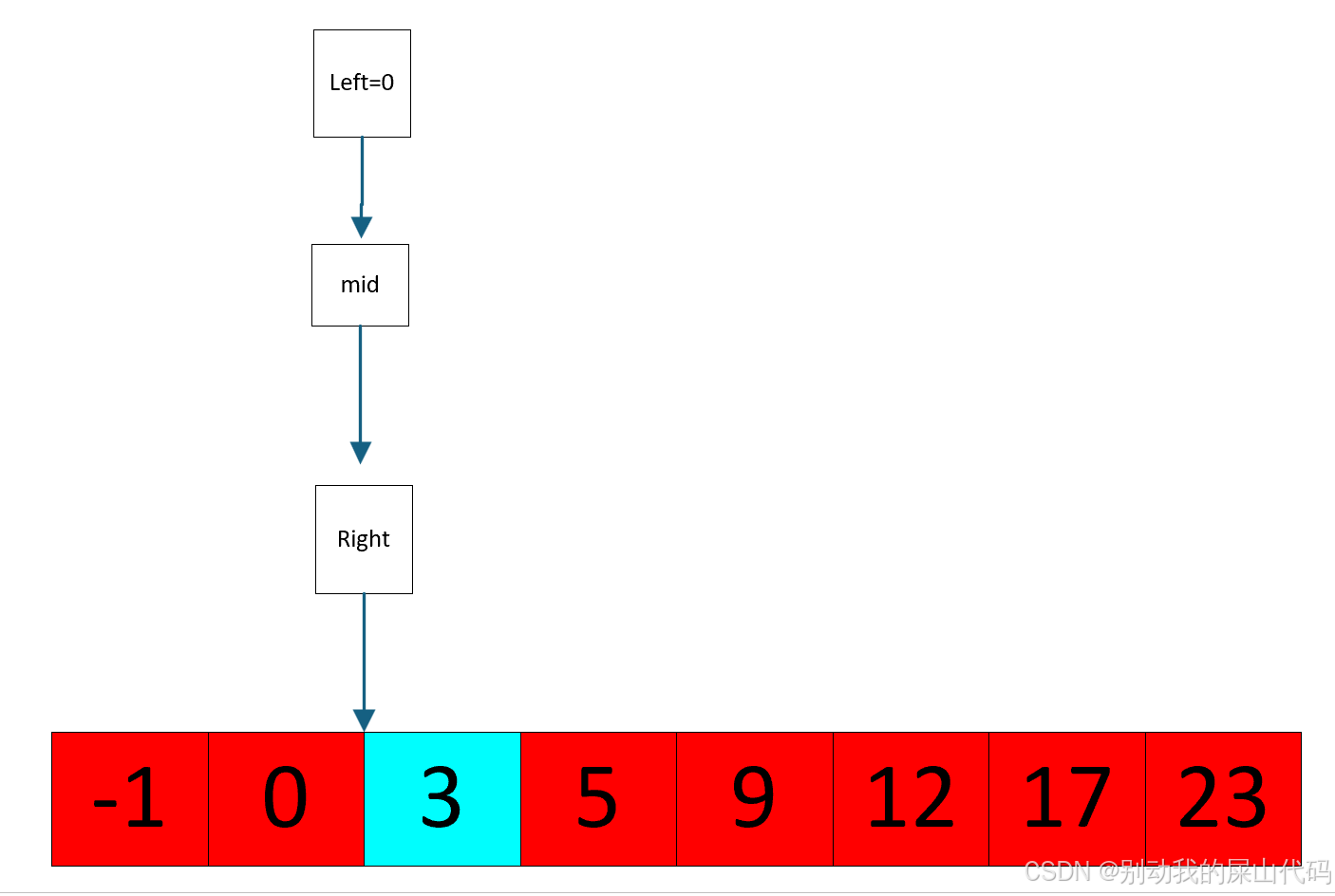
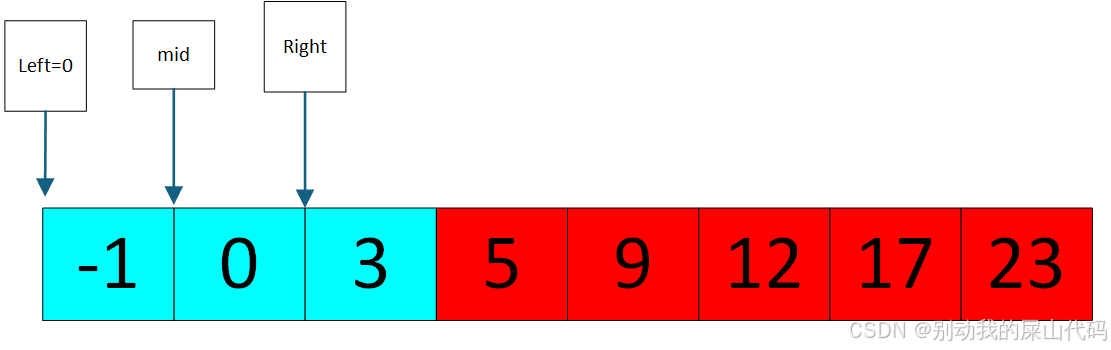此时我们判断 nums[mid]=0<target=3

说明 target不可能存在于mid和left之间（即-1到0）
也就是不可能存在于于下图面红色的区域
也就是说target只可能存在于下图蓝色区域的位置

所以下一次二分的末尾也就是下一次二分left的位置应该指向蓝色区域的最后一个元素
也就是left应该指向3
转换成1代码就是left=mid+1;

mid重新计算即可

此时mid left right 三和一我们就找到了我们想要的值

所以这个时候我们可以简单实现一下二分算法的部分码了

cpp 复制代码

while (停止条件) {
	mid = left + (right - left) / 2;
	if (nums[mid] > target) {
		right = --mid;
	}
	else if (nums[mid] < target) {
		left = ++mid;
	}
	else {
		return mid;
	}
}

但是这个地方我们还要思考一个问题

就是如果这个数组没有这个值那么这个二分思路什么时候停下来？？？

思路一：可不可以写left=right的时候停下来呢？？？

也就是进入循环的条件是left!=right

答案是不可以的

因为当只有一个元素的时候也就是nums.size=1的时候

最开始left和right就相同压根不会进入循环

当然两个元素的时候也会出事这个地方不做多介绍

有兴趣可以自己去尝试画一下 nums={2,5} target=5的图

原本应该返回1 但是实际返回值是-1

思路二：可不可以left>right的时候停下来呢？？？

也就是进入循环就是left<=right

我们发现每一次二分left离right越来越近

既然left=right作为停止条件不可以

那么left>=right作为停止条件肯定也是不可以的

那么lef>tright作为停止条件可以吗？？？

如果可以为什么？？？

首先呢当我们

当target不存在于nums中

这个地方我们把最开始的那个例子的第三个元素的值改成了2

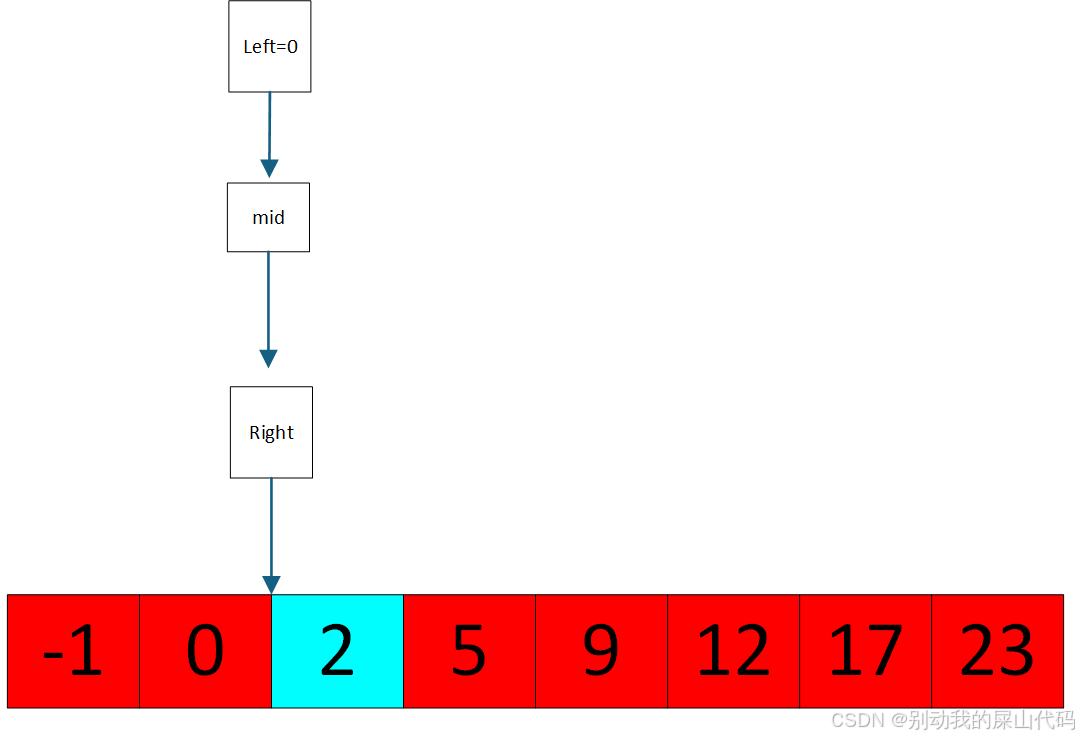
此时 nums[mid]<target

所以按照前面代码的逻辑

此时left=mid+1;

所以此时呢

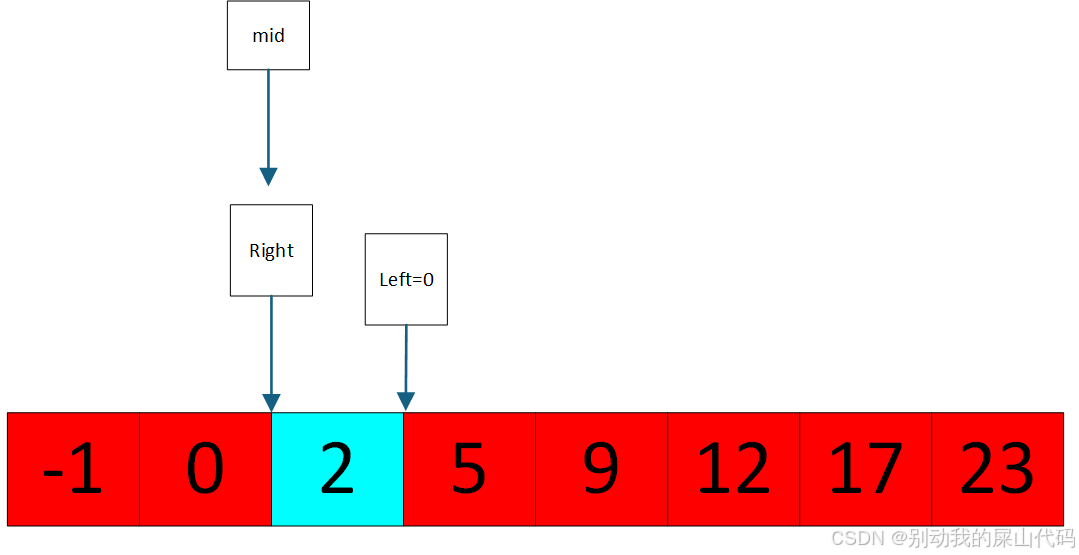
此时left>mid的停止条件完全没有问题

当然我们也可以试一下

一个元素或者说两个元素的情况下

这是完全没有问题的

为什么呢？

1.避免了死循环问题

因为每一次没有找到目标值的时候

left至少像右走了一步或者right至少想左走一步这两个至少有一个是要执行的

至于为什么是至少走一步（当left或者right一边与mid重合的时候就可能会只走一步**）**

所以说left>right完全是可以实现的

不会陷入死循环

2.left==right的时候可能会导致一些正确的数据被判错误

我们每一次while循环没找到时候

都会导致left和right移动

但是移动后如果left和right指向同一个位置且值与target相同

但是我要判断nums[left]和target是否相同我就要进入循环呀

但是这个时候如果left==right作为停止条件

我进入不了循环所以就无法判断呀

所以当left==right作为停止条件的时候我们还可能漏掉情况

所以这个时候就不能停止

那么为什么left>right可以呢？

因为此时我已经把所有元素都遍历了当然不会再有可能存在的情况呀

当然呢如果你说我硬要写left>=right作为循环停止条件可以吗

也就是left<right作为进入while条件也可以

但是你每次left==right的时候都要判断nums[left] 是否等于target

当然你可以说我每次while改变left和right后判断

但是有时候left和right初始化的时候就是相同的

比如只有一个元素的时候

这个时候我就要单独加一个if语句在while循环前判断

但是依然不推荐因为这样代码就会有点臃肿

cpp 复制代码

class Solution {
public:
    int search(vector<int>& nums, int target) {
         if (nums.size() == 0) {
            return -1;
        }
             if (nums.size() == 1) {
            if (nums[0] == target)
                return 0;
            else
                return -1;
        }
        int left = 0;
        int right = nums.size() - 1;
        int mid;
        while (left< right) {
            mid = left + (right - left) / 2;
            if (nums[mid] > target) {
                right = --mid;
                 if(left==right&&nums[right]==target)
                return right;
            } else if (nums[mid] < target) {
                left = ++mid;
                if(left==right&&nums[left]==target)
                return left;
            } else {
                return mid;
            }
        }
        return -1;
    }
};

但是如果我要写left==right作为while的停止条件可以吗？

可以但是相比 left>right作为停止条件还需要注意下面的情况

比如 left=0 mid=0 right=1 nums[mid]>target 此时right>left

然后 right=--mid right=-1 此时 right<left

这个地方我们就跳过了left==right

所以对于循环停止我们还要多写一种情况也就是right<0

也就是进入while循环条件要加right>-1

产生这种情况这和我们mid的计算方法有关系

核心在于计算mid有一步是/2 但是整数的/2 会截断比如3/2=1；

这就会导致mid指向的位置偏小也就是偏左

但是右端你不用担心在mid偏小的时候 left=++mid 你更难越界

比如 left=nums.size()-2 right=nums.size()-1 mid=nums.size()-2 nums[mid] <target 此时right>left

然后 left=++mid; left=nums.size()-1 right=nums.size()-1 此时left==right

cpp 复制代码

class Solution {
public:
	int search(vector<int>& nums, int target) {
		if (nums.size() == 0) {
			return -1;
		}
		if (nums.size() == 1) {
			if (nums[0] == target)
				return 0;
			else
				return -1;
		}
		int left = 0;
		int right = nums.size() - 1;
		int mid;
		while (left != right&&right>-1) {
			mid = left + (right - left) / 2;
			if (nums[mid] > target) {
				right = --mid;
				if (left == right && nums[right] == target)
					return right;
			}
			else if (nums[mid] < target) {
				left = ++mid;
				if (left == right && nums[left] == target)
					return left;
			}
			else {
				return mid;
			}
		}
		return -1;
	}
};

由此我们确定了做好的停止条件是left>right

也就是进入while的条件是 while(left<=right)

由此我们就可以完善我们的代码了

cpp 复制代码

class Solution {
public:
    int search(vector<int>& nums, int target) {
         if (nums.size() == 0) {
            return -1;
        }
        int left,mid = 0;
        int right = nums.size() - 1;
        while (left<= right) {
            mid = left + (right - left) / 2;
            if (nums[mid] > target) {
                right = --mid;
            } else if (nums[mid] < target) {
                left = ++mid;
            } else {
                return mid;
            }
        }
        return -1;
    }
};