目录
[1. 神经网络最优化问题的挑战](#1. 神经网络最优化问题的挑战)
[2. SGD方法及其实现](#2. SGD方法及其实现)
[3. SGD的缺点分析](#3. SGD的缺点分析)
[1. Momentum方法](#1. Momentum方法)
[2. AdaGrad方法](#2. AdaGrad方法)
[3. Adam方法](#3. Adam方法)
[1. 四种方法可视化对比](#1. 四种方法可视化对比)
[2. 算法选择建议](#2. 算法选择建议)
一、参数更新与SGD的局限性
1. 神经网络最优化问题的挑战
神经网络的学习本质上是寻找使损失函数最小化的参数过程,这被称为最优化问题。然而,神经网络的最优化面临两大挑战:
-
参数空间复杂:无法通过解析方法直接求得最优解
-
参数数量庞大:深度网络中的参数可达数百万甚至数十亿
探险家比喻 :寻找最优参数就像蒙眼探险家在广阔地形中寻找最深山谷 ,只能依靠脚下**坡度(梯度)**作为唯一线索。
2. SGD方法及其实现
随机梯度下降法(SGD)是最基础的优化方法,在**《AI学习日记------线性回归》**中有详细介绍:
数学表达式:
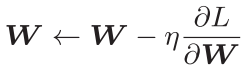
代码实现:
class SGD:
def init(self, lr=0.01 ): #一般情况下固定为0.01或0.001
self.lr = lr # 学习率
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]
使用示例:
network = TwoLayerNet(...)
optimizer = SGD(lr=0.01)
for i in range(10000):
x_batch, t_batch = get_mini_batch(...)
grads = network.gradient(x_batch, t_batch)
optimizer.update(network.params, grads) # 更新参数
实例化optimizer负责完成参数更新,只需要将参数和梯度的信息传给optimizer。
3. SGD的缺点分析
SGD在处理**非均向函数(多变量时【不同方向/不同变量】上的"坡度"不同)**时效率低下:
-
呈"之"字形移动路径,搜索效率低
-
梯度方向并不总指向最小值方向
-
对所有变量使用相同的学习率
二、改进的优化算法
1. Momentum方法
Momentum模拟了物理学中的动量 概念,使优化过程像小球在斜面上滚动。让每个点加上上一个点的更新方向向量,模拟惯性。
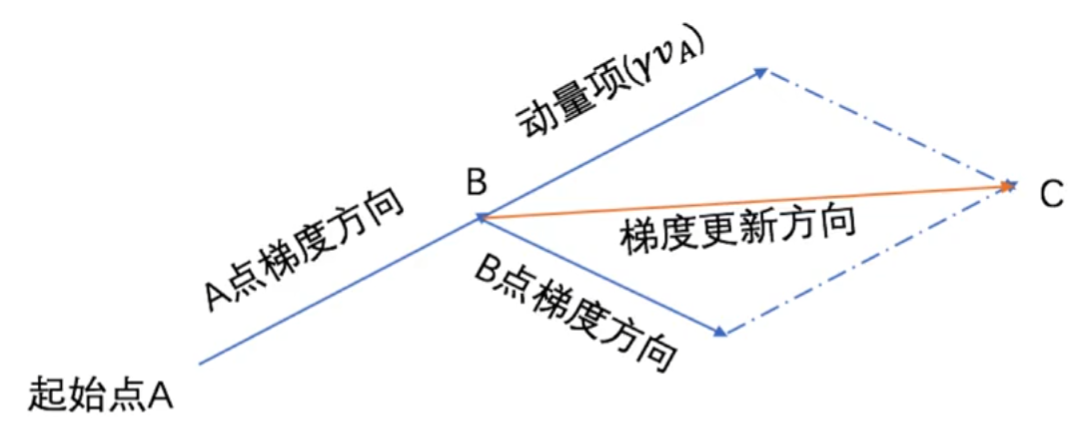
数学原理:
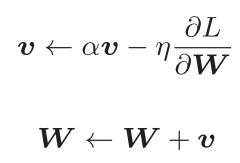
Python实现:
class Momentum:
def init(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum #惯性学习率
self.v = None # 保存的上一个点的更新方向
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
params[key] += self.v[key]
优势:
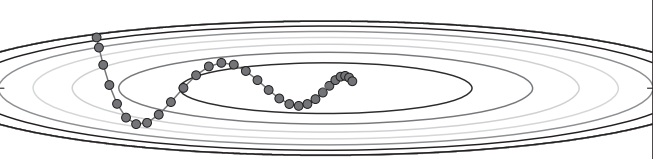
-
抑制"之"字形振荡
-
在梯度方向一致的维度上加速
-
在梯度方向变化的维度上减速
2. AdaGrad方法
AdaGrad为每个参数自适应地调整学习率a 。除以h:以前的所有梯度值的平方和 开根,用来判断此前移动幅度大小。更新幅度大,学习率下降大;更新幅度小,学习率下降的小。
数学原理:
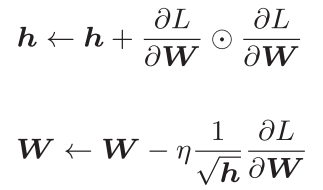
Python实现:
class AdaGrad:
def init(self, lr=0.01):
self.lr = lr
self.h = None # 梯度平方和累积
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7 ) #防止梯度为0
特点:
-
频繁更新的参数学习率变小
-
稀疏更新的参数学习率保持较大
-
自动进行学习率衰减
局限性:
-
学习过程中更新量会越来越小
-
可能过早停止学习(可通过RMSProp改进)
3. Adam方法
Adam结合了Momentum和AdaGrad的优点,是当前最流行的优化算法。
核心思想:
-
使用动量项加速收敛
-
自适应调整每个参数的学习率
-
包含偏置校正机制
Python实现:
非常复杂,这里不展示update细节,宏观理解即可,包含一阶矩估计,二阶矩估计**,**偏执矫正的思想。
class Adam:
def init(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1 # 一次momentum系数
self.beta2 = beta2 # 二次momentum系数
self.iter = 0
self.m = None # 一次momentum
self.v = None # 二次momentum
def update(self, params, grads):
**# 具体实现包含偏置校正等细节
...**
超参数设置:
-
学习率α:通常设为0.001
-
β1:0.9(一次momentum系数)
-
β2:0.999(二次momentum系数)
三、优化算法比较与实践
1. 四种方法可视化对比
在测试函数 f(x, y) = (1/20)x² + y² 上的表现:
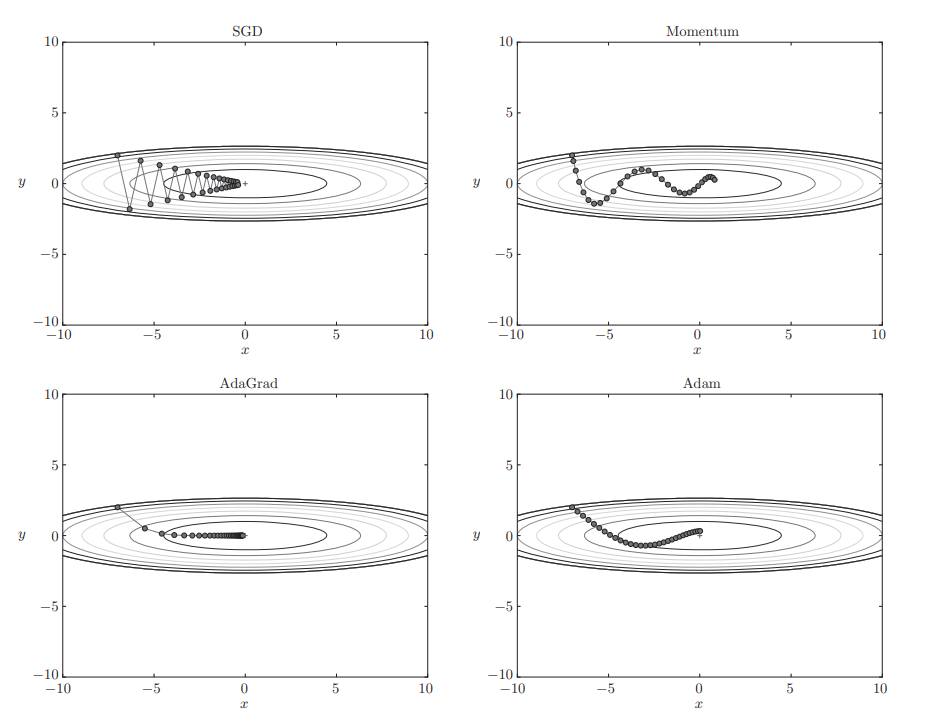
2. 算法选择建议
-
首选Adam:在大多数情况下表现良好
-
备用SGD:当Adam效果不佳时尝试
-
学习率调整:Adam的默认学习率0.001通常效果很好
-
批量大小:与优化算法配合调整
总结
本文介绍了神经网络优化的主要方法及其改进。首先分析了SGD的局限性,包括效率低下和单一学习率问题。随后详细介绍了三种改进算法:Momentum(模拟物理动量)、AdaGrad(自适应学习率)和Adam(结合两者优势)。通过可视化对比,Adam在多数情况下表现最优,建议作为首选算法,同时保留SGD作为备选方案。实践时需注意学习率和批量大小的调整。