机器学习:决策树
决策树
决策树概念
决策树是一种常用的分类模型。其整体构成一个树模型,自上而下进行判断。通过一系列if-then规则将数据层层划分,直到得到最终结论。
信息熵
信息熵指的是数据集的不确定性。即一个数据集的混乱程度。其计算方式如下:
H ( S ) = − ∑ i = 1 N p i l o g 2 p i H(S) = -\sum_{i=1}^N p_i \mathrm{log_2}p_i H(S)=−i=1∑Npilog2pi
其中 S S S为原数据集, p i p_i pi为对应类别 i i i的概率, N N N为类别数量。
信息增益
信息增益是指在根据某个特征进行分裂后,如果信息熵减小了,即数据集的不确定性减小了,则这个减小的数值就是信息增益。
I G ( S , A ) = H ( S ) − H ( S ∣ A ) IG(S,A)=H(S)-H(S|A) IG(S,A)=H(S)−H(S∣A)
其中, H ( S ) H(S) H(S)为数据集 S S S的信息熵, H ( S ∣ A ) H(S|A) H(S∣A)为按照特征 A A A分裂后的信息熵。但是信息增益引起一个问题,在分裂准则上,其更偏好多值特征。举个例子:
| 学生ID | 学习时长(h) | 做题数量 | 是否通过 |
|---|---|---|---|
| 001 | 5 | 20 | 是 |
| 002 | 3 | 10 | 是 |
| 003 | 5 | 15 | 是 |
| 004 | 6 | 25 | 是 |
| 005 | 3 | 5 | 否 |
原始信息熵:
H ( S ) = − ( 4 5 l o g 2 4 5 + 1 5 l o g 2 1 5 ) = 0.7219 H(S)=-(\frac45 \mathrm{log_2} \frac45+\frac15 \mathrm{log_2}\frac15)=0.7219 H(S)=−(54log254+51log251)=0.7219
按照"学生ID"进行分裂,因为学生ID是唯一的,所以信息熵为0:
H ( S ∣ 学生 I D ) = 0 H(S|学生ID)=0 H(S∣学生ID)=0
按照"学习时长"进行分裂,有3个类别,信息熵为:
H ( S ∣ 学习时长 = 5 ) = 0 H(S|学习时长=5)=0 H(S∣学习时长=5)=0
H ( S ∣ 学习时长 = 3 ) = − ( 1 2 l o g 2 1 2 + 1 2 l o g 2 1 2 ) = 1 H(S|学习时长=3)=-(\frac12 \mathrm{log_2}\frac12 + \frac12 \mathrm{log_2}\frac12) = 1 H(S∣学习时长=3)=−(21log221+21log221)=1
H ( S ∣ 学习时长 = 6 ) = 0 H(S|学习时长=6)=0 H(S∣学习时长=6)=0
所以 H ( S ∣ 学习时长 ) = 2 5 × 0 + 2 5 × 1 + 1 5 × 0 = 0.4 H(S|学习时长)=\frac25\times 0 +\frac25\times1+\frac15\times 0=0.4 H(S∣学习时长)=52×0+52×1+51×0=0.4
按照"做题数量"进行分裂,做题数量数量唯一,所以信息熵为0:
H ( S ∣ 做题数量 ) = 0 H(S|做题数量) = 0 H(S∣做题数量)=0
则上述三个分类特征信息增益:
(1)按照"学习时长"进行分裂,信息增益:
I G = 0.7219 − 0.4 = 0.3219 IG = 0.7219-0.4=0.3219 IG=0.7219−0.4=0.3219
(2)按照"学生ID"和"做题数量"进行分裂,信息增益:
I G = 0.7219 − 0 = 0.7219 IG=0.7219-0=0.7219 IG=0.7219−0=0.7219
优先按照信息增益大的特征分裂,但是事实中,这样并不合理。且容易造成"过拟合"。
信息增益率
信息增益率是用来解决多值特征问题,其计算方式如下:
G a i n R a t i o n ( S , A ) = I G ( S , A ) I V ( A ) GainRation(S,A)=\frac{IG(S,A)}{IV(A)} GainRation(S,A)=IV(A)IG(S,A)
其中:
- I G ( S , A ) IG(S,A) IG(S,A):按照特征A分裂的信息增益
- I V ( A ) IV(A) IV(A):固有值,衡量特征A的分类能力
- I V ( A ) IV(A) IV(A): − ∑ v ∈ V a l u e ( A ) ∣ S v ∣ ∣ S ∣ l o g 2 ∣ S v ∣ ∣ S ∣ -\sum_{v \in Value(A)} \frac{|S_v|}{|S|}\mathrm{log_2} \frac{|S_v|}{|S|} −∑v∈Value(A)∣S∣∣Sv∣log2∣S∣∣Sv∣
基尼系数
基尼系数公式为:
G i n i ( S ) = 1 − ∑ i = 1 c p i 2 Gini(S)=1-\sum_{i=1}^{c} p_i^2 Gini(S)=1−i=1∑cpi2
分裂时按照基尼系数减少量最大的特征进行分裂
案例------计算信息增益、信息增益率、Gini系数
案例如图:
| 天气 | 温度 | 温度 | 风力 | 打网球 |
|---|---|---|---|---|
| 晴 | 热 | 高 | 弱 | 否 |
| 晴 | 热 | 高 | 强 | 否 |
| 阴 | 热 | 高 | 弱 | 是 |
| 雨 | 适中 | 高 | 弱 | 是 |
| 雨 | 冷 | 正常 | 弱 | 是 |
| 雨 | 冷 | 正常 | 强 | 否 |
| 阴 | 冷 | 正常 | 强 | 是 |
| 晴 | 适中 | 高 | 弱 | 否 |
| 晴 | 冷 | 正常 | 弱 | 是 |
| 雨 | 适中 | 正常 | 弱 | 是 |
| 晴 | 适中 | 正常 | 强 | 是 |
| 阴 | 适中 | 高 | 强 | 是 |
| 阴 | 热 | 正常 | 弱 | 是 |
| 雨 | 适中 | 高 | 强 | 否 |
1.计算信息增益
步骤1:计算整个数据集的熵 H ( S ) H(S) H(S)
总样本数: 14 14 14个
"是"(打网球): 9 9 9个 9 14 \dfrac9{14} 149
"否"(不打网球): 5 5 5个 5 14 \dfrac5{14} 145
则信息熵为:
H ( S ) = − ( 9 14 l o g 2 9 14 + 5 14 l o g 2 5 14 ) = 0.940 H(S)=-(\dfrac{9}{14}\mathrm{log_2}\dfrac9{14}+\dfrac{5}{14}\mathrm{log_2}\dfrac5{14})=0.940 H(S)=−(149log2149+145log2145)=0.940
步骤2:计算按"天气"分裂后的加权平均熵 H ( S ∣ 天气 ) H(S|天气) H(S∣天气)
"晴": 3 3 3天不打网球, 2 2 2天打网球;
"阴": 4 4 4天均打网球;
"雨": 2 2 2天不打网球, 3 3 3天打网球.
H ( S ∣ 天气 = 晴 ) = − ( 2 5 l o g 2 2 5 + 3 5 l o g 2 3 5 ) = 0.971 H(S|天气=晴)=-(\dfrac25\mathrm{log_2}\dfrac25+\dfrac35\mathrm{log_2}\dfrac35)=0.971 H(S∣天气=晴)=−(52log252+53log253)=0.971
H ( S ∣ 天气 = 雨 ) = − ( 2 5 l o g 2 2 5 + 3 5 l o g 2 3 5 ) = 0.971 H(S|天气=雨)=-(\dfrac25\mathrm{log_2}\dfrac25+\dfrac35\mathrm{log_2}\dfrac35)=0.971 H(S∣天气=雨)=−(52log252+53log253)=0.971
H ( S ∣ 天气 = 阴 ) = − ( 4 4 l o g 2 4 4 ) = 0 H(S|天气=阴)=-(\dfrac44\mathrm{log_2}\dfrac44)=0 H(S∣天气=阴)=−(44log244)=0
所以加权平均熵:
5 14 × 0.971 + 5 14 × 0.971 + 4 14 × 0 = 0.694 \dfrac5{14}\times 0.971 +\dfrac5{14}\times 0.971 +\dfrac4{14}\times 0 = 0.694 145×0.971+145×0.971+144×0=0.694
信息增益:
I G ( S , 天气 ) = H ( S ) − H ( S ∣ 天气 ) = 0.940 − 0.694 = 0.246 IG(S,天气)=H(S)-H(S|天气)=0.940-0.694=0.246 IG(S,天气)=H(S)−H(S∣天气)=0.940−0.694=0.246
同理,可以计算其他特征的信息增益如下:
各特征的信息增益:
天气: 0.2467 0.2467 0.2467
温度: 0.0292 0.0292 0.0292
湿度: 0.1518 0.1518 0.1518
风力: 0.0481 0.0481 0.0481
所以按照信息增益最大的方向进行分裂,应该优先按照"天气"特征进行决策树分裂。
上述信息增益的计算也可以使用Python代码实现:
python
import pandas as pd
import numpy as np
from math import log2
# 创建数据
data = {
'天气': ['晴','晴','阴','雨','雨','雨','阴','晴','晴','雨','晴','阴','阴','雨'],
'温度': ['热','热','热','适中','冷','冷','冷','适中','冷','适中','适中','适中','热','适中'],
'湿度': ['高','高','高','高','正常','正常','正常','高','正常','正常','正常','高','正常','高'],
'风力': ['弱','强','弱','弱','弱','强','强','弱','弱','弱','强','强','弱','强'],
'打网球': ['否','否','是','是','是','否','是','否','是','是','是','是','是','否']
}
df = pd.DataFrame(data)
def entropy(labels):
"""计算熵"""
total = len(labels)
if total == 0:
return 0
value_counts = labels.value_counts()
entropy_val = 0
for count in value_counts:
p = count / total
entropy_val -= p * log2(p)
return entropy_val
def information_gain(data, feature, target):
"""计算信息增益"""
# 总熵
total_entropy = entropy(data[target])
# 加权平均熵
weighted_entropy = 0
for value in data[feature].unique():
subset = data[data[feature] == value]
weight = len(subset) / len(data)
weighted_entropy += weight * entropy(subset[target])
# 信息增益
return total_entropy - weighted_entropy
# 计算各特征的信息增益
target = '打网球'
features = ['天气', '温度', '湿度', '风力']
print("各特征的信息增益:")
for feature in features:
ig = information_gain(df, feature, target)
print(f"{feature}: {ig:.4f}")输出如下:
bash
各特征的信息增益:
天气: 0.2467
温度: 0.0292
湿度: 0.1518
风力: 0.04812.计算信息增益率
为了解决信息增益偏好多值特征的问题,所以引入信息增益率。以"天气"特征为例。计算原始数据集S在"天气"特征下的熵
I V ( 天气 ) = − ( 5 14 l o g 2 5 14 + 4 14 l o g 2 4 14 + 5 14 l o g 2 5 14 ) ≈ 1.577 IV(天气)=-(\dfrac{5}{14}\mathrm{log_2}\dfrac{5}{14}+\dfrac{4}{14}\mathrm{log_2}\dfrac{4}{14}+\dfrac{5}{14}\mathrm{log_2}\dfrac{5}{14})\approx1.577 IV(天气)=−(145log2145+144log2144+145log2145)≈1.577
所以信息增益率:
G a i n R a t i o ( 天气 ) = I G ( S ∣ 天气 ) I V ( 天气 ) = 0.2467 1.577 ≈ 0.156 GainRatio(天气)=\dfrac{IG(S|天气)}{IV(天气)}=\dfrac{0.2467}{1.577}\approx0.156 GainRatio(天气)=IV(天气)IG(S∣天气)=1.5770.2467≈0.156
3.基尼系数
(1)计算整个数据集的基尼系数:
总样本数: 14 14 14个
"是"(打网球): 9 9 9个 9 14 \dfrac9{14} 149
"否"(不打网球): 5 5 5个 5 14 \dfrac5{14} 145
G i n i ( S ) = 1 − [ ( 9 14 ) 2 + ( 5 14 ) 2 ] = 90 196 ≈ 0.459 Gini(S)=1-[(\dfrac9{14})^2+(\dfrac{5}{14})^2]=\dfrac{90}{196}\approx0.459 Gini(S)=1−[(149)2+(145)2]=19690≈0.459
(2)计算"天气"特征的加权平均基尼系数
G i n i ( S ∣ 天气 = 晴 ) = 1 − [ ( 2 5 ) 2 + ( 3 5 ) 2 ] = 12 25 = 0.48 Gini(S|天气=晴)=1-[(\dfrac2{5})^2+(\dfrac{3}{5})^2]=\dfrac{12}{25}=0.48 Gini(S∣天气=晴)=1−[(52)2+(53)2]=2512=0.48
G i n i ( S ∣ 天气 = 阴 ) = 1 − [ ( 4 4 ) 2 ] = 0 Gini(S|天气=阴)=1-[(\dfrac4{4})^2]=0 Gini(S∣天气=阴)=1−[(44)2]=0
G i n i ( S ∣ 天气 = 雨 ) = 1 − [ ( 2 5 ) 2 + ( 3 5 ) 2 ] = 12 25 = 0.48 Gini(S|天气=雨)=1-[(\dfrac2{5})^2+(\dfrac{3}{5})^2]=\dfrac{12}{25}=0.48 Gini(S∣天气=雨)=1−[(52)2+(53)2]=2512=0.48
G i n i ( S ∣ 天气 ) = 5 14 × 0.48 + 5 14 × 0.48 + 4 14 × 0 ≈ 0.343 Gini(S|天气)=\dfrac{5}{14}\times 0.48+ \dfrac{5}{14}\times 0.48+\dfrac4{14}\times 0\approx0.343 Gini(S∣天气)=145×0.48+145×0.48+144×0≈0.343
(3)计算基尼系数减少量
Δ G i n i ( S ) = G i n i ( S ) − G i n i ( S ∣ 天气 ) = 0.459 − 0.343 = 0.116 \Delta Gini(S)=Gini(S)-Gini(S|天气)=0.459-0.343=0.116 ΔGini(S)=Gini(S)−Gini(S∣天气)=0.459−0.343=0.116
上述信息增益率和基尼系数也可以使用以下代码计算:
python
import pandas as pd
import numpy as np
from math import log2
# 数据
data = {
'天气': ['晴','晴','阴','雨','雨','雨','阴','晴','晴','雨','晴','阴','阴','雨'],
'温度': ['热','热','热','适中','冷','冷','冷','适中','冷','适中','适中','适中','热','适中'],
'湿度': ['高','高','高','高','正常','正常','正常','高','正常','正常','正常','高','正常','高'],
'风力': ['弱','强','弱','弱','弱','强','强','弱','弱','弱','强','强','弱','强'],
'打网球': ['否','否','是','是','是','否','是','否','是','是','是','是','是','否']
}
df = pd.DataFrame(data)
def entropy(labels):
"""计算熵"""
total = len(labels)
if total == 0:
return 0
value_counts = labels.value_counts()
entropy_val = 0
for count in value_counts:
p = count / total
if p > 0:
entropy_val -= p * log2(p)
return entropy_val
def gini(labels):
"""计算基尼系数"""
total = len(labels)
if total == 0:
return 0
value_counts = labels.value_counts()
gini_val = 1
for count in value_counts:
p = count / total
gini_val -= p ** 2
return gini_val
def intrinsic_value(data, feature):
"""计算特征的固有值(分裂信息量)"""
total = len(data)
value_counts = data[feature].value_counts()
iv = 0
for count in value_counts:
p = count / total
iv -= p * log2(p)
return iv
def information_gain_ratio(data, feature, target):
"""计算信息增益率"""
# 信息增益
total_entropy = entropy(data[target])
weighted_entropy = 0
for value in data[feature].unique():
subset = data[data[feature] == value]
weight = len(subset) / len(data)
weighted_entropy += weight * entropy(subset[target])
ig = total_entropy - weighted_entropy
# 固有值
iv = intrinsic_value(data, feature)
# 信息增益率
gain_ratio = ig / iv if iv > 0 else 0
return ig, iv, gain_ratio
def gini_reduction(data, feature, target):
"""计算基尼系数减少量"""
# 总基尼系数
total_gini = gini(data[target])
# 加权平均基尼系数
weighted_gini = 0
for value in data[feature].unique():
subset = data[data[feature] == value]
weight = len(subset) / len(data)
weighted_gini += weight * gini(subset[target])
# 基尼系数减少量
gini_reduction = total_gini - weighted_gini
return total_gini, weighted_gini, gini_reduction
# 计算所有特征
target = '打网球'
features = ['天气', '温度', '湿度', '风力']
print("=== 信息增益率分析 ===")
for feature in features:
ig, iv, gr = information_gain_ratio(df, feature, target)
print(f"{feature}: IG={ig:.4f}, IV={iv:.4f}, 增益率={gr:.4f}")
print("\n=== 基尼系数分析 ===")
for feature in features:
gini_total, gini_weighted, gini_red = gini_reduction(df, feature, target)
print(f"{feature}: 总基尼={gini_total:.4f}, 加权基尼={gini_weighted:.4f}, 减少量={gini_red:.4f}")结果如下:
bash
=== 信息增益率分析 ===
天气: IG=0.2467, IV=1.5774, 增益率=0.1564
温度: IG=0.0292, IV=1.5567, 增益率=0.0188
湿度: IG=0.1518, IV=1.0000, 增益率=0.1518
风力: IG=0.0481, IV=0.9852, 增益率=0.0488
=== 基尼系数分析 ===
天气: 总基尼=0.4592, 加权基尼=0.3429, 减少量=0.1163
温度: 总基尼=0.4592, 加权基尼=0.4405, 减少量=0.0187
湿度: 总基尼=0.4592, 加权基尼=0.3673, 减少量=0.0918
风力: 总基尼=0.4592, 加权基尼=0.4286, 减少量=0.0306所以按照信息增益率和基尼系数计算都是按照"天气"特征进行分裂。
决策树的分类与实现
分类
按分裂规则分类
决策树按照上述分裂规则,主要分为以下三类
(1)按照信息增益进行分裂:ID3决策树
(2)按照信息增益率进行分裂:C4.5决策树
(3)按照基尼系数减少量进行分裂:CART决策树(Classification And Regression Tree)
目前,使用最多的是CART决策树,其既可以实现回归任务,也可以进行分类任务。
按任务类型分类
(a)分类任务:每个非叶子结点是一个判断条件,根据判断条件进行if-else分类,最终叶子结点就是所属类别。
(b)回归任务:将数值相近的样本分到同一组,叶子节点内取平均值。
但是一般决策树用作分类模型
实现
使用sklearn实现决策树
python
# 1.决策树进行分类任务
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score,precision_score,confusion_matrix,recall_score
from sklearn.tree import DecisionTreeClassifier
# 1.加载数据集
iris = load_iris()
# 2.数据集分割
X_train,X_test,y_train,y_test = train_test_split(iris.data,iris.target,train_size=0.3,random_state=42,shuffle=True)
# 3.定义决策树分类器
Tree = DecisionTreeClassifier(max_depth=5,min_samples_split=2,min_samples_leaf=1)
# 4.训练
Tree.fit(X_train,y_train)
# 5.预测
y_pred = Tree.predict(X_test).astype('int')
# 6.输出准确率
print(f'准确率为:{accuracy_score(y_test,y_pred):.3f}')
print(f'漏报率(召回率:Recall):{recall_score(y_test,y_pred,average="macro"):.3f}')
print(f'混淆矩阵:\n{confusion_matrix(y_test,y_pred)}')输出如下:
bash
准确率为:0.924
漏报率(召回率:Recall):0.918
混淆矩阵:
[[40 0 0]
[ 0 28 5]
[ 0 3 29]]可视化以及预剪枝
可视化
使用sklearn中tree包内的plot_tree方法,可以实现决策树的可视化:
python
# 7. 决策树可视化
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
plt.figure(figsize=(20, 12))
plot_tree(
Tree,
feature_names=iris.feature_names,
class_names=iris.target_names,
filled=True, # 颜色填充
rounded=True, # 圆角矩形
proportion=True, # 显示样本比例
impurity=False, # 不显示不纯度
fontsize=10
)
plt.show()结果如下:
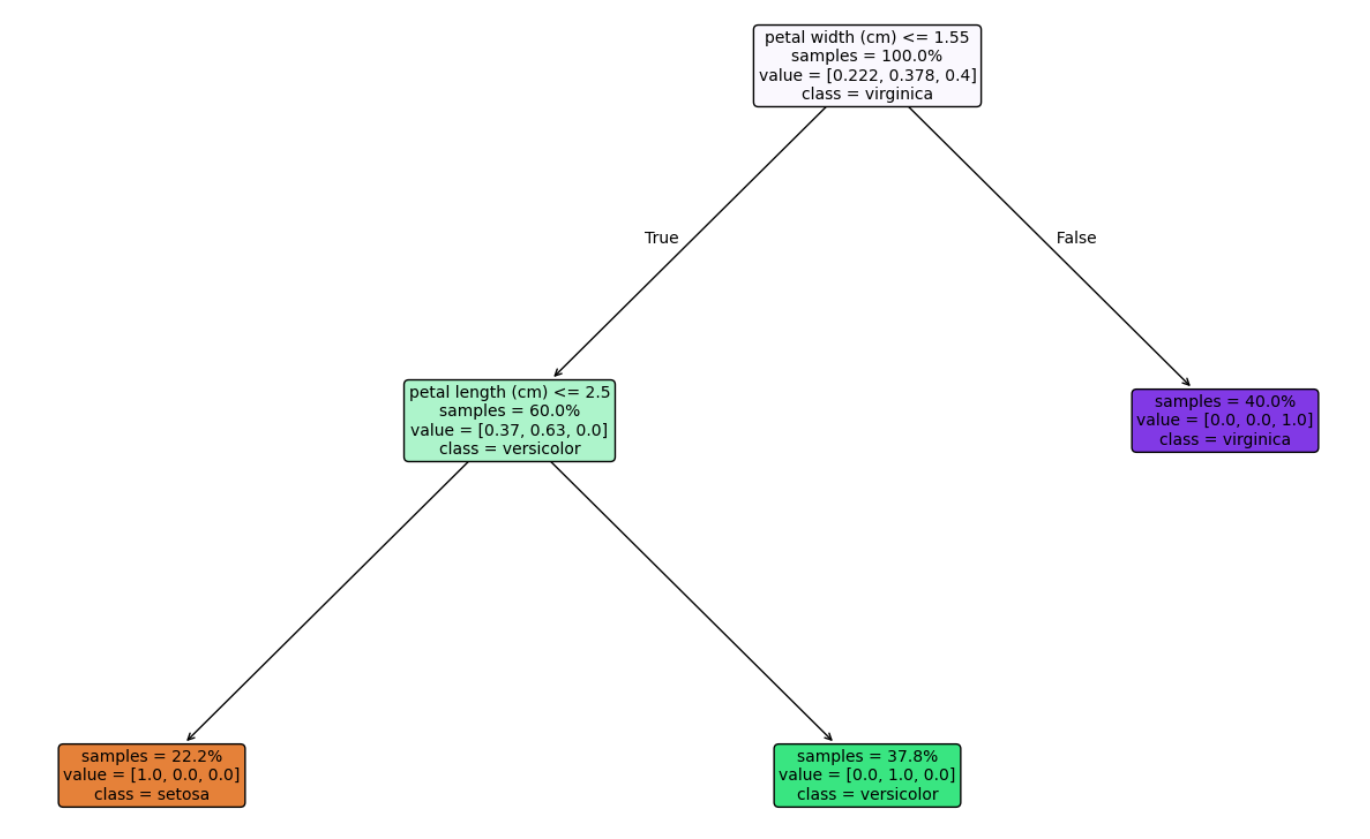
预剪枝
上面的决策树只有三层,其实这主要是在我们定义决策树模型的时候,对参数进行了限制,即进行了预剪枝。防止其过度分裂从而过拟合。
常见的预剪枝参数如下:
| 参数 | 作用 | 推荐范围 |
|---|---|---|
| max_depth | 树的最大深度 | 3-10 |
| min_samples_split | 节点最小分裂样本数 | 2-20 |
| min_samples_leaf | 叶节点最小样本数 | 1-10 |
| max_leaf_nodes | 最大叶节点数量 | 10-100 |
| min_impurity_decrease | 最小不纯度减少量 | 0.0-0.1 |