旋转矩阵的推导:

简单谈谈对矩阵的理解以及在3DGS中的应用:
矩阵本质上是一种线性变换,尤其在计算机图形学(CG)/机器人学等领域。比如将一个坐标系下的点用另一个坐标系表示,这个过程就是涉及到坐标系的转换,通过矩阵能够较方便的完成。
在3DGS中,这个任务本质上是需要不断优化高斯椭球内部的参数,而高斯椭球的内部参数之一就是协方差矩阵Σ。协方差矩阵能够用来表示三维空间中的一个普通椭球,这个其实可以联系到线性代数中的二次型相关知识。
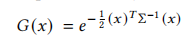
观察3DGS椭球的表示式,左边的G(x)是一种概率分布取指,属于[0,1]之间。当G(x)取某一个具体的值时,就对应着一个Σ,在空间中也就对应着一个椭球壳。所以当G(x)取指非常多时,也就是一系列的概率分布取值,就对应着空间中许多个椭球壳,他们一个套在一个上面,形成了一个实心的椭球体。所以3DGS椭球本质上是"实心"的。
在3DGS的渲染过程中,对于3DGS椭球中的每一个点,他有相对于椭球中心的一个坐标系,也有相机坐标系,投影平面(一般就是屏幕)坐标系等等。整个渲染的过程实际上就是高斯椭球中的点最终如何在投影平面表示的问题。这个转换过程就涉及到非常多的矩阵映射。经过了一个矩阵变换后,用来表示高斯椭球的协方差Σ也就要经过转化。
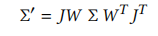
在3DGS中主要有两种矩阵变换,一种是线性的,一种是非线性的。对于线性的变化,变化后的协方差Σ'会和变化前协方差Σ直接相关联,可以通过转化矩阵W推导得到;而对于非线性的变化,则需要使用雅可比矩阵J来近似表示。
当把高斯椭球中的参数Σ在变化的过程中用变化矩阵表示出来之后,那么接下来就是基本的感知器原理,不断通过反向传播优化这一些参数。