旋转矩阵有两种理解方式;
一、姿态描述
描述相机坐标系相对于世界坐标系怎么摆放(即姿态);
其物理意义是:"将一个在相机坐标系中的矢量,变换回世界坐标系",即

设相机坐标系的三个单位基向量在世界坐标系中的表示为:

将它们按列组成矩阵:
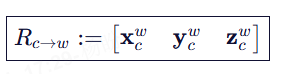
这个矩阵的含义是:把相机坐标系中的一个向量(以相机基底表示),主动旋转到世界坐标系中。例如,相机中的单位向量 (1,0,0)⊤(即其 X 轴)在世界中就是:
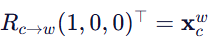
因此,Rc→w 被称为相机到世界的姿态矩阵(或方向余弦矩阵)。
二、坐标变换
将同一个点在世界坐标系下的坐标Pw变换到相机坐标系下的坐标Pc 。这由坐标变换矩阵实现:
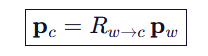
其中 Rw→c∈SO(3) 是世界到相机的坐标变换矩阵。
从上面的定义描述可以看出,姿态描述和坐标变换(世界点到相机点)是互为转置。
仅仅看上面两个信息可能没什么概念,下面举一个实例,信息如下:
1.车辆前挡风玻璃上端一个,朝前,称之为前视相机,后挡风玻璃上端一个,朝后,称之为后视相机。 左右各两个,左边一个朝左前、一个朝左后,分别称之为左前相机和左后相机。右边一个朝右前、一个朝右后,分别称之为右前相机和右后相机。
2.前视pyr角度分别为5°,0°,0°,后视pyr角度分别为5°,180°,0 °。左前pyr角度分别为0°,45°,0°,右前pyr角度分别为0°,-45°,0° 。左后pyr角度分别为0°,135°,0°。右后pyr角度分别为0°,-145°,0 °.
3.相机坐标系和世界坐标系均为前左上。
求相机的姿态和世界坐标系到相机坐标系的旋转矩阵Rwc 。
以左前相机为例,rx = 0,ry = 0°,rz = 45°. 根据欧拉角转旋转矩阵定义,按照XYZ的旋转顺序,外旋得到R, R = Rz(yaw)Ry(pitch)Rx(roll) .
那么问题来了,这个R是相机的姿态(Rcw),还是Rwc 。
- 要求上面的两个问题,先确认上面的角度值是哪个坐标系到哪个坐标系的旋转。
根据上面的角度正负号,结合右手定则,可以确认,上面的旋转是世界坐标系到相机坐标系的旋转得到。
2.求相机的姿态、及Rwc。
下面参考博客:https://blog.csdn.net/weixin_45632220/article/details/117735223 中的推导,及上面的定义来给出答案。
首先根据第一节中姿态描述的物理含义:"将一个在相机坐标系中的矢量,变换回世界坐标系" 。
结合参考文献中的"坐标变换"部分的推导,如下。红色坐标系可以类比我们的相机坐标系,黑色坐标系可以类比我们的世界坐标系。
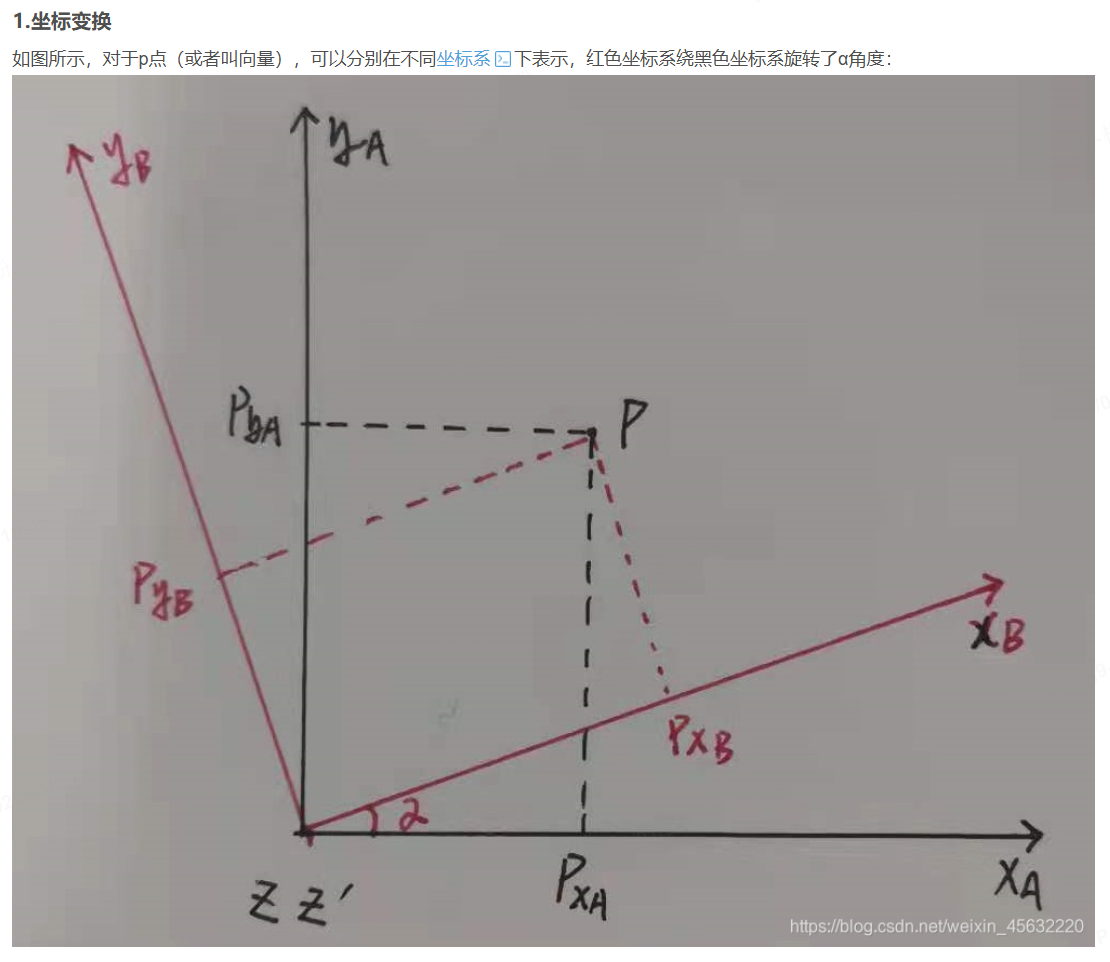

上面的推导,正好和左前相机角度转换类似,只绕Z轴旋转了α ,假设α = 45°。我们就可以通过R = Rz(yaw)Ry(pitch)Rx(roll) 将相机坐标系下的点,投影到世界坐标系。也就是说,Rz(yaw)Ry(pitch)Rx(roll) = Rcw 。
那Rwc = (Rz(yaw)Ry(pitch)Rx(roll)).inv() 。