三维重建【7】Grendel-GS：ON SCALING UP 3D GAUSSIAN SPLATTING TRAINING

三维重建【7】Grendel-GS：ON SCALING UP 3D GAUSSIAN SPLATTING TRAINING

• 一、摘要
• • [1. 原文](#1. 原文)
  • [2. 译文](#2. 译文)
• 二、前言
• 三、高斯泼溅：背景、机遇和挑战
• • [3.1 3D Gaussian训练的背景](#3.1 3D Gaussian训练的背景)
  • [3.2 3DGS分布式化中的机遇与挑战](#3.2 3DGS分布式化中的机遇与挑战)
• 四、系统设计
• • [4.1 混合并行训练](#4.1 混合并行训练)
  • [4.2 迭代工作负载重新平衡](#4.2 迭代工作负载重新平衡)
• 五、缩放超参数以进行批量训练
• • [5.1 独立梯度的经验证据](#5.1 独立梯度的经验证据)
  • [5.2 所提出缩放规则的实验验证](#5.2 所提出缩放规则的实验验证)

一、摘要

1. 原文

3D Gaussian Splatting (3DGS) is increasingly popular for 3D reconstruction due to its superior visual quality and rendering speed. However, 3DGS training currently occurs on a single GPU, limiting its ability to handle high-resolution and large-scale 3D reconstruction tasks due to memory constraints. We introduce Grendel, a distributed system designed to partition 3DGS parameters and parallelize computation across multiple GPUs. As each Gaussian affects a small, dynamic subset of rendered pixels, Grendel employs sparse all-to-all communication to transfer the necessary Gaussians to pixel partitions and performs dynamic load balancing. Unlike existing 3DGS systems that train using one camera view image at a time, Grendel supports batched training with multiple views. We explore various optimization hyperparameter scaling strategies and find that a simple sqrt(batch_size) scaling rule is highly effective. Evaluations using large-scale, high-resolution scenes show that Grendel enhances rendering quality by scaling up 3DGS parameters across multiple GPUs. On the 4K "Rubble" dataset, we achieve a test PSNR of 27.28 by distributing 40.4 million Gaussians across 16 GPUs, compared to a PSNR of 26.28 using 11.2 million Gaussians on a single GPU. Grendel is an open-source project available at: https://github.com/ nyu-systems/Grendel-GS.

2. 译文

3D高斯泼溅 (3DGS) 由于其卓越的视觉质量和渲染速度而在三维重建中越来越受欢迎。然而，3DGS 训练目前在单个 GPU 上进行，由于内存限制，限制了其处理高分辨率和大规模三维重建任务的能力。我们引入了 Grendel，这是一个分布式系统，旨在划分 3DGS 参数并跨多个 GPU 并行计算。由于每个高斯影响渲染像素的一个小的动态子集，Grendel 采用稀疏的全对所有通信将必要的高斯传输到像素分区并执行动态负载平衡。与一次使用一张相机视图图像进行训练的现有 3DGS 系统不同，Grendel 支持使用多个视图进行批量训练。我们探索了各种优化超参数缩放策略，发现简单的 sqrt(batch_size) 缩放规则非常有效。使用大规模、高分辨率场景的评估表明，Grendel 通过跨多个 GPU 扩展 3DGS 参数来提高渲染质量。在 4K"Rubble"数据集上，我们通过在 16 个 GPU 上分配 4040 万个高斯函数，实现了 27.28 的测试 PSNR，而在单个 GPU 上使用 1120 万个高斯函数时，测试 PSNR 为 26.28。 Grendel 是一个开源项目，网址为：https://github.com/nyu-systems/Grendel-GS。

二、前言

3D Gaussian Splatting（3DGS）已成为 3D 新颖视图合成的流行技术，主要是因为与 NeRF等以前的方法相比，它的训练和渲染速度更快。然而，大多数现有的3DGS流程仅限于使用单个 GPU 进行训练，在应用于高分辨率或较大规模的场景时会产生内存和计算瓶颈。例如，标准 Rubble 数据集包含 1657 张图像，每张图像的分辨率为 4K。单个 A100 40GB GPU 最多可容纳 1120 万高斯------远低于 3DGS 的质量饱和点。正如我们在第 5.2.1 节中所演示的，增加高斯数量可以继续提高重建质量。因此，为了在参数数量和速度方面扩展 3DGS 训练，我们开发了 Grendel 系统，该系统将 3DGS 训练分布在多个 GPU 上，并使用经验规则根据批量大小自动调整训练超参数。

将 3DGS 扩展到大规模场景的现有工作已经探索了诸如分而治之、细节层次表示和渲染的方法。这些方法是对系统级并行化方法的补充，我们采用系统级并行化方法来扩展 3DGS，超越单个 GPU 的内存和计算限制。

由于分布式训练框架已广泛用于许多最先进的 DNN 模型，例如 LLM，因此也很容易使用它们来分发 3DGS。然而，虽然 3DGS 使用基于梯度的优化，但它并不是基于神经网络。具体来说，它具有独特的计算管道，具有动态和不平衡的工作负载模式。现有的 DNN 训练框架假设工作负载与常规密集张量操作一致且平衡，因此不适用于 3DGS。

在本文中，我们提出了若干关于 3DGS 扩展训练（scaling up） 的关键观察，这些观察为我们设计分布式训练流水线提供了重要依据。例如，我们发现，在一次迭代中，3DGS 训练流水线的每一个阶段都可以被有效地并行化，但不同阶段所采用的并行化维度并不相同，从而形成了混合并行**（mixed parallelism）。更具体地说，在 3DGS 中，有些计算是针对单个输出像素进行的（因此可以进行 像素级并行**），而另一些计算则是针对单个三维高斯体进行的（因此可以进行高斯体级并行 ）。这种混合并行方式使得不同阶段之间需要进行数据重排与传递。为了减少通信开销，我们进一步观察到，3DGS 具有明显的空间局部性 ：在渲染某一个输出图像块时，通常只有少量的高斯体会对其产生影响。最后，我们还发现，随着训练过程的推进，渲染单个输出像素的计算强度会不断变化。这种动态且负载不均衡的计算特性会导致任何静态的工作负载划分策略随着时间推移逐渐变得不再最优。

在本文中，我们描述了 Grendel，一个分布式 3DGS 训练框架，旨在利用我们的上述观察结果。 Grendel 在训练迭代中的步骤中使用高斯分布（即，它在 GPU 上分布高斯），这些步骤表现出高斯并行性，而其他步骤则采用像素分布。它通过在像素级分布期间将连续图像区域分配给 GPU 并利用空间局部性来最小化在 GPU 之间传输的高斯数量，从而最大限度地减少在高斯级分布和像素级分布之间切换时的通信开销。最后，Grendel 采用动态负载平衡器，该负载平衡器使用先前的训练迭代来分配像素级计算，以最大限度地减少工作负载不平衡。

Grendel 还通过批量处理多个图像来扩大训练规模。这与传统的 3DGS 训练不同，传统的 3DGS 训练仅使用批量大小 1，这会导致分布式框架中 GPU 利用率的降低。为了保持较大批次的数据效率和重建质量，需要重新调整优化器超参数。为此，我们基于启发式独立梯度假设，引入了用于批量 3DGS 训练的自动超参数缩放规则。我们凭经验验证了我们提出的方法的有效性Grendel 支持大批量（我们测试最多 32 个）的分布式训练，同时与批量大小 = 1 相比保持重建质量和数据效率。

总而言之，本文的工作做了以下贡献：

• 我们描述了 Grendel 的设计和实现，Grendel 是一个可扩展、内存高效、自适应的 3DGS 分布式训练系统。 Grendel 允许批量 3DGS 训练扩展并在多达 32 个 GPU 上运行。
• 我们探索 3DGS 的大批量训练动态，以确定一种简单的 sqrt(batch_size) 学习率缩放策略，该策略可以针对超过 1 的批量大小实现高效、无需超参数调整的训练。
• 我们展示了 Grendel 支持高分辨率大规模场景渲染：我们使用 16 个 GPU 并为来自 MegaNERF 的大规模 Rubble 场景渲染 4K 图像。对于这个场景，Grendel 使用 4040 万个高斯函数实现了 27.28 的 PSNR，超越了当前的最先进水平。所需的内存超出了单个 GPU 的容量，因此如果没有 Grendel 的技术，很难以这种质量渲染该场景。

理解： 3DGS的训练虽然可以并行加速，但"不同步骤适合用不同的并行方式"，而且计算量会随时间变化，所以不能用一种固定的分工方式一致算下去，必须设计更灵活、更聪明的分布式训练方案。

三、高斯泼溅：背景、机遇和挑战

3D Gaussian Splatting（3DGS）是一种使用一组（可能很大）各向异性 3D 高斯函数来表示 3D 场景的渲染方法。每个 3D 高斯分布由四个可学习参数表示： 1) 其 3D 位置 x i ∈ R 3 x_i∈ \mathbb{R}^3 xi∈R3； 2) 其形状由使用高斯缩放向量 s i ∈ R 3 s_i∈ \mathbb{R}^3 si∈R3和旋转向量 q i ∈ R 4 q_i∈ \mathbb{R}^4 qi∈R4计算的 3D 协方差矩阵描述； 3) 其不透明度 α i ∈ R \alpha_i∈ \mathbb{R} αi∈R； 4) 其球谐函数 s h i ∈ R 48 sh_i∈ \mathbb{R}^{48} shi∈R48。每个高斯的颜色贡献由这些参数和观察方向决定。

3.1 3D Gaussian训练的背景

为了训练 3DGS，用户提供场景的初始点云（可以是随机的或估计的）和一组来自不同角度的姿势图像。训练过程使用点云初始化高斯。每个训练步骤都会选择一个随机相机视图，并使用当前的高斯参数来渲染视图。然后，它通过将渲染图像与地面实况进行比较来计算损失，并使用反向传播来更新高斯参数。训练过程还使用自适应致密化机制，通过根据位置方差和尺度阈值克隆或分割现有高斯函数，将高斯函数添加到重建区域中。 具体来说，训练流程由四个步骤组成：高斯变换、图像渲染、损失计算和反向传播。在此设置中使用反向传播的标准方法，我们详细介绍了下面的其余三个步骤：

• 高斯变换： 给定一个相机视角 v v v及其对应的屏幕空间，每一个高斯体 i i i都会被变换并投影到屏幕上，从而确定其在屏幕空间中的二维位置 x v , i ∈ R 2 x_{v,i} \in \mathbb{R}^2 xv,i∈R2、其相对于屏幕的深度 d e p t h v , i ∈ R {depth}{v,i} \in \mathbb{R} depthv,i∈R、其覆盖范围（或投影后的足迹半径） r a d i u s v , i ∈ R {radius}{v,i} \in \mathbb{R} radiusv,i∈R，此外高斯体在该视角下的颜色 c v , i c_{v,i} cv,i会根据观察方向通过其可学习的球谐系数 s h i ∈ R 4 8 {sh}_{i} \in \mathbb{R}^48 shi∈R48进行计算得到。
• 渲染： 在完成高斯变换之后，通过计算每个像素的颜色来生成最终图像。对于给定的像素 p p p，3DGS首先找出所有与该像素相交的高斯体。若像素 p p p位于高斯体 i i i投影中心 x v , i x_{v,i} xv,i的半径 d e p t h v , i {depth}{v,i} depthv,i范围之内，则认为该高斯体与像素 p p p相交。随后，3DGS按照深度从近到远（即 d e p t h v , i {depth}{v,i} depthv,i递增的顺序）遍历所有相交的高斯体，并通过 α \alpha α合成累加它们对该像素的贡献，直到不透明度达到预设阈值为止。
• 损失计算： 最后。3DGS通过将渲染得到的图像与真实图像进行对比，计算L1损失和SSIM损失。L1损失用于衡量像素颜色之间的绝对差异，SSIM损失用于衡量局部像素窗口之间的结构相似性。这两种损失都会以逐像素的方式计算，并同时用于前向与反向传播过程。

3.2 3DGS分布式化中的机遇与挑战

在设计用于扩展 3D 高斯泼溅训练的 Grendel 时，我们在上述训练过程中利用了以下机遇并解决了几个挑战：

• 机遇：混合并行。 上述每个步骤本质上都具备并行性，但需要不同的工作划分方式。具体来说，高斯变换步骤以单个高斯为处理对象，因此应按高斯进行划分；而渲染与损失计算步骤以单个像素（或用于SSIM损失的像素窗口）为处理对象，因此应按像素进行划分。
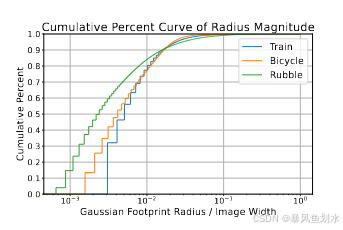
• 机遇：空间局部性。 由于高斯通常具有较小的半径，大多数高斯只会与渲染图像中的一小块连续区域相交。如下图所示，在三个场景中，90%的3D高斯的半径小于图像宽度的2%。因此，一个像素只会受到场景中的一小部分3D高斯的影响，并且相邻像素所对应的高斯集合之间存在显著重叠。
  
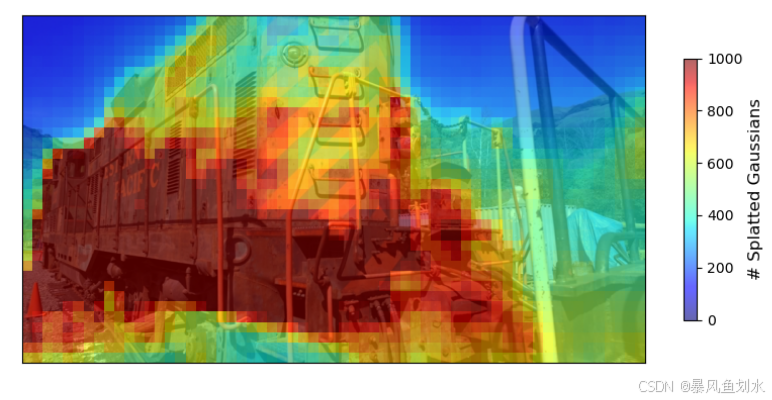
• 挑战：动态且负载不均衡的工作量。 不同图像区域相交的高斯数量差异很大，如下图所示。例如，包含天空的图像区域往往对应较少的高斯，而包含人物的区域则可能对应更多高斯。此外，高斯的密度、位置、形状与不透明度会在训练过程中不断变化。因此，高斯数量及其到像素的映射关系会随时间演化，导致不同图像区域之间以及训练不同时期的计算负载不均衡。固定的划分方案因此会遭遇负载失衡问题。
• 
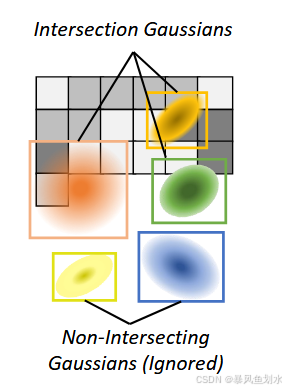
• 挑战：缺乏批处理。 当前3DGS系统一次只处理一张图像，这在单GPU训练中已足够。然而，如下图所示，在多GPU的分布式场景下，这种方式效率较低。要通过更大的批大小实现高效训练，需要理解3DGS独特的优化动力学特性，而这些特性可能不同于传统神经网络。
  

四、系统设计

接下来，我们将描述Grendel如何利用3DGS的混合并行和空间局部性来应对动态和不平衡工作负载的挑战。

4.1 混合并行训练

如下图所示是Grendel的结构图。Grendel按照3DGS的混合并行性分配工作：在高斯变换阶段采用按高斯体分配------每个 GPU处理一组互不重叠的高斯体子集；在图像渲染与损失计算阶段采用按像素分配------每个GPU处理一组互不重叠的像素子集。由于3DGS具有空间局部性特征，Grendel在这两个阶段切换时可以从稀疏all-to-all中获益。

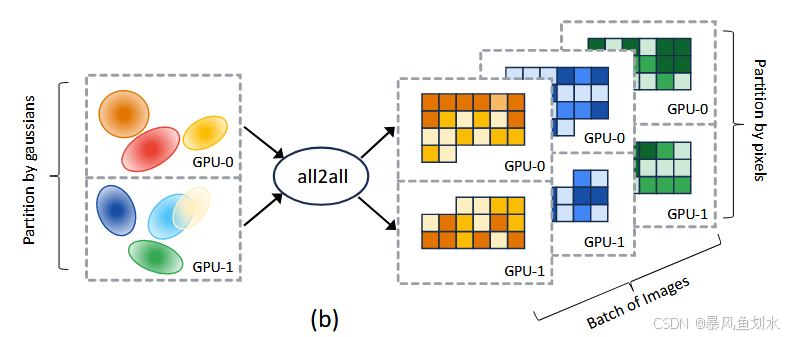
按高斯体分配。 Grendel将高斯体（包括参数以及优化器状态）进行划分，并在各个GPU之间均匀分配。随后，每个GPU独立地对分配到的那部分3D高斯体计算高斯变换。我们发现，不同高斯体所需的计算量差异并不显著，因此将高斯体在GPU间均匀分配，既能在显存约束下容纳尽可能多的高斯体，又能让该步骤的计算随GPU数量近似线性加速。

按像素分配。 在图像渲染与损失计算步骤中，我们将图像中连续的区域分配给不同GPU。分配连续区域有助于利用空间局部性，并减少GPU之间需要传输的高斯体数量。在我们的实现中，我们将一个batch中的每张图像划分为16×16像素块，对这些块进行序列化，然后采用一种自适应策略，把连续的块子序列分配给不同GPU。为了支持批处理，每个GPU可以同时被分配来自同一batch中不同图像的块。

利用稀疏all-to-all通信传输高斯体。 为了渲染某个图像像素，GPU需要访问与该像素相交的高斯体；但这些相交关系与视角相关，并且会在训练过程中变化，因此无法预先确定。为此，Grendel在高斯变换之后加入了一个通信步骤。由于3DGS具有空间局部性，每个像素分区通常只需要3D高斯体的一小部分。我们利用这一点来减少通信：每个GPU会先确定其负责渲染的像素分区所需的相交高斯体集合，再通过稀疏all-to-all通信拉取与该分区任意相交的高斯体。在反向传播阶段，还会执行一次相反方向的all-to-all通信。

尽管Grendel的涉及与用于分布式神经网络训练的FSDP有一些相似之处，但也存在重要的区别。首先，与FSDP中的权重分片不同，Grendel中的高斯分布不仅用于存储，还用于计算（高斯变换）。其次，与使用密集全收集通信传输权重分片的FSDP不同，Grendel使用稀疏全收集通信仅传输相关的高斯分布。

先按高斯体并行把"高斯投影"算完，再按像素并行做"渲染+损失"，中间通过空间局部性做稀疏all-to-all，只把某个像素区域真正需要的高斯体传过去。

4.2 迭代工作负载重新平衡

按像素分配的再均衡。 渲染一个像素的计算负载会随空间（不同像素位置）和时间（不同训练迭代）而变化。因此，不同于分布式神经网络训练中常见的情况，采用均匀或固定的划分方式并不能保证各GPU负载均衡，需要一种自适应的像素分配策略。

我们在训练的前几个epoch之后，于每个epoch记录每张训练图像中每个像素的渲染时间。由于训练过程中场景在相邻epoch之间通常变化平滑，每个像素的渲染时间也会缓慢变化。因此，前几个epoch的渲染时间可以很好地估计当前epoch中该像素的渲染时间。基于这一估计，我们可以自适应地将像素分配到不同GPU，使各GPU的工作量大致均衡。

具体而言，Grendel会测量分配给某个GPU的每个像素块的运行时间（包括图像渲染、损失计算以及相应的反向计算），计算该GPU的平均单像素计算时间，并用该平均值来近似该GPU上任意像素 p p p的计算时间。举例来说，若某GPU被分配了像素 p 0 p_0 p0到 p n p_n pn，并用时 t t t完成这些像素的计算，则Grendel假设对于任意 𝑖∈[0,𝑛]，像素 p i p_i pi的计算时间约为 t / n t/n t/n。在后续迭代中，系统会重新划分图像，使分配给各 GPU 的像素计算时间总和尽量相等。在我们的实现中，划分粒度采用 16×16 像素块。我们给出了用于计算划分点、将图像切分为负载均衡的块子序列的伪代码。

本段伪代码的作用是： 根据每个像素块的预计渲染耗时，把一张图像（序列化后的B个块）切成G段连续子序列，让每段的"预计总耗时"尽量相等，从而实现按像素分配的负载均衡。
输入： 像素块数量B，GPU数量G， E N j EN_j ENj表示第 j j j个像素块的预计运行时间
输出： DP切分点，本质是一些索引位置，用来把块序列切成G段

逐行解释：

第一行：计算前缀和（累计耗时）

第二行： C T [ B − 1 ] CT[B-1] CT[B−1]是全部B个块的总预计耗时，除以G得到每张GPU理想承担的目标耗时

第三行：构造阈值数组（每个切分点应该达到的累计耗时位置）

第四行：searchsorted(CT, TH) 会对每个阈值 TH[i]，找到 CT 中第一个满足 CT[idx] >= TH[i] 的位置 idx

第五行：返回切分点数组DP

按高斯体分配的再均衡。 在训练开始时，我们将 3D 高斯体在各 GPU 之间均匀分配。随着训练推进，会通过克隆和拆分现有高斯体来添加新的高斯体。新增高斯体会导致分配失衡，因为不同高斯体的致密化（densify）速率取决于场景局部细节，因而可能差异很大。因此，我们在每经过若干次致密化步骤后会重新分配 3D 高斯体，以恢复均匀性。

五、缩放超参数以进行批量训练

为了有效地扩展到多个GPU，Grendel将批量大小的增加到超过1，从而能够对图像和每个图像内的像素进行分区。

然而，在不调整超参数（尤其是学习率）的情况下增加批量大小可能会导致训练不稳定且效率低下，并且超参数调整通常很乏味。尽管某些方法简化了深度神经网络的学习率调整，但它们要么建立在SGD的基础上（我们使用Adam），要么利用神经网络的分层结构（3DGS不是神经网络）。我们的结果是由3DGS训练的独立梯度假设驱动的。受 Malladi 等人（2022）的启发，我们推导了 Adam 优化器超参数的尺度缩放规则。该分析在学习率的缩放方式上与已有工作一致（Malladi et al., 2022；Granziol et al., 2022），但为 β₁ 和 β₂ 提出了不同的缩放策略，并且在 3DGS 任务中表现更优。

我们提出根据批大小对Adam优化器的学习率和动量参数进行如下缩放：
λ ′ = λ × batch_size β 1 ′ , β 2 ′ = β 1 batch_size , β 2 batch_size \begin{align} \lambda' &= \lambda \times \sqrt{\text{batch\_size}} \\ \beta_1', \beta_2' &= \beta_1^{\text{batch\_size}}, \beta_2^{\text{batch\_size}} \end{align} λ′β1′,β2′=λ×batch_size =β1batch_size,β2batch_size

其中，λ 为原始学习率，β₁ 和 β₂ 分别是 Adam 中一阶矩和二阶矩的原始参数；λ′、β′₁ 和 β′₂ 是为适应更大批大小而调整后的超参数。我们将上述规则分别称为平方根学习率缩放规则 和指数动量缩放规则。

独立梯度假设。 为了推导这些缩放规则，我们首先在一个简化的设定下分析3DGS的训练过程，假设从每个相机视角计算得到的梯度彼此独立，与其它视角诱导的梯度无关。因此，给定一个包含𝑏个相机视角的批次，对批次中每个视角分别执行𝑏次顺序的梯度下降更新，等价于执行一次更大的更新，其中梯度被累加在一起。如果使用的是标准的梯度下降算法，并对一个批次内的梯度取平均，那么将学习率按批大小进行线性缩放即可实现这种等价性。然而，3DGS采用的是Adam这一自适应学习率优化器，其特点在于：(1) 会将梯度除以每个参数对应的二阶矩估计的平方根；(2) 通过指数滑动平均的方式利用动量，将当前梯度与历史梯度进行融合。这使得一次较大的更新并不等同于简单地累加多次小批大小更新。在独立梯度假设下，我们推导了如下对 Adam 超参数的修正方式，以在使用更大批大小时近似批大小为 1 的训练行为：

我们将(g_k)记为在视角k下某参数的梯度，将 g = ∑ j ∈ V g j ∣ V ∣ g = \frac{\sum_{j \in V} g_j}{|V|} g=∣V∣∑j∈Vgj记为全批次梯度（所有视角梯度的均值），其中V是所有视角的集合。我们进一步假设对所有k都有 E [ g k ] = 0 \mathbb{E}[g_k] = 0 E[gk]=0。根据独立性假设：当 k ≠ j k \neq j k=j时， Cov ( g k , g j ) = E [ ( g k − 0 ) ( g j − 0 ) ] = 0 \text{Cov}(g_k, g_j) = \mathbb{E}[(g_k - 0)(g_j - 0)] = 0 Cov(gk,gj)=E[(gk−0)(gj−0)]=0；当 k = j k = j k=j时， Cov ( g k , g j ) = E [ ( g k ) 2 ] \text{Cov}(g_k, g_j) = \mathbb{E}[(g_k)^2] Cov(gk,gj)=E[(gk)2]。

接下来，针对视角k，批量大小为 1 的 Adam 步骤（无动量）对应的参数更新为：
Δ { k } = g k E [ E j ∈ V [ g j 2 ] ] = g k E [ ∣ V ∣ g 2 ∣ V ∣ ] = g k ∣ V ∣ E [ g 2 ] \Delta^{\{k\}} = \frac{g_k}{\sqrt{\mathbb{E}\left[\mathbb{E}_{j \in V}\left[g_j^2\right]\right]}} = \frac{g_k}{\sqrt{\mathbb{E}\left[\frac{|V|g^2}{|V|}\right]}} = \frac{g_k}{\sqrt{|V| \sqrt{\mathbb{E}\left[g^2\right]}}} Δ{k}=E[Ej∈V[gj2]] gk=E[∣V∣∣V∣g2] gk=∣V∣E[g2] gk

然而，对大小为b的视角批量B⊆V执行一次 Adam 步骤（无动量），对应的参数更新为：
Δ { B } = ∑ k ∈ B g k / b E [ E B ′ ⊆ V [ ( ∑ j ∈ B ′ g j ′ / b ) 2 ] ] = ∑ k ∈ B g k / b E [ ∣ V ∣ b g 2 ] = ∑ k ∈ B g k / b ∣ V ∣ b E [ g 2 ] = 1 b ∑ k ∈ B g k ∣ V ∣ E [ g 2 ] \Delta^{\{B\}} = \frac{\sum_{k \in B} g_k / b}{\sqrt{\mathbb{E}\left[\mathbb{E}{B' \subseteq V}\left[\left(\sum{j \in B'} g_j' / b\right)^2\right]\right]}} = \frac{\sum_{k \in B} g_k / b}{\sqrt{\mathbb{E}\left[\frac{|V|}{b}g^2\right]}} = \frac{\sum_{k \in B} g_k / b}{\sqrt{\frac{|V|}{b} \sqrt{\mathbb{E}\left[g^2\right]}}} = \frac{1}{\sqrt{b}} \frac{\sum_{k \in B} g_k}{\sqrt{|V| \sqrt{\mathbb{E}\left[g^2\right]}}} Δ{B}=E[EB′⊆V[(∑j∈B′gj′/b)2]] ∑k∈Bgk/b=E[b∣V∣g2] ∑k∈Bgk/b=b∣V∣E[g2] ∑k∈Bgk/b=b 1∣V∣E[g2] ∑k∈Bgk

因此，将学习率设为 λ ′ = λ × b \lambda' = \lambda \times \sqrt b λ′=λ×b ​，可使批量更新 Δ { B } \Delta^{\{B\}} Δ{B}与各单独更新的总和 ∑ k ∈ B Δ { k } \sum_{k \in B} \Delta^{\{k\}} ∑k∈BΔ{k}相匹配。除了平方根学习率缩放（公式 1），我们还提出了指数动量缩放，以适配更大的批量（公式 2）。该规则最初由 Busbridge 等人（2023）使用，其将动量参数缩放为 β ′ = β batch_size \beta' = \beta^{\text{batch\_size}} β′=βbatch_size------ 当批量大小增大时，这会指数级降低过去梯度的影响。

需要强调的是，实际场景中，尽管部分相机的位姿相似，但随机选取的一组相机会观测场景的不同部分，因此批量内的梯度大多是稀疏的，且可近似视为相互独立。我们通过实验研究了梯度独立假设，并评估了所提出的缩放规则。

5.1 独立梯度的经验证据

为了验证 "梯度独立假设" 在实际场景中是否成立，我们分析了真实环境下梯度在每个参数上的平均方差。我们以 "Rubble" 数据集（Turki 等人，2022）中预训练 checkpoint 里的漫反射颜色参数为例，在图 6 中绘制了其梯度的稀疏性与方差随批量大小变化的曲线。结果显示：方差的倒数先大致呈线性增长，随后趋于平稳。这种规律在代表训练初期、中期、后期的三个 checkpoint 迭代中均存在。

精度（方差的倒数）初期的线性增长表明，在本研究使用的批量大小范围内（最大为 32），梯度大致是不相关的，这为梯度独立假设提供了支持。不过，单张图像的梯度可能是稀疏的；而在大批次中，梯度会出现重叠、稀疏性降低，同时相关性也会增强 ------ 因为位姿相似的相机通常会产生相似的梯度。

5.2 所提出缩放规则的实验验证

为了实证验证所提出的学习率与动量缩放规则，我们先以批量大小 1 训练 "Rubble" 场景至 15000 次迭代。随后重置 Adam 优化器的状态，改用不同批量大小继续训练。在图 12（附录 B.3）中，我们对比了不同学习率与动量缩放规则在切换到更大批量时，对训练轨迹的保持效果。为不失一般性，本次分析聚焦于漫反射颜色参数。

图 12a 对比了三种学习率缩放规则（恒定、平方根、线性），结果显示只有我们提出的 "平方根" 规则能在不同训练批量下，保持较高的更新余弦相似度与相近的更新幅度。类似地，图 12b 表明：我们提出的指数动量缩放规则，相比 "保持动量系数不变" 的方案，能维持更高的更新余弦相似度。