DAY03：【DL 第一弹】神经网络

一、神经网络的概述

1.1 神经网络的定义

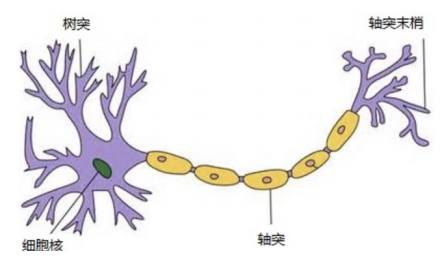
人工神经网络（ANN）是模仿生物大脑神经元结构的计算模型。生物大脑由数十亿神经元组成，每个神经元通过树突接收信号，在细胞体内处理后，通过轴突输出信号到其他神经元。人工神经网络用数学模型模拟这一过程：每个人工神经元接收多个输入信号（类似树突），对信号进行加权求和（模拟细胞体整合信息），再通过激活函数（模拟神经元的兴奋/抑制状态）输出结果。

这种设计使网络能够学习复杂的模式，例如识别图像中的猫或预测股票价格。本质上，神经网络通过调整神经元间的连接权重（即信号传递的强度），逐步逼近真实世界的复杂关系。其核心优势在于分布式并行处理 ：信息在网络中流动时，所有神经元同时参与计算，而非传统计算机的串行处理，这赋予它强大的非线性拟合能力，能解决传统算法难以处理的模式识别、分类等问题。

1.2 神经元的构建

单个神经元的构建是神经网络的基础单元，其工作原理分为三步：

1. 加权求和 ：神经元接收来自前一层多个输入信号x1,x2,...,xnx_1, x_2, \dots, x_nx1,x2,...,xn，每个信号被赋予一个权重w1,w2,...,wnw_1, w_2, \dots, w_nw1,w2,...,wn，表示该信号的重要性。同时加入偏置项bbb作为基础阈值。计算公式为：
   z=w1x1+w2x2+⋯+wnxn+b z = w_1x_1 + w_2x_2 + \dots + w_nx_n + b z=w1x1+w2x2+⋯+wnxn+b
   权重和偏置是网络的核心参数，通过训练不断优化。
2. 激活函数处理 ：将加权求和结果zzz输入激活函数（如Sigmoid、ReLU），引入非线性变换。例如，Sigmoid函数将zzz映射到(0,1)(0,1)(0,1)区间，模拟生物神经元的激活概率；ReLU函数则保留正信号、抑制负信号（f(z)=max⁡(0,z)f(z) = \max(0, z)f(z)=max(0,z)），提升计算效率。
3. 输出结果 ：激活函数的输出作为该神经元的最终信号，传递给下一层神经元。
   

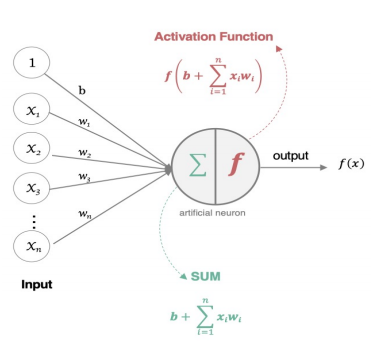
神经元像一个智能投票器，根据输入信号的重要性（权重）和自身偏好（偏置）计算总分，再通过激活函数决定是否发声（输出信号）。这种设计使网络能学习复杂决策边界，而非简单的线性关系。

1.3 神经网络的构建

1.3.1 层级结构

神经网络由多个神经元分层堆叠而成，形成层级结构：

• 输入层：接收原始数据（如图像像素、文本向量），神经元数量等于输入特征数；
• 隐藏层：位于输入层和输出层之间，可包含多层（深度网络）。每层神经元接收前一层所有神经元的输出，进行加权求和和激活函数变换，逐步提取抽象特征。例如，在图像识别中，第一层可能学习边缘特征，第二层组合边缘为纹理，更高层形成物体部件；
• 输出层：给出最终结果（如分类概率、回归值）。

1.3.2 关键特点

1. 全连接：相邻层神经元两两相连，每个连接对应一个权重参数。
2. 信息单向流动 ：数据从输入层 → 隐藏层 → 输出层单向传递，无反向连接（前馈网络）。
3. 层级抽象 ：越深的隐藏层，提取的特征越抽象（如从像素 → 边缘 → 物体部件 → 完整物体）。
   

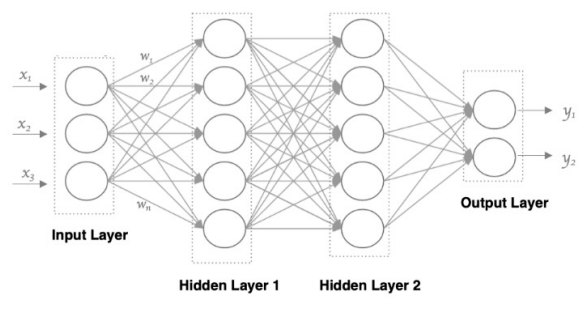
神经网络像一个多层加工厂，输入层是原材料，隐藏层是不同精度的加工车间（粗加工 → 精加工），输出层是成品。全连接设计确保信息充分传递，层级结构使网络能逐步学习从简单到复杂的模式。

1.4 神经网络的组成

1.4.1 输入层

1. 功能：接收外部数据（如用户输入的图片、传感器数据），不做计算，仅传递原始信息。
2. 设计：神经元数量等于输入特征维度。例如，处理28×28像素灰度图时，输入层有784个神经元。

1.4.2 隐藏层

1. 功能：执行核心计算，通过权重和激活函数提取特征。层数和神经元数量决定网络容量（复杂度）。
2. 设计：至少一层，常见为多层（深度网络）。例如，ResNet可有上百层隐藏层。

1.4.3 输出层

1. 功能 ：输出最终结果。根据任务选择激活函数：
   • 分类任务：Softmax（多分类）、Sigmoid（二分类）输出概率；
   • 回归任务：线性激活函数（恒等函数）输出连续值。

输入层是数据入口，隐藏层是特征加工车间，输出层是结果出口。数据仅从输入层 → 隐藏层 → 输出层单向流动，无层内或跨层连接（前馈网络）。这种结构简化了训练过程，使梯度反向传播算法（BP算法）能有效优化参数，同时确保信息处理有序，避免循环依赖。

1.5 神经网络的特点

神经网络具有五大核心特点，奠定其独特优势：

1. 层内无连接：同一层神经元互不连接，仅接收前一层输出。这简化了计算复杂度，避免层内信号干扰。
2. 全连接（Full Connected） ：相邻层神经元两两相连。例如，第NNN层有mmm个神经元，第N−1N-1N−1层有nnn个神经元，则连接数为m×nm \times nm×n。全连接确保信息充分传递，但参数量随层数指数增长（易导致过拟合）。
3. 单向信息流：数据从输入层 → 隐藏层 → 输出层单向传递，无反馈回路。这使训练过程可解（通过BP算法），但限制了处理时序数据的能力（需RNN/LSTM等变体）。
4. 权重参数化 ：每个连接对应权重www和偏置bbb，是网络的可学习参数。训练过程本质是优化这些参数，使输出逼近真实标签。

神经网络像层级投票系统：每层神经元独立投票（层内无连接），但投票依据来自上一层所有神经元（全连接），投票结果逐层传递（单向流），最终通过调整投票权重（参数）提升决策准确性。

1.6 神经网络的优点

神经网络在众多领域超越传统方法，核心优势如下：

1. 高精度与强性能：在图像识别（如ImageNet竞赛）、语音识别（如语音助手）、自然语言处理（如机器翻译）等任务中，准确率常超过人类水平。
2. 非线性拟合能力：通过激活函数（如ReLU、Sigmoid）引入非线性，结合多层结构，神经网络能逼近任意复杂函数（万能逼近定理）。这使其能处理高维非线性问题（如医疗诊断、金融预测）。
3. 生态完善与硬件加速：主流框架（PyTorch、TensorFlow）提供便捷API，支持自动求导、GPU加速。硬件发展（如NVIDIA GPU、TPU）大幅缩短训练时间，使大规模网络（如GPT-3）成为可能。

神经网络像超级学徒，能从海量数据中学习复杂规律（高精度），理解弯弯绕绕的关系（非线性拟合），且有高级工具（框架+硬件）辅助，快速成长为专家。

1.7 神经网络的缺点

尽管强大，神经网络存在显著局限性：

1. 黑箱特性：难以解释决策依据。例如，图像分类模型可能因背景而非物体本身做出判断，但无法说明原因。这在医疗、金融等高风险领域引发信任危机。
2. 训练成本高昂：大型网络（如GPT-3）需数周训练，消耗大量计算资源（数千GPU小时）和电力（相当于数百家庭年用电量）。
3. 超参数调优复杂：需手动设计层数、神经元数、学习率等超参数，依赖经验和试错。例如，层数过浅导致欠拟合，过深引发梯度消失。
4. 数据依赖与过拟合：小数据集上表现差（易过拟合），需大量标注数据。例如，医疗影像诊断需数千张标注图像，而传统方法可能仅需百张。

神经网络像神秘天才，能力超强但说不出思路（黑箱），培养成本极高（训练耗资源），成长需定制化方案（调参），且挑食------没足够数据就学不好（数据依赖）。

二、激活函数

2.1 激活函数的作用

2.1.1 引入非线性因素，突破线性模型的局限

在神经网络中，若没有激活函数，无论网络结构多深，其本质仍是一个线性模型 。这是因为线性变换的叠加仍是线性的：
y=W2(W1x+b1)+b2=(W2W1)x+(W2b1+b2) y = W_2(W_1x + b_1) + b_2 = (W_2W_1)x + (W_2b_1 + b_2) y=W2(W1x+b1)+b2=(W2W1)x+(W2b1+b2)

这种模型只能学习直线关系 ，无法拟合现实世界中普遍存在的非线性规律（如曲线、周期性波动等）。激活函数的核心价值在于为网络注入非线性能力。它像一个智能开关，对每个神经元的输出进行非线性变换，使网络能够组合出复杂的决策边界。

• Sigmoid函数将输出压缩到(0,1)，模拟概率分布；
• ReLU函数保留正信号、屏蔽负信号，形成分段线性结构；
• Tanh函数输出在(-1,1)之间，适合对称性数据。

线性模型如同只能画直线的尺子，而激活函数赋予网络万能画笔。比如，用直线无法拟合圆形或波浪形数据，但加入激活函数后，网络能通过多段曲线拼接逼近任意形状------这正是深度学习解决图像识别、自然语言处理等复杂问题的基石。

2.1.2 提升网络表达能力，逼近任意复杂函数

激活函数使神经网络具备了万能近似定理（Universal Approximation Theorem） 的理论基础：只要网络足够宽或足够深，且使用非线性激活函数，它就能以任意精度逼近任何连续函数。这意味着：

1. 解决复杂问题 ：
   • 图像识别中，激活函数帮助网络识别边缘、纹理、物体部件等层级特征；
   • 自然语言处理中，它能捕捉语义的上下文依赖关系（如"苹果"在"吃苹果"和"苹果手机"中的不同含义）。
2. 特征自动学习 ：隐藏层的激活函数将输入数据逐步抽象为高级特征。例如：
   • 第一层激活函数检测像素边缘；
   • 第二层组合边缘为轮廓；
   • 第三层组合轮廓为物体部件。

激活函数如同翻译官，将原始数据（如像素点）翻译成有意义的特征（如猫耳朵、狗鼻子）。没有它，网络只能机械地做加权求和，就像只会背单词却不懂语法的人，无法理解句子含义。激活函数让网络学会思考，从数据中挖掘深层规律。

2.1.3 控制信号流动，优化梯度传播

激活函数的数学特性直接影响梯度反向传播的效率：

1. 梯度消失问题 ：Sigmoid/Tanh函数在输入绝对值较大时（如∣x∣>6|x|>6∣x∣>6），导数趋近于0。这使得深层网络中梯度逐层衰减，底层参数几乎不更新，导致模型停滞。
2. 梯度爆炸问题 ：若激活函数导数>1>1>1（如未归一化的线性函数），梯度在反向传播中逐层放大，导致参数震荡发散。
3. 现代激活函数的改进 ：
   • ReLU：在正区间导数恒为1，缓解梯度消失；
   • Leaky ReLU：负区间保留微小斜率（如0.01），避免神经元死亡；
   • Swish：结合平滑性与非单调性，提升深层网络表现。

激活函数如同信号调节器。Sigmoid像老旧水管，水流（梯度）经过时严重衰减；ReLU像智能阀门，正向水流畅通无阻，负向水流直接截断。选择合适的激活函数，就是为神经网络铺设高效的信息高速公路，确保梯度信号能从输出层顺利传递到输入层，驱动参数优化。

2.2 常见的激活函数

2.2.1 Sigmoid函数

Sigmoid函数作为深度学习的开山鼻祖，其核心价值在于将线性输入转化为非线性概率输出 ，为神经网络解决复杂问题奠定基础。然而，其梯度消失 、非零中心 、计算昂贵等缺陷，使其在隐藏层中被ReLU等函数取代，如今仅作为二分类输出层的专用工具。理解Sigmoid的优缺点，是掌握现代激活函数（如ReLU、Swish）的关键基石。

（1）数学表示

• sigmoid函数的数学公式：
  f(x)=11+e−x f(x) = \frac{1}{1 + e^{-x}} f(x)=1+e−x1

• sigmoid函数的导数公式：
  f′(x)=(11+e−x)′=11+e−x(1−11+e−x)=f(x)(1−f(x)) f'(x) = \left( \frac{1}{1 + e^{-x}} \right)' = \frac{1}{1 + e^{-x}} \left( 1 - \frac{1}{1 + e^{-x}} \right) = f(x)(1 - f(x)) f′(x)=(1+e−x1)′=1+e−x1(1−1+e−x1)=f(x)(1−f(x))

（2）可视化表示

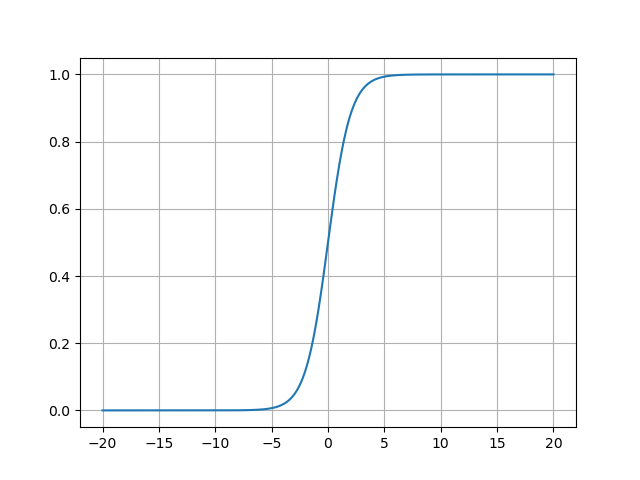
• Sigmoid函数的图像：
  

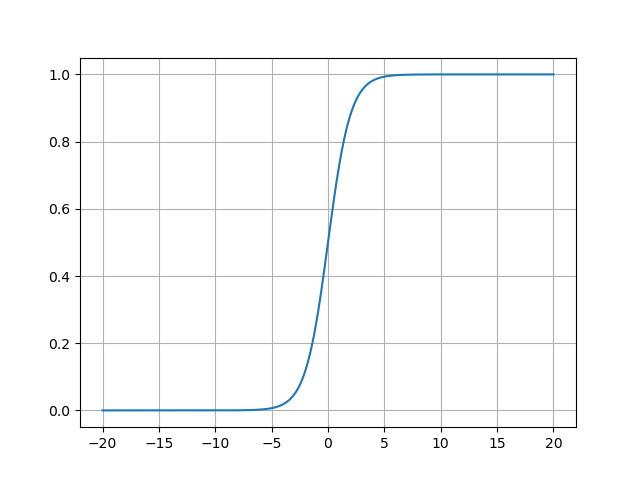
Sigmoid函数的图像呈现平滑的S形曲线，其关键特征如下：

• 敏感区间 ：输入值在[−3,3][-3, 3][−3,3]时，输出从0.05陡增至0.95，此区间内函数对输入变化高度敏感；
• 饱和区间 ：当x<−6x < -6x<−6或x>6x > 6x>6时，输出分别趋近于0和1，曲线进入平台期，输入的微小变化几乎不影响输出；
• 对称性 ：函数关于点(0,0.5)(0, 0.5)(0,0.5)中心对称，但输出不以0为中心（均值约为0.5）。

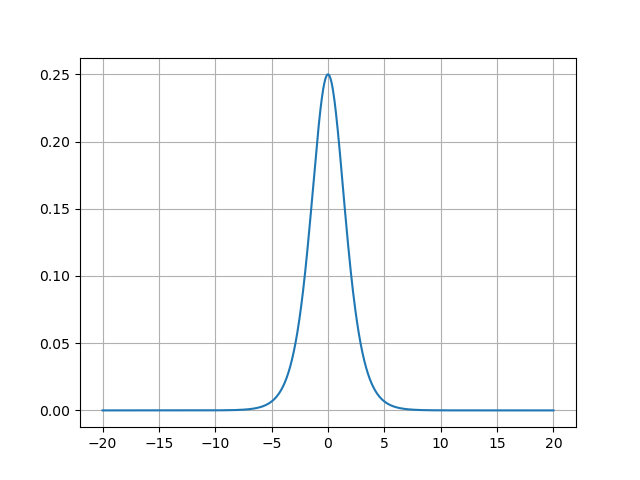
• Sigmoid函数的导数图像：
  

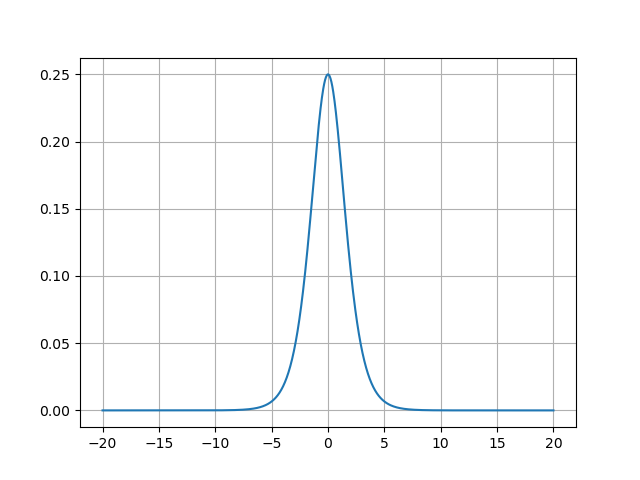
Sigmoid函数的导数图像呈钟形分布，其关键特征如下：

• 峰值在x=0x=0x=0处，导数最大为0.25；
• 当∣x∣>3|x| > 3∣x∣>3时，导数迅速衰减至接近0；
• 当∣x∣>6|x| > 6∣x∣>6时，导数几乎为0，形成梯度消失区。

（3）功能

Sigmoid函数的核心功能是引入非线性变换，使神经网络能够拟合复杂模式：

1. 概率映射 ：将任意实数输入压缩到(0,1)(0, 1)(0,1)，输出值可视为概率（如二分类中正类的置信度）。
2. 非线性激活：若网络中无激活函数，多层线性层等价于单层线性模型，无法解决非线性问题（如XOR问题）。Sigmoid函数通过非线性变换，赋予网络拟合任意复杂函数的能力。
3. 输出层适配：在二分类任务中，Sigmoid函数的输出天然符合概率分布，可直接与交叉熵损失函数配合使用。

（4）特点

Sigmoid函数的特点决定了其在现代深度学习中的局限性：

1. 梯度消失问题 ：
   • 当输入绝对值较大∣x∣>6|x|>6∣x∣>6时，导数趋近于0，参数更新几乎停止；
   • 在5层以上的网络中，梯度逐层累积衰减，浅层参数无法有效学习。
2. 非零中心输出 ：
   • 输出恒为正（均值≈0.5），导致反向传播时梯度方向单一（如w⋅gradw \cdot \text{grad}w⋅grad始终为正），参数更新效率低下；
   • 对比Tanh（输出均值为0），Sigmoid的收敛速度更慢。
3. 计算成本高 ：
   • 包含指数运算e−xe^{-x}e−x，计算量远大于ReLU等分段线性函数；
   • 在GPU并行计算中，指数运算成为性能瓶颈。
4. 适用场景受限 ：
   • 仅适合二分类输出层，隐藏层已被ReLU等函数取代；
   • 在多分类任务中，需配合Softmax使用。

（5）代码示例

import torch
import matplotlib.pyplot as plt

# 原函数
x = torch.linspace(-20, 20, 1000)
y = torch.sigmoid(x)
plt.plot(x.numpy(), y.numpy())
plt.grid()
plt.show()

# 导函数
x_ = torch.linspace(-20, 20, 1000, requires_grad=True)
torch.sigmoid(x_).sum().backward()
plt.plot(x_.detach().numpy(), x_.grad.numpy())
plt.grid()
plt.show()

• 代码输出：
  
  

2.3.2 Tanh函数

（1）数学表示

• Tanh函数的数学公式：
  f(x)=1−e−2x1+e−2x f(x) = \frac{1 - e^{-2x}}{1 + e^{-2x}} f(x)=1+e−2x1−e−2x

• Tanh函数的导数公式：
  f′(x)=(1−e−2x1+e−2x)′=1−f2(x) f'(x) = \left( \frac{1 - e^{-2x}}{1 + e^{-2x}} \right)' = 1 - f^2(x) f′(x)=(1+e−2x1−e−2x)′=1−f2(x)

（2）可视化表示

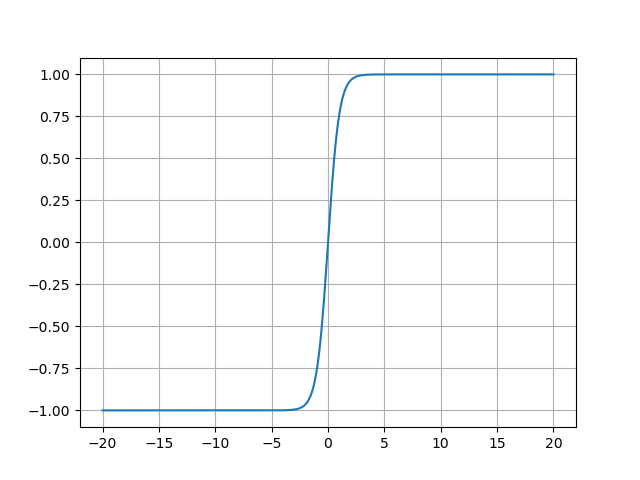
• Tanh函数的图像：
  

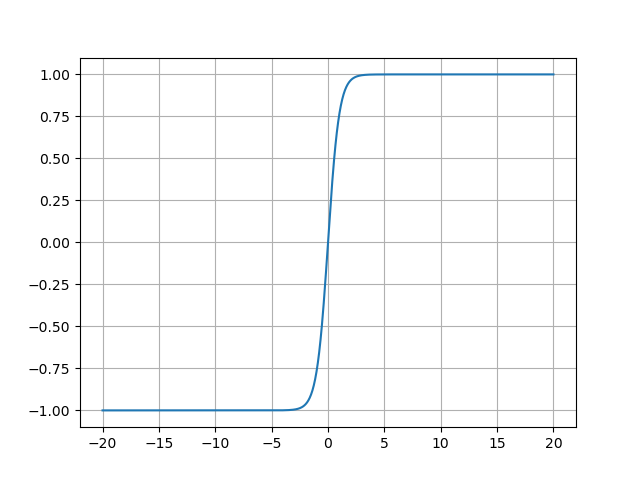
Tanh函数的图像呈现典型的S形曲线，其关键特征包括：

• 中心对称性 ：曲线关于原点(0,0)(0,0)(0,0)对称，过原点且斜率最大（导数为1）；
• 饱和区 ：当x<−3x < -3x<−3时，输出趋近于-1；当x>3x > 3x>3时，输出趋近于1；
• 线性区 ：在[−1,1][-1, 1][−1,1]区间内，函数近似线性，对微小输入变化敏感。

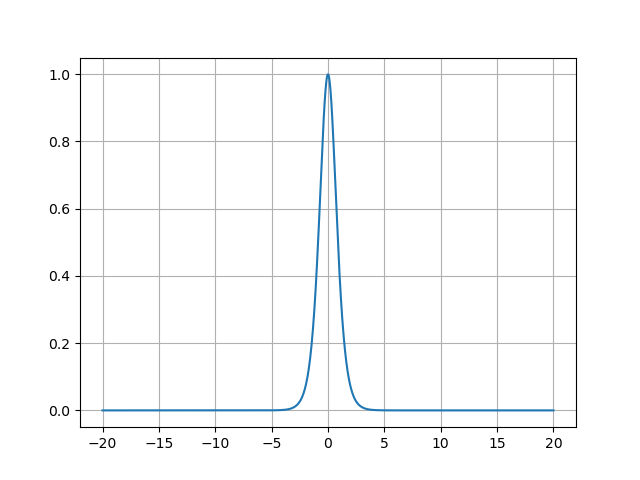
• Tanh函数的导数图像：
  

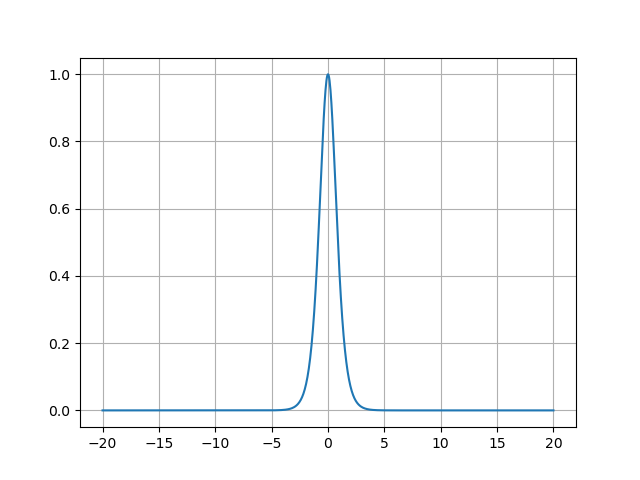
Tanh函数的导数图像呈钟形，其关键特征如下：

• 峰值在原点 ：x=0x=0x=0时导数达到最大值1，表明此处梯度传递效率最高；
• 两侧衰减 ：当∣x∣>3|x| > 3∣x∣>3时，导数趋近于0，导致梯度消失；
• 梯度传播影响 ：在[−2,2][-2, 2][−2,2]区间内导数大于0.1，而Sigmoid仅在[−1.5,1.5][-1.5, 1.5][−1.5,1.5]内满足此条件。这意味着Tanh在更宽的输入范围内能有效传递梯度，缓解深层网络的梯度消失问题；
• 饱和区风险 ：当输入绝对值过大时（如∣x∣>5|x| > 5∣x∣>5），导数接近0，权重更新几乎停滞。例如，若某层神经元输出全为±1\pm 1±1，则梯度无法反向传播，该层成为死区。

（3）功能

Tanh函数的核心功能是将输入值映射到(−1,1)(-1, 1)(−1,1)区间，同时引入非线性变换，具体作用如下：

1. 零中心化输出：输出均值为0，符合自然数据分布（如去均值后的图像像素）。这种特性使下一层神经元的输入更均衡，避免梯度更新方向偏移。例如，在RNN中，Tanh的零中心输出可防止长期依赖中的梯度累积偏置。
2. 非线性增强：通过S形曲线将线性输入转化为非线性输出，使网络能拟合复杂模式。例如，在语音识别中，Tanh能将声波信号的线性特征转化为音素间的非线性关联。
3. 梯度优化 ：相比Sigmoid，Tanh的导数范围(0,1)(0, 1)(0,1)更大（Sigmoid为(0,0.25)(0, 0.25)(0,0.25)），在相同输入下梯度强度更高。例如，当x=0x=0x=0时，Tanh导数为1，而Sigmoid仅为0.25，这使Tanh在反向传播中能传递更强的梯度信号。

（4）与Sigmoid函数的区别

Tanh与Sigmoid虽同属S型激活函数，但在设计哲学和实际表现上存在显著差异：

特性	Tanh函数	Sigmoid函数
输出范围	(−1,1)(-1, 1)(−1,1)	(0,1)(0, 1)(0,1)
中心对称性	零中心（均值为0）	正偏置（均值为0.5）
导数最大值	1（在x=0x=0x=0处）	0.25（在x=0x=0x=0处）
梯度强度	更强（导数衰减慢）	较弱（导数衰减快）
适用场景	隐藏层、RNN门控	二分类输出层

1. 梯度效率对比 ：在反向传播中，梯度需逐层相乘。假设某层输入为x=1x=1x=1：
   • Tanh导数：f′(1)≈0.42f'(1) \approx 0.42f′(1)≈0.42
   • Sigmoid导数：f′(1)≈0.2f'(1) \approx 0.2f′(1)≈0.2

经过5层传播后，Tanh的梯度保留0.425≈0.0130.42^5 \approx 0.0130.425≈0.013，而Sigmoid仅剩0.25=0.000320.2^5 = 0.000320.25=0.00032，相差40倍，这就解释了为何Tanh在深层网络中收敛更快。

2. 偏置问题 ：
   Sigmoid的输出恒为正，导致下一层神经元的输入同号（如w1x1+w2x2w_1x_1 + w_2x_2w1x1+w2x2中x1,x2>0x_1, x_2 > 0x1,x2>0）。这种正相关偏置使优化路径曲折（如Z字型下降），而Tanh的零中心输出使权重更新方向更直接。

（5）适用场景

Tanh特别适合需要对称输出的任务，如LSTM中的门控机制（遗忘门/输入门需平衡正负信号），或生成对抗网络（GAN）中生成器的输出层（需对称噪声分布）。

（6）代码示例

import torch
import matplotlib.pyplot as plt

# 原函数
x = torch.linspace(-20, 20, 1000)
y = torch.tanh(x)
plt.plot(x.numpy(), y.numpy())
plt.grid()
plt.show()

# 导函数
x_ = torch.linspace(-20, 20, 1000, requires_grad=True)
torch.tanh(x_).sum().backward()
plt.plot(x_.detach().numpy(), x_.grad.numpy())
plt.grid()
plt.show()

• 代码输出：
  
  

2.3.3 ReLU函数

（1）数学表示

• ReLU函数的数学公式：
  f(x)=max⁡(0,x) f(x) = \max(0, x) f(x)=max(0,x)

• ReLU函数的的导数公式：
  f′(x)={0if x<01if x≥0 f'(x) = \begin{cases} 0 & \text{if } x < 0 \\ 1 & \text{if } x \geq 0 \end{cases} f′(x)={01if x<0if x≥0

（2）可视化表示

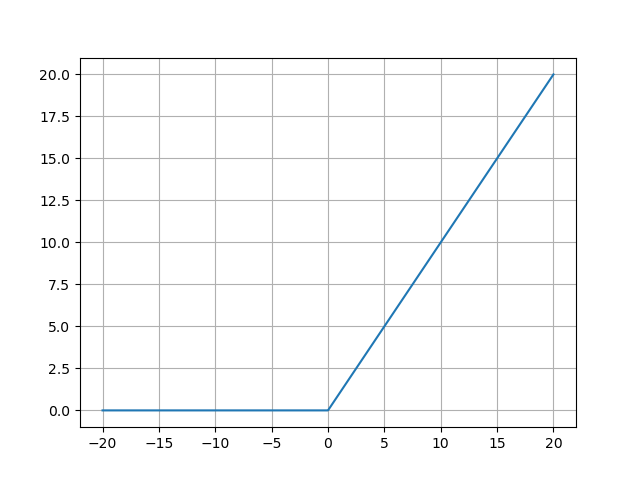
• ReLU函数的图像：
  
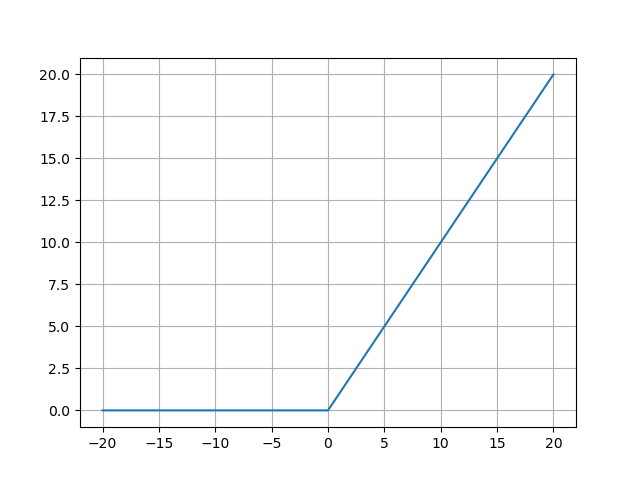
  ReLU函数的图像呈现为L型折线：
  • 左侧x<0x < 0x<0：水平线y=0y=0y=0，表示所有负输入被压缩为零；
  • 右侧x≥0x \geq 0x≥0：斜率为1的直线y=xy=xy=x，保留原始输入值。

这种非对称设计使ReLU的输出非负 （范围[0,+∞)[0, +\infty)[0,+∞)），符合生物神经元激活或静默的特性。

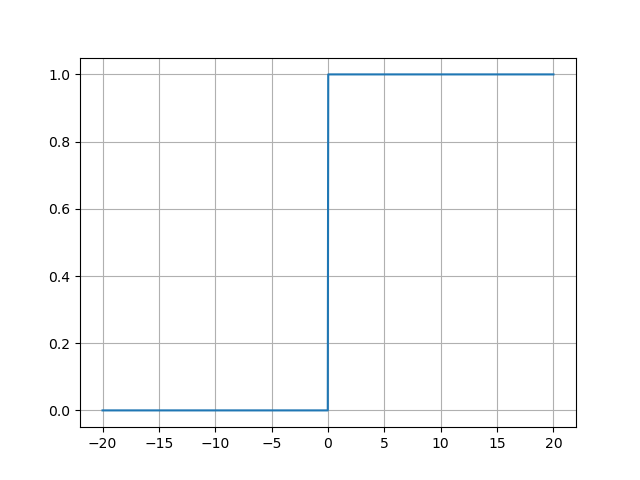
• ReLU函数的导数图像：
  
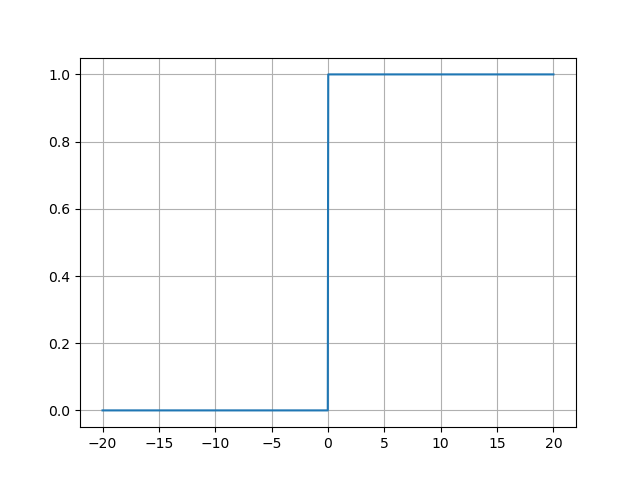
  ReLU函数的导数图像呈现为阶梯状分布：
  • 负区间：导数恒为0（梯度消失），对应函数图像的平坦区域；
  • 正区间：导数恒为1（梯度无损传递），对应函数图像的斜线区域。

在x=0x=0x=0处导数不连续，但实际应用中通常定义为0或1，不影响训练效果。

（3）功能

ReLU的核心功能是引入非线性并加速收敛：

1. 非线性变换：通过分段线性操作，使网络能够拟合复杂曲线。若没有ReLU，多层线性网络等价于单层线性模型，无法解决非线性问题（如XOR分类）。
2. 稀疏激活 ：约50%的神经元输出为零（负输入被抑制），形成稀疏表示。这减少了参数间的耦合，提升模型泛化能力，类似大脑中神经元的选择性激活。
3. 计算高效 ：仅涉及比较和取最大值操作，计算复杂度为O(1)O(1)O(1)，远低于Sigmoid的指数运算O(ex)O(e^x)O(ex)。

（4）特点

ReLU的优缺点鲜明，需结合场景权衡：

• 优点 ：
  1. 缓解梯度消失：在正区间梯度恒为1，使深层网络（如CNN、Transformer）能有效训练。
  2. 收敛速度快：线性特性使优化路径更平滑，实验表明其收敛速度比Sigmoid快6倍。
  3. • 生物学合理性：模拟大脑神经元的"兴奋-抑制"机制（负输入对应静默状态）。
• 缺点 ：
  1. 神经元死亡（Dying ReLU）：若输入长期为负（如学习率过大导致权重偏移），神经元输出恒为零且梯度无法更新，永久失效。
  2. 输出非零中心化：均值偏向正值（如输入服从标准正态分布时，ReLU输出均值约0.5），可能导致后续层权重更新偏移。

（5）与Sigmoid函数的区别

ReLU与Sigmoid的对比是深度学习演进的关键：

特性	ReLU	Sigmoid
输出范围	[0,+∞)[0, +\infty)[0,+∞)	(0,1)(0, 1)(0,1)
梯度行为	正区间梯度=1（无衰减）	最大梯度=0.25（易消失）
计算效率	仅需比较操作（极快）	需指数运算（较慢）
稀疏性	50%神经元输出为0（天然稀疏）	所有神经元激活（密集表示）
适用场景	隐藏层（尤其CNN/RNN）	二分类输出层

1. 梯度传递 ：Sigmoid的导数最大仅0.25，反向传播时梯度逐层缩放（如5层网络后梯度衰减至0.255≈0.0010.25^5 \approx 0.0010.255≈0.001），而ReLU在正区间梯度恒为1，可无损传递。
2. 计算开销 ：Sigmoid的e−xe^{-x}e−x运算在GPU上耗时显著，ReLU的max⁡(0,x)\max(0,x)max(0,x)则近乎零成本。
3. 表示能力：Sigmoid的密集激活易导致特征冗余，ReLU的稀疏性更接近生物系统，且能自动筛选重要特征。

（6）代码示例

import torch
import matplotlib.pyplot as plt

# 原函数
x = torch.linspace(-20, 20, 1000)
y = torch.relu(x)
plt.plot(x.numpy(), y.numpy())
plt.grid()
plt.show()

# 导函数
x_ = torch.linspace(-20, 20, 1000, requires_grad=True)
torch.relu(x_).sum().backward()
plt.plot(x_.detach().numpy(), x_.grad.numpy())
plt.grid()
plt.show()

• 代码输出：
  
  

2.3.4 Softmax函数

（1）数学表示

• Softmax函数的数学公式：
  softmax(zi)=ezi∑jezj \text{softmax}(z_i) = \frac{e^{z_i}}{\sum_j e^{z_j}} softmax(zi)=∑jezjezi

（2）功能

Softmax函数是多分类任务的标准输出层激活函数 ，其核心功能是将神经网络的原始输出（称为Logits）转换为概率分布，为模型提供可解释的预测结果：

1. 概率转换 ：神经网络最后一层的输出（Logits）是未归一化的实数，可能为负值或超出[0,1][0, 1][0,1]范围。Softmax将其转换为概率值，例如输入[1.0,2.0,3.0][1.0, 2.0, 3.0][1.0,2.0,3.0]转换为[0.09,0.24,0.67][0.09, 0.24, 0.67][0.09,0.24,0.67]，可直接解释为"类别0概率9%，类别1概率24%，类别2概率67%"。
2. 决策依据：在多分类问题中（如手写数字识别0~9），模型需选择概率最高的类别作为预测结果。Softmax的赢家通吃特性（指数放大最大值）使最大概率值显著高于其他值，便于模型做出明确决策。
3. 损失函数兼容性 ：Softmax的输出与交叉熵损失函数（Cross-Entropy Loss）天然适配。交叉熵衡量真实概率分布（如标签[0,1,0][0, 1, 0][0,1,0]）与预测概率分布的差异，而Softmax的输出正是预测概率分布，二者结合可高效优化模型参数。

（3）特点

• 优势：
  1. 非负性 ：指数函数ezi>0e^{z_i} > 0ezi>0，确保输出概率恒为正。
  2. 归一性：分母的求和操作强制输出概率之和为1。
  3. 单调性 ：若zi>zjz_i > z_jzi>zj，则softmax(zi)>softmax(zj)\text{softmax}(z_i) > \text{softmax}(z_j)softmax(zi)>softmax(zj)，保留原始输入的大小关系。
• 局限：
  1. 数值稳定性 ：当输入值过大时，ezie^{z_i}ezi可能溢出。实际应用中常采用Log-Sum-Exp技巧（减去最大值）提升稳定性。
  2. 类别不平衡：若某类别样本极少，Softmax可能低估其概率，此时需结合代价敏感学习或类别权重调整。

（4）代码示例

import torch

scores = torch.tensor([0.2, 0.02, 0.15, 0.15, 1.3, 0.5, 0.06, 1.1, 0.05, 3.75])
print(f"scores：{scores}")

probabilities = torch.softmax(scores, dim=0)
print(f"probabilities：{probabilities}")

• 代码输出：

  scores：tensor([0.2000, 0.0200, 0.1500, 0.1500, 1.3000, 0.5000, 0.0600, 1.1000, 0.0500,
  3.7500])
  probabilities：tensor([0.0212, 0.0177, 0.0202, 0.0202, 0.0638, 0.0287, 0.0185, 0.0522, 0.0183,
  0.7392])

2.4 其他的激活函数

函数	数学公式	导数公式	取值范围	功能	函数签名	参数说明
Identity Function（恒等函数）	f(x)=xf(x) = xf(x)=x	f′(x)=1f'(x) = 1f′(x)=1	(−∞,+∞)(-\infty, +\infty)(−∞,+∞)	保持输入不变，无非线性变换，常用于需要线性传递的场景（如残差连接、回归任务输出层）。	torch.nn.Identity(inplace=False)	- inplace：布尔值，默认False。若为True，会原地修改输入张量（直接覆盖原数据）；若为False，返回输入张量的副本（不改变原数据）。
Leaky ReLU（泄漏整流线性单元）	f(x)={αxx<0xx≥0f(x) = \begin{cases} \alpha x & x < 0 \\ x & x \geq 0 \end{cases}f(x)={αxxx<0x≥0	f′(x)={αx<01x≥0f'(x) = \begin{cases} \alpha & x < 0 \\ 1 & x \geq 0 \end{cases}f′(x)={α1x<0x≥0	(−∞,+∞)(-\infty, +\infty)(−∞,+∞)	解决ReLU的dying ReLU 问题（负输入时梯度为0导致神经元死亡），负区间保留非零斜率α\alphaα，使梯度持续流动。	torch.nn.LeakyReLU(negative_slope=0.01, inplace=False)	- negative_slope：负区间的斜率α\alphaα，默认0.01； - inplace：同Identity的inplace参数。
Parametric ReLU（PReLU，参数化ReLU）	f(α,x)={αxx<0xx≥0f(\alpha, x) = \begin{cases} \alpha x & x < 0 \\ x & x \geq 0 \end{cases}f(α,x)={αxxx<0x≥0	f′(α,x)={αx<01x≥0f'(\alpha, x) = \begin{cases} \alpha & x < 0 \\ 1 & x \geq 0 \end{cases}f′(α,x)={α1x<0x≥0	(−∞,+∞)(-\infty, +\infty)(−∞,+∞)	让负区间的斜率α\alphaα成为可学习的参数，而非固定值，能自适应不同任务的数据分布，比Leaky ReLU更灵活。	torch.nn.PReLU(num_parameters=1, init=0.25, device=None)	- num_parameters：共享参数的数量（1表示单参数，多通道共享；更多则每个通道独立）； - init：初始α\alphaα值，默认0.25； - device：指定参数所在的设备（CPU/GPU）。
Randomized Leaky ReLU（RReLU，随机泄漏ReLU）	f(α,x)={αxx<0xx≥0f(\alpha, x) = \begin{cases} \alpha x & x < 0 \\ x & x \geq 0 \end{cases}f(α,x)={αxxx<0x≥0（α\alphaα从均匀分布[lower,upper][\text{lower}, \text{upper}][lower,upper]采样）	f′(α,x)={αx<01x≥0f'(\alpha, x) = \begin{cases} \alpha & x < 0 \\ 1 & x \geq 0 \end{cases}f′(α,x)={α1x<0x≥0	(−∞,+∞)(-\infty, +\infty)(−∞,+∞)	训练时α\alphaα从均匀分布随机采样，测试时用训练阶段α\alphaα的平均值，增强模型的鲁棒性和泛化能力。	torch.nn.RReLU(lower=1/8, upper=1/3, inplace=False)	- lower：α\alphaα的随机下限，默认1/8； - upper：α\alphaα的随机上限，默认1/3（训练时从均匀分布采样，测试时用两者平均值）； - inplace：同Identity的inplace参数。
Exponential Linear Unit（ELU，指数线性单元）	f(α,x)={α(ex−1)x<0xx≥0f(\alpha, x) = \begin{cases} \alpha (e^x - 1) & x < 0 \\ x & x \geq 0 \end{cases}f(α,x)={α(ex−1)xx<0x≥0	f′(α,x)={f(α,x)+αx<01x≥0f'(\alpha, x) = \begin{cases} f(\alpha, x) + \alpha & x < 0 \\ 1 & x \geq 0 \end{cases}f′(α,x)={f(α,x)+α1x<0x≥0	(−α,+∞)(-\alpha, +\infty)(−α,+∞)	负区间采用指数函数，输出均值接近0，缓解梯度消失问题，加速模型收敛；同时平滑过渡（包括x=0处），提升训练稳定性。	torch.nn.ELU(alpha=1.0, inplace=False)	- alpha：负区间的缩放因子，默认1.0； - inplace：同Identity的inplace参数。

2.5 激活函数的选择

2.5.1 对于隐藏层

隐藏层的主要任务是提取特征并引入非线性，使网络能够拟合复杂模式。选择激活函数需平衡计算效率、梯度传递和稀疏性：

1. 优先选择ReLU（Rectified Linear Unit）
   • 适用场景：绝大多数隐藏层场景（如图像识别、自然语言处理），尤其适合深层网络。例如，ResNet、BERT等主流架构均默认使用ReLU。
   • 解决方式：
     1. 计算高效 ：仅需比较运算max(0, x)，无复杂指数或除法，适合大规模深度网络（如CNN、Transformer）。
     2. 缓解梯度消失：当输入为正时，梯度恒为1，确保深层网络中梯度稳定传递，避免像Sigmoid/Tanh在饱和区梯度趋近于0的问题。
     3. 稀疏激活：负输入直接输出0，使部分神经元休眠，减少参数耦合，提升模型鲁棒性（类似生物神经元的选择性响应）。
2. 若ReLU效果不佳，尝试变体Leaky ReLU 、PReLU
   • 适用场景：ReLU存在神经元死亡问题------若输入持续为负（如初始化不当或学习率过高），该神经元梯度永久为0，导致参数无法更新。
   • 解决方式：
     • Leaky ReLU：负区间保留微小斜率（如f(x)=0.01x），确保梯度持续流动；
     • PReLU（Parametric ReLU）：将负斜率设为可学习参数，让网络自适应调整（如f(x)=αx，α通过训练优化）。
3. 避免使用Sigmoid ，谨慎使用Tanh
   • 适用场景：仅在特定任务（如RNN门控机制）或浅层网络中使用，隐藏层应优先选择ReLU及其变体。
   • 对于Sigmoid：
     • 输出非零中心化（均值≈0.5），导致梯度更新方向震荡（如Z字形优化路径）；
     • 梯度最大值仅0.25，深层网络中梯度逐层衰减，5层以上即出现梯度消失。
   • 对于Tanh：
     • 输出以0为中心（范围[−1,1][-1,1][−1,1]），梯度更新更稳定；
     • 两侧饱和区梯度仍趋近于0，深层网络中仍可能梯度消失。

2.5.2 对于输出层

输出层的核心任务是将网络输出转换为任务目标格式（如概率、连续值），需严格匹配问题类型：

1. 二分类问题 → Sigmoid函数
   • 功能：将任意实数映射到(0,1)(0,1)(0,1)区间，输出单一概率值（如"是否为猫"的概率）。
   • 与损失函数的协同：交叉熵损失L=−[ylog(p)+(1−y)log(1−p)]L = -[y log(p) + (1-y) log(1-p)]L=−[ylog(p)+(1−y)log(1−p)]，与Sigmoid结合后梯度为p−yp-yp−y，避免梯度消失（如MSE在Sigmoid饱和区梯度极小）。当预测错误时（如y=1y=1y=1但p≈0p≈0p≈0），梯度接近1，驱动参数快速修正。
   • 典型场景：医学诊断（患病/健康）、垃圾邮件检测（垃圾/正常）等二元决策任务。
2. 多分类问题 → Softmax函数
   • 功能：将K个类别的原始输出（logits）转换为概率分布：P(y=i∣x)=ezi∑j=1KezjP(y=i|x) = \frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}}P(y=i∣x)=∑j=1Kezjezi。所有类别概率和为1，且通过指数运算放大最大值（如ziz_izi最大时P(y=i∣x)P(y=i|x)P(y=i∣x)显著领先）。
   • 与交叉熵的协同：损失函数L=−∑yilog(pi)L = -∑ y_i log(p_i)L=−∑yilog(pi)，梯度为pi−yip_i - y_ipi−yi：
     • 若预测正确（yi=1y_i=1yi=1且pi≈1p_i≈1pi≈1），梯度接近0；
     • 若预测错误（yi=1y_i=1yi=1但pi≈0p_i≈0pi≈0），梯度接近1，推动模型修正。
   • 典型场景：图像分类（ImageNet的1000类）、文本情感分析（积极/中性/消极）等互斥类别任务。
3. 回归问题 → 恒等函数（Identity Function）
   • 功能：直接输出原始值f(x)=xf(x)=xf(x)=x，不进行非线性变换。回归任务需预测连续值（如房价、温度），激活函数会扭曲数值尺度（如Sigmoid将输出限制在(0,1)(0,1)(0,1)）。
   • 与损失函数的选择
     • MSE（均方误差） ：L=(ypred−ytrue)2L = (y_pred - y_true)^2L=(ypred−ytrue)2，对异常值敏感；
     • MAE（平均绝对误差） ：L=∣ypred−ytrue∣L = |y_pred - y_true|L=∣ypred−ytrue∣，鲁棒性更强；
     • Smooth L1 ：结合MSE和MAE优势，在∣x∣<1|x|<1∣x∣<1时用MSE保证平滑性，∣x∣≥1|x|≥1∣x∣≥1时用MAE避免梯度爆炸。
   • 典型场景：股票预测、销量预测、物理量回归等连续值输出任务。

2.5.3 整体选择逻辑

场景	首选激活函数	备选方案	核心原则
隐藏层	ReLU	Leaky ReLU / PReLU	"效率 + 梯度 + 稀疏性"三位一体
二分类输出	Sigmoid	---	概率输出与交叉熵的天然契合
多分类输出	Softmax	---	互斥类别的概率分布强制约束
回归输出	恒等函数	---	保持数值尺度，避免非线性扭曲

隐藏层活用ReLU，慎用饱和函数 ；输出层任务定函数，概率归一化。正确选择激活函数，是模型从能运行到高性能的关键一步。

三、参数初始化

3.1 常见方法

3.1.1 均匀分布初始化

（1）函数定义

torch.nn.init.uniform_(tensor, a=0.0, b=1.0)  

• 功能：在指定区间内随机生成权重值，确保模型训练初期不会因权重过大或过小导致梯度消失或爆炸。
• 参数说明 ：
  • tensor ：待初始化的权重张量，通常为nn.Linear层的weight属性。例如，linear1.weight是一个形状为(out_features, in_features)的二维张量；
  • a：均匀分布的下界，默认为0.0。在神经网络中常设为负值（如−1/√d-1/√d−1/√d）以生成对称区间；
  • b：均匀分布的上界，默认为1.0。在神经网络中常设为正值（如1/√d1/√d1/√d）以生成对称区间。

（2）数学解析

均匀分布初始化的数学基础是方差保持原则，旨在确保信号在神经网络各层间传播时保持方差稳定。具体推导如下：

• 均匀分布的方差 ：若权重w U(a,b)w ~ U(a, b)w U(a,b)，则其方差为：
  Var(w)=(b−a)212 \text{Var}(w) = \frac{(b - a)^2}{12} Var(w)=12(b−a)2
• 输出方差计算 ：对于线性层y=w⋅xy = w · xy=w⋅x（忽略偏置），若输入xxx的方差为Var(x)Var(x)Var(x)，则输出yyy的方差为：
  Var(y)=d⋅Var(w)⋅Var(x) \text{Var}(y) = d \cdot \text{Var}(w) \cdot \text{Var}(x) Var(y)=d⋅Var(w)⋅Var(x)
  其中，ddd为输入维度（即faninfan_{in}fanin）。
• 方差保持条件 ：为使Var(y)=Var(x)Var(y) = Var(x)Var(y)=Var(x)，需满足：
  d⋅Var(w)=1  ⟹  Var(w)=1d d \cdot \text{Var}(w) = 1 \implies \text{Var}(w) = \frac{1}{d} d⋅Var(w)=1⟹Var(w)=d1
• 区间确定 ：将方差公式代入：
  (b−a)212=1d  ⟹  b−a=23d \frac{(b - a)^2}{12} = \frac{1}{d} \implies b - a = \frac{2\sqrt{3}}{\sqrt{d}} 12(b−a)2=d1⟹b−a=d 23
  为简化计算，通常取对称区间[−c,c][-c, c][−c,c]，则：
  c=3d≈1d c = \frac{\sqrt{3}}{\sqrt{d}} \approx \frac{1}{\sqrt{d}} c=d 3 ≈d 1
  因此，实际常用区间为[−1/√d,1/√d][-1/√d, 1/√d][−1/√d,1/√d]。

（3）适用场景

1. 浅层网络 ：如多层感知机（MLP）或简单CNN，层数较少（≤3≤3≤3层），方差累积效应不显著。
2. Sigmoid/Tanh激活函数 ：这些函数在输入接近零时梯度较大，均匀分布的对称区间（如[−1/√d,1/√d][-1/√d, 1/√d][−1/√d,1/√d]）能保持输入在激活函数的线性区域。
3. 快速原型验证：实现简单，计算开销低，适合在模型设计初期快速验证结构有效性。

（4）代码示例

linear1 = nn.Linear(in_features=5, out_features=3)
nn.init.uniform_(linear1.weight)
print(f"linear1：{linear1.weight.data}")

• 代码输出：

  linear1：tensor([[0.8548, 0.3546, 0.1321, 0.9386, 0.1632],
  [0.1412, 0.6467, 0.5987, 0.4052, 0.2577],
  [0.1382, 0.1726, 0.0094, 0.3455, 0.5361]])

3.1.2 固定值初始化

（1）函数定义

torch.nn.init.constant_(tensor, value)

• 功能：将神经网络所有权重参数统一设置为特定常数值，通过人为控制参数初始状态，强制所有神经元从相同起点开始学习。
• 参数说明 ：
  • tensor ：待初始化的权重张量，通常为nn.Linear层的weight属性。例如，linear2.weight是一个形状为(out_features, in_features)的二维张量；
  • value：初始化的固定值，可为任意标量数值（如整数、浮点数）。该值直接影响训练初期的信号传播强度，典型取值为0（偏置）或小常数（如0.01）。

（2）数学解释

固定值初始化的数学本质是构造全等矩阵，其核心问题在于破坏了梯度下降的优化基础：

• 权重矩阵表示 ：若所有权重初始化为固定值ccc，则权重矩阵WWW满足：
  W=[cc⋯ccc⋯c⋮⋮⋱⋮cc⋯c]m×n W = \begin{bmatrix} c & c & \cdots & c \\ c & c & \cdots & c \\ \vdots & \vdots & \ddots & \vdots \\ c & c & \cdots & c \end{bmatrix}_{m \times n} W= cc⋮ccc⋮c⋯⋯⋱⋯cc⋮c m×n
  其中，mmm为输出维度，nnn为输入维度。
• 前向传播对称性 ：对于输入向量x=[x1,x2,...,xn]x = [x₁, x₂, ..., xₙ]x=[x1,x2,...,xn]，输出y=Wxy = Wxy=Wx的计算结果为：
  yi=c⋅∑j=1nxj(∀i∈{1,2,...,m}) y_i = c \cdot \sum_{j=1}^{n} x_j \quad (\forall i \in \{1,2,\ldots,m\}) yi=c⋅j=1∑nxj(∀i∈{1,2,...,m})
  所有输出神经元仅相差偏置项，丧失特征区分能力。
• 反向传播失效 ：损失函数LℒL对权重的梯度∇WL∇Wℒ∇WL为标量ggg（因所有权重相同），导致权重更新后仍保持对称：
  Wnew=c−η⋅g(所有元素相同) W_{\text{new}} = c - \eta \cdot g \quad \text{(所有元素相同)} Wnew=c−η⋅g(所有元素相同)
  其中，ηηη为学习率。这种对称性使模型无法学习差异化特征，陷入伪优化状态。

（3）适用场景

1. 偏置项初始化 ：几乎所有神经网络中，偏置项均应初始化为0：

   nn.init.constant_(layer.bias, 0)

2. 模型调试与验证 ：

   • 对称性测试：将权重初始化为相同值，验证梯度是否同步更新：

   nn.init.constant_(linear.weight, 0.5)

   • 数值稳定性测试：将权重初始化为极大/极小值（如1e6），检测梯度爆炸/消失。

（4）代码示例

linear2 = nn.Linear(in_features=5, out_features=3)
nn.init.constant_(linear2.weight, 5)
print(f"linear2：{linear2.weight.data}")

• 代码输出：

  linear2：tensor([[5., 5., 5., 5., 5.],
  [5., 5., 5., 5., 5.],
  [5., 5., 5., 5., 5.]])

3.1.3 全0初始化

（1）函数定义

torch.nn.init.zeros_(tensor, out=None)

• 函数功能：将输入的参数张量（如权重矩阵、偏置向量）的所有元素赋值为0，是最简单的参数初始化方式之一。
• 参数说明 ：
  • tensor：待初始化的参数张量，需为可学习参数（如linear.weight、bn.bias等），数据类型需为浮点型（如float32、float64）。
  • out：指定输出张量，若不设置则直接修改tensor本身（原地操作），通常省略此参数。

（2）代码示例

linear3 = nn.Linear(in_features=5, out_features=3)
nn.init.zeros_(linear3.weight)
print(f"linear3：{linear3.weight.data}")

• 代码输出：

  linear3：tensor([[0., 0., 0., 0., 0.],
  [0., 0., 0., 0., 0.],
  [0., 0., 0., 0., 0.]])

3.1.4 全1初始化

（1）函数定义

torch.nn.init.ones_(tensor)

• 函数功能：将输入张量（通常是模型的权重或偏置参数）的所有元素赋值为1，实现参数的全1初始化。该函数直接修改输入张量的值（原地操作），无返回值。
• 参数说明 ：
  • tensor：必选参数，类型为torch.Tensor，表示需要初始化的参数张量（如线性层的weight或bias）。需注意，张量必须是可修改的（即requires_grad=True，模型参数默认满足此条件）。

（2）代码示例

linear4 = nn.Linear(in_features=5, out_features=3)
nn.init.ones_(linear4.weight)
print(f"linear4：{linear4.weight.data}")

• 代码输出：

  linear4：tensor([[1., 1., 1., 1., 1.],
  [1., 1., 1., 1., 1.],
  [1., 1., 1., 1., 1.]])

3.1.5 正态分布初始化

（1）函数定义

torch.nn.init.normal_(tensor, mean=0.0, std=1.0)  

• 函数功能 ：通过从均值为 mean、标准差为 std 的正态分布中随机采样，为神经网络权重赋予初始值。这种初始化方法的核心思想是利用正态分布的统计特性，使权重在零附近对称分布，避免所有神经元初始状态完全相同。
• 参数说明 ：
  • tensor：待初始化的权重张量（如nn.Linear层的weight属性）。
  • mean：正态分布的均值，默认为0.0。均值决定权重分布的中心位置，通常设为0以确保权重对称。
  • std：正态分布的标准差，默认为1.0。标准差控制权重的离散程度：
    • 过小 ：如std=0.01，权重过于集中，可能导致信号逐层衰减（梯度消失）；
    • 过大 ：如 std=10，权重分散性过强，可能引发信号爆炸（梯度爆炸）；
    • 通常设为std=1/√d（d为输入维度），以保持信号方差稳定（类似Xavier初始化的方差保持原则）。

（2）数学原理

若权重w∼N(μ,σ2)w \sim \mathcal{N}(\mu, \sigma^2)w∼N(μ,σ2)，则其方差为Var(w)=σ2\text{Var}(w) = \sigma^2Var(w)=σ2。对于线性层y=w⋅xy = w \cdot xy=w⋅x（忽略偏置），输出方差为：
Var(y)=d⋅Var(w)⋅Var(x)=d⋅σ2⋅Var(x) \text{Var}(y) = d \cdot \text{Var}(w) \cdot \text{Var}(x) = d \cdot \sigma^2 \cdot \text{Var}(x) Var(y)=d⋅Var(w)⋅Var(x)=d⋅σ2⋅Var(x)

为满足方差保持条件Var(y)=Var(x)\text{Var}(y) = \text{Var}(x)Var(y)=Var(x)，需σ2=1/d\sigma^2 = 1/dσ2=1/d，即σ=1/d\sigma = 1/\sqrt{d}σ=1/d 。此时权重分布为N(0,1/d)\mathcal{N}(0, 1/d)N(0,1/d)，确保信号在层间稳定传播。

（3）代码示例

linear5 = nn.Linear(in_features=5, out_features=3)
nn.init.normal_(linear5.weight, mean=0, std=1)
print(f"linear5：{linear5.weight.data}")

• 代码输出：

  linear5：tensor([[ 1.2908e+00, 3.1431e-01, 3.1344e-01, -3.4398e-01, 9.2638e-04],
  [ 7.4909e-01, -2.7544e+00, -1.3835e+00, 4.7837e-01, 2.0643e+00],
  [-2.3407e-01, 9.9443e-01, 1.1851e+00, -1.1828e+00, -1.8222e+00]])

3.1.6 kaiming初始化（HE初始化）

（1）函数定义

torch.nn.init.kaiming_normal_(tensor, a=0, mode='fan_in', nonlinearity='relu')

torch.nn.init.kaiming_uniform_(tensor, a=0, mode='fan_in', nonlinearity='relu')

• 函数功能 ：核心是方差自适应调整。它根据输入维度fan_in（即输入神经元数量）动态计算权重分布的尺度：
  • 正态分布版本 ：权重从N(0,σ2)\mathcal{N}(0, \sigma^2)N(0,σ2)采样，标准差σ=2/fan_in\sigma = \sqrt{2 / \text{fan\_in}}σ=2/fan_in ；
  • 均匀分布版本 ：权重从U[−limit,limit]U[-\text{limit}, \text{limit}]U[−limit,limit]采样，极限值limit=6/fan_in\text{limit} = \sqrt{6 / \text{fan\_in}}limit=6/fan_in 。
• 参数说明 ：
  • tensor ：待初始化的权重张量（如nn.Linear层的weight属性），形状为(out_features, in_features)。
  • a ：激活函数负半区斜率，默认为0（适用于标准ReLU）。若使用LeakyReLU，需设置a为负斜率（如a=0.01）。
  • mode ：方差计算模式，可选'fan_in'（默认）或'fan_out'。'fan_in'基于输入维度计算方差，适合前向传播；'fan_out'基于输出维度，适合反向传播。
  • nonlinearity ：激活函数类型，默认为'relu'。支持'leaky_relu'、'selu'等，需与a参数配合。

（2）数学原理

Kaiming初始化的数学基础是方差保持原则，但针对ReLU激活函数的特性进行了修正。ReLU在负半区输出为0，导致前向传播时信号方差减半。为保持各层方差稳定，需增大权重方差。推导过程如下：

1. ReLU的方差特性
   设输入xxx的方差为Var(x)\text{Var}(x)Var(x)，权重www的方差为Var(w)\text{Var}(w)Var(w)。对于线性层y=w⋅xy = w \cdot xy=w⋅x（忽略偏置），ReLU激活后输出为：
   yReLU=max⁡(0,y) y_{\text{ReLU}} = \max(0, y) yReLU=max(0,y)
   由于ReLU在负半区输出为0，仅保留正半区信号。假设xxx和www独立且均值为0，则yyy的方差为：
   Var(y)=fan_in⋅Var(w)⋅Var(x) \text{Var}(y) = \text{fan\in} \cdot \text{Var}(w) \cdot \text{Var}(x) Var(y)=fan_in⋅Var(w)⋅Var(x)
   ReLU激活后，输出方差减半：
   Var(yReLU)=12Var(y)=12fan_in⋅Var(w)⋅Var(x) \text{Var}(y{\text{ReLU}}) = \frac{1}{2} \text{Var}(y) = \frac{1}{2} \text{fan\_in} \cdot \text{Var}(w) \cdot \text{Var}(x) Var(yReLU)=21Var(y)=21fan_in⋅Var(w)⋅Var(x)
2. 方差保持条件
   为使Var(yReLU)=Var(x)\text{Var}(y_{\text{ReLU}}) = \text{Var}(x)Var(yReLU)=Var(x)，需满足：
   12fan_in⋅Var(w)⋅Var(x)=Var(x)  ⟹  Var(w)=2fan_in \frac{1}{2} \text{fan\_in} \cdot \text{Var}(w) \cdot \text{Var}(x) = \text{Var}(x) \implies \text{Var}(w) = \frac{2}{\text{fan\_in}} 21fan_in⋅Var(w)⋅Var(x)=Var(x)⟹Var(w)=fan_in2
3. 分布参数推导
   • 正态分布 ：若w∼N(0,σ2)w \sim \mathcal{N}(0, \sigma^2)w∼N(0,σ2)，则Var(w)=σ2\text{Var}(w) = \sigma^2Var(w)=σ2。因此：
     σ2=2fan_in  ⟹  σ=2fan_in \sigma^2 = \frac{2}{\text{fan\_in}} \implies \sigma = \sqrt{\frac{2}{\text{fan\_in}}} σ2=fan_in2⟹σ=fan_in2
   • 均匀分布 ：若w∼U(a,b)w \sim U(a, b)w∼U(a,b)，则Var(w)=(b−a)212\text{Var}(w) = \frac{(b - a)^2}{12}Var(w)=12(b−a)2。设对称区间[−c,c][-c, c][−c,c]，则：
     (2c)212=2fan_in  ⟹  c=6fan_in \frac{(2c)^2}{12} = \frac{2}{\text{fan\_in}} \implies c = \sqrt{\frac{6}{\text{fan\_in}}} 12(2c)2=fan_in2⟹c=fan_in6
     因此极限值limit=6/fan_in\text{limit} = \sqrt{6 / \text{fan\_in}}limit=6/fan_in 。

（3）代码示例

## 6.1 正态分布
linear6 = nn.Linear(in_features=5, out_features=3)
nn.init.kaiming_normal_(linear6.weight)
print(f"linear6：{linear6.weight.data}")
## 6.2 均匀分布
linear7 = nn.Linear(in_features=5, out_features=3)
nn.init.kaiming_uniform_(linear7.weight)
print(f"linear7：{linear7.weight.data}")

• 代码输出：

  linear6：tensor([[ 0.2532, -0.7815, 0.8438, 0.4325, 1.1670],
  [ 0.4102, -1.1320, -0.5118, -0.2413, -0.4213],
  [ 0.5215, -0.5718, -0.3172, 0.3912, -0.3212]])
  linear7：tensor([[-0.2655, -0.3182, 0.4056, 1.0331, -0.3875],
  [-0.2089, -0.7570, -0.1558, -0.3459, -0.8596],
  [ 0.0360, 0.3972, -0.5948, -0.8340, 1.0546]])

3.1.7 xavier初始化（Glorot初始化）

（1）函数定义

torch.nn.init.xavier_normal_(tensor, gain=1.0)

torch.nn.init.xavier_uniform_(tensor, gain=1.0)

• 函数功能 ：
  • xavier_normal_：从均值为0、标准差为σ\sigmaσ的截断正态分布中采样权重。标准差σ\sigmaσ的计算基于输入和输出维度。
  • xavier_uniform_：从[−a,a][-a, a][−a,a]的均匀分布中采样权重。区间边界aaa的计算同样基于输入和输出维度。
• 参数说明 ：
  • tensor ：待初始化的权重张量，通常是nn.Linear层的weight属性，形状为(out_features, in_features)。
  • gain：可选的缩放因子，用于调整权重分布的尺度。其值取决于激活函数的类型。

（2）数学原理

Xavier初始化的数学基础是方差保持原则，它同时考虑了前向传播和反向传播中的信号方差稳定性。

1. 方差保持目标
   • 前向传播 ：对于线性层y=Wxy = Wxy=Wx，若输入xxx的方差为Var(x)\text{Var}(x)Var(x)，权重WWW的方差为Var(W)\text{Var}(W)Var(W)，则输出yyy的方差为：
     Var(y)=fan_in⋅Var(W)⋅Var(x) \text{Var}(y) = \text{fan\_in} \cdot \text{Var}(W) \cdot \text{Var}(x) Var(y)=fan_in⋅Var(W)⋅Var(x)
     其中，fan_in\text{fan\_in}fan_in是输入维度。
   • 反向传播 ：在反向传播中，梯度δx\delta_xδx通过权重WWW传播，其方差为：
     Var(δx)=fan_out⋅Var(W)⋅Var(δy) \text{Var}(\delta_x) = \text{fan\_out} \cdot \text{Var}(W) \cdot \text{Var}(\delta_y) Var(δx)=fan_out⋅Var(W)⋅Var(δy)
     其中，fan_out\text{fan\_out}fan_out是输出维度。
2. 方差平衡条件
   为同时满足前向和反向传播的方差稳定（即Var(y)=Var(x)\text{Var}(y) = \text{Var}(x)Var(y)=Var(x)且Var(δx)=Var(δy)\text{Var}(\delta_x) = \text{Var}(\delta_y)Var(δx)=Var(δy)），Xavier提出取fan_in\text{fan\_in}fan_in和fan_out\text{fan\_out}fan_out的平均值：
   Var(W)=2fan_in+fan_out \text{Var}(W) = \frac{2}{\text{fan\_in} + \text{fan\_out}} Var(W)=fan_in+fan_out2
3. 分布参数推导
   • 正态分布 ：若权重W∼N(0,σ2)W \sim \mathcal{N}(0, \sigma^2)W∼N(0,σ2)，则Var(W)=σ2\text{Var}(W) = \sigma^2Var(W)=σ2。因此：
     σ2=2fan_in+fan_out  ⟹  σ=2fan_in+fan_out \sigma^2 = \frac{2}{\text{fan\_in} + \text{fan\_out}} \implies \sigma = \sqrt{\frac{2}{\text{fan\_in} + \text{fan\_out}}} σ2=fan_in+fan_out2⟹σ=fan_in+fan_out2
   • 均匀分布 ：若权重W∼U(−a,a)W \sim U(-a, a)W∼U(−a,a)，则Var(W)=a23\text{Var}(W) = \frac{a^2}{3}Var(W)=3a2。因此：
     a23=2fan_in+fan_out  ⟹  a=6fan_in+fan_out \frac{a^2}{3} = \frac{2}{\text{fan\_in} + \text{fan\_out}} \implies a = \sqrt{\frac{6}{\text{fan\_in} + \text{fan\_out}}} 3a2=fan_in+fan_out2⟹a=fan_in+fan_out6

（3）代码示例

## 7.1 正态分布
linear8 = nn.Linear(in_features=5, out_features=3)
nn.init.xavier_normal_(linear8.weight)
print(f"linear8：{linear8.weight.data}")
## 7.2 均匀分布
linear9 = nn.Linear(in_features=5, out_features=3)
nn.init.xavier_uniform_(linear9.weight)
print(f"linear9：{linear9.weight.data}")

• 代码输出：

  linear8：tensor([[ 0.6452, -0.0405, -0.8916, -0.4812, -0.3993],
  [ 0.0948, 0.3321, -0.0952, 0.4087, -0.2104],
  [-0.0165, 0.0839, -0.2089, 0.0098, 0.2370]])
  linear9：tensor([[-0.6624, -0.1772, -0.8013, -0.0340, 0.5587],
  [ 0.3718, 0.5098, 0.7073, -0.0485, 0.5517],
  [-0.7382, -0.6923, 0.4948, 0.5596, -0.5952]])

3.2 选择方式

在深度学习实践中，参数初始化并非"一刀切"的流程，而是一个需要根据网络结构、激活函数和任务特性进行权衡的决策过程。选择合适的初始化方法，能显著提升模型的训练速度、稳定性和最终性能。

3.2.1 核心决策依据------激活函数类型

激活函数的特性是决定初始化方法的首要因素，因为它直接影响信号在前向和反向传播中的方差变化。

（1）Sigmoid/Tanh 激活函数→Xavier 初始化

1. 适用场景：当网络主要使用Sigmoid或Tanh等饱和型激活函数时。
2. 选择理由：Sigmoid和Tanh函数在输入接近 0 时近似线性，且输出范围以 0 为中心对称（Tanh尤其如此）。Xavier初始化通过平衡输入和输出维度的方差，确保信号在层间传递时保持稳定，避免了因方差过大或过小导致的信号饱和（梯度消失）或爆炸。

（2）ReLU 及其变体→Kaiming 初始化

1. 适用场景：当网络主要使用ReLU、LeakyReLU、PReLU等修正线性单元时。这是现代深度学习，尤其是计算机视觉领域的绝对主流。
2. 选择理由 ：ReLU 函数在负半区输出为0，这会导致在前向传播中，每经过一层ReLU，信号的方差大约减半。Kaiming初始化通过将权重方差加倍（即Var(w)=2/fan_in\text{Var}(w) = 2 / \text{fan\_in}Var(w)=2/fan_in），精确地补偿了这一方差损失，保证了信号在深层网络中的稳定流动。

3.2.2 辅助考量因素------网络深度与结构

（1）浅层网络

1. 特点：对于层数较少（如 3 层以内）的简单网络，方差累积效应不显著。
2. 选择策略 ：即使使用简单的正态分布（mean=0, std=0.01）或均匀分布初始化，模型通常也能正常训练。但为了获得更稳定的起点，仍推荐遵循激活函数原则（ReLU用Kaiming，Tanh用Xavier）。

（2）深层网络

1. 特点：当网络层数加深（如超过10层），初始化的影响被指数级放大。错误的初始化几乎必然导致梯度消失或爆炸，使模型无法学习。
2. 选择策略：必须严格遵循激活函数与初始化方法的匹配原则。对于深层网络，正确的初始化不是"优化项"，而是"必需项"。Kaiming和Xavier初始化正是为解决深层网络的训练难题而设计的。

3.3.3 决策总结与黄金法则

1. 第一步：检查激活函数
   • 如果主要使用ReLU /LeakyReLU →优先选择Kaiming初始化（或直接使用PyTorch默认设置）。
   • 如果主要使用Sigmoid /Tanh →必须使用Xavier初始化。
2. 第二步：评估网络深度
   • 深层网络：严格遵守第一步的匹配原则，这是模型能否收敛的关键。
   • 浅层网络：遵守第一步是良好实践，但即使不严格匹配，风险也较小。
3. 第三步：特殊情况处理
   • 自定义层：若实现了自定义的层结构，需要为其权重手动选择合适的初始化方法。
   • 特殊激活函数 ：如SELU，需配合"自归一化"初始化（nn.init.normal_配合特定参数）。

黄金法则 ：在不确定时，对于现代深度学习模型，默认使用Kaiming初始化通常是最安全、最有效的选择。选对初始化，等于为深度学习模型的高速训练铺平了第一段路。

四、神经网络的搭建

神经网络的搭建是深度学习实践的核心环节，它将抽象的数学模型转化为可执行的计算机程序。在PyTorch中，这一过程被设计得直观而模块化，如同用乐高积木搭建复杂结构。我们只需定义好每一块"积木"（网络层）并规划好它们的连接方式（数据流向），框架便会自动处理复杂的计算，如梯度计算和参数更新。

4.1 模型搭建

模型搭建的本质是层堆叠，即将多个功能不同的网络层按特定顺序组合起来，形成一个能够处理数据并输出预测结果的完整结构。

4.1.1 模型搭建的方法

在PyTorch中，所有自定义的神经网络模型都必须继承自基础类torch.nn.Module。这个基类为您的模型提供了许多核心功能，例如参数跟踪、模型保存/加载以及GPU迁移等。搭建一个模型，我们必须实现两个关键方法：

1. __init__(self) 方法（构造函数）：
   • 功能 ：这是模型的"设计蓝图"阶段。在此方法中，我们需要定义模型将包含的所有网络层结构（如全连接层nn.Linear、卷积层nn.Conv2d等），并为它们命名（如self.layer1）。
   • 关键操作 ：除了定义层，这里也是进行参数初始化的最佳位置。我们可以调用torch.nn.init模块下的函数（如nn.init.kaiming_normal_）来覆盖PyTorch的默认初始化，为特定层设置更合适的初始权重，从而优化训练起点。
2. forward(self, x) 方法（前向传播）：
   • 功能 ：这是模型的"数据加工流水线"。它定义了当输入数据x传入模型后，如何依次流经您在__init__中定义的各个层。
   • 关键操作 ：在此方法中，我们将数据从一个层传递到下一个层，并在中间应用激活函数（如torch.relu）或其他操作。

4.1.2 模型搭建的设计

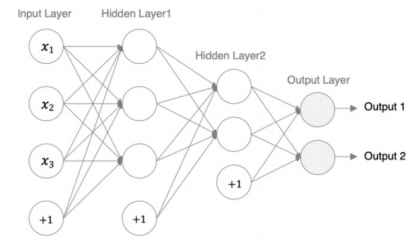
模型设计是一个融合了理论与实践的艺术，它决定了模型的学习能力和上限。一个优秀的设计需要考虑激活函数、初始化方法以及网络深度等因素的协同作用。

1. 第1个隐层（经典设计） ：
   • 激活函数 ：使用Sigmoid。这是一个早期的经典激活函数，其输出在(0, 1)之间，适合用于需要概率输出的场景或作为网络的"温和"启动。
   • 权重初始化 ：采用Xavier初始化。因为Sigmoid函数在输入接近0时梯度最大，Xavier初始化能将初始输入控制在激活函数的线性高梯度区域，有效缓解梯度消失问题，是Sigmoid/Tanh的理想搭档。
2. 第2个隐层（现代设计） ：
   • 激活函数 ：使用ReLU（修正线性单元）。这是当前最主流的激活函数，计算简单且能有效缓解梯度消失，加速模型收敛。
   • 权重初始化 ：采用He初始化。由于ReLU在负半区输出为0，会导致信号方差减半。He初始化通过增大初始权重方差来补偿这一损失，确保信号在深层网络中稳定传播，是ReLU及其变体的"黄金搭档"。
3. 输出层（任务适配） ：
   • 功能：一个简单的线性层，用于将上一层的高级特征映射到最终的输出空间。
   • 数据归一化 ：对于二分类或多分类任务，通常在线性层后接Softmax函数。它能将原始输出分数转换为概率分布，使得每个类别的预测值都在[0, 1]之间且总和为1，便于理解和使用。

4.2 参数计算

理解模型的参数数量是评估模型复杂度和潜在过拟合风险的重要一步。参数是模型在训练过程中需要学习的变量，主要包括权重和偏置。

4.2.1 核心概念

必须明确区分输入数据和网络权重。输入数据是模型的"原材料"，其形状通常是(batch_size, in_features)；而网络权重是模型内部的"可调节旋钮"，其形状由层的定义决定。初学者常将二者混淆，但它们是性质完全不同的两个概念。

4.2.2 计算方法

以一个全连接层nn.Linear(in_features=3, out_features=3)为例：

• 权重矩阵 ：形状为(out_features, in_features)，即(3, 3)，包含 3 × 3 = 9 个参数。
• 偏置向量 ：形状为(out_features)，即(3)，包含 3 个参数。
• 总参数 ：该层总参数为 9 (权重) + 3 (偏置) = 12 个。

4.3 代码示例

import torch
import torch.nn as nn
from torchsummary import summary

class model(nn.Module):
    # init 定义层
    def __init__(self):
        super().__init__()
        self.layer1 = nn.Linear(in_features=3, out_features=3)
        nn.init.kaiming_normal_(self.layer1.weight)
        self.layer2 = nn.Linear(in_features=3, out_features=2)
        nn.init.xavier_uniform_(self.layer2.weight)
        self.out = nn.Linear(in_features=2, out_features=2)
        nn.init.uniform_(self.out.weight)

    # forward 定义前向传播
    def forward(self, x):
        x_layer1 = self.layer1(x)
        x_layer1 = torch.sigmoid(x_layer1)
        x_layer2 = self.layer2(x_layer1)
        x_layer2 = torch.relu(x_layer2)
        out = self.out(x_layer2)
        out = torch.softmax(out, dim=-1)
        return out

if __name__ == '__main__':
    my_model = model()
    x = torch.randn(10, 3)
    out = my_model(x)
    print(out.shape)

    summary(my_model, input_size=(3,), batch_size=8, device='cpu')

    for name, param in my_model.named_parameters():
        print(name)
        print(param)

• 代码输出：

  torch.Size([10, 2])

        Layer (type)               Output Shape         Param #

  ================================================================
  Linear-1 [8, 3] 12
  Linear-2 [8, 2] 8
  Linear-3 [8, 2] 6

  Total params: 26
  Trainable params: 26
  Non-trainable params: 0

  Input size (MB): 0.00
  Forward/backward pass size (MB): 0.00
  Params size (MB): 0.00
  Estimated Total Size (MB): 0.00

  layer1.weight
  Parameter containing:
  tensor([[ 1.6363, 1.0848, 0.7336],
  [ 0.8740, -0.2020, 0.6790],
  [ 1.3789, -0.3659, 0.1120]], requires_grad=True)
  layer1.bias
  Parameter containing:
  tensor([-0.0126, 0.3889, 0.5600], requires_grad=True)
  layer2.weight
  Parameter containing:
  tensor([[ 0.2384, -1.0649, 0.0578],
  [-0.3475, -0.9680, 0.8144]], requires_grad=True)
  layer2.bias
  Parameter containing:
  tensor([0.5409, 0.2066], requires_grad=True)
  out.weight
  Parameter containing:
  tensor([[0.4286, 0.6680],
  [0.4187, 0.9268]], requires_grad=True)
  out.bias
  Parameter containing:
  tensor([-0.6212, -0.7025], requires_grad=True)

五、损失函数

损失函数是深度学习模型的"指南针"与"裁判"，它量化了模型预测结果与真实标签之间的差距，为模型的优化指明了方向。在训练过程中，模型的目标就是通过调整内部参数，不断减小这个差距，即最小化损失函数的值。一个设计得当的损失函数，是模型能够有效学习并最终达到高性能的关键。

5.1 定义

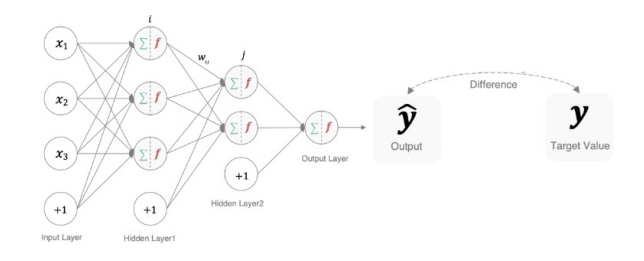
损失函数（Loss Function）是一个非负实值函数，其核心作用是评估模型预测的好坏。它接收模型的输出和真实标签作为输入，输出一个标量损失值。这个值越大，表示模型的预测越糟糕；值越小，表示预测越接近真实情况。整个训练过程，本质上就是一个以最小化损失函数为目标的优化问题。

5.2 命名

在深度学习文献和代码库中，你可能会遇到以下几种不同的名称，它们在多数情况下可以互换使用，但有时也存在细微差别：

• 损失函数：通常指代单个训练样本或一个小批量数据上的误差。
• 代价函数：通常指代整个训练集（或一个完整批次）上损失函数的平均值或总和，是模型需要全局优化的目标。
• 目标函数：一个更广义的术语，在优化问题中，它既可以是需要最小化的代价函数，也可以是需要最大化的函数（如似然函数）。
• 误差函数：与损失函数基本同义，强调模型预测值与真实值之间的"误差"。

5.3 对于多分类任务

当模型需要从三个或更多个互斥的类别中做出选择时（例如，识别一张图片是猫、狗还是鸟），我们需要一个能够衡量概率分布差异的损失函数。交叉熵损失正是为此而生，它不仅是深度学习多分类任务的标准选择，更因其优秀的数学特性而备受青睐。

5.3.1 核心思想

交叉熵损失的核心思想是如果模型为正确类别分配了高概率，就应该给予低惩罚（低损失）；反之，则给予高惩罚（高损失）。

5.3.2 数学原理

其数学公式为：
L=−∑i=1nyilog⁡(S(fθ(xi))) \mathcal{L} = - \sum_{i=1}^{n} \mathbf{y}i \log(S(f\theta(\mathbf{x}_i))) L=−i=1∑nyilog(S(fθ(xi)))

1. 模型原始输出fθ(xi)f_\theta(\mathbf{x}_i)fθ(xi)：这是神经网络最后一层的直接输出，通常被称为Logits。它是一组未经过处理的原始分数，可以是任意实数，大小并不直接代表概率。
2. Softmax函数 S(⋅)S(\cdot)S(⋅) ：这是将原始分数转换为有效概率分布的"魔法棒"。它分两步工作：
   • 指数化 ：对所有Logits取指数（exe^xex），确保所有值都为正；
   • 归一化：将指数化后的值除以它们的总和，使得所有类别的概率值相加正好等于1。
3. 真实标签 yi\mathbf{y}_iyi ：在多分类任务中，真实标签通常采用One-Hot（独热）编码。这种编码方式非常纯粹地表达了这个是，那些都不是的语义。
4. 负对数似然 −log⁡(⋅)-\log(\cdot)−log(⋅) ：这是实现"奖惩分明"的关键。观察函数f(p)=−log⁡(p)f(p) = -\log(p)f(p)=−log(p)：
   • 当正确类别的预测概率ppp接近1时，−log⁡(p)-\log(p)−log(p)接近0，意味着损失极小，模型做得很好；
   • 当ppp接近0时，−log⁡(p)-\log(p)−log(p)趋向于无穷大，意味着损失巨大，模型犯了大错。

5.3.3 代码示例

# （1）标签
# y_true1 = torch.tensor([0, 1, 2], dtype=torch.int64)
# （2）one-hot
y_true1 = torch.tensor([[1, 0, 0], [0, 1, 0], [0, 0, 1]], dtype=torch.float32)

y_pred1 = torch.tensor([[18, 9, 10], [2, 14, 6], [3, 8, 16]], dtype=torch.float32)

loss1 = nn.CrossEntropyLoss()
print(loss1(y_pred1, y_true1))

• 代码输出：

  tensor(0.0004)

5.4 对于二分类任务

当模型需要解决的是"是或否"的问题时，例如判断一封邮件是否为垃圾邮件、一张图片是否包含猫，我们就进入了二分类任务的领域。针对这类问题，二元交叉熵损失是衡量模型表现最常用且最有效的工具。它精确地量化了模型预测的概率与真实标签（0或1）之间的差距。

5.4.1 计算方式

二元交叉熵损失的数学公式看似简洁，却蕴含着深刻的优化逻辑：
L=−ylog⁡y^−(1−y)log⁡(1−y^) L = -y \log \hat{y} - (1 - y) \log (1 - \hat{y}) L=−ylogy^−(1−y)log(1−y^)

这个公式实际上是一个"智能开关"，会根据真实标签yyy的值自动选择计算方式：

1. 当真实标签y=1y=1y=1时（即样本属于正类） ：公式简化为L=−log⁡(y^)L = -\log(\hat{y})L=−log(y^)，此时，损失函数只关注模型对正类的预测概率y^\hat{y}y^。
   • 如果模型预测y^\hat{y}y^接近1（例如0.99），表示模型非常确信这是正类，且预测正确。此时−log⁡(0.99)-\log(0.99)−log(0.99)是一个非常小的正数，损失极低；
   • 如果模型预测y^\hat{y}y^接近0（例如0.01），表示模型错误地认为这几乎不可能是正类。此时−log⁡(0.01)-\log(0.01)−log(0.01)是一个巨大的正数，损失极高，模型会受到严厉的惩罚。
2. 当真实标签y=0y=0y=0时（即样本属于负类） ：公式简化为L=−log⁡(1−y^)L = -\log(1 - \hat{y})L=−log(1−y^)，此时，损失函数关注的是模型对负类的预测概率，即1−y^1 - \hat{y}1−y^。
   • 如果模型预测y^\hat{y}y^接近0（例如0.01），表示模型非常确信这是负类，预测正确。此时1−y^1 - \hat{y}1−y^接近1，−log⁡(1−y^)-\log(1 - \hat{y})−log(1−y^)是一个很小的正数，损失极低；
   • 如果模型预测y^\hat{y}y^接近1（例如0.99），表示模型大错特错，把负类当成了正类。此时1−y^1 - \hat{y}1−y^接近0，−log⁡(1−y^)-\log(1 - \hat{y})−log(1−y^)是一个巨大的正数，损失极高。

5.4.2 代码示例

y_true2 = torch.tensor([0, 1, 0, 1], dtype=torch.float32)
y_pred2 = torch.tensor([0.1, 0.9, 0.2, 0.8], dtype=torch.float32)

loss2 = nn.BCELoss()
print(loss2(y_pred2, y_true2))

• 代码输出：

  tensor(0.1643)

5.5 对于回归任务

5.5.1 MAE函数

平均绝对误差（Mean Absolute Error, MAE）是回归任务中最直观、最基础的损失函数之一。它衡量的是模型预测值与真实值之间绝对差异的平均值，如同用一把尺子测量预测值平均偏离了真实值多远。

（1）数学原理

MAE的数学公式简洁明了：
L=1n∑i=1n∣yi−fθ(xi)∣ \mathcal{L} = \frac{1}{n} \sum_{i=1}^{n} |y_i - f_\theta(x_i)| L=n1i=1∑n∣yi−fθ(xi)∣

这个公式的核心思想可以通俗地理解为：

• ∣yi−fθ(xi)∣|y_i - f_\theta(x_i)|∣yi−fθ(xi)∣：计算单个样本的绝对误差。假设真实房价是30万，模型预测了32万，误差就是2万；如果预测了28万，误差也是2万。MAE不关心预测是偏高还是偏低，只关心偏离的绝对大小。
• 1n∑\frac{1}{n} \sumn1∑：将所有样本的绝对误差进行求和并取平均，得到整个批次的平均损失。

这个公式保证了损失值永远是非负的，并且当模型预测得越准（绝对误差越小），损失值就越低。

（2）可视化表示

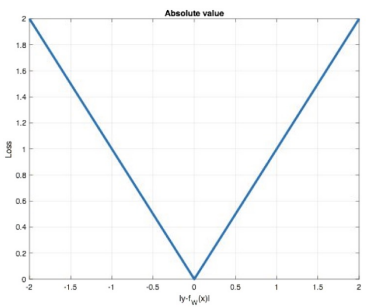
MAE的损失函数图像是一个经典的"V"形，其顶点在原点(0,0)。

• 线性关系：图像清晰地表明，损失与误差之间是线性关系。无论误差是1还是100，损失都稳定地按比例增长。
• 恒定斜率：在误差不为零的区域，斜率恒定为±1。这意味着，无论当前误差有多大，模型为了减少损失而进行的参数调整的"力度"都是相同的。这种特性使得MAE对异常值不敏感，因为一个极大的误差不会不成比例地主导整个损失。

（3）定义

MAE也被称为L1 Loss ，它以绝对误差作为衡量预测值与真实值之间"距离"的标尺。

L1范数距离：在数学上，它对应着向量空间的L1范数，也常被形象地称为"曼哈顿距离"。想象你在纽约曼哈顿，从一个街区到另一个街区，你不能直接穿楼而过，只能沿着街道走。你走过的总路程就是所有南北向距离和东西向距离的绝对值之和。MAE就是这样计算预测与真实值之间的"街区距离"。

（4）特点

MAE的特点非常鲜明，使其在特定场景下具有不可替代的优势：

1. 稀疏性与正则化：由于其恒定的梯度特性，MAE在优化过程中倾向于产生稀疏的解。这意味着它更倾向于将一些不重要的特征权重直接推向0。因此，MAE常常被巧妙地作为正则项（即L1正则化）添加到其他损失函数中，用于惩罚模型的复杂度，有效防止过拟合，鼓励模型学习更简单、更关键的特征。
2. 零点不平滑：这是MAE最主要的缺点。从"V"形图可以看出，在误差为0的顶点处，函数是不可导的，存在一个尖角。这会导致梯度下降算法在接近最优解时可能"刹不住车"，因为梯度在零点附近是恒定的，模型可能会在最小值附近来回震荡，甚至"跳过"最优点，从而影响收敛的精度。

（5）代码示例

y_true3_1 = torch.tensor([2.0, 3.0, 1.0], dtype=torch.float32)
y_pred3_1 = torch.tensor([1.0, 5.0, 4.0], dtype=torch.float32)

loss3_2 = nn.MSELoss()
print(loss3_2(y_pred3_1, y_true3_1))

• 代码输出：

  tensor(4.6667)

5.5.2 MSE函数

均方误差（Mean Squared Error, MSE）是回归任务中最经典、最广泛使用的损失函数。它通过计算预测值与真实值之间差值的平方，来衡量模型的预测精度。由于其优秀的数学特性，MSE在许多场景下都是首选的损失函数。

（5）代码示例

在PyTorch中，使用 nn.MSELoss 可以轻松实现MSE计算。（注意：参考信息中的代码示例有误，此处已修正）

import torch
import torch.nn as nn
# 真实值
y_true = torch.tensor([2.0, 3.0, 1.0], dtype=torch.float32)
# 模型预测值
y_pred = torch.tensor([1.0, 5.0, 4.0], dtype=torch.float32)
# 实例化MSE损失函数
mse_loss_fn = nn.MSELoss()
# 计算损失
loss_value = mse_loss_fn(y_pred, y_true)
print(loss_value)

• 代码解析 ：
  • 代码首先定义了真实值 y_true 和预测值 y_pred。
  • nn.MSELoss() 创建了一个MSE损失函数的实例。
  • loss_value 的计算结果为 tensor(4.6667)。
• 输出解读 ：
  • 这个结果是通过公式 ( (2-1)² + (3-5)² + (1-4)² ) / 3 计算得出的，即 (1 + 4 + 9) / 3 = 14 / 3 ≈ 4.6667。
  • 它直观地告诉我们，模型在这三个样本上的平均平方误差约为4.67。这个数值比MAE计算的2.0要大，这是因为MSE对误差为3的样本（(1-4)²=9）给予了更大的权重。在训练过程中，我们的目标就是通过调整模型参数，让这个值不断减小。

---

以上内容由AI生成，仅供参考和借鉴

（1）数学原理

MSE的数学公式直观且强大：
L=1n∑i=1n(yi−fθ(xi))2 \mathcal{L} = \frac{1}{n} \sum_{i=1}^{n} (y_i - f_\theta(x_i))^2 L=n1i=1∑n(yi−fθ(xi))2

这个公式的核心思想可以通俗地理解为：

• (yi−fθ(xi))2(y_i - f_\theta(x_i))^2(yi−fθ(xi))2 ：计算单个样本的平方误差。假设真实房价是30万，模型预测了32万，误差是2万，平方后就是4万；如果预测了28万，误差也是2万，平方后同样是4万。MSE不关心预测的方向，只关心偏离的大小，并且通过平方运算放大了大误差的影响。
• 1n∑\frac{1}{n} \sumn1∑ ：将所有样本的平方误差进行求和并取平均，得到整个批次的平均损失。

这个公式保证了损失值永远是非负的，并且当模型预测得越准（误差越小），损失值就越低。平方运算使得MSE对误差的变化非常敏感。

（2）可视化表示

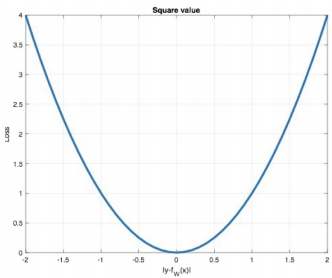
MSE的损失函数图像是一个经典的抛物线，其顶点在原点(0,0)。

• 二次的关系：图像清晰地表明，损失与误差之间是二次关系。这意味着误差越大，损失的增长速度会急剧加快。
• 变化的斜率：在误差不为零的区域，斜率随着误差的增大而增大。例如，当误差为1时，斜率为2；当误差为10时，斜率就变成了20。这种特性使得MSE对大误差的样本给予极大的惩罚，迫使模型优先关注那些预测得非常糟糕的样本。

（3）定义

MSE也被称为L2 Loss，它以误差的平方和的均值作为衡量预测值与真实值之间"距离"的标尺。

L2范数距离：在数学上，它对应着向量空间的L2范数，也常被形象地称为"欧氏距离"。想象你在二维平面上，从一个点到另一个点的直线距离就是欧氏距离。MSE计算的就是预测值与真实值在这个多维空间中的"直线距离"的平方的平均值。

（4）特点

MSE的特点使其在大多数回归任务中表现出色，但也存在一些需要注意的方面：

1. 可导性与优化友好：MSE的损失函数图像是一个处处光滑的抛物线，在每一点都是可导的。这使得基于梯度的优化算法（如梯度下降）能够非常稳定、高效地工作，特别是在接近最优解时，梯度会逐渐变小，有助于模型精细地收敛到最小值。
2. 对大误差敏感与梯度爆炸 ：这是MSE最主要的缺点。由于平方项的存在，一个误差极大的样本（异常值）会对总损失产生不成比例的巨大影响。这不仅可能导致模型过度拟合这些异常值，更严重的是，在反向传播时，大误差会导致梯度过大，可能引发梯度爆炸问题，使得训练过程变得不稳定甚至崩溃。

（5）代码示例

y_true3_1 = torch.tensor([2.0, 3.0, 1.0], dtype=torch.float32)
y_pred3_1 = torch.tensor([1.0, 5.0, 4.0], dtype=torch.float32)
loss3_1 = nn.L1Loss()
print(loss3_1(y_pred3_1, y_true3_1))

• 代码输出：

  tensor(2.)

5.5.3 smooth L1函数

Smooth L1损失，也常被称为Huber Loss，是一种在回归任务中极具智慧的损失函数。它并非凭空创造，而是为了解决MAE（L1 Loss）和MSE（L2 Loss）各自固有的缺陷而设计的"混合体"，旨在汲取两者的精华，实现性能与稳定性的最佳平衡。

（1）数学表示

Smooth L1的数学定义是一个巧妙的分段函数，它根据误差的大小动态地切换计算方式：
smoothL1(x)={0.5x2if ∣x∣<1∣x∣−0.5otherwise \text{smooth}_{L_1}(x) = \begin{cases} 0.5x^2 & \text{if } |x| < 1 \\ |x| - 0.5 & \text{otherwise} \end{cases} smoothL1(x)={0.5x2∣x∣−0.5if ∣x∣<1otherwise

其中，xxx代表预测值与真实值之间的误差（x=fθ(x)−yx = f_\theta(x) - yx=fθ(x)−y）。

这个公式的核心思想可以通俗地理解为：

• 当误差较小时（∣x∣<1|x| < 1∣x∣<1） ：函数采用0.5x20.5x^20.5x2的形式，这与MSE（L2 Loss）的计算方式几乎一致（差一个常数系数0.5）。
• 当误差较大时（∣x∣≥1|x| \ge 1∣x∣≥1） ：函数切换为∣x∣−0.5|x| - 0.5∣x∣−0.5的形式，这与MAE（L1 Loss）的计算方式非常相似（同样差一个常数-0.5）。

这种"看人下菜"的策略，使得Smooth L1能够根据预测的准确程度，自适应地选择最合适的惩罚机制。

（2）可视化表示

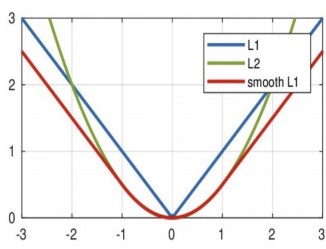
Smooth L1的损失函数图像是其数学特性的完美视觉呈现，它像一个被精心打磨过的"V"字形。

• 中心区域（二次曲线） ：在误差区间 [-1, 1] 内，图像是一条平滑的抛物线。这对应着MSE的特性，保证了在接近最优解时，函数是光滑且可导的。
• 外部区域（直线）：在误差区间之外，图像变成了两条笔直的斜线。这对应着MAE的特性，保证了在误差较大时，损失线性增长，梯度恒定。

从抛物线到直线的过渡是平滑的，没有MAE在零点处的尖角，也没有MSE无限延伸的陡峭曲线。这个图像直观地展示了Smooth L1如何巧妙地融合了两种损失函数的几何形态。

（3）定义

Smooth L1损失，从本质上讲，是对L1损失进行的光滑化改进。它通过引入一个阈值（在PyTorch中默认为1），构建了一个在L1和L2损失之间无缝切换的混合模型。其设计哲学是：在预测接近真实值时，我们关心收敛的精度和稳定性；在预测偏离真实值较远时，我们更关心对异常值的鲁棒性。Smooth L1正是这一哲学的数学实现，它在不同误差范围内表现出不同的行为，从而成为一个更加全面和稳健的损失函数。

（4）特点

Smooth L1的特点非常突出，它精准地打击了MAE和MSE各自的"软肋"，是理论与实践结合的典范：

1. 解决L1的不光滑问题：纯MAE在误差为零的点存在一个不可导的尖角，这会导致梯度不连续，可能使优化器在接近最优解时"跳过"最小值，难以精确收敛。Smooth L1通过在零点附近使用L2的二次函数，创造了一个平滑、可导的区域。这使得梯度下降算法能够稳定地、精确地收敛到最优解，避免了MAE的收敛难题。
2. 解决L2的梯度爆炸问题：纯MSE的梯度与误差成正比。当数据中存在异常值（误差极大的样本）时，会产生巨大的梯度，可能导致训练过程不稳定甚至崩溃，这就是所谓的"梯度爆炸"。Smooth L1通过在误差较大时切换到L1的线性函数，将梯度的大小限制在一个常数上（即梯度的绝对值为1）。这就像给梯度加了一个"安全阀"，有效防止了异常值引发的梯度爆炸，使模型训练更加稳健。

（5）代码示例

y_true3_1 = torch.tensor([2.0, 3.0, 1.0], dtype=torch.float32)
y_pred3_1 = torch.tensor([1.0, 5.0, 4.0], dtype=torch.float32)

loss3_3 = nn.SmoothL1Loss()
print(loss3_3(y_pred3_1, y_true3_1))

• 代码输出：

  tensor(1.5000)

六、网络优化

6.1 梯度下降算法

梯度下降算法是深度学习模型训练的基石，是驱动模型参数不断优化的核心引擎。它的根本任务是在一个复杂的多维空间中，寻找损失函数的最小值，从而让模型的预测尽可能接近真实情况。可以将其想象成一个蒙着眼睛在山中寻找山谷最低点的徒步者，他唯一能做的就是感知脚下地面的坡度，并沿着最陡峭的下坡方向前进。

6.1.1 定义

从本质上讲，梯度下降是一种迭代优化算法 ，用于寻找一个函数的最小值。在深度学习中，这个函数就是我们前面提到的损失函数 。其核心思想源于一个直观的数学原理：函数在某一点的梯度方向，是函数值在该点增长最快的方向。因此，如果我们想最小化函数值，只需要朝着梯度的反方向移动即可。这个"走一步"的过程，就是一次参数更新；通过成千上万次这样的小步更新，模型参数便能逐步逼近最优解，即损失函数的全局或局部最小值。

6.1.2 数学原理

梯度下降的参数更新规则可以用一个简洁而强大的公式来描述：
Wijnew=Wijold−η∂E∂Wij W_{ij}^{new} = W_{ij}^{old} - \eta \frac{\partial E}{\partial W_{ij}} Wijnew=Wijold−η∂Wij∂E

这个公式是整个优化过程的数学核心，逐一拆解其内涵：

• WijoldW_{ij}^{old}Wijold：代表模型中第iii个神经元与第jjj个输入连接的当前权重。这是徒步者当前所在的位置。
• ∂E∂Wij\frac{\partial E}{\partial W_{ij}}∂Wij∂E：代表损失函数EEE对该权重WijW_{ij}Wij的偏导数，也就是梯度。它量化了如果稍微改变这个权重，损失值会变化多少，即当前所在位置的"坡度"。
• η\etaη (eta)：即学习率，这是一个至关重要的超参数，它控制着每次更新参数时"迈出的步子"有多大。
• WijnewW_{ij}^{new}Wijnew：代表更新后的新权重。这是徒步者迈出一步后到达的新位置。

学习率的权衡是梯度下降算法成败的关键：

• 学习率过小：如同徒步者每次只挪动一厘米。虽然方向正确，但下山速度极慢，训练过程会非常耗时，甚至可能陷入局部最小值而无法跳出。
• 学习率过大：如同徒步者试图一步跨过整个山谷。他可能会直接跳到对面的山坡上，甚至越过最低点，导致损失值不减反增，使得模型完全无法收敛。

6.1.3 可视化表示

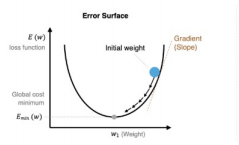
• 简单场景：在一个类似碗状的、光滑的损失函数图像中，梯度下降的路径会像一个小球从碗壁滚向碗底。它开始时下降速度快，随着坡度变缓，速度也逐渐减慢，最终稳定地停在最低点。

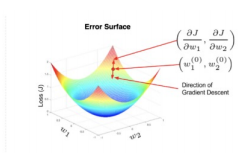
• 复杂场景：在一个充满起伏、有多个山谷和鞍点的复杂地形图中，梯度下降的路径会更加曲折。它可能会陷入一个小的山谷（局部最小值），或者在一个平坦的山脊（鞍点）上停滞不前。这些可视化直观地揭示了梯度下降算法面临的挑战，如局部最优和鞍点问题，也凸显了引入更高级优化算法（如动量法）的必要性。

6.1.4 基础概念

在实践训练中，我们通常不会一次性用所有数据来计算梯度并更新模型，而是采用分批处理的方式。这就引出了三个紧密相关的基础概念：

• Epoch（训练轮次） ：当模型完整地学习了训练集中的所有样本一次，就称为完成了一个Epoch。这相当于学生为了备考，把整本教科书从头到尾复习了一遍。
• Batch Size（批次大小） ：这是指在计算一次梯度并更新模型时，所使用的样本数量。我们不会让模型看完所有书再做一道题，而是每次只看一小节（一个批次）。Batch Size就是这一小节包含的页数。
• Iteration（迭代） ：指模型处理一个批次数据，并完成一次参数更新的过程。如果训练集有1000个样本，Batch Size设为100，那么一个Epoch就需要1000/100=101000 / 100 = 101000/100=10次Iteration。

这三者的关系是：一个Epoch=总样本数/BatchSize个Iteration一个Epoch = 总样本数 / Batch Size 个Iteration一个Epoch=总样本数/BatchSize个Iteration。这种分批训练的方式不仅能有效利用计算资源，还能为梯度下降过程引入一定的随机性，有助于模型跳出局部最小值，提高泛化能力。

6.2 反向传播算法（BP算法）

反向传播算法是深度学习的"学习引擎"，它是一种高效计算损失函数对网络中每一个参数（权重和偏置）梯度的算法。如果说前向传播是模型"大胆猜测"的过程，那么反向传播就是模型"谦虚反思"的过程。它将最终预测的误差，像分配责任一样，精确地回溯到网络中的每一个参数，告诉每个参数"应该为这个错误承担多少责任"，从而为下一步的参数更新指明方向。

6.2.1 前向传播

前向传播是神经网络进行预测的"执行阶段"。它描述了数据从输入层开始，逐层通过隐藏层，最终到达输出层并产生结果的完整流程。

1. 过程解析：想象一个工厂的流水线。原始数据（如一张图片的像素值）是"原材料"，它被送入流水线的第一站（输入层）。每一站的工人（神经元）都对材料进行加工（加权求和并通过激活函数），然后将半成品传递给下一站。这个过程一层一层地进行，直到最后一站（输出层）产出最终产品（模型的预测结果，如分类概率或回归值）。
2. 核心目的：前向传播的核心目的是基于当前的模型参数，生成一个预测输出。这个输出是后续计算损失的基础。没有前向传播的"因"，就没有反向传播的"果"。

6.2.2 反向传播

反向传播是神经网络进行学习的"反思阶段"。它利用前向传播计算出的损失，从输出层开始，逐层向后计算梯度，并将误差信号传播回网络的每一层。

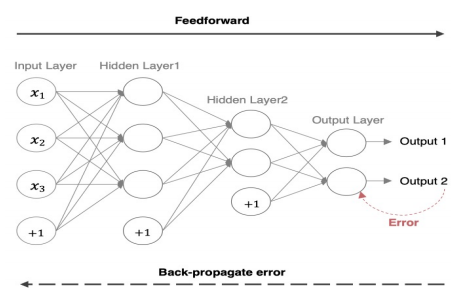
1. 核心机制 ：反向传播的数学精髓是微积分中的链式法则。它允许我们将一个复杂函数（整个网络的损失函数）的梯度，分解为一系列简单函数（每一层的计算）的梯度的乘积。这就像多米诺骨牌，要推倒第一块，需要通过中间所有骨牌的传递。
2. 过程解析：再次回到工厂的类比。假设最终产品（预测结果）被质检员判定为不合格（产生了损失）。为了改进，质检员需要从最后一道工序开始，反向追溯，找出每一道工序对最终不合格结果的"贡献度"。输出层对损失的贡献度最大，隐藏层次之，输入层再次之。反向传播算法就是这种"责任追溯"的数学实现，它精确地计算出每个权重参数对总损失的偏导数（即梯度）。
3. 与梯度下降的关系 ：需要明确的是，反向传播负责计算梯度，而梯度下降算法负责使用梯度来更新参数。二者是合作关系：反向传播是"军师"，负责提供精确的情报（梯度）；梯度下降是"将军"，根据情报下达行动指令（参数更新）。

6.2.3 数学示例

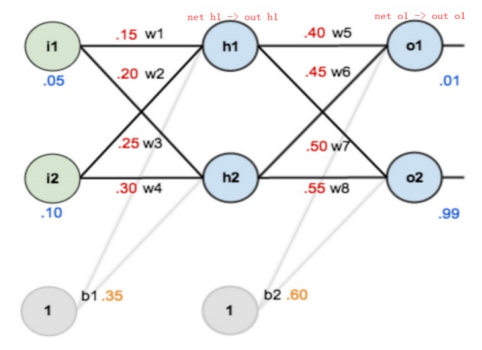
假设激活函数为Sigmoid：

1. 前向传播过程：
   • 输入到隐藏层 ：输入数据i1,i2i_1, i_2i1,i2与权重w1,w2w_1, w_2w1,w2及偏置b1b_1b1结合，通过加权求和得到neth1net_{h1}neth1，再经过Sigmoid激活函数得到隐藏层神经元的输出outh1out_{h1}outh1。这个过程模拟了神经元对输入信号的初步处理。
     • neth1=w1∗i1+w2∗i2+b1∗1net_{h1} = w_1 * i_1 + w_2 * i_2 + b_1 * 1neth1=w1∗i1+w2∗i2+b1∗1
     • neth1=0.15∗0.05+0.2∗0.1+0.35∗1=0.3775net_{h1} = 0.15 * 0.05 + 0.2 * 0.1 + 0.35 * 1 = 0.3775neth1=0.15∗0.05+0.2∗0.1+0.35∗1=0.3775
     • outh1=11+e−neth1=11+e−0.3775=0.593269992out_{h1} = \frac{1}{1 + e^{-net_{h1}}} = \frac{1}{1 + e^{-0.3775}} = 0.593269992outh1=1+e−neth11=1+e−0.37751=0.593269992
     • outh2=0.596884378out_{h2} = 0.596884378outh2=0.596884378
   • 隐藏层到输出层 ：隐藏层的输出outh1,outh2out_{h1}, out_{h2}outh1,outh2作为新的输入，与权重w5,w6w_5, w_6w5,w6及偏置b2b_2b2结合，再次通过加权求和与Sigmoid激活，得到最终的输出 outo1out_{o1}outo1。
     • neto1=w5∗outh1+w6∗outh2+b2∗1net_{o1} = w_5 * out_{h1} + w_6 * out_{h2} + b_2 * 1neto1=w5∗outh1+w6∗outh2+b2∗1
     • neto1=0.4∗0.593269992+0.45∗0.596884378+0.6∗1=1.105905967net_{o1} = 0.4 * 0.593269992 + 0.45 * 0.596884378 + 0.6 * 1 = 1.105905967neto1=0.4∗0.593269992+0.45∗0.596884378+0.6∗1=1.105905967
     • outo1=11+e−neto1=11+e−1.105905967=0.75136507out_{o1} = \frac{1}{1 + e^{-net_{o1}}} = \frac{1}{1 + e^{-1.105905967}} = 0.75136507outo1=1+e−neto11=1+e−1.1059059671=0.75136507
     • outo2=0.772928465out_{o2} = 0.772928465outo2=0.772928465
   • 计算总损失 ：将模型的输出outo1out_{o1}outo1与真实标签targeto1target_{o1}targeto1比较，使用均方误差公式计算出总损失EtotalE_{total}Etotal。至此，前向传播完成，我们得到了一个具体的损失值。
     • Etotal=∑12(target−output)2E_{total} = \sum \frac{1}{2} (target - output)^2Etotal=∑21(target−output)2
     • Etotal=Eo1+Eo2=0.274811083+0.023560026=0.298371109E_{total} = E_{o1} + E_{o2} = 0.274811083 + 0.023560026 = 0.298371109Etotal=Eo1+Eo2=0.274811083+0.023560026=0.298371109
2. 反向传播过程：
   • 计算输出层权重梯度 （以w5w_5w5为例）：这是最简单的一步反向传播。我们想知道w5w_5w5的微小变化对总损失EtotalE_{total}Etotal的影响。根据链式法则，这个影响可以分解为：w5w_5w5的变化→影响neto1net_{o1}neto1→影响outo1out_{o1}outo1→影响EtotalE_{total}Etotal。因此，梯度∂Etotal∂w5\frac{\partial E_{total}}{\partial w_5}∂w5∂Etotal就等于这三个环节偏导数的乘积。
     
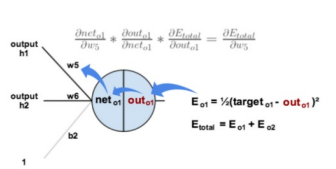
     • Etotal=12(targeto1−outo1)2+12(targeto2−outo2)2E_{total} = \frac{1}{2}(target_{o1} - out_{o1})^2 + \frac{1}{2}(target_{o2} - out_{o2})^2Etotal=21(targeto1−outo1)2+21(targeto2−outo2)2
     • ∂Etotal∂outo1=2×12(targeto1−outo1)2−1−1×0=−(targeto1−outo1)=−(0.01−0.75136507)=0.74136507\frac{\partial E_{total}}{\partial out_{o1}} = 2 \times \frac{1}{2}(target_{o1} - out_{o1})^{2-1} - 1 \times 0 = -(target_{o1} - out_{o1}) = -(0.01 - 0.75136507) = 0.74136507∂outo1∂Etotal=2×21(targeto1−outo1)2−1−1×0=−(targeto1−outo1)=−(0.01−0.75136507)=0.74136507
     • outo1=11+e−neto1out_{o1} = \frac{1}{1 + e^{-net_{o1}}}outo1=1+e−neto11
     • ∂outo1∂neto1=outo1(1−outo1)=0.75136507(1−0.75136507)=0.186815602\frac{\partial out_{o1}}{\partial net_{o1}} = out_{o1}(1 - out_{o1}) = 0.75136507(1 - 0.75136507) = 0.186815602∂neto1∂outo1=outo1(1−outo1)=0.75136507(1−0.75136507)=0.186815602
     • neto1=w5⋅outh1+w6⋅outh2+b2⋅1net_{o1} = w_5 \cdot out_{h1} + w_6 \cdot out_{h2} + b_2 \cdot 1neto1=w5⋅outh1+w6⋅outh2+b2⋅1
     • ∂Etotal∂w5=∂Etotal∂outo1⋅∂outo1∂neto1⋅∂neto1∂w5=0.74136507×0.186815602×0.593269992=0.082167041\frac{\partial E_{total}}{\partial w_5} = \frac{\partial E_{total}}{\partial out_{o1}} \cdot \frac{\partial out_{o1}}{\partial net_{o1}} \cdot \frac{\partial net_{o1}}{\partial w_5} = 0.74136507 \times 0.186815602 \times 0.593269992 = 0.082167041∂w5∂Etotal=∂outo1∂Etotal⋅∂neto1∂outo1⋅∂w5∂neto1=0.74136507×0.186815602×0.593269992=0.082167041
   • 参数更新 ：一旦计算出所有参数的梯度，就可以使用梯度下降公式Wnew=Wold−η⋅gradientW^{new} = W^{old} - \eta \cdot \text{gradient}Wnew=Wold−η⋅gradient来更新权重。
     
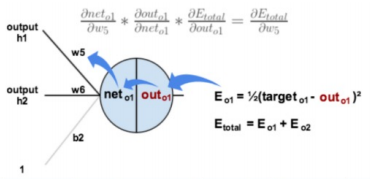
     • ∂Etotal∂w5=−(targeto1−outo1)⋅outo1(1−outo1)⋅outh1\frac{\partial E_{total}}{\partial w_5} = -(target_{o1} - out_{o1}) \cdot out_{o1}(1 - out_{o1}) \cdot out_{h1}∂w5∂Etotal=−(targeto1−outo1)⋅outo1(1−outo1)⋅outh1
     • w5+=w5−η⋅∂Etotal∂w5=0.4−0.5⋅0.082167041=0.35891648w_5^+ = w_5 - \eta \cdot \frac{\partial E_{total}}{\partial w_5} = 0.4 - 0.5 \cdot 0.082167041 = 0.35891648w5+=w5−η⋅∂w5∂Etotal=0.4−0.5⋅0.082167041=0.35891648
   • 计算隐藏层权重梯度 （以w1w_1w1为例）：这一步更复杂，因为w1w_1w1的变化会同时影响两个输出神经元outo1out_{o1}outo1和outo2out_{o2}outo2，进而影响总损失。因此，计算w1w_1w1的梯度时，需要将来自outo1out_{o1}outo1和outo2out_{o2}outo2的两条路径的梯度相加 。这完美体现了误差信号在网络中的"汇聚"与"传播"。
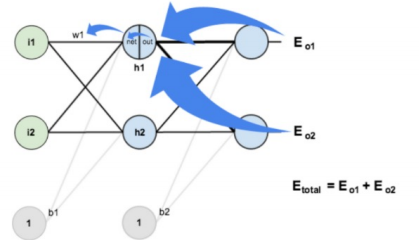
     • ∂Etotal∂w1=(∑o∂Etotal∂outo⋅∂outo∂neto⋅∂neto∂outh1⋅∂outh1∂neth1)⋅∂neth1∂w1\frac{\partial E_{total}}{\partial w_1} = \left( \sum_o \frac{\partial E_{total}}{\partial out_o} \cdot \frac{\partial out_o}{\partial net_o} \cdot \frac{\partial net_o}{\partial out_{h1}} \cdot \frac{\partial out_{h1}}{\partial net_{h1}} \right) \cdot \frac{\partial net_{h1}}{\partial w_1}∂w1∂Etotal=(∑o∂outo∂Etotal⋅∂neto∂outo⋅∂outh1∂neto⋅∂neth1∂outh1)⋅∂w1∂neth1
     • w1+=w1−η⋅∂Etotal∂w1=0.15−0.5×0.000438568=0.149780716w_1^+ = w_1 - \eta \cdot \frac{\partial E_{total}}{\partial w_1} = 0.15 - 0.5 \times 0.000438568 = 0.149780716w1+=w1−η⋅∂w1∂Etotal=0.15−0.5×0.000438568=0.149780716

6.3 梯度下降的优化算法

标准的梯度下降算法虽然原理简单，但在实际应用中却常常面临"心有余而力不足"的困境。它像一个只会埋头走路的人，容易在平坦的平地上停滞不前，也可能被困在局部的小坑里无法自拔，或者在狭窄的山谷中来回震荡。为了克服这些缺陷，一系列更为智能的优化算法应运而生。它们不再是简单地"跟着感觉走"，而是通过引入"记忆"、"惯性"和"自适应"等机制，让模型的学习过程变得更快速、更稳定、更智能。

6.3.1 梯度下降的问题

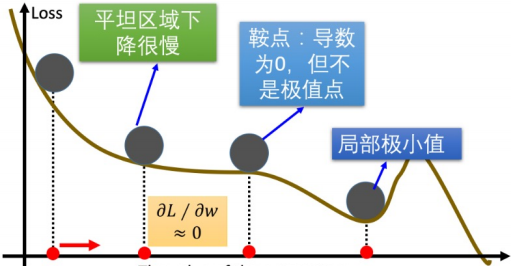
这是所有优化算法需要面对的"三大挑战"，也是催生它们的根本原因：

• 平缓区域（学习缓慢）：当损失函数曲面非常平坦时，梯度值会变得极小。这导致参数更新的步长微乎其微，模型仿佛在原地踏步，训练过程极其缓慢。
• 鞍点（陷入停滞）：在高维空间中，存在一种特殊的点，它在一个方向上是局部最小值，但在其他方向上是局部最大值，形似马鞍。在鞍点处，梯度为零，标准梯度下降会完全停止，无法找到更优的解。
• 局部最小值（非全局最优）：损失函数通常有多个"山谷"，模型可能会陷入一个较浅的局部最小值（小山谷），而错失了那个更深的、真正的全局最小值（最深的山谷）。

6.3.2 指数加权平均算法

指数加权平均算法是现代深度学习优化器（如动量法、Adam等）的基石，它并非一个独立的优化算法，而是一种核心的数学工具。其核心思想是：在计算一系列数值的平均值时，赋予不同时间点的数据以不同的权重。具体而言，越近期的数据，对当前决策的影响越大；越久远的数据，影响越小，且这种影响是按指数级衰减的。它就像一个拥有"短期记忆"的系统，能够平滑掉数据中的短期噪声，从而捕捉到更本质的长期趋势。

（1）定义

从定义上看，指数加权平均是一种特殊的加权平均。与算术平均中每个数据点权重相同不同，EMA的权重分配具有明确的时间偏向性。它认为，最新的信息最能反映当前状况，因此应给予最高的权重；而历史信息虽然仍有参考价值，但其重要性会随着时间的推移而迅速降低。这种厚今薄古的策略，使得它在处理时间序列数据或充满噪声的信号时，能够有效地提取出核心趋势，过滤掉随机波动带来的干扰。

（2）数学原理

EMA的递归公式是算法的精髓，它以极其高效的方式实现了上述思想：
St={Y1,t=0β⋅St−1+(1−β)⋅Yt,t>0 S_t = \begin{cases} Y_1, & t = 0 \\ \beta \cdot S_{t-1} + (1 - \beta) \cdot Y_t, & t > 0 \end{cases} St={Y1,β⋅St−1+(1−β)⋅Yt,t=0t>0

这个公式可以通俗地理解为：新的平均值 = 过去的平均值 × 记忆保留程度 + 当前值 × 当前重视程度。

• St−1S_{t-1}St−1：代表了"过去"的累积记忆，即上一时刻的指数加权平均值。
• YtY_tYt：代表了"现在"的新信息，即当前时刻的数值。
• βββ：是一个介于0和1之间的关键超参数，被称为衰减率或平滑因子。它控制着记忆的长度：
  • 当β越大（如0.9），意味着更重视过去的历史数据，记忆更长，计算出的曲线越平滑，对短期噪声不敏感。
  • 当β越小（如0.5），意味着更关注当前的数据点，记忆越短，曲线会紧跟数据的最新变化，反应更灵敏。
• (1−β)(1-β)(1−β)：是赋予当前值YtY_tYt的权重。

（3）代码示例

import torch
import matplotlib.pyplot as plt

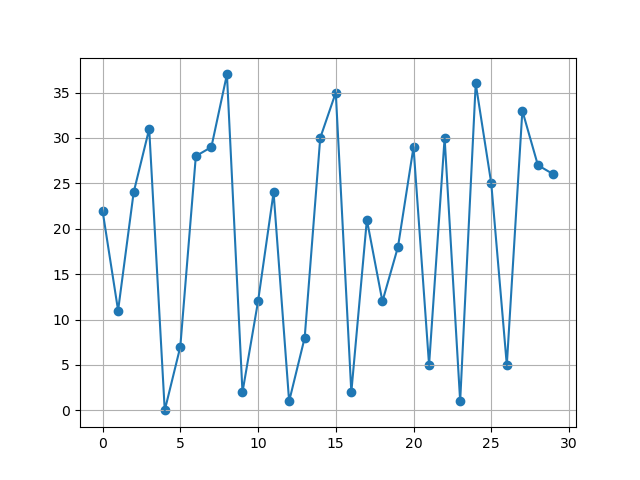
temperatures = torch.randint(0, 40, [30])
print(temperatures)
days = torch.arange(0, 30, 1)
plt.plot(days, temperatures)
plt.scatter(days, temperatures)
plt.grid()
plt.show()

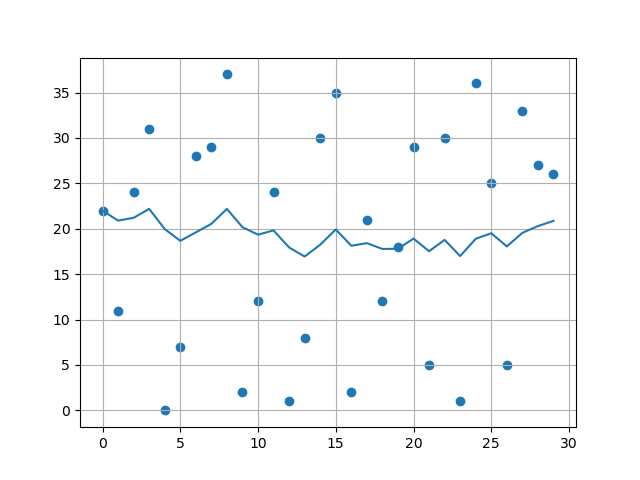
t_avg = []
beta = 0.9
for i, temp in enumerate(temperatures):
    if i == 0:
        t_avg.append(temp)
        continue

    t2 = beta*t_avg[i-1] + (1-beta)*temp
    t_avg.append(t2)

plt.plot(days, t_avg)
plt.scatter(days, temperatures)
plt.grid()
plt.show()

• 代码输出：
  
  

6.3.3 动量算法

动量算法是对标准梯度下降算法的一项关键改进，它巧妙地借鉴了物理学中的"惯性"概念。想象一下，一个球从山坡上滚下，它不仅会根据当前坡度（梯度）调整方向，还会因为自身的惯性而保持前进的趋势。动量算法正是为梯度下降过程引入了这种"惯性"，使得参数更新不再仅仅依赖于当前批次的梯度，而是综合考虑了历史梯度的趋势。

（1）数学原理

动量算法的数学核心，正是对梯度 进行指数加权平均：
Dt=β⋅St−1+(1−β)⋅Wt Dt = \beta \cdot S_{t-1} + (1 - \beta) \cdot Wt Dt=β⋅St−1+(1−β)⋅Wt

这个公式与6.3.2中的指数加权平均算法在形式上完全一致，但其应用对象发生了根本变化：

• WtWtWt：不再是任意数值，而是当前时刻计算出的原始梯度。
• St−1S_{t-1}St−1：是上一时刻更新后的动量值（即平滑后的梯度）。
• DtDtDt：是当前时刻最终用于更新参数的动量值（即平滑后的梯度）。
• βββ：是动量系数，通常设置为0.9左右，它决定了历史梯度信息的保留程度。

因此，动量算法的本质是：用过去梯度的指数加权平均，来指导当前参数的更新方向。它不再盲目地跟随当前可能充满噪声的梯度，而是沿着一个经过平滑的、更可信的方向前进。

（2）解决问题

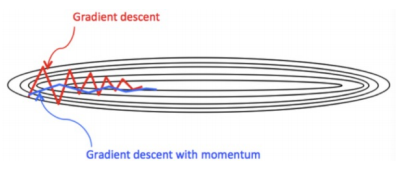
动量算法的"惯性"特性，使其能够有效解决标准梯度下降面临的两大难题：

• 冲出鞍点：当优化过程陷入鞍点（当前梯度为零）时，标准梯度下降会完全停滞。但动量算法由于保留了历史梯度的"冲力"，它有很大概率会凭借惯性直接滑过这个平坦区域，继续寻找更优的解。
• 抑制震荡，加速收敛：在使用mini-batch训练时，每个批次的梯度都可能存在噪声，导致更新路径在狭窄的山谷中来回震荡，收敛缓慢。动量算法通过平滑梯度变化，为优化过程提供了一个更稳定、更一致的前进方向，就像给滚动的球增加了质量，使其不易被微小的地形变化所干扰，从而能够更快地抵达谷底。

（3）代码示例

import torch
import torch.nn as nn

# （1）原始
w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)
loss = ((w**2) * 0.5).sum()

optimizer = torch.optim.SGD([w], lr=0.01)

optimizer.zero_grad()
loss.backward()
optimizer.step()
print(w.grad)
print(w.detach())

loss = ((w**2) * 0.5).sum()
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(w.grad)
print(w.detach())

print('--'*50)
# （2）动量法
w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)
loss = ((w**2) * 0.5).sum()

optimizer = torch.optim.SGD([w], lr=0.01, momentum=0.9)

optimizer.zero_grad()
loss.backward()
optimizer.step()
print(w.grad)
print(w.detach())

loss = ((w**2) * 0.5).sum()
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(w.grad)
print(w.detach())

• 代码输出：

  tensor([1.])
  tensor([0.9900])
  tensor([0.9900])
  tensor([0.9801])

  tensor([1.])
  tensor([0.9900])
  tensor([0.9900])
  tensor([0.9711])

6.3.4 adagrad算法

Adagrad（Adaptive Gradient Algorithm）算法是深度学习优化领域中一次里程碑式的创新，它开创了"自适应学习率"的先河。其核心思想是：为每个参数设置一个独立的学习率，并根据该参数在历史训练中的表现动态调整。这就像为模型中的每个参数都配备了一位"个性化教练"，对于频繁更新、梯度较大的参数，教练会建议它放慢脚步，谨慎前行；而对于更新稀疏、梯度较小的参数，教练则会鼓励它迈开大步，加速学习。

（1）数学原理

Adagrad的数学公式清晰地体现了其自适应机制：

• 参数更新公式 ：θ=θ−αs+σ⋅g\theta = \theta - \frac{\alpha}{\sqrt{s + \sigma}} \cdot gθ=θ−s+σ α⋅g
• 有效学习率公式 ：αeffective=αs+σ\alpha_{effective} = \frac{\alpha}{\sqrt{s + \sigma}}αeffective=s+σ α

（2）计算过程

Adagrad的计算过程严谨地执行了上述数学思想，其核心步骤如下：

1. 初始化 ：设定一个全局初始学习率α\alphaα，初始化所有模型参数θ\thetaθ，并设置一个非常小的常数σ\sigmaσ（如1e-6）以防止分母为零。最关键的是，为每个参数初始化一个梯度平方累积变量sss，并将其置为0。
2. 迭代更新 ：在每次迭代中：
   • 从训练集中采样一个小批量数据，计算当前批次下所有参数的梯度ggg。
   • 关键步骤 ：对每个参数，将其当前梯度的平方g⊙gg \odot gg⊙g累加到其对应的累积变量sss上，即s=s+g⊙gs = s + g \odot gs=s+g⊙g。
   • 使用更新后的sss计算该参数的有效学习率，并更新参数本身。

（3）主要缺点

Adagrad最大的优点------自适应，也导致了其最致命的缺点：学习率的单调、无限制衰减。

• 问题根源 ：由于累积变量sss是一个只增不减的值（它一直在累加梯度的平方），随着训练的进行，sss会变得越来越大。
• 后果 ：当sss增大到一定程度后，分母s+σ\sqrt{s + \sigma}s+σ 会变得极其巨大，导致有效学习率α/s+σ\alpha / \sqrt{s + \sigma}α/s+σ 趋近于零。
• 影响：在训练后期，学习率会变得过小，使得参数更新的步长微乎其微，模型几乎停止学习。这就像一辆自动减速的汽车，最终会慢到无法到达目的地，即使离终点已经很近。这使得Adagrad在很多需要长期训练的深度学习任务中表现不佳。

（4）代码示例

import torch

w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)
loss = ((w**2) * 0.5).sum()

optimizer = torch.optim.Adagrad([w], lr=0.01)

optimizer.zero_grad()
loss.backward()
optimizer.step()
print(w.grad)
print(w.detach())

loss = ((w**2) * 0.5).sum()
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(w.grad)
print(w.detach())

• 代码输出：

  tensor([1.])
  tensor([0.9900])
  tensor([0.9900])
  tensor([0.9830])

6.3.5 rmsprop算法

RMSprop（Root Mean Square Propagation）算法是对Adagrad算法的一次关键性改进，它精准地修复了Adagrad最致命的缺陷。如果说Adagrad是一个记忆力过强、从不遗忘的"学霸"，那么RMSprop就是一个懂得"遗忘"、只关注近期重点的"聪明学生"。它通过引入一种更智能的历史信息处理方式，确保模型在漫长的训练后期依然能够保持高效的学习能力。

（1）数学原理

从数学公式上看，RMSprop与Adagrad的参数更新形式完全相同，这常常引起初学者的困惑：

• 参数更新公式 ：θ=θ−αs+σ⋅g\theta = \theta - \frac{\alpha}{\sqrt{s + \sigma}} \cdot gθ=θ−s+σ α⋅g
• 有效学习率公式 ：αeffective=αs+σ\alpha_{effective} = \frac{\alpha}{\sqrt{s + \sigma}}αeffective=s+σ α

（2）计算过程

1. 初始化 ：与Adagrad相同，初始化学习率α\alphaα、参数θ\thetaθ、小常数σ\sigmaσ和梯度累积变量sss。
2. 采样与计算梯度 ：从训练集中采样一个小批量，计算当前梯度ggg。
3. 更新累积变量 ：这是与Adagrad最本质的区别。RMSprop使用指数移动平均 来更新sss：
   s=β⋅s+(1−β)g⊙g s = \beta \cdot s + (1 - \beta) g \odot g s=β⋅s+(1−β)g⊙g
   这个公式意味着，新的sss值是旧sss值与当前梯度平方g⊙gg \odot gg⊙g的加权平均。衰减率β\betaβ（通常设为0.9）控制着历史信息的保留程度。这相当于给算法装上了一个"遗忘开关"，使得过于久远的梯度信息会逐渐被"冲淡"，只有近期的梯度信息对当前决策有较大影响。
4. 参数更新 ：使用更新后的sss计算有效学习率并更新参数。

（3）与adagrad算法的区别

RMSprop与Adagrad的根本区别在于用指数移动加权平均替换了历史梯度的平方和。

• Adagrad的问题 ：累加所有历史梯度平方，导致sss单调递增，最终使学习率趋近于零，训练提前终止。
• RMSprop的解决方案 ：通过指数移动平均，sss的值会趋于一个稳定范围，而不会无限增长。这意味着分母s+σ\sqrt{s + \sigma}s+σ 也会稳定下来，从而保证了在训练后期，学习率依然能保持在一个合理的水平，让模型有能力继续学习和优化。这完美地解决了Adagrad学习率过早、过量降低的问题。

（4）代码示例

import torch

w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)
loss = ((w**2) * 0.5).sum()

optimizer = torch.optim.RMSprop([w], lr=0.01, alpha=0.9)

optimizer.zero_grad()
loss.backward()
optimizer.step()
print(w.grad)
print(w.detach())

loss = ((w**2) * 0.5).sum()
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(w.grad)
print(w.detach())

• 代码输出：

  tensor([1.])
  tensor([0.9684])
  tensor([0.9684])
  tensor([0.9458])

6.3.6 adam算法

Adam（Adaptive Moment Estimation，自适应矩估计）算法是深度学习优化领域当之无愧的"王者"，它凭借其出色的综合性能，成为了目前最流行、应用最广泛的优化算法。Adam并非凭空创造，而是一位集大成者，它巧妙地融合了动量法和RMSProp两种优秀算法的核心思想，取其精华，形成了一个既快速又稳定的强大优化器。其名称"自适应矩估计"精准地概括了其工作原理：自适应地估计并利用梯度的一阶矩（均值）和二阶矩（方差）。

（1）核心机制

Adam算法的精髓在于它同时维护两个独立的累积变量，分别追踪梯度信息的不同方面：

• 动量项（一阶矩估计） ：这部分完全借鉴了Momentum算法的思想。它计算梯度ggg的指数移动平均（EMA），即EMA(g)\text{EMA}(g)EMA(g)。这相当于为优化过程注入了"惯性"，能够平滑掉单批次梯度中的随机噪声，保持一个稳定的前进方向，从而有效穿越鞍点并抑制震荡。
• 方差项（二阶矩估计） ：这部分则借鉴了RMSProp算法的思想。它计算梯度平方g2g^2g2的指数移动平均（EMA），即EMA(g2)\text{EMA}(g^2)EMA(g2)。这相当于为每个参数量身定制一个动态的学习率，使得梯度较大的参数自动减小步长，而梯度较小的参数则保持较大的步长。

通过同时维护这两个"记忆"，Adam在更新参数时，既能知道"该往哪个方向走（动量）"，又清楚"该走多远（自适应学习率）"，实现了方向与步长的双重优化。

（2）修正梯度

在每次参数更新时，Adam并非直接使用当前计算出的原始梯度ggg，而是使用经过指数加权平均平滑后的梯度。这个平滑后的梯度，融合了历史梯度的趋势，使得更新方向更加可靠和稳定。这就像一个经验丰富的航海家，他不仅看当前的风向（当前梯度），更会结合过去一段时间的风向趋势（历史梯度EMA）来调整船舵，从而更平稳、更快速地驶向目的地。

（3）修正学习率

在确定了更新方向后，Adam会利用梯度平方的指数移动平均值来调整每个参数的学习率。具体来说，它会用全局学习率除以一个与梯度平方的EMA相关的项。这意味着，对于那些在训练中一直很"活跃"、梯度值很大的参数，其有效学习率会被自动调低，防止其步子迈得太大而"跑过头"；而对于那些"沉寂"已久、梯度值很小的参数，其有效学习率则会相对较高，鼓励它们进行更大幅度的更新。这种精细化的调整，使得整个训练过程异常高效和鲁棒。

6.4 学习率优化算法

6.4.1 等间隔衰减

（1）函数定义

lr_scheduler.StepLR(optimizer, step_size, gamma=0.1)
# 功能：等间隔-调整学习率
# 参数：
# step_size：调整间隔数=50
# gamma：调整系数=0.5
# 调整方式：lr = lr * gamma

（2）代码示例

# 参数初始化
lr = 0.1
iter = 100
epoches = 200

# 网络数据初始化
x = torch.tensor([1.0])
w = torch.tensor([1.0], requires_grad=True)
y = torch.tensor([1.0])

# 优化器
optimizer = torch.optim.SGD([w], lr=lr, momentum=0.9)

# 学习率策略
LR_scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=20, gamma=0.8)

# 遍历轮次
epoches_list = []
lr_list = []
for epoch in range(epoches):
    lr_list.append(LR_scheduler.get_last_lr())
    epoches_list.append(epoch)

    # 遍历batch
    for i in range(iter):

        # 计算损失
        loss = ((w*x - y)**2) * 0.5

        # 更新参数
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

    # 更新lr
    LR_scheduler.step()

# 绘制结果
plt.plot(epoches_list, lr_list)
plt.title('等间隔')
plt.grid()
plt.show()

• 代码输出：
  

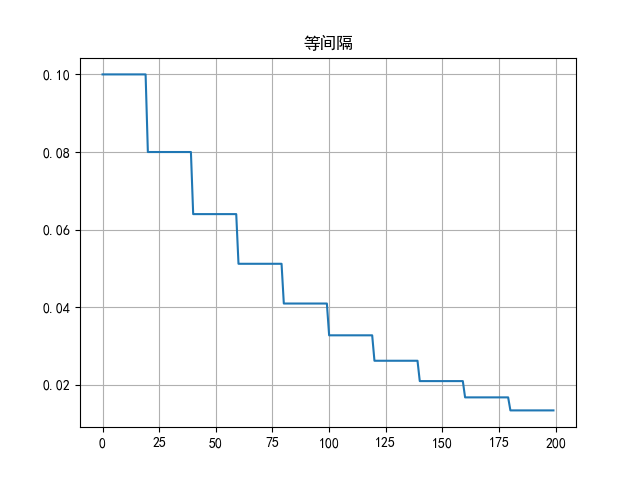
6.4.2 指定间隔衰减

（1）函数定义

lr_scheduler.MultiStepLR(optimizer, milestones, gamma=0.1)
# 功能：指定间隔-调整学习率
# 主要参数：
# milestones：设定调整轮次:[50, 125, 160]
# gamma：调整系数
# 调整方式：lr = lr * gamma

（2）代码示例

# 参数初始化
lr = 0.1
iter = 100
epoches = 200

# 网络数据初始化
x = torch.tensor([1.0])
w = torch.tensor([1.0], requires_grad=True)
y = torch.tensor([1.0])

# 优化器
optimizer = torch.optim.SGD([w], lr=lr, momentum=0.9)

# 学习率策略
LR_scheduler = torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones=[10, 20, 40, 60, 90, 120, 160], gamma=0.8)

# 遍历轮次
epoches_list = []
lr_list = []
for epoch in range(epoches):
    lr_list.append(LR_scheduler.get_last_lr())
    epoches_list.append(epoch)

    # 遍历batch
    for i in range(iter):

        # 计算损失
        loss = ((w*x - y)**2) * 0.5

        # 更新参数
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

    # 更新lr
    LR_scheduler.step()

# 绘制结果
plt.plot(epoches_list, lr_list)
plt.title('指定间隔')
plt.grid()
plt.show()

• 代码输出：
  

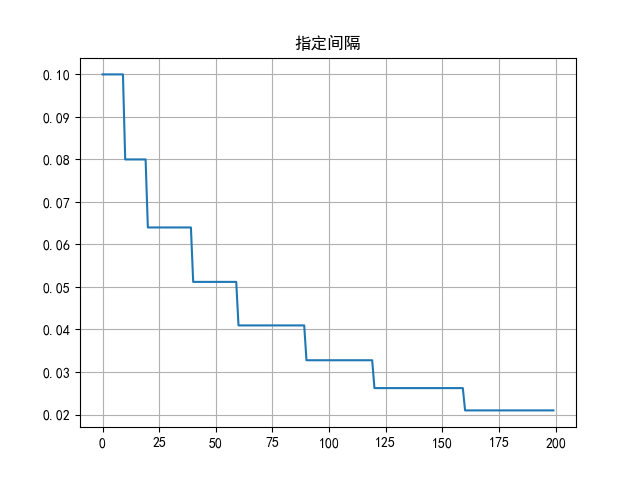
6.4.3 指数衰减

（1）函数定义

lr_scheduler.ExponentialLR(optimizer, gamma)
# 功能：按指数衰减-调整学习率
# 主要参数：
# gamma：指数的底
# 调整方式
# lr= lr∗ gamma^epoch

（2）代码示例

# 参数初始化
lr = 0.1
iter = 100
epoches = 200

# 网络数据初始化
x = torch.tensor([1.0])
w = torch.tensor([1.0], requires_grad=True)
y = torch.tensor([1.0])

# 优化器
optimizer = torch.optim.SGD([w], lr=lr, momentum=0.9)

# 学习率策略
LR_scheduler = torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma=0.8)

# 遍历轮次
epoches_list = []
lr_list = []
for epoch in range(epoches):
    lr_list.append(LR_scheduler.get_last_lr())
    epoches_list.append(epoch)

    # 遍历batch
    for i in range(iter):

        # 计算损失
        loss = ((w*x - y)**2) * 0.5

        # 更新参数
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

    # 更新lr
    LR_scheduler.step()

# 绘制结果
plt.plot(epoches_list, lr_list)
plt.title('指数')
plt.grid()
plt.show()

• 代码输出：
  

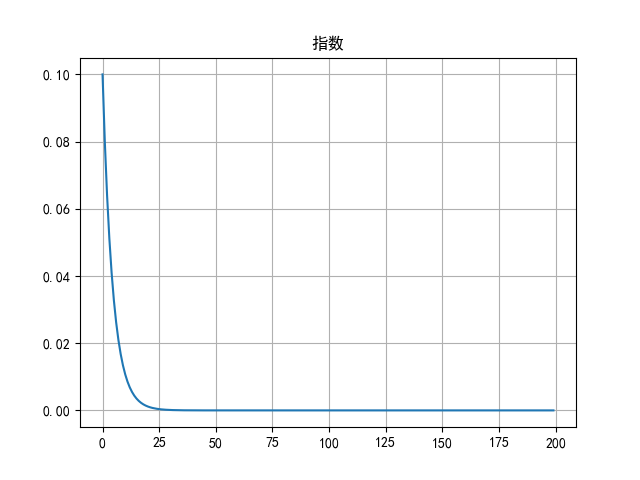
七、正则化

正则化是深度学习中防止模型"死记硬背"并提升其"举一反三"能力的关键技术集合。它的核心目标是增强模型的泛化能力，即模型在从未见过的新数据上的表现。一个没有正则化的模型，可能会在训练数据上表现得完美无瑕，但在实际应用中却一塌糊涂，这种现象我们称之为过拟合。正则化通过在训练过程中引入一些"约束"或"噪声"，迫使模型学习数据中更本质、更普适的规律，而不是去记忆训练数据中的噪声和特例。

7.1 正则化的定义

从本质上讲，正则化是一类用于减小测试误差的策略总和。在机器学习中，我们追求的并非是在训练集上达到最低的训练误差，而是在未知数据上取得最低的测试误差。正则化正是为了弥合这两者之间的鸿沟而生。它通过在损失函数中添加一个惩罚项（如L1/L2正则化）或改变训练过程本身（如Dropout），来限制模型的复杂度，从而避免模型变得过于"聪明"以至于只学会了背诵答案。

7.2 正则化的作用

正则化的主要作用是对抗过拟合。神经网络拥有海量的参数和强大的非线性拟合能力，这使其像一个拥有超强记忆力的学生，不仅能学会知识要点，还能把练习册上的每一个印刷错误都背下来。这种"过度学习"导致模型无法泛化到新的、略有不同的数据上。正则化就像是给这个学生施加的一种"纪律"，它不允许模型过度依赖任何一个或某几个参数，鼓励它构建一个更简洁、更鲁棒的模型，从而抓住数据的核心模式，忽略无关的噪声。

7.3 dropout算法

7.3.1 核心功能

Dropout的核心功能是防止神经网络在训练过程中发生过拟合。它通过一种"以退为进"的策略实现这一目标：

• 在训练阶段 ：
  1. 随机失活 ：对于网络的每一层，Dropout会以一个预设的概率p（例如0.5）随机选择一部分神经元，使其在本次前向传播和反向传播中完全"失活"。这意味着这些神经元的输出将被置为0，并且它们也不会参与参数的更新。
  2. 缩放补偿 ：为了保持网络输出的期望值不变，未被丢弃的神经元的输出需要按比例放大。具体来说，它们的输出会乘以一个缩放因子1 / (1-p)。这种做法被称为"Inverted Dropout"，是现代深度学习框架中的标准实现。
  3. 训练子网络：从另一个角度看，每一次迭代，Dropout实际上都是在训练一个"瘦身"后的子网络。由于每次丢弃的神经元都是随机的，所以在整个训练过程中，网络相当于在训练指数级数量的不同子网络。
• 在测试/推理阶段 ：
  1. 关闭Dropout：在模型进行预测时，Dropout功能会被完全关闭。所有神经元都参与计算，以确保模型利用其全部能力做出最准确的判断。
  2. 权重调整 ：由于在训练时已经对输出进行了1/(1-p)的缩放，因此在测试时无需再对权重进行额外调整，模型可以直接使用完整的网络结构进行推理。

7.3.2 核心机制

Dropout的有效性源于其独特的机制，它从根本上改变了网络的学习方式：

1. 打破神经元间的共适应：在没有Dropout的网络中，一些神经元之间可能会发展出复杂的协同关系，形成"小团体"。这种共适应使得模型过度依赖这些特定的神经元组合，从而降低了泛化能力。Dropout通过随机丢弃神经元，强制性地打破了这种共适应，使得任何神经元都不能过分依赖其他少数几个神经元的存在。
2. 迫使学习独立且鲁棒的特征：由于任何一个神经元都有可能在下一次迭代中被"干掉"，网络被迫学习到更加独立和有用的特征。它不能只依赖某一个"超级特征检测器"，而是要构建一个由多个"还不错"的特征检测器组成的团队，这样即使失去几个成员，整个团队依然能正常工作。
3. 模型集成效果：Dropout可以被看作是一种高效、廉价的模型集成方法。最终的模型，实际上是训练过程中所有"子网络"的加权平均。集成学习通常能显著提高模型的稳定性和泛化能力，而Dropout以一种非常巧妙的方式实现了这一点。

7.3.3 代码示例

import torch
import torch.nn as nn

input = torch.randn([1, 4])
layer = nn.Linear(in_features=4, out_features=5)
output = layer(input)
print(f"没有正则化的输出为：{output}")

dropout = nn.Dropout(p=0.75)
output = dropout(output)
print(f"正则化后的输出为：{output}")

• 代码输出：

  没有正则化的输出为：tensor([[-0.2369, 0.7376, -0.6863, 0.3419, 0.1905]],
  grad_fn=<AddmmBackward0>)
  正则化后的输出为：tensor([[-0.9477, 0.0000, -2.7452, 1.3675, 0.7621]], grad_fn=<MulBackward0>)

7.4 批量归一化（BN层）

7.4.1 核心功能

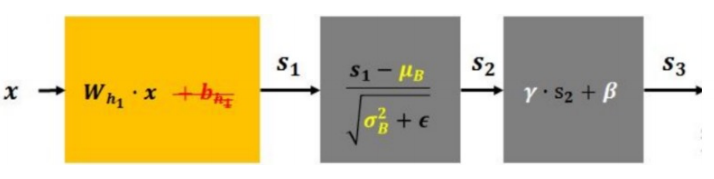
BN层的工作流程可以精炼地分为两个步骤，它像一个智能的"数据调理师"，安插在网络的各个隐藏层之间：

1. 第一步：标准化
   • 操作 ：对于进入该层的一个小批量的数据，BN层会计算这批数据的均值E(x)E(x)E(x)和方差Var(x)\text{Var}(x)Var(x)。然后，它利用这两个统计量，将该批量中的每一个数据点xxx进行标准化，使其变换为均值为0、方差为1的标准正态分布。
   • 目的 ：这一步旨在解决所谓的内部协变量偏移问题。简单来说，在深度网络中，每一层的输入都是前一层的输出。在训练过程中，前一层参数的更新会导致其后一层的输入分布不断变化，这使得后一层需要不断地去适应新的数据分布，训练过程因此变得非常缓慢且不稳定。BN层通过在每一层前都进行标准化，强制将每一层的输入分布"拉回"到一个稳定的状态，从而极大地加速了训练收敛。
2. 第二步：重构（缩放与平移）
   • 操作 ：仅仅将数据标准化是不够的，因为这可能会限制网络学习非线性特征的能力。因此，BN层引入了两个可学习的参数：缩放因子λ\lambdaλ和平移因子β\betaβ。标准化后的数据会先乘以λ\lambdaλ，再加上β\betaβ。
   • 目的 ：这赋予了网络灵活性。网络可以通过学习，自主决定在标准化之后，是否需要以及如何改变数据的分布。如果网络认为当前的最优分布就是标准正态分布，它可以学习到λ=1,β=0\lambda=1, \beta=0λ=1,β=0。如果它认为一个不同的均值和方差更有利于特征提取，它就会学习到相应的λ\lambdaλ和β\betaβ值。这保证了在享受标准化带来的训练稳定性的同时，不损失网络的表示能力。

7.4.2 数学原理

BN层的操作可以用一个优雅的公式来概括：
f(x)=λ⋅x−E(x)Var(x)+ε+β f(x) = \lambda \cdot \frac{x - E(x)}{\sqrt{\text{Var}(x) + \varepsilon}} + \beta f(x)=λ⋅Var(x)+ε x−E(x)+β

让我们来拆解这个公式：

• x−E(x)Var(x)+ε\frac{x - E(x)}{\sqrt{\text{Var}(x) + \varepsilon}}Var(x)+ε x−E(x)：这是标准化的核心部分。
  • x−E(x)x - E(x)x−E(x)：将数据xxx减去批量均值E(x)E(x)E(x)，实现数据中心化。
  • Var(x)+ε\sqrt{\text{Var}(x) + \varepsilon}Var(x)+ε ：计算批量标准差。ε\varepsilonε是一个极小的常数（如1e-5），用于防止分母为零，保证数值计算的稳定性。
• λ⋅(...)+β\lambda \cdot (\text{...}) + \betaλ⋅(...)+β：这是重构部分。
  • λ\lambdaλ：可学习的缩放参数。
  • β\betaβ：可学习的平移参数。

7.4.3 核心优势

BN层之所以成为现代深度学习架构的标配，是因为它一举多得：

1. 允许更大的学习率：由于BN层稳定了各层的输入分布，我们可以使用更大的学习率来加速训练，而不必担心梯度爆炸或消失。
2. 降低对权重初始化的依赖：BN层减弱了网络对初始权重值的敏感度，使得权重初始化变得不再那么关键。
3. 轻微的正则化效果：由于每个批次的均值和方差都是基于该批次数据计算得出的，这为网络的激活值引入了微小的随机噪声。这种噪声在一定程度上起到了正则化的作用，有助于抑制过拟合，效果类似于Dropout。
4. 缓解梯度消失问题：通过将activations保持在更健康的数值范围内，BN层有助于缓解深度网络中的梯度消失问题。

总而言之，批量归一化通过其先标准化，再重构的机制，为深度网络的训练过程提供了前所未有的稳定性和速度，是深度学习发展史上的一个关键性创新。

八、代码实战------价格分类

8.1 工具包

import torch
from torchsummary import summary
from torch.utils.data import TensorDataset # 导入PyTorch的TensorDataset类，用于将数据封装成数据集
from torch.utils.data import DataLoader    # 导入PyTorch的DataLoader类，用于批量加载数据
import torch.nn as nn                      # 导入PyTorch的神经网络模块
import torch.optim as optim                # 导入PyTorch的优化器模块
from sklearn.datasets import make_regression # 导入sklearn生成回归数据集的函数
from sklearn.model_selection import train_test_split # 导入sklearn的数据集分割函数
import matplotlib.pyplot as plt            # 导入matplotlib绘图库
import numpy as np                         # 导入numpy数值计算库
import pandas as pd                        # 导入pandas数据分析库
import time                                # 导入时间处理模块

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

8.2 数据获取

8.2.1 读取数据

data = pd.read_csv('data\手机价格预测.csv')
x = data.iloc[:, :-1]
y = data.iloc[:, -1]

8.2.2 分割数据

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)

8.2.3 转换数据

x_train = torch.tensor(x_train.values, dtype=torch.float32)
x_test = torch.tensor(x_test.values, dtype=torch.float32)
y_train = torch.tensor(y_train.values, dtype=torch.int64)
y_test = torch.tensor(y_test.values, dtype=torch.int64)

8.2.4 封装tensor

train_dataset = TensorDataset(x_train, y_train)
test_dataset = TensorDataset(x_test, y_test)

8.2.5 创建数据加载器

train_loader = DataLoader(train_dataset, batch_size=8, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=8, shuffle=False)

8.3 模型构建

class model(nn.Module):
    # __init__ 初始化
    def __init__(self):
        super(model, self).__init__()
        self.layer1 = nn.Linear(in_features=20, out_features=64)
        self.layer2 = nn.Linear(in_features=64, out_features=128)
        self.layer3 = nn.Linear(in_features=128, out_features=4)
        self.dropout = nn.Dropout(p=0.9)

    # forward 前向传播
    def forward(self, x):
        x = self.layer1(x)
        x = self.dropout(x)
        x = torch.relu(x)
        x = self.layer2(x)
        x = self.dropout(x)
        x = torch.relu(x)
        out = self.layer3(x)

        return out

8.4 模型训练

def train():
    phone_model = model()
    # 损失函数
    criterion = nn.CrossEntropyLoss()
    # 优化器
    optimizer = optim.SGD(phone_model.parameters(), lr=0.1)
    # 遍历epoch
    epoches = 20
    for epoch in range(epoches):
        loss_sum = 0
        samples = 0
        for x, y in train_loader:
            # 前向传播
            y_pred = phone_model(x)
            # 计算损失
            loss = criterion(y_pred, y)
            # 梯度清零
            optimizer.zero_grad()
            # 反向传播
            loss.backward()
            # 参数更新
            optimizer.step()

            loss_sum += loss.item()
            samples += 1
        print(f"平均损失：{loss_sum/samples*1.0}")
    # 保存模型
    torch.save(phone_model.state_dict(), 'model/phone_model.pth')

8.5 模型测试

def test():
    my_model = model()
    my_model.load_state_dict(torch.load('model/phone_model.pth'))

    correct_sum = 0
    for x, y in test_loader:
        y_pred = my_model(x)
        y_index = torch.argmax(y_pred, dim=1)
        correct_sum += (y_index == y).sum()

    acc = correct_sum.item() / len(test_dataset)
    print(f"准确率：{acc*100.0}%")

8.6 模型实例化

if __name__ == '__main__':
    my_model = model()
    summary(my_model, input_size=(20,), batch_size=10, device='cpu')
    # train()
    test()

• 代码输出：

  ---

        Layer (type)               Output Shape         Param #

  ================================================================
  Linear-1 [10, 64] 1,344
  Dropout-2 [10, 64] 0
  Linear-3 [10, 128] 8,320
  Dropout-4 [10, 128] 0
  Linear-5 [10, 4] 516

  Total params: 10,180
  Trainable params: 10,180
  Non-trainable params: 0

  Input size (MB): 0.00
  Forward/backward pass size (MB): 0.03
  Params size (MB): 0.04
  Estimated Total Size (MB): 0.07

  D:\Desktop\Deep-learning\【DL 第一弹】\DAY03：【DL 第一弹】神经网络\14_手机价格分类\main.py:97: FutureWarning: You are using torch.load with weights_only=False (the current default value), which uses the default pickle module implicitly. It is possible to construct malicious pickle data which will execute arbitrary code during unpickling (See https://github.com/pytorch/pytorch/blob/main/SECURITY.md#untrusted-models for more details). In a future release, the default value for weights_only will be flipped to True. This limits the functions that could be executed during unpickling. Arbitrary objects will no longer be allowed to be loaded via this mode unless they are explicitly allowlisted by the user via torch.serialization.add_safe_globals. We recommend you start setting weights_only=True for any use case where you don't have full control of the loaded file. Please open an issue on GitHub for any issues related to this experimental feature.
  my_model.load_state_dict(torch.load('model/phone_model.pth'))
  准确率：27.0%