头歌Educator机器学习与数据挖掘-逻辑回归

答案分享

第1关：逻辑回归算法大体思想

复制代码

#encoding=utf8

import numpy as np

#sigmoid函数
def sigmoid(t):
    #输入：负无穷到正无穷的实数
    #输出：转换后的概率值
    result = 0
    #********** Begin **********#
    result = 1 / (1 + np.exp(-t))
    # 强制四舍五入到 12 位小数，以匹配最严格的测试用例精度
    result = np.round(result, 12) 
    #********** End **********#
    return result


if __name__ == '__main__':
    pass

第2关：逻辑回归的损失函数

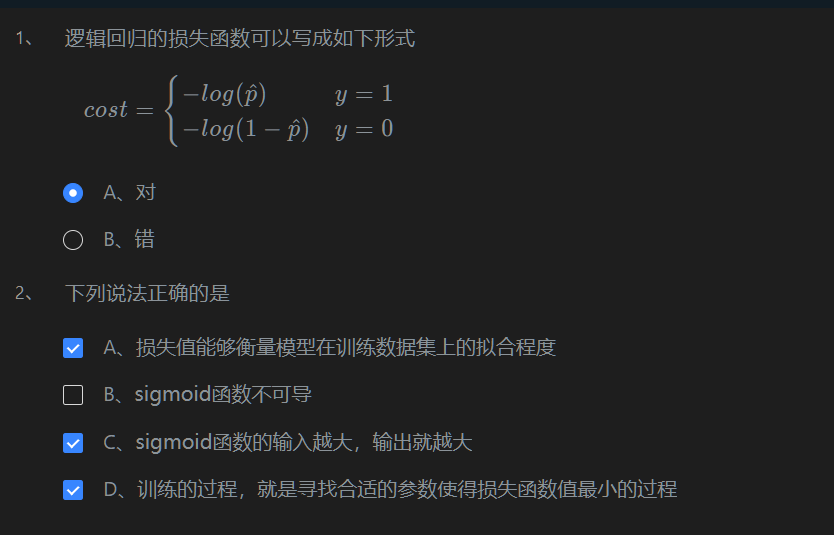
第3关：梯度下降

复制代码

# -*- coding: utf-8 -*-

import numpy as np
import warnings
warnings.filterwarnings("ignore")

#梯度下降,inital_theta为参数初始值，eta为学习率，n_iters为训练轮数，epslion为误差范围
def gradient_descent(initial_theta,eta=0.05,n_iters=1e3,epslion=1e-8):
    #  请在此添加实现代码  #
    #********** Begin *********#
    theta = initial_theta
    n_iters = int(n_iters)
    
    # 定义损失函数及其梯度
    def dJ(theta):
        # 梯度：2 * (theta - 3)
        return 2 * (theta - 3)

    # 迭代进行梯度下降
    for i in range(n_iters):
        gradient = dJ(theta)
        last_theta = theta
        
        # 更新参数：theta = theta - eta * gradient
        theta = theta - eta * gradient
        
        # 提前停止条件：如果参数变化小于epslion
        if(np.abs(theta - last_theta) < epslion):
            break

    #********** End **********#
    return theta

第4关：逻辑回归算法流程

复制代码

# -*- coding: utf-8 -*-

import numpy as np
import warnings
warnings.filterwarnings("ignore")
#定义sigmoid函数
def sigmoid(x):
    return 1/(1+np.exp(-x))

#梯度下降，x为输入数据，y为数据label，eta为学习率，n_iters为训练轮数
def fit(x,y,eta=1e-3,n_iters=1e4):
    #  请在此添加实现代码  #
    #********** Begin *********#
    m, n = x.shape
    
    # 1. 初始化参数 theta：维度为 (n, 1) 或 (n,)
    # 我们假设 x 已经是增广矩阵（包含 x0=1），theta 的长度应与特征数量 n 匹配
    theta = np.zeros(n) 
    
    # 2. 确保 y 是一维向量
    y = y.flatten()

    # 3. 迭代进行梯度下降
    for i in range(int(n_iters)):
        
        # 线性预测：z = X * theta (这里使用矩阵乘法或点乘)
        # 注意：np.dot(x, theta) 自动处理 (m, n) @ (n,) -> (m,)
        z = np.dot(x, theta)
        
        # Sigmoid激活：hat_p = sigmoid(z)
        hat_p = sigmoid(z)
        
        # 梯度计算：(1/m) * X.T @ (hat_p - y)
        # 误差项：(hat_p - y)
        error = hat_p - y 
        
        # 梯度：(X.T @ error) / m。注意：np.dot(x.T, error) 自动处理 (n, m) @ (m,) -> (n,)
        gradient = np.dot(x.T, error) / m
        
        # 参数更新：theta = theta - eta * gradient
        theta = theta - eta * gradient
        
    #********** End **********#
    return theta

第5关：sklearn中的逻辑回归

复制代码

#encoding=utf8
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
import numpy as np # 确保numpy可用，尽管在这里主要用到sklearn

def cancer_predict(train_sample, train_label, test_sample):
    '''
    优化后的代码：引入特征缩放（StandardScaler）以提高模型性能和收敛稳定性。
    '''
    
    #********* Begin *********#
    
    # 1. 定义管道：将数据标准化和模型训练连接起来
    # max_iter=500 是为了防止收敛警告，random_state=42 保证可复现性。
    model_pipeline = Pipeline([
        ('scaler', StandardScaler()),
        ('logreg', LogisticRegression(max_iter=500, random_state=42))
    ])
    
    # 2. 训练管道：训练时会先对训练集进行拟合并缩放，然后用缩放后的数据训练模型。
    model_pipeline.fit(train_sample, train_label)
    
    # 3. 预测并返回结果：预测时会自动对测试集进行缩放（使用训练集的统计信息）。
    return model_pipeline.predict(test_sample)

    #********* End *********#