要用梯度下降，对模型进行训练，代价函数最好是凸函数，这样用梯度下降优化的时候，可以找到全局最小值，在线性回归中，成本函数是，均方误差，计算预测值和真实值的差值的平方，然后取平均值，来衡量模型的效果，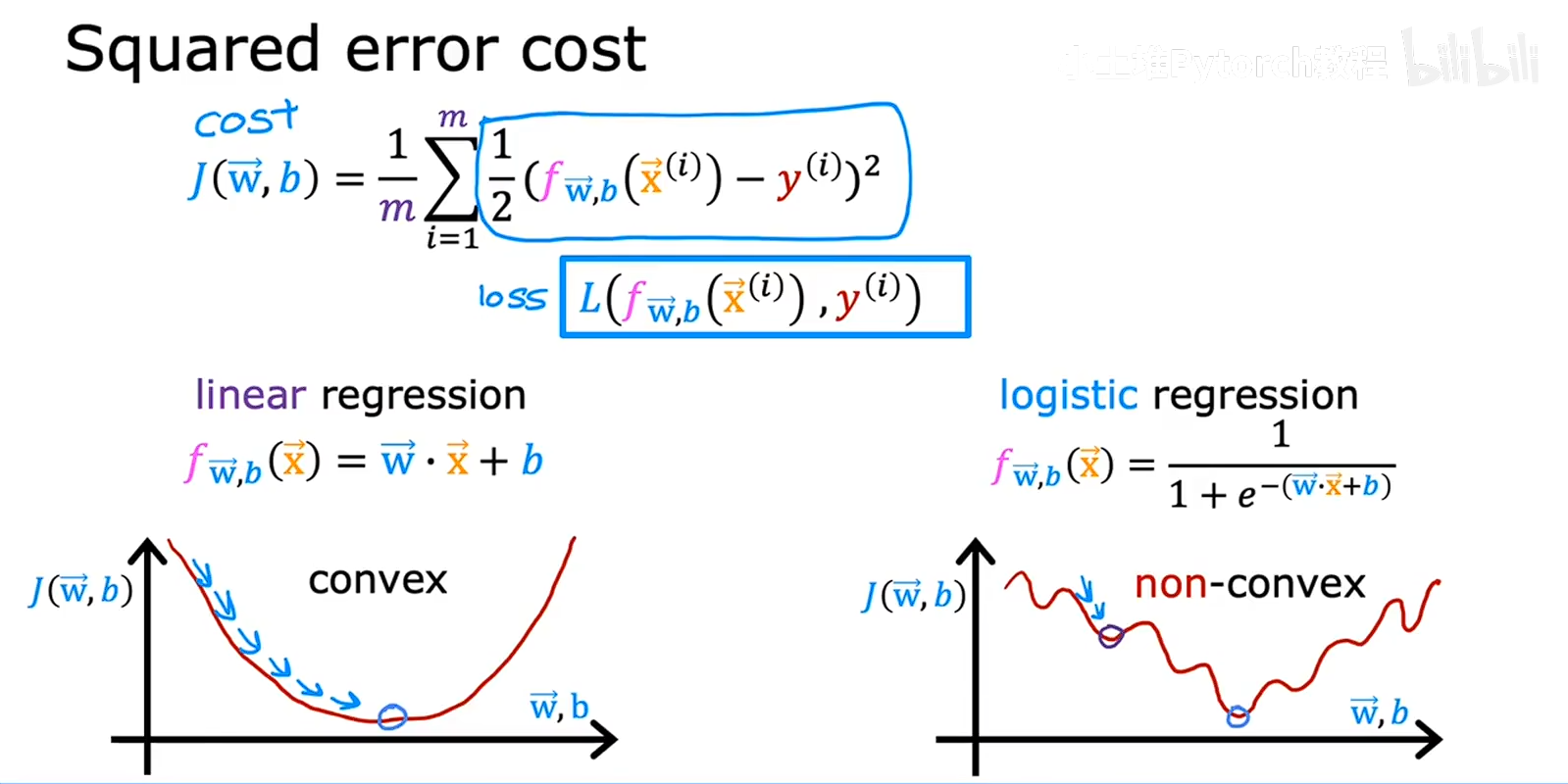
线性回归他是凸函数，可以好到全局最小值，但是逻辑回归则也用这个方法不行，逻辑回归处理的是分类问题，是0-1之间的概率，用均方误差会遇到局部最小值，如图所示，
所以我们要找到一个新的损失函数来定于逻辑回归的成本函数，如下图所示
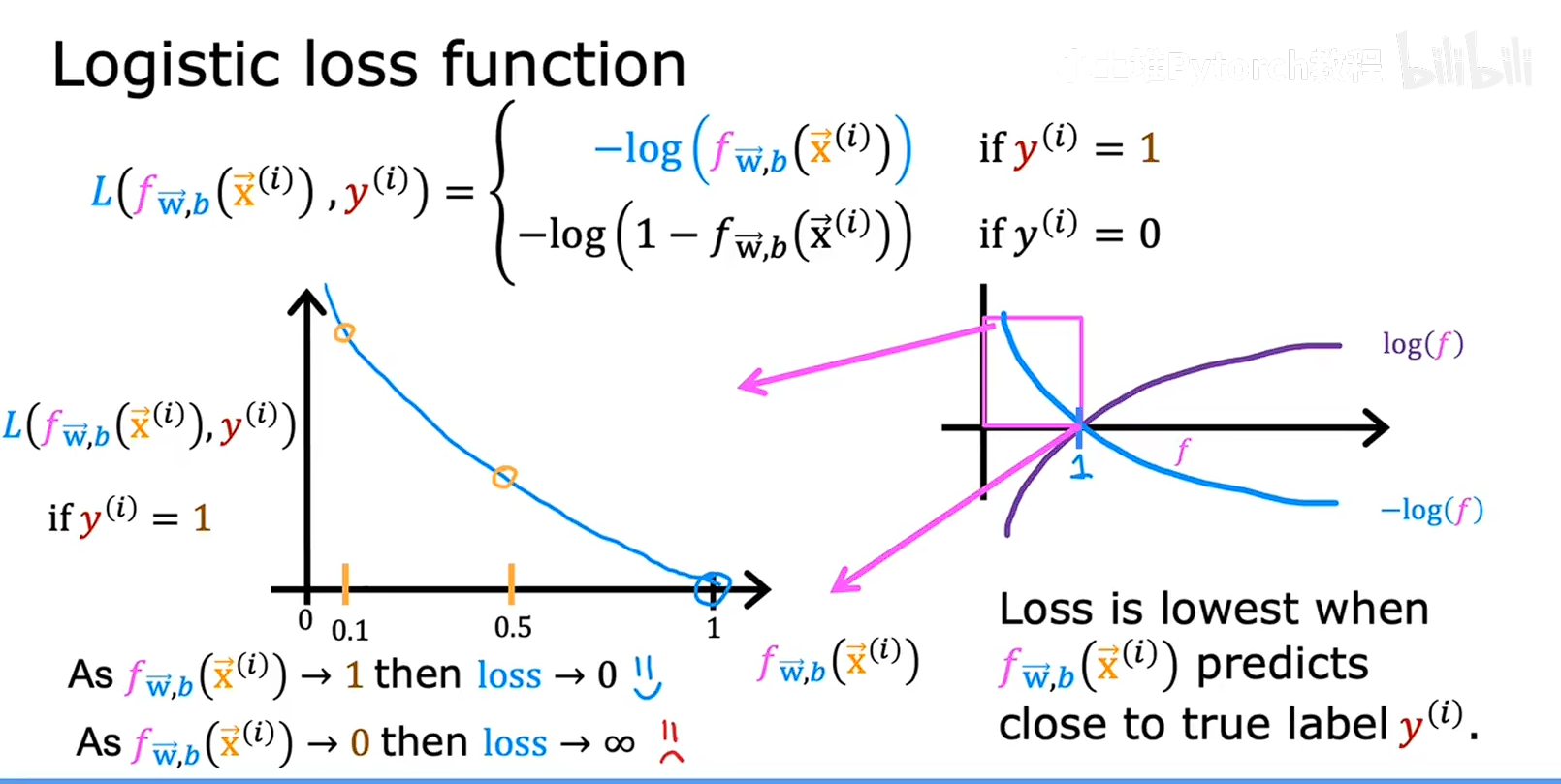
我们选择对数函数来做逻辑回归的成本函数，因为成本函数是一个给模型打分的一个函数，把模型的预测结果输入到成本函数中，成本函数给模型一个打分从而告诉模型准确程度，而逻辑回归是预测是一个概率，概率分布在0-1之间，我们设定一个阈值，这个阈值把0-1这个区间分成了两份，0-阈值，阈值-1，这个阈值就是决策边界，当概率落在第一个区间的时候，输出0，当概率落在第二个区间的时候，就输出1，所以当预测结果和真实结果不对的时候我们就要，惩罚模型，成本函数的输出就要大，例如，当我们要输出的是1但是模型预测的概率的是0.1，我们要告诉模型，0.1的概率不对，就要变大成本函数，所以，就要有一个函数，等于1的时候不要成本，不惩罚，与1偏差越大，惩罚成本就越高，刚好 对数函数 log就符合这个情况，而且还是凸函数，可以进行梯度下降，进行模型训练。
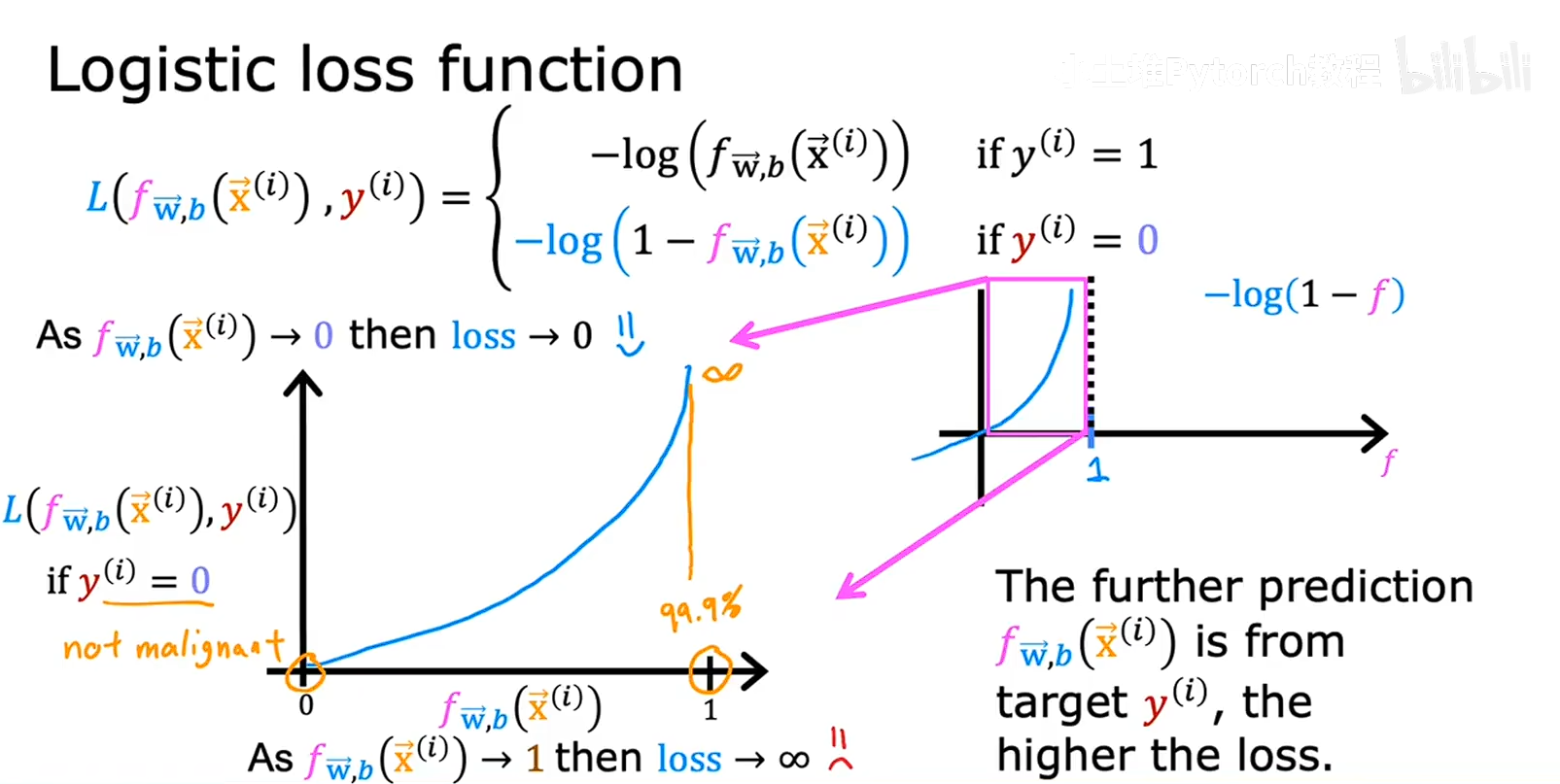
所以我们只关注对数函数 横轴0-1的部分，因为我们模型0要输出两种情况，0-1，所以要分情况去定义成本函数，1是一种情况，0是一种情况，在用代码实现的时候，也要对数据集的输出结果进行区分然后再带入模型进行训练，
下面是输出为0的时候的成本函数
