1、从感知机到神经网络的演进
1.1 感知机回顾与局限性
在学习神经网络之前,我们需要先回顾一下感知机(特指单层感知机)的基本概念。感知机是神经网络的基础,它模拟了生物神经元的信息处理过程。感知机接收多个输入信号,对这些信号进行加权求和,并与一个阈值进行比较,最终输出 0 或 1 的结果。
感知机的数学表达式为:y = f(∑wixi + b) ,其中 xi 是输入信号,wi是权重,b 是偏置,f 是激活函数(阶跃函数)。在第一章中我们已经了解到,感知机能够实现与门、与非门、或门等简单逻辑电路,但无法实现异或门这样的非线性问题。
感知机的局限性在于它只能处理线性可分的问题。这是因为感知机本质上是在寻找一个超平面来分隔不同类别的数据点。当数据不是线性可分的时候,感知机就无法找到这样的超平面,也就无法正确分类。
1.2 神经网络的引入
为了突破感知机的线性限制,我们引入了神经网络的概念。神经网络通过在输入层和输出层之间添加一个或多个隐藏层,形成多层结构,并在隐藏层中使用非线性激活函数,从而获得了处理非线性问题的能力。
神经网络与感知机的关键区别在于:
1)神经网络具有多层结构,包含输入层、隐藏层和输出层
2)隐藏层使用非线性激活函数(如 sigmoid 函数)
3)可以通过调整各层的权重和偏置来学习复杂的非线性关系
"多层感知机"(Multilayer Perceptron, MLP) 是指使用 sigmoid 函数等平滑激活函数的多层网络,这正是我们所说的神经网络。
2、神经网络中使用的典型激活函数
2.1 激活函数的必要性
激活函数是神经网络中非常重要的组成部分,它为神经网络引入了非线性变换能力。如果不使用激活函数,那么无论神经网络有多少层,其输出都将是输入的线性组合,这与单层感知机没有本质区别。
这种线性限制使得网络无法拟合数据中的非线性关系。例如,异或(XOR)问题就无法用纯线性模型解决。现实世界中的数据通常具有高度的非线性特征,如图像中的物体边界、语音信号的频谱特征、文本中的语义关系等,都需要非线性模型才能有效处理。
激活函数的引入使神经网络能够学习复杂的非线性映射关系。通过激活函数的非线性变换,即使是简单的两层神经网络也能够逼近任何连续函数,这就是著名的通用近似定理
激活函数的作用可以总结为以下几点:
1)引入非线性,使神经网络能够学习复杂的非线性关系
2)将神经元的输出限制在一定范围内(如 0-1 或 - 1 到 1)
3)决定神经元的激活状态,模拟生物神经元的阈值激活特性
2.2激活函数的基本要求
理想的激活函数应具备以下特性:
1) 非线性
激活函数必须是非线性的,否则多层网络将失去深度学习的意义。当激活函数为非线性时,两层神经网络就可以逼近基本上所有的函数。
2) 可微性
激活函数需要是可微的(允许在少数点不可导),因为神经网络的训练通常使用基于梯度的优化方法(如梯度下降),需要计算梯度来更新参数。
3) 梯度特性
激活函数的梯度不应过快趋近于零(梯度消失)或过大(梯度爆炸),以保证深层网络的稳定训练。梯度的范围需要在合适区间内,确保训练的效率和稳定性。
4) 计算效率
激活函数及其导数需要计算简单,因为激活函数在训练和推理过程中需要频繁计算,计算复杂度会直接影响网络的训练和推理速度。
5) 参数简洁性
激活函数应尽量不引入额外参数,避免增加模型复杂度。但现代一些激活函数如 PReLU、SELU 等通过引入可学习参数来提升性能,这是一个权衡问题。
2.3典型激活函数
2.3.1 Sigmoid 函数
Sigmoid 函数是神经网络中最早使用的激活函数之一,它的数学表达式为:
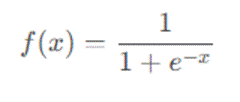
Sigmoid 函数具有以下特点:
1)输出范围在 (0,1) 之间,可以解释为概率
2)是一个平滑的函数,不同于阶跃函数的跳跃式变化
3)具有很好的对称性,关于点 (0,0.5) 对称
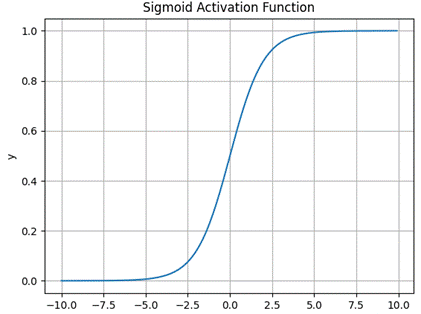
图 1Sigmoid 函数图像
2.3.2 Tanh 函数
Tanh(双曲正切)函数可以看作是 Sigmoid 函数的改进版本,其数学表达式为:
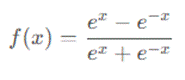
Tanh 函数将输入压缩到 (-1,1) 区间内,实现了零中心输出。这种零中心特性解决了 Sigmoid 函数的非零中心问题,在实际应用中通常表现更好
anh 函数相比 Sigmoid 的改进包括:
1) 零中心输出:输出以 0 为中心,有利于权重更新.
2) 梯度更强:在输入接近零的区域,Tanh 函数的梯度比 Sigmoid 函数更大,有助于加快学习速度
3) 对称性:函数关于原点对称,具有更好的数学性质
但 Tanh 函数仍然存在梯度消失问题,虽然比 Sigmoid 有所改善,但在深层网络中仍然是一个严重问题 。
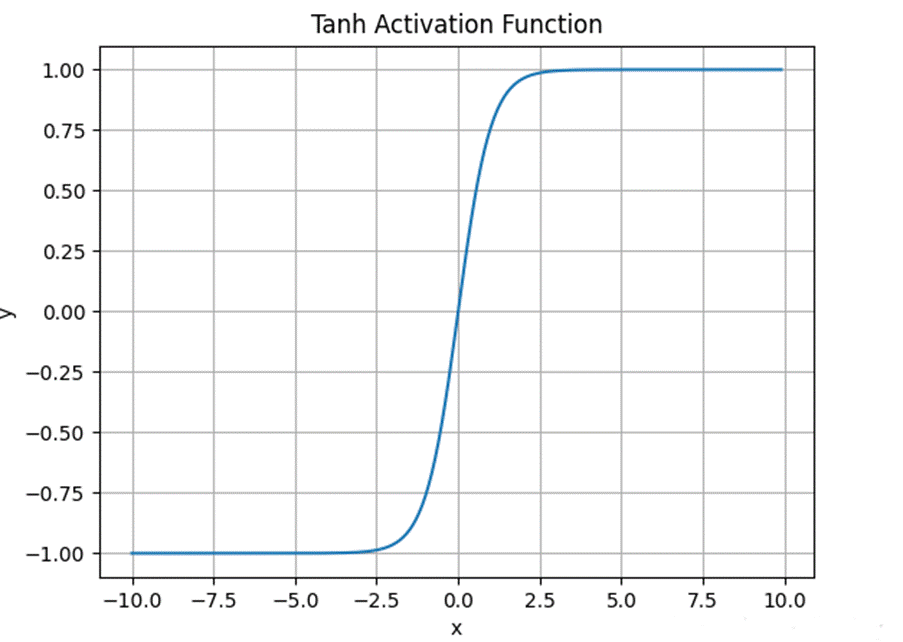
图 2Tanh函数图像
2.3.3 ReLU 函数
ReLU(Rectified Linear Unit,修正线性单元)是当前深度学习中最常用的激活函数之一,它的数学表达式为:
f(x) = max(0, x)
ReLU 函数具有以下特点:
1)当输入大于 0 时,直接输出该值;当输入小于等于 0 时,输出 0
2)计算简单,效率高
3)能够有效缓解梯度消失问题
4) 神经元死亡问题:当输入为负时,梯度为 0,可能导致某些神经元永远无法被激活,称为 "死亡神经元"
5) 输出非零中心:输出值恒为正,可能影响收敛速度
ReLU 函数的图像是一条折线,在 x=0 处有一个拐点。当输入为正时,输出等于输入;当输入为负时,输出为 0。这种简单的非线性特性使得 ReLU 在深层神经网络中表现出色。
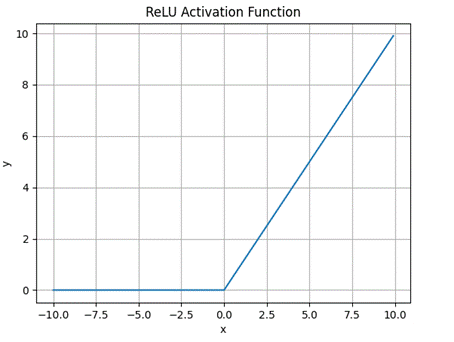
图 3 ReLU 函数图像
2.3.4 Leaky ReLU 函数
Leaky ReLU 是为了解决 ReLU 的 "死亡神经元" 问题而提出的改进版本。其数学表达式为:
LeakyReLU(x) = max(αx, x)
其中 α 是一个小的常数(通常取 0.01 或 0.02)。Leaky ReLU 在负值区域引入了一个小的斜率,使得负值输入也能产生一定的输出,从而避免神经元死亡。
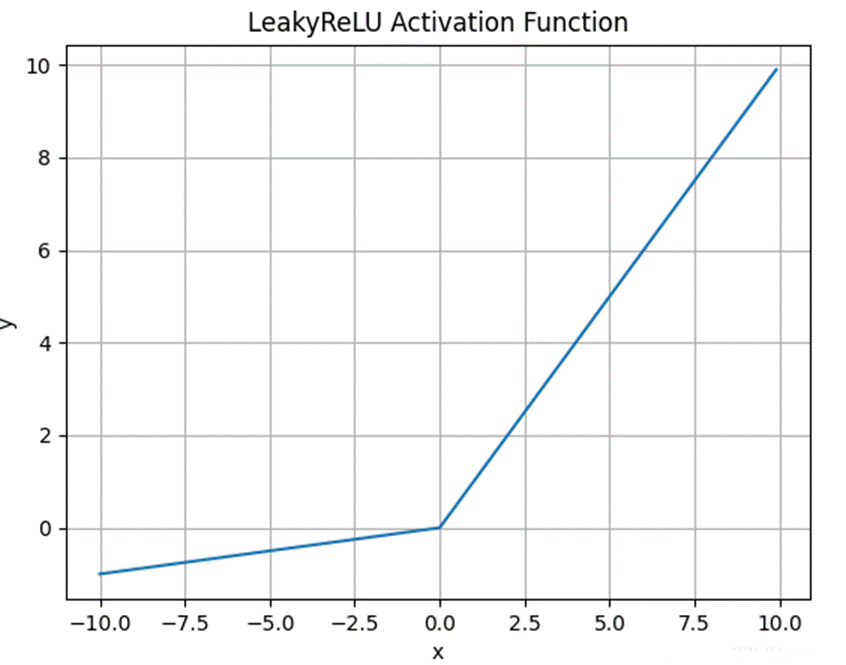
图 4 Leaky ReLU 函数图像
2.3.5 PReLU 函数
PReLU(Parametric ReLU,参数化 ReLU)是 Leaky ReLU 的进一步改进,它将 α 作为可学习的参数,在训练过程中与网络其他参数一起更新
PRelu激活函数的数学表达式为:
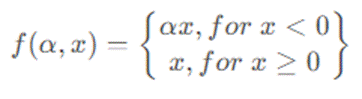
PReLU 的数学表达式与 Leaky ReLU 相同,但 α 不再是固定值,而是一个可学习的参数。这种设计使得网络能够自动学习最优的负值斜率。
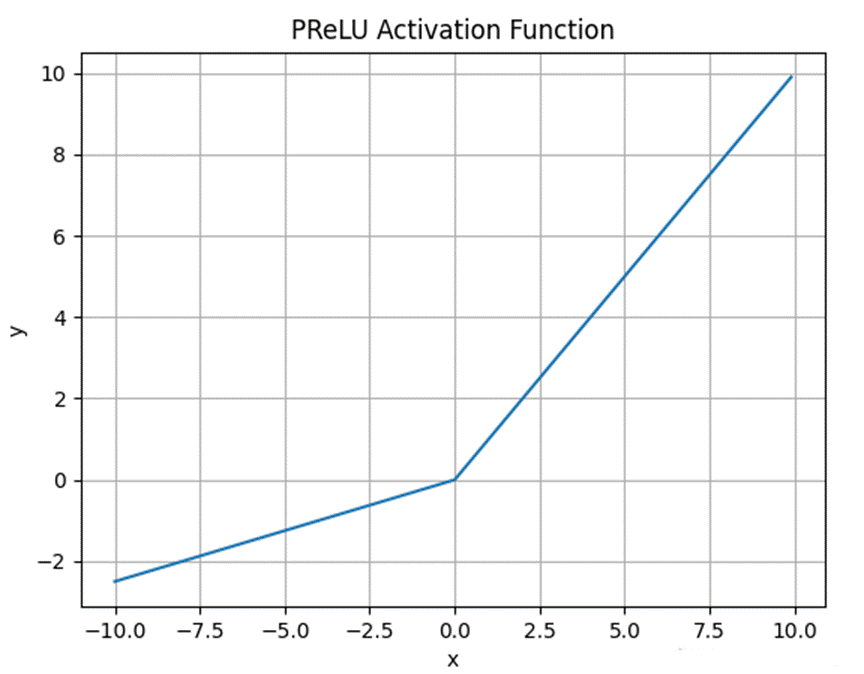
图 5 PReLU 函数图像
2.3.6 RReLU 函数
RReLU(Random ReLU)是另一种 Leaky ReLU 的变体,其中 α 在训练时从高斯分布中随机采样,在测试时固定为一个平均值
RReLU 的数学表达式与 Leaky ReLU 相同,但 α 是随机的。这种随机性可以看作是一种正则化技术,有助于防止过拟合。
2.3.7 ELU函数
ELU(Exponential Linear Unit,指数线性单元)是一种更复杂的 ReLU 变体,由 Djork 等人提出。其数学表达式为:
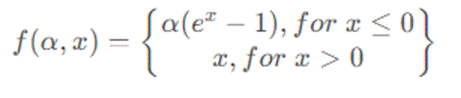
其中 α 是一个超参数,通常设为 1 。ELU 在负值区域使用指数函数,使其具有更好的噪声鲁棒性,同时能够使神经元的平均激活值趋近于 0。
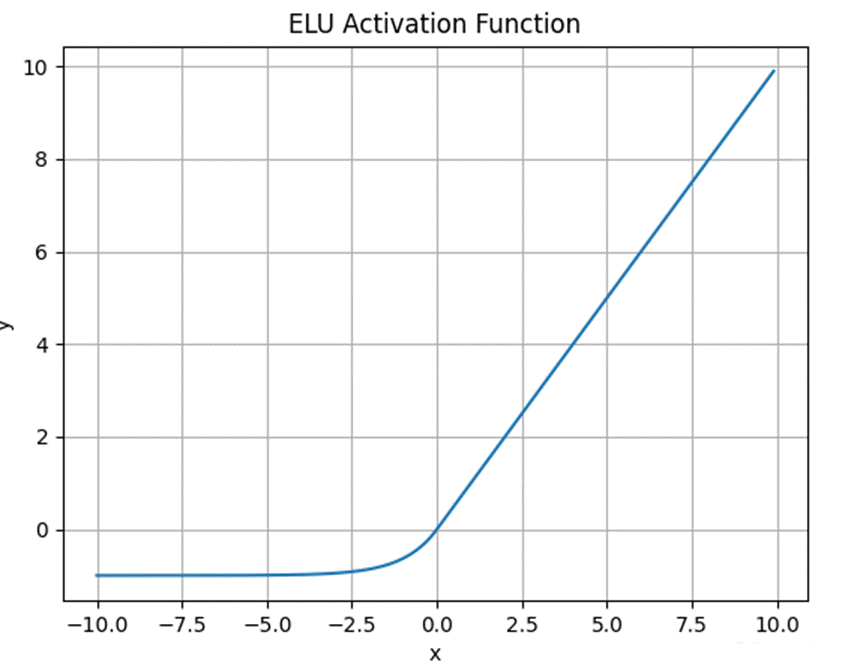
图 6ELU 函数图像
2.3.8 SELU 函数
SELU(Scaled ELU,缩放指数线性单元)是 ELU 的自归一化版本,通过固定缩放参数 λ 和形状参数 α,使网络具备自归一化特性 。
SELU 的数学表达式为:
SELU(x) = λ · ELU(x)
其中 α=1.67326,λ=1.0507,这些值是通过论文优化得到的 。当配合特定的初始化方法(如 LeCun 正态初始化)时,SELU 能够使每一层的输入保持零均值和单位方差,大幅简化超参数调优。
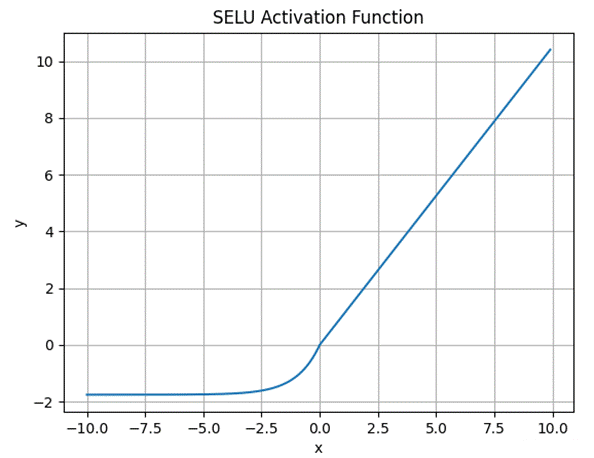
图 7 SELU 函数的图像
2.3.9Swish 函数
Swish 函数由 Google Brain 团队在 2017 年提出,其设计灵感来自于对神经网络中复杂模式的观察。Swish 函数的独特之处在于它结合了线性和非线性的特性 。
Swish 函数的数学表达式为:
Swish(x) = x · σ(βx) = x/(1+e^(-βx))
其中 β 是一个常数或可训练的参数。当 β=0 时,Swish 变为线性函数 f (x)=x/2;当 β→∞时,Swish 变为 ReLU 函数。因此,Swish 可以看作是介于线性函数与 ReLU 函数之间的平滑函数 。
Swish 具备无上界有下界、平滑、非单调的特性。在深层模型上的效果优于 ReLU,例如在 ImageNet 分类任务上,使用 Swish 的模型比使用 ReLU 的模型获得了更高的准确率 。
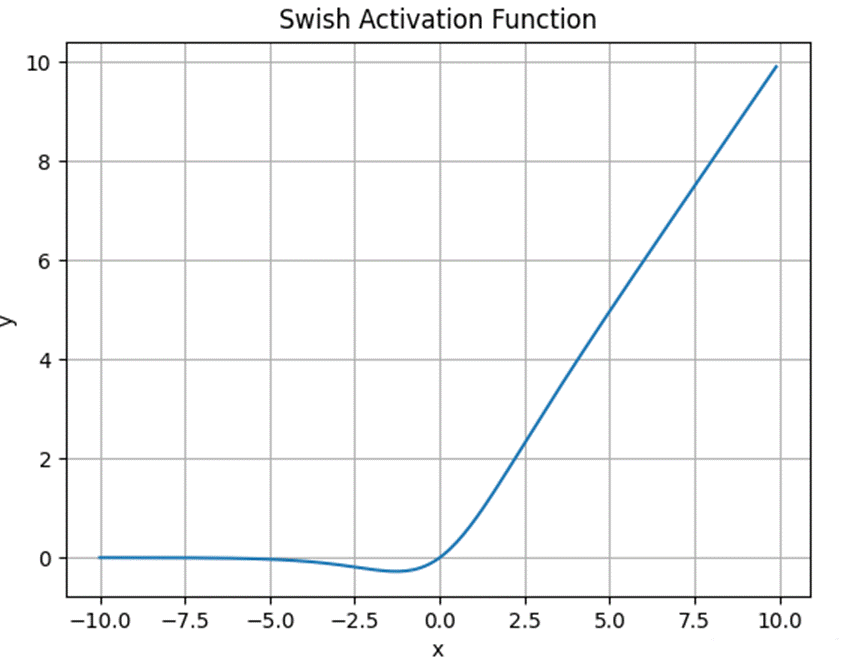
图 8Swish 函数图像
2.3.10 GELU 函数
GELU(Gaussian Error Linear Unit,高斯误差线性单元)是另一个引起广泛关注的新型激活函数,在 Transformer 模型中得到了广泛应用。
GELU 的数学表达式为:
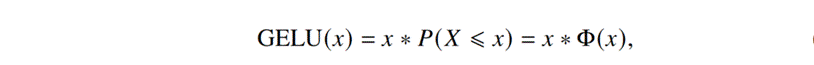
其中 Φ(x) 是标准正态分布的累积分布函数。GELU 函数的设计灵感来自于一个有趣的想法:如果将输入值视为一个随机变量,那么激活函数可以被看作是一种智能的 "门控" 机制,决定是否让这个输入通过。
GELU 可以被近似的表示为:
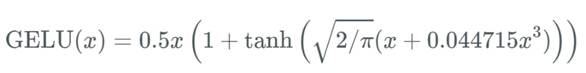
或者:
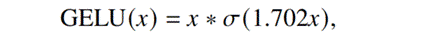
其中:σ()代表Sigmoid函数。
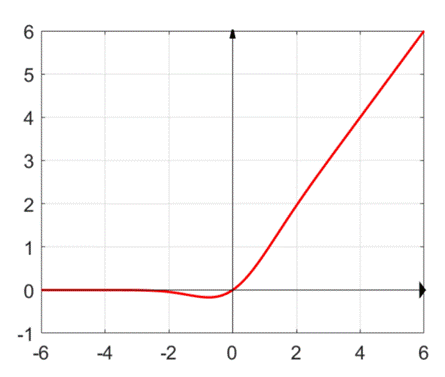
图 9 GELU 函数图像