一、递归算法
前序遍历:
后续遍历:
中序遍历:
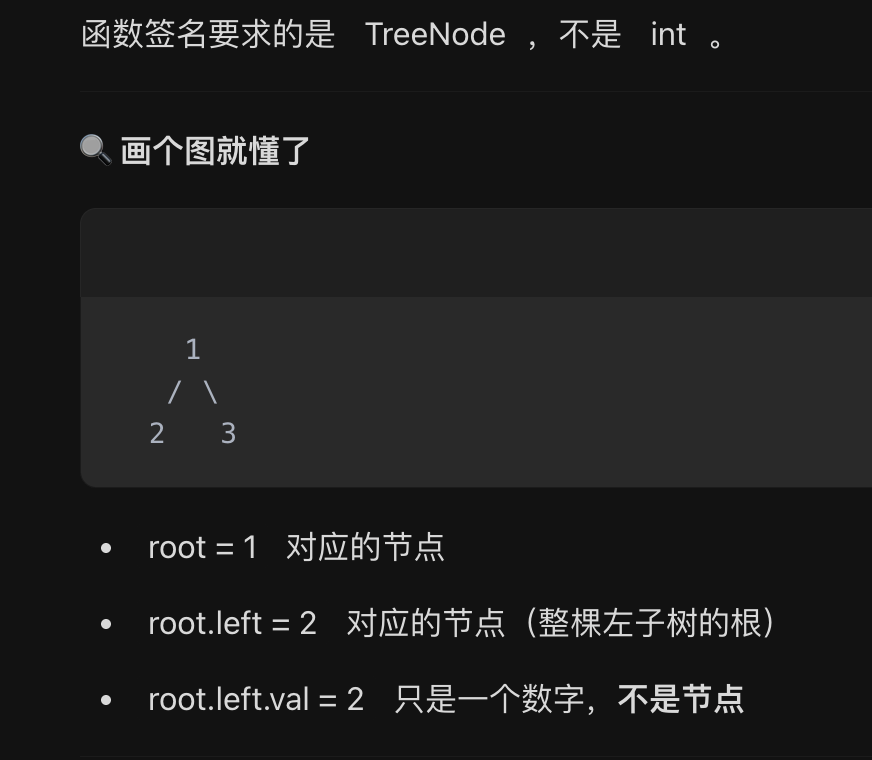
1、为什么是self.Traversal(root.right) 为什么不是self.Traversal(root.right.val)呢
递归函数要的是"子树根节点",不是"子树根节点的值"。
值只是用来拼结果列表的,递归还得靠节点本身。
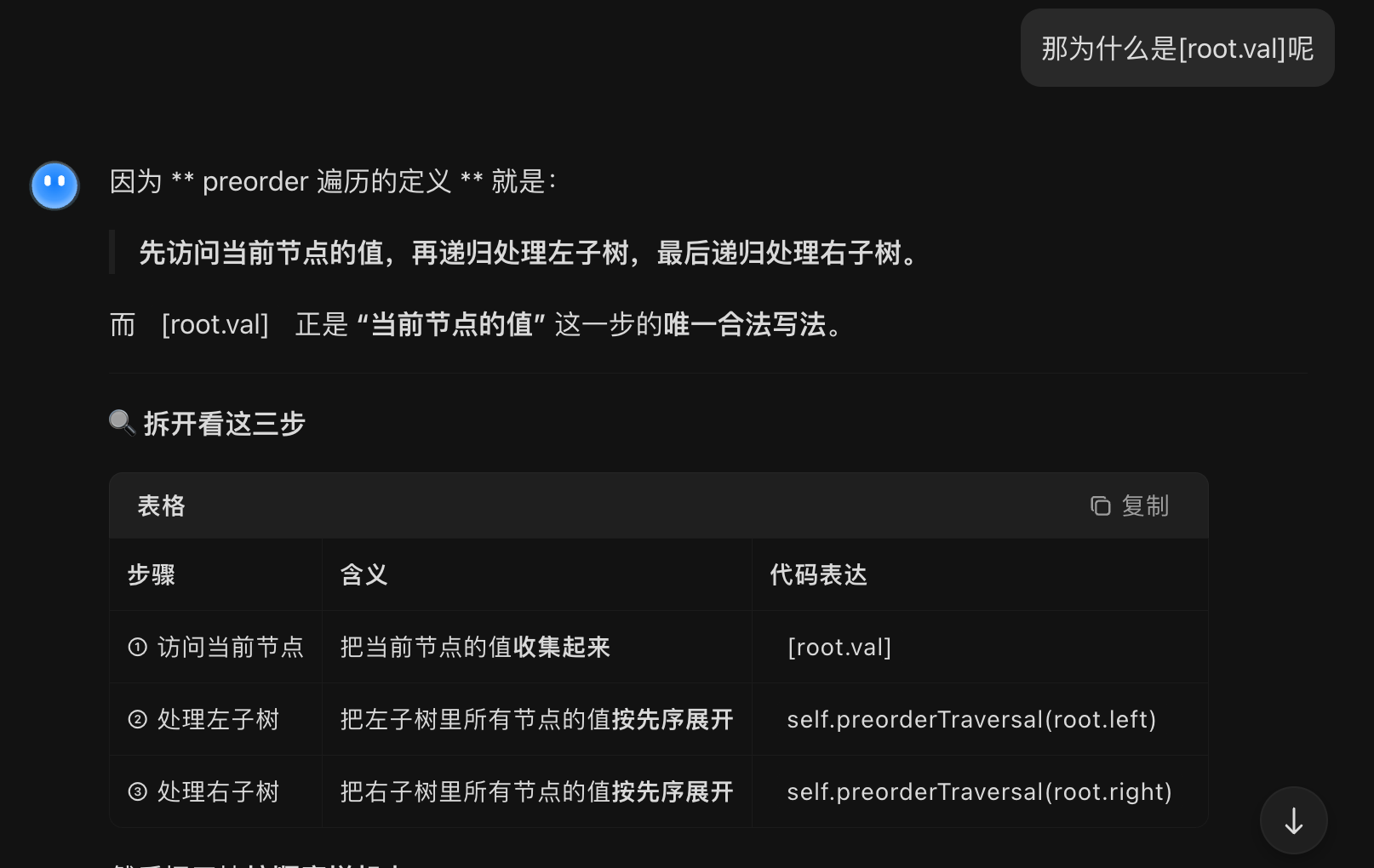
2、那为什么是[root.val]呢
二、层序遍历算法
层序遍历就是一层一层遍历节点
python
from collections import deque
from typing import Optional, List
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if root is None:
return []
q = deque([root])
ans = [] # 总答案
while q:
sz = len(q)
level = [] # 当前层结果
for _ in range(sz):
cur = q.popleft()
level.append(cur.val) # 收集值
if cur.left:
q.append(cur.left)
if cur.right:
q.append(cur.right)
ans.append(level) # 把整层放进答案
return ans详细解释
python
from collections import deque
#引入双端队列,因为后面需要 O(1) 时间 从头部弹出元素;列表 pop(0) 是 O(n)。
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
#定义函数,输入是 二叉树根节点,输出是 List[List[int]]
#外层列表代表"层",内层列表代表"该层从左到右的所有节点值"。
if root is None:
return []
#空树直接返回空列表,避免后面出现 q.popleft() 对空队列操作。
q = deque([root])
#初始化队列,把根节点放进去。此时队列里只有 1 个元素,即第 0 层(第一层)的起点。
ans = []
#总答案,将来要返回 [[3], [9,20], [15,7]] 这种格式。
while q:
#外层循环:只要队列里还有节点,就说明 尚未遍历完整个树。
sz = len(q)
#关键:在进入内层循环之前,先记录 当前队列长度。
#这个长度就是 当前层的节点个数,因为上一轮的循环已经把下一层所有节点都塞进队列了。
level = []
#新建一个空列表,用来收集 本层所有节点的值。
for _ in range(sz):
#内层循环 恰好执行 sz 次,保证 只处理当前层,不会动到下一层节点。用 _ 表示循环变量本身不会被用到。
cur = q.popleft()
#取出队列 最左边 的节点(FIFO)。它一定是当前层 从左往右 的下一个节点。
level.append(cur.val)
#把该节点的 值 放进本层列表,注意 不是节点本身,而是 val。
if cur.left: q.append(cur.left)
if cur.right: q.append(cur.right)
#只要该节点有左/右孩子,就把孩子 追加到队列尾部。
#这些孩子的 深度比当前层大 1,因此 不会在本次内层循环里被处理,留到下一轮 while 再说。
ans.append(level)
#内层循环结束,本层所有值已收集完,把 level 塞进总答案。
#此时队列里只剩 下一层所有节点,下次 while 继续。
return ans
#整棵树层序完成,返回 [[layer1], [layer2], ...]。2、最小深度算法
原题:https://leetcode.cn/problems/minimum-depth-of-binary-tree/submissions/669301070/
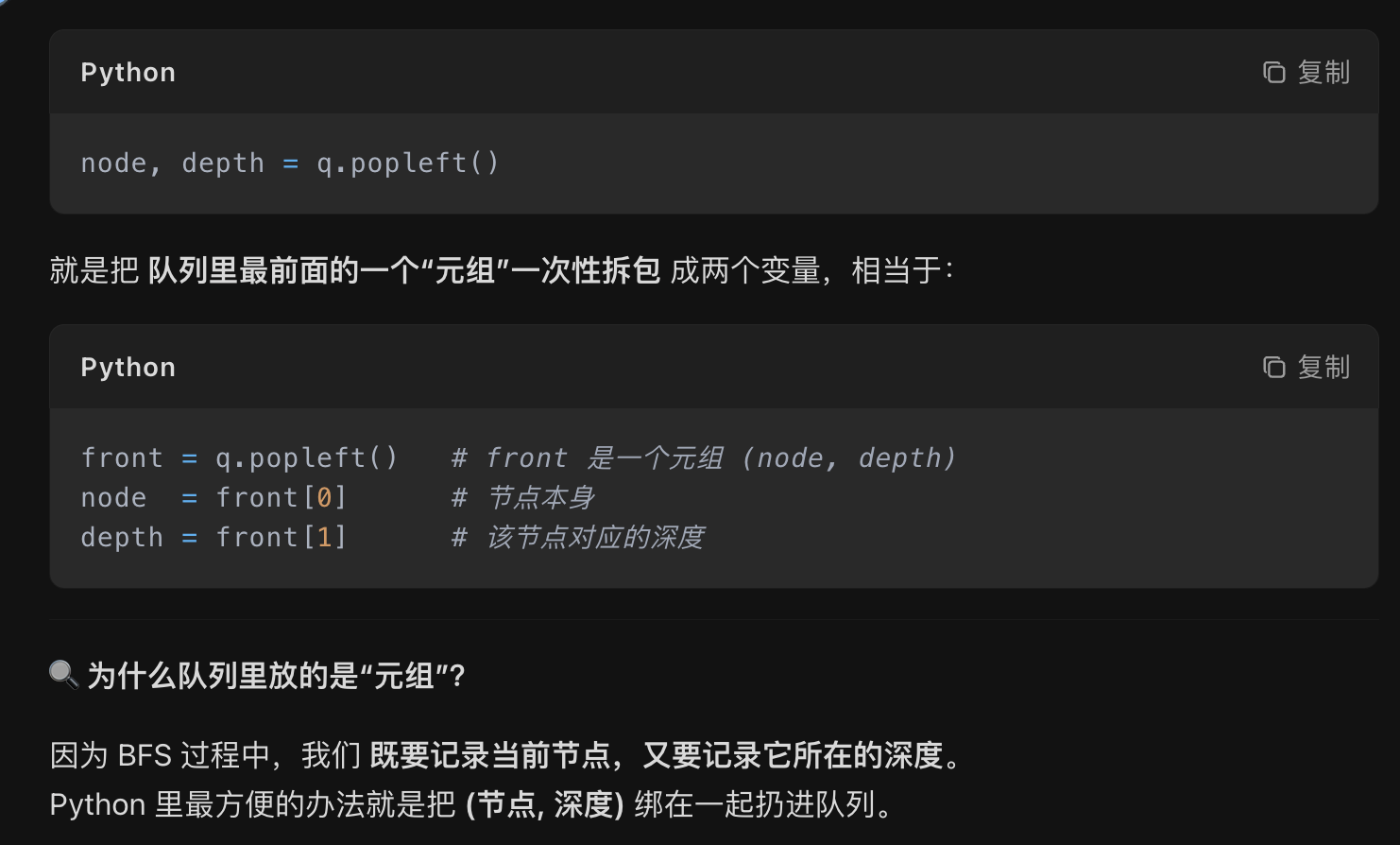
node, depth = q.popleft() 就是 一次性从队列里取出"节点"和"它对应的深度",省得再写两行赋值。相当于下面这个:
front = q.popleft() # front 是一个元组 (node, depth)
node = front[0] # 节点本身
depth = front[1] # 该节点对应的深度
python
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
if root is None:
return 0
q = deque([(root,1)])
while q:
node,depth = q.popleft()
if not node.left and not node.right:
return depth
if node.left:
q.append((node.left,depth + 1))
if node.right:
q.append((node.right,depth + 1))